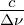 .
.

| Literatur | |
Wir betrachten Wellen, die sich auf verschiedenen Wegen ausbreiten und die unterschiedliche Abstände zu einer Quelle haben.
| Zwei Wellen heissen kohärent, wenn sie, bis auf eine Phase, die gleiche Zeitabhängigkeit haben. |
| Versuch zur Vorlesung: | |
| Kohärenz (Versuchskarte O-051) | |
Die Kohärenz von Wellen ist nur im Idealfall überall und zu jeder Zeit gegeben.
Hat eine Quelle (ein gedämpfter harmonischer Oszillator)
eine Bandbreite Δν, dann ist die Kohärenzzeit τ ≈ Δν−1 und
L ≈cτ ≈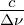 .
.
Ist die Lichtquelle ausgedehnt (Breite b), dann gibt es nur
im Winkelbereich σ < 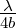 eine kohärente Überlagerung.
eine kohärente Überlagerung.
Die Intensität muss verschieden berechnet werden, je
nachdem ob die beiden Wellenzüge mit den Amplituden 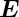 1
und
1
und 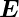 2 kohärent oder nicht sind.
2 kohärent oder nicht sind.
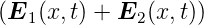 2
2
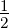
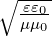
![2 2
[E1(x, t) + E2 (x,t) ]](op-2016-2017186x.png)
Bei kohärenten Wellen mit dem Phasenunterschied ϕ
und den Amplituden 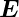 1 und
1 und 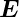 2 ist die resultierende
Amplitude
2 ist die resultierende
Amplitude
| Literatur | |
Wenn wir eine nach links laufende Welle A1(x,t) = A0 exp 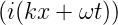 und eine nach rechts laufende Welle A2 = A0 exp
und eine nach rechts laufende Welle A2 = A0 exp 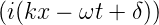 mit gleicher Amplitude zur Interferenz kommen lassen,
erhalten wir
mit gleicher Amplitude zur Interferenz kommen lassen,
erhalten wir
Die Summe der beiden Wellenfunktionen ist das Produkt zweier Terme
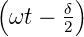
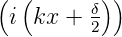
Damit bilden sich räumlich stehende Knotenlinien aus, wir haben eine stehende Welle.
| Stehende Wellen als Resultat zweier gegenläufiger Wellen gibt es in jedem Resonator, insbesondere in Laserresonatoren. |
| Literatur | |
In Gleichung (3.2) zeigt sich, dass bei einem optischen Aufbau, der effektiv nur von einer Ortskoordinate abhängt, die zeitlich gemittelte Amplitude nur von der Phase δ abhängt. Das heisst, dass es reicht, die Phasen zu untersuchen! Beachten Sie, in Gleichung (3.2) wurde die Phase δ nur einem Weg zugeordnet, die zeitgemittelte Amplitude hängt aber von cos(δ∕2) ab.
__________________________________________________________________________
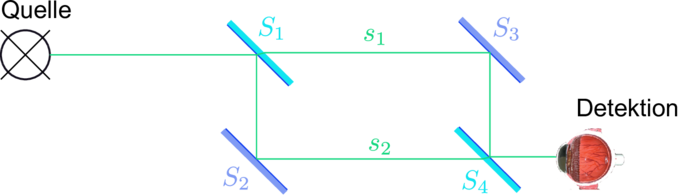
Aufbau des Mach-Zehnder-Interferometers.
_____________________________________________________________________
Abbildung 3.2.2 zeigt den schematischen Aufbau eines Mach-Zehnder-Interferometers. Licht aus der Quelle trifft auf den halbdurchlässigen Spiegel S1 und spaltet sich in die zwei Wege s1 und s2 auf. Der Weg s1 läuft vom Spiegel S1 über S3 nach S4, der Weg s2 vom Spiegel S1 über S2 nach S4. Am Spiegel S4 werden die Lichtwellen vereinigt und gelangen interferierend auf den Detektor.
Die relative Phase des Lichtes für die beiden Wege s1 und s2 kann aus dem Brechungsindexverlauf entlang der Wege berechnet werden. Die Geschwindigkeit ist durch c(s) = c0∕n(s) gegeben. Dann ist
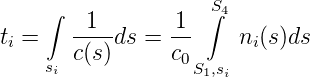 | (3.3) |
Die Phasendifferenz von Licht mit der Vakuumwellenlänge λ0 und damit der Frequenz ω = 2πν = 2πc0∕λ0 ist
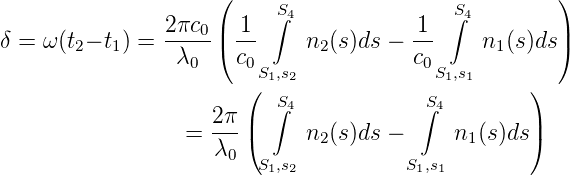 | (3.4) |
Die beobachtete zeitgemittelte Amplitude am Ort x = 0
(kann willkürlich gewählt werden!) ist nach Gleichung
(3.2) mit  (δ) =
(δ) = 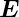 1(x,t) +
1(x,t) + 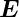 2(x,t), beide mit gleichen
Amplituden
2(x,t), beide mit gleichen
Amplituden 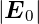
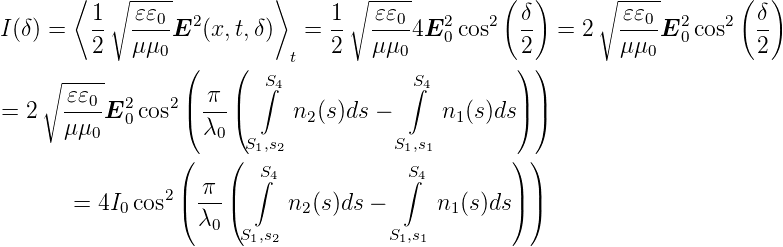 | (3.5) |
wobei I0 = 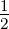
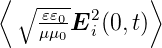 t =
t = 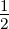
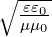
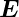 02 ist.
02 ist.
Das heisst, dass das Ausgangssignal des Mach-Zehnder-Interferometers nicht nur von der geometrischen Weglängendifferenz, sondern auch von Unterschieden der Brechungsindizes abhängt. Das Licht läuft in beiden Armen mit einer definierten Richtung. Das heisst, dass der Ausgang des Mach-Zehnder-Interferometers abhängig zum Beispiel von der Fliessrichtung eines Mediums mit dem Brechungsindex n ist. Mach-Zehnder-Interferometer werden kaum zur Distanzmessung aber oftmals zur Messung von Brechungsindexdifferenzen verwendet.
| Literatur | |
| Versuch zur Vorlesung: | |
| Michelson-Interferometer (Versuchskarte O-031) | |
_______________________________________________
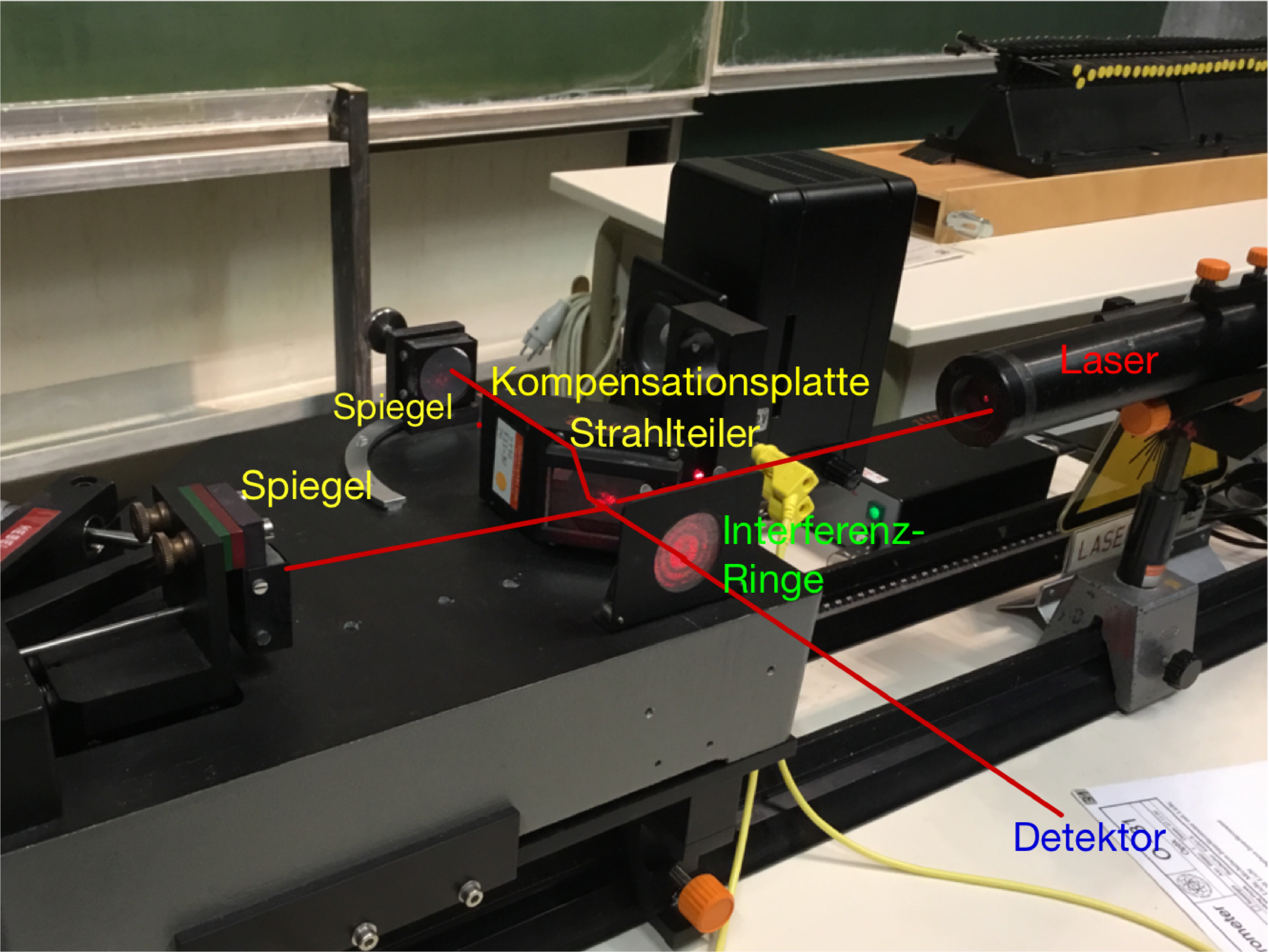
Bild des Michelson-Interferometers aus der Vorlesungssammlung mit eingezeichnetem Strahlengang.
_____________________________________________________________________
_____________________________________________________________________
Schematische Zeichnung des Aufbaus eines Michelson-Interferometers aus Abb. 3.2.3.
_____________________________________________________________________
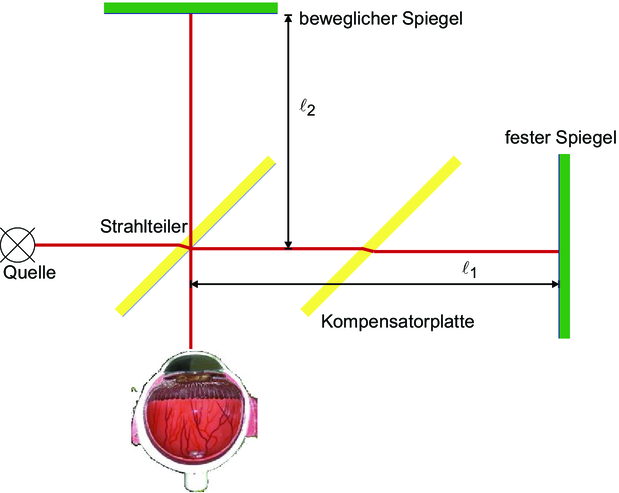
Beim Michelson-Interferometer wird Licht durch einen Strahlteiler in zwei Lichtwege aufgespalten. Der Weg vom Strahlteiler zum festen Spiegel sei ℓ1, der zum beweglichen ℓ2. Analog zum Mach-Zehnder-Interferometer (siehe Abschnitt 3.2.2) kann die Phase wie folgt geschrieben werden:
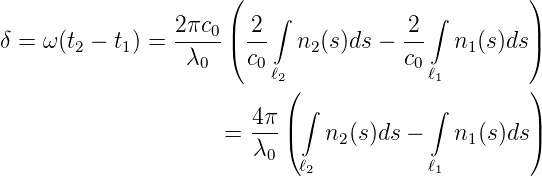 | (3.6) |
Die Phase hängt also sowohl vom Weglängenunterschied wie auch von Unterschieden im Brechungsindex ab. Anders als beim Mach-Zehnder-Interferometer wird jeder Weg zweimal und zwar gegenläufig durchlaufen. Bewegungseffekte mitteln sich so in erster Näherung heraus.
Der gesamte Weglängenunterschied ist bei konstantem ni(s) = n0 durch Δℓ = 2(ℓ2 −ℓ1) gegeben. Immer wenn Δℓ ein ganzzahliges Vielfaches der Wellenlänge λ ist, tritt konstruktive Interferenz auf. Wird der bewegliche Spiegel um λ∕4 verschoben, ändert sich Δℓ um λ∕2, dann haben wir destruktive Interferenz.
Wenn wir das Interferometer am Ausgang mit einer Intensität von I0 betreiben und wenn wir eine Intensitätsänderung von ΔI noch messen können, dann können wir die mögliche Distanzauflösung in nichtmagnetischen Medien wie folgt berechnen:
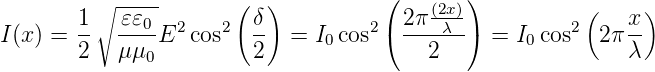 | (3.7) |
oder umgeschrieben
![I0 [ ( x-)]
I(x) = 2 1 + cos 4 πλ](op-2016-2017209x.png) | (3.8) |
Die Ableitung dieser Gleichung ist
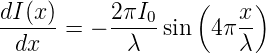 | (3.9) |
Die maximale Steigung, also die höchste Empfindlichkeit beträgt
 | (3.10) |
Wir können also die Distanz
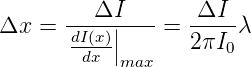 | (3.11) |
noch bestimmen. Dazu muss die Position (die Phase) so gelegt werden, dass der Sinus extremal ist:
Wir bekommen so den Arbeitspunkt 8πxopt = (2j + 1)πλ oder
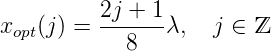 | (3.13) |
Maxima der Intensität am Ausgang liegen aber bei
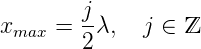 | (3.14) |
und die Minima bei
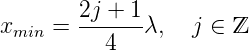 | (3.15) |
Wenn zum Beispiel λ = 500 nm ist und ΔI∕I0 = 0.01 ist, liegt der erste optimale Arbeitspunkt bei x = 67.5 nm und die mögliche Auflösung beträgt Δx = 0.8 nm.
Das Michelson-Interferometer wird häufig zur Messung von Distanzen verwendet.
Bei besserem Signal-Rauschverhältnis, können kleinere Längenänderungen bestimmt werden. Wenn ein Signal-Rausch-Verhältnis von etwa 10−13 erreicht wird, können Gravitationswellen detektiert werden.
| Literatur | |
__________________________________________________________________________
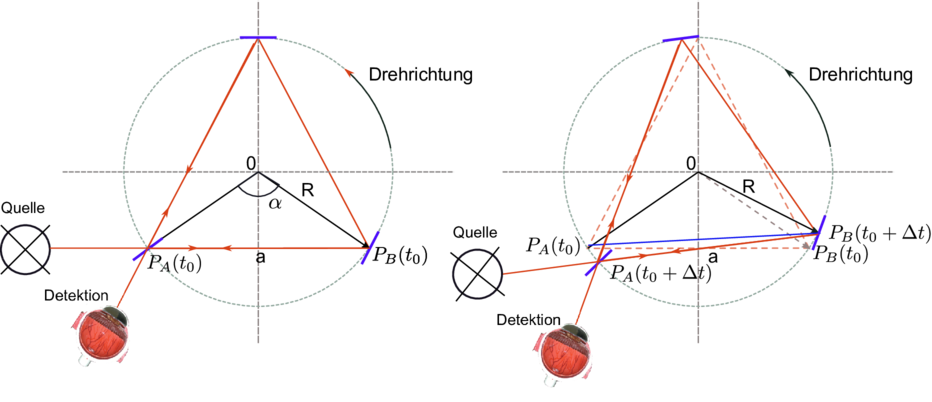
Sagnac-Interferometer. Rechts nach einer Laufzeit.
_____________________________________________________________________
Beim Sagnac Interferometer läuft das Licht links- und rechts herum und interferiert dann. Die Lichtwege sind identisch, das Verschieben eines Spiegels erzeugt kein Signal. Wenn man das Sagnac-Interferometer jedoch mit der Kreisfrequenz Ω dreht, dann sind die Umlaufzeiten mit und gegen die Drehrichtung unterschiedlich. Die Behauptung ist, dass der Laufzeitunterschied zwischen der links- und der rechtsläufigen Welle
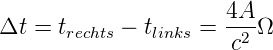 | (3.16) |
ist. Dabei ist Ω die Winkelfrequenz, mit der das Interferometer rotiert, A die vom Licht eingeschlossene Fläche (in Abbildung 3.2.4 die Fläche des Dreieckes) und c die Vakuumlichtgeschwindigkeit. Sagnac-Interferometer werden heute als Gyroskope verwendet. Sie messen zum Beispiel die Drehraten von Flugzeugen und werden so zur magnetfeldunabhängigen Navigation herangezogen.
Wir betrachten ein Interferometer aus n Seiten. Die Fläche
des n-Ecks is n-,mal die Fläche eines einzelnen Dreiecks,
und dessen Fläche AD = ah∕2. Beim n-Eck ist die Höhe
h = R cos 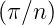 und die Grundlinie a = 2R sin
und die Grundlinie a = 2R sin 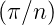 . Damit
ist
. Damit
ist
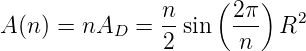 | (3.17) |
Wir brauchen nun die Strecke PA(t0)PB(t0 + Δt). Diese ist die Grundlinie in einem gleichschenkligen Dreieck mit dem Spitzenwinkel
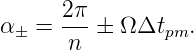 | (3.18) |
Mit ± können beide Fälle gleichzeitig behandelt werden. Wir brauchen noch den Winkel an der Grundlinie (zweimal der gleiche Winkel β±
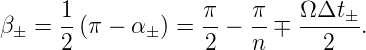 | (3.19) |
Mit dem Sinussatz für beliebige Dreiecke bekommen wir die Länge der Grundlinie
Die Zeit Δt± ist sowohl die Laufzeit von PA(t0) nach PB(t0 + Δt±) wie auch die Zeit, in der sich das Interferometer dreht. Wir haben also die Gleichungen
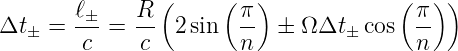 | (3.22) |
welche gelten wenn  «
« 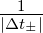 gilt. Die Lösungen
sind
gilt. Die Lösungen
sind
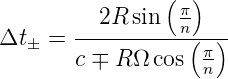 | (3.23) |
Damit ist der Laufzeitunterschied (und daraus kann die Phase berechnet werden)
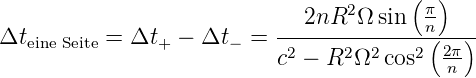 | (3.24) |
Auch dieser Ausdruck kann entwickelt werden wenn
 «
«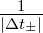 ist. Wir erhalten die linearisierte Gleichung,
ist. Wir erhalten die linearisierte Gleichung,
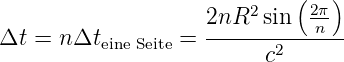 | (3.25) |
und, wennn wir die Fläche A(n) des n-Ecks einsetzen
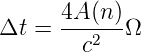 | (3.26) |
Diese Gleichung müsste eigentlich mit der allgemeinen Relativitätstheorie hergeleitet werden. Für langsame Drehungen ist das Resultat jedoch korrekt. Bei einem kreisförmigen Sagnac-Interferometer (z.B. mit whispering gallery modes) ist
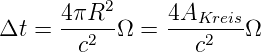
genau so gross. Mit c = Δs∕Δt folgt
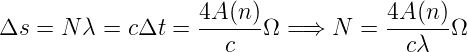 | (3.27) |
Beispiel: Mit Ω = 2π s−1, A(n) = 0.01 m2 und λ = 632 nm (HeNe-Laser) erhält man N = 0.00132648 Dies ist eine kleine Zahl, kann aber mit Modulationstechniken problemlos gemessen werden.
| Literatur | |
Aus den Fresnelschen Gleichungen sind die Transmissionskoeffizienten für Amplituden für die beiden Polarisationsrichtungen p und s bekannt. Wir setzen nach den Gleichungen (2.27) und (2.33) können wir winkel- und polarisationsabhängige Transmissions- und Reflexionskoeffizienten definieren.
Für die Reflexion haben wir
![(
{ − ssinin((αα−+γγ((αα)))), s-Polarisation (2.27);
r = ( tan[α−-γ(α)]
tan[α+ γ(α)], p-Polarisation (2.33) .](op-2016-2017235x.png) | (3.28) |
Analog schreiben wir für die Transmission
![(
{ 2sinγ(α)cosα-, s-Polarisation (2.27);
t = sin(α2+siγn(αγ)(α))cosα
( sin[α+-γ(α)]cos[α−-γ(α)], p-Polarisation (2.33) .](op-2016-2017236x.png) | (3.29) |
Im Weiteren sind mit t und r immer diese Koeffizienten aus den Fresnelschen Formeln gemeint.
| Versuch zur Vorlesung: | |
| Interferenz an dünnen Schichten als Beispiel für das Fabry-Perot-Interferometer (Versuchskarte O-085) | |
_______________________________________________
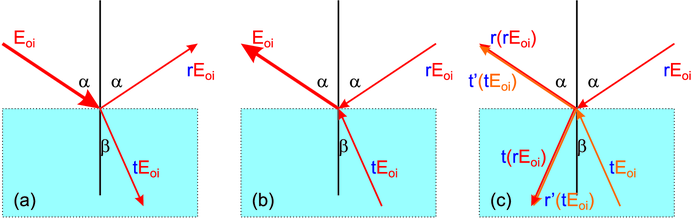
Stokessche Behandlung von Reflexion und Brechung (nach Hecht [Hec05])
_____________________________________________________________________
Wir nehmen an, dass eine Welle mit der Amplitude 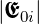 ,
die vom oberen Medium her auf die Grenzfläche auftritt, mit
dem Faktor r reflektiert wird, sowie mit dem Faktor t
gebrochen wird. Die Amplitude der gebrochenen Welle ist
dann t
,
die vom oberen Medium her auf die Grenzfläche auftritt, mit
dem Faktor r reflektiert wird, sowie mit dem Faktor t
gebrochen wird. Die Amplitude der gebrochenen Welle ist
dann t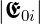 , die der reflektierten Welle r
, die der reflektierten Welle r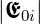 . Das Fermatsche
Prinzip bedeutet, dass auch die zeitumgekehrte Situation eine
physikalisch realisierbare ist. Also ist auch die Strahlführung
im Teilbild (b) oben eine realisierbare Situation. Dabei
müssen wir uns klar machen, dass sowohl die einfallende Welle
mit der Amplitude r
. Das Fermatsche
Prinzip bedeutet, dass auch die zeitumgekehrte Situation eine
physikalisch realisierbare ist. Also ist auch die Strahlführung
im Teilbild (b) oben eine realisierbare Situation. Dabei
müssen wir uns klar machen, dass sowohl die einfallende Welle
mit der Amplitude r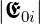 und diejenige mit t
und diejenige mit t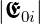 eine
reflektierte und eine transmittierte, gebrochene Welle
erzeugen. Dabei ist für die Welle, die von unten kommt der
Reflexionsfaktor r′ und der Transmissionsfaktor t′. Die
Situation in (c) ist nur dann äquivalent zu der in (b), wenn
gilt
eine
reflektierte und eine transmittierte, gebrochene Welle
erzeugen. Dabei ist für die Welle, die von unten kommt der
Reflexionsfaktor r′ und der Transmissionsfaktor t′. Die
Situation in (c) ist nur dann äquivalent zu der in (b), wenn
gilt
Damit erhält man eine Verknüpfung der Reflexions- und Brechungskoeffizienten für den Übergang vom Medium 1 in das Medium 2 und umgekehrt. Dabei sind α und β die jeweiligen Einfallswinkel, die durch das Snelliussche Gesetz verknüpft sind.
Diese beiden Gleichungen heissen die Stokeschen Relationen. Die zweite Gleichung zeigt, dass wenn r für die Reflexion am dichteren Medium steht, bei der es nach den Fresnelschen Formeln einen Phasensprung von π gibt, dass dann bei der Reflexion am optisch dünneren Medium kein Phasensprung auftritt.
__________________________________________________________________________
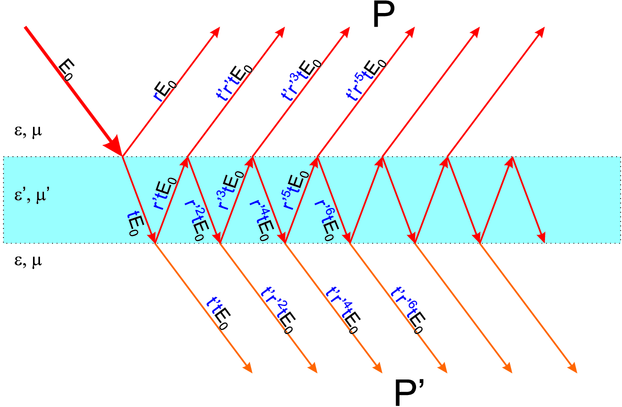
Strahlengang bei einem Fabry-Perot-Etalon (nach Hecht
[Hec05]). Dabei ist in der Zeichnung 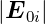 =
= 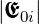 gesetzt worden.
gesetzt worden.
_____________________________________________________________________
Wir betrachten nun die Reflexion an einem Etalon, also einer Glasplatte mit dem Brechungsindex nG mit planparallelen Oberflächen. Im Aussenraum sei auf beiden Seiten n = 1. Die Abbildung zeigt die reflektierten und gebrochenen Strahlen, wobei die Konvention der Gleichung (3.31) verwendet wurde. Die reflektierten Strahlen interferieren in dem weit entfernten Punkt P, die transmittierten Strahlen im weit entfernten Punkt P′.
__________________________________________________________________________
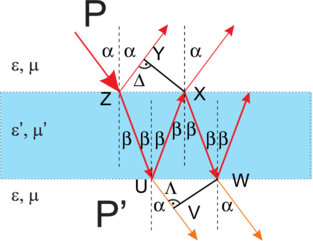
Strahlengang bei einem Fabry-Perot-Etalon (nach Pérez [Pér96, p. 392])
_____________________________________________________________________
Für das transmittierte Licht ist der Weglängenunterschied durch den Unterschied der optischen Wege UV und UXW, Λ = UXW −UV der relevante Unterschied. Die Strecke UXW ist im Medium mit dem Brechungsindex nG, im Glas. Der optische Weg ist dann
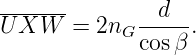 |
Weiter ist die Strecke UV durch UW sin α gegeben. Weiter ist aber auch UW = 2d tan β, eine rein geometrische Überlegung, die keine optischen Wege beinhaltet. Zusammen bekommen wir
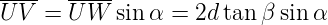 |
Damit ist Λ für ein Etalon der Dicke d
Der Gangunterschied für die Reflexion Δ kann aus dem Gangunterschied für die Transmission abgeleitet werden, wobei ein Phasensprung von π berücksichtigt werden muss. Wir haben mit ZUX = UXW und ZY = UV
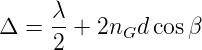 | (3.33) |
Bei den Strahlen, die in P interferieren, ist die Anzahl der inneren Reflexionen ungerade. Für den Spezialfall des senkrechten Einfalls, oder bei senkrechter Polarisation, ergeben die Reflexionen keine Phasenänderung. Wenn Λ = mλ ist, haben in P alle Wellen die gleiche Phase, ausser der ersten, deren Phase wegen r′ = −r um π ändert. Also ist die reflektierte Amplitude
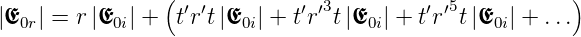 | (3.34) |
Da Λ = mλ und damit die innere Phasenverschiebung 0 ist, ersetzen wir r′ mit −r und erhalten
![[ ′ ( 2 4 )]
|E0r| = |E0i| r − trt 1 + r + r + ...](op-2016-2017251x.png) | (3.35) |
Diese geometrische Reihe konvergiert bei r2 < 1 gegen 1∕(1 −r2), so dass wir
![[ ] ( )
t′rt tt′
|E0r| = |E0i| r − -----2 = |E0i|r 1 − -----2
1 − r 1 − r](op-2016-2017252x.png) | (3.36) |
Nach den Stokeschen Relationen ist tt′ = 1 −r2 und damit die reflektierte Amplitude bei senkrechtem Einfall
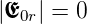 | (3.37) |
Also wird im Falle Λ = mλ = 2nGd cos β oder d cos β = 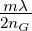 alles Licht transmittiert.
alles Licht transmittiert.
Der zweite Spezialfall ist Λ = 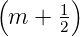 λ). Dann sind
die relativen Phasen benachbarter Wellen, unter der
Berücksichtigung dass r′ = −r und dass die innere Phase π
ist, die Phasenverschiebung π, ausser bei den ersten beiden
Wellen, die gleichphasig sind. Wir erhalten für die skalare
Amplitude
λ). Dann sind
die relativen Phasen benachbarter Wellen, unter der
Berücksichtigung dass r′ = −r und dass die innere Phase π
ist, die Phasenverschiebung π, ausser bei den ersten beiden
Wellen, die gleichphasig sind. Wir erhalten für die skalare
Amplitude
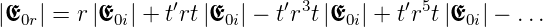 | (3.38) |
oder
![[ ( )]
|E | = |E |r 1 + t′t 1 − r2 + r2 − ...
0r 0i](op-2016-2017257x.png) | (3.39) |
Die Reihe in der Klammer konvergiert gegen 1∕(1 + r2). Wir erhalten also
![[ ]
t′t
|E0r| = |E0i|r 1 + -----2
1 + r](op-2016-2017258x.png) | (3.40) |
Mit t′t = 1 −r2 erhalten wir
![[ 2] 2 2
|E0r| = |E0i|r 1 + 1 −-r- = |E0i|r 1 +-r-+-1-−-r--= |E0i|--2r--
1 + r2 1 + r2 1 + r2](op-2016-2017259x.png) | (3.41) |
Damit wird die reflektierte Intensität maximal, nämlich
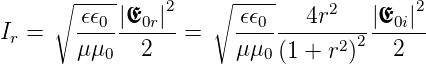 | (3.42) |
Den allgemeinen Fall kann man berechnen, indem man die
durch die einfallende Welle 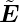 0(t) =
0(t) = 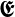 0ieiωt angeregten
reflektierten Teilwellen aufschreibt, wobei zwischen zwei
Teilwellen die Phasenverschiebung δ = k0Λ ist. Wir betrachten
eine definierte Polarisationsrichtung s oder p, so dass wir
betragsmässig schreiben können
0ieiωt angeregten
reflektierten Teilwellen aufschreibt, wobei zwischen zwei
Teilwellen die Phasenverschiebung δ = k0Λ ist. Wir betrachten
eine definierte Polarisationsrichtung s oder p, so dass wir
betragsmässig schreiben können
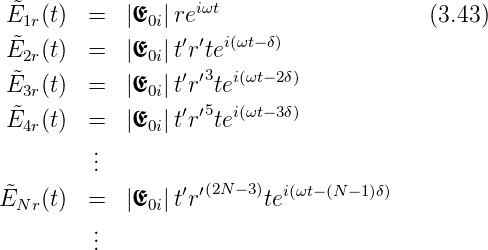
Die resultierende Welle ist die Summe aller Teilwellen
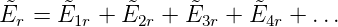 | (3.44) |
Eingesetzt erhalten wir die Summe
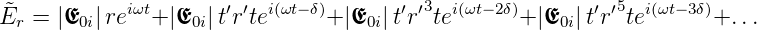 | (3.45) |
Zusammengefasst kann diese so umgeschrieben werden
![{ [ ]}
˜Er = |E0i|eiωt r + t′r′te−iδ 1 + r′2e−iδ + r′4e−i(2δ) + r′6e−i(3δ) + ... (3.46)
{ [ ( ) ( ) ( ) ]}
= |E |eiωt r + t′r′te− iδ 1 + r′2e−iδ 1 + r′2e−iδ 2 + r′2e− iδ 3 + ...
0i](op-2016-2017266x.png)
Für 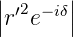 < 1 konvergiert die geometrische Reihe. Wir
erhalten
< 1 konvergiert die geometrische Reihe. Wir
erhalten
![[ ]
iωt t′r′te−iδ
˜Er = |E0i|e r + 1 −-r′2e−iδ-](op-2016-2017268x.png) | (3.47) |
Mit den Stokeschen Relationen r′ = −r und t′t = 1 −r2 bekommen wir
![[ ] [ ]
iωt r(1 − r2)e−iδ iωt r(1 − e− iδ)
˜Er = |E0i|e r − -1-−-r2e−-iδ-- = |E0i|e -1 −-r2e−iδ](op-2016-2017269x.png) | (3.48) |
Die reflektierte optische Intensität ist Ir = 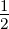
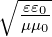 ẼrẼr∗ und
somit
ẼrẼr∗ und
somit
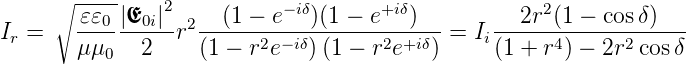 | (3.49) |
Mit einer analogen Ableitung berechnet man die transmittierte Intensität
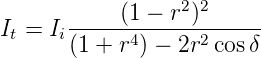 | (3.50) |
da das transmittierte Licht sich im gleichen Medium wie das einfallende Licht sich bewegt. Mit cos δ = 1 − 2 sin 2(δ∕2) werden It und Ir
Wir haben dabei angenommen, dass keine Energie absorbiert wird 1 . Dann ist Ii = It + Ir. Ein Maximum in der Transmission erhält man, wenn der Nenner möglichst klein, das heisst, dass in Gleichung (3.50) cos δ = 1 ist. Dann ist
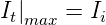 | (3.52) |
und
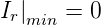 | (3.53) |
Umgekehrt ist die Transmission minimal, wenn der Nenner bei It maximal ist, also wenn in Gleichung (3.50) cos δ = −1 ist
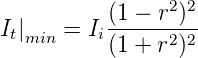 | (3.54) |
und
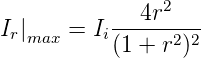 | (3.55) |
Es hat sich eingebürgert, dass Fabry-Perot-Interferometer mit der Kennzahl Finessefaktor charakterisiert werden:
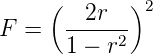 | (3.56) |
Dann gilt für die Intensitätsverhältnisse
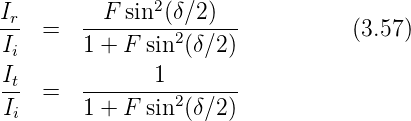
wobei die Funktion ![[1 + F sin2(δ∕2 )]](op-2016-2017281x.png) −1 = A(δ) auch Airy-Funktion
genannt wird2 .
−1 = A(δ) auch Airy-Funktion
genannt wird2 .
__________________________________________________________________________
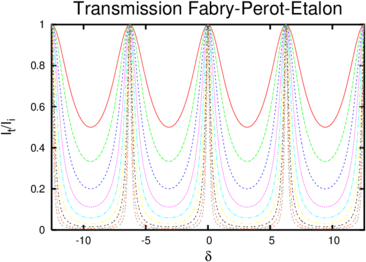
Transmission durch ein Fabry-Perot-Etalon in Abhängigkeit von der Finesse F. Von oben nach unten sind die Transmissionskurven für F = 1, F = 2, F = 4, F = 8, F = 16, F = 32, F = 64, F = 128 und F = 256 dargestellt.
_____________________________________________________________________
_____________________________________________________________________
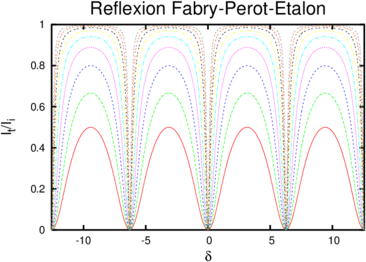
Reflexion an einem Fabry-Perot-Etalon in Abhängigkeit von der Finesse F. Von unten nach oben sind die Reflexionskurven für F = 1, F = 2, F = 4, F = 8, F = 16, F = 32, F = 64, F = 128 und F = 256 dargestellt.
_____________________________________________________________________
Die Halbwertsbreite der Transmissionskurven ist durch
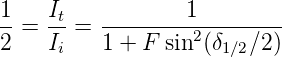 | (3.58) |
gegeben. Daraus folgt
 | (3.59) |
Das Verhältnis des Abstandes benachbarter Maxima zu der Halbwertsbreite heisst Finesse und ist
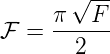 | (3.60) |
Die einfachsten Fabry-Perot-Spektrometer haben ein F ≈ 30. Werte von F ≈ 1000 sind an der Grenze des technisch machbaren. Wenn bei dem Fabry-Perot-Spektrometer Absorption vorhanden ist, müssen kompliziertere Gleichungen, die Sie zum Beispiel in Hecht [Hec05, 617] finden, verwendet werden.
Die Wellenfronten in Interferometern sind nicht eben sondern in erster Näherung sphärisch. Jedes Interferometer hat eine endliche Ausdehnung. Licht wird deshalb an den Bauteilen des Interferometers gebeugt. Seine Flächen gleicher Phase sind also gekrümmt. Dies wird im Kapitel 7.3 über Gausssche Strahlen noch weiter ausgeführt.
__________________________________________________________________________
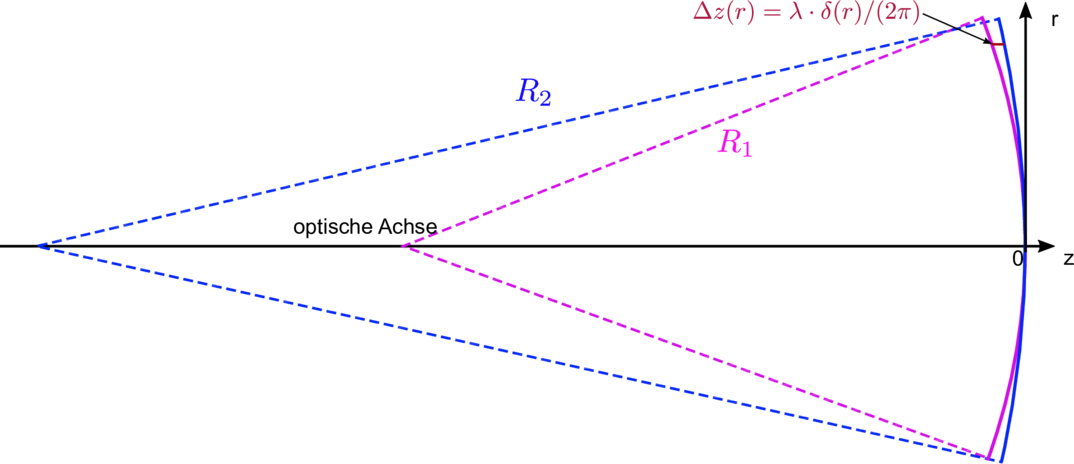
Geometrie zur Berechnung der Ringmuster in Interferometern
_____________________________________________________________________
Wir haben nach Abbildung 3.2.6 mit r2 = x2 + y2 in der xy-Ebene
Gleichung (3.61c) zeigt, dass die Phase der durch die Interferenz resultierenden Welle proportional zu r2 ist.
__________________________________________________________________________
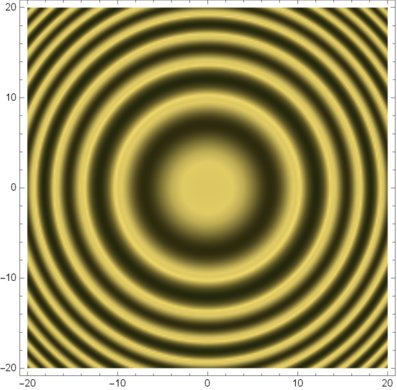
Simulation der Interferenzringe nach (3.61c) mit R1∕λ = 50, R2∕λ = 100
__________________________________________________________________________
Abbildung 3.2.6 zeigt eine Simulation dieser Ringe.
__________________________________________________________________________
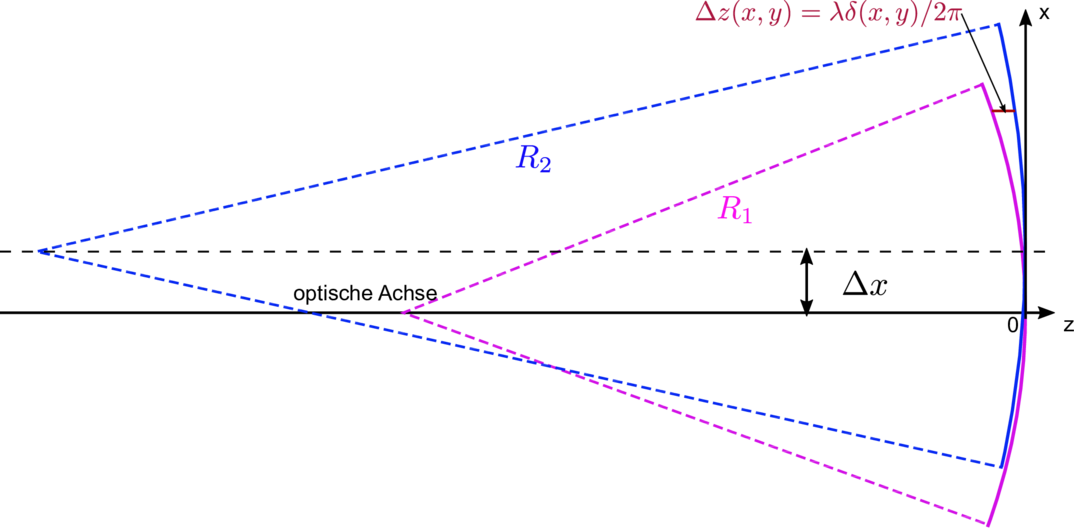
Geometrie zur Berechnung der Streifenmuster in Interferometern
_____________________________________________________________________
Oftmals sind die Strahlen seitlich versetzt. Abbildung 3.2.6 zeigt die neue Geometrie. Dies führt zu
Gleichung (3.62c) zeigt, dass das Muster aus Ringen aus Gleichung (3.61c) mit einer linearen Phase überlagert wird.
__________________________________________________________________________
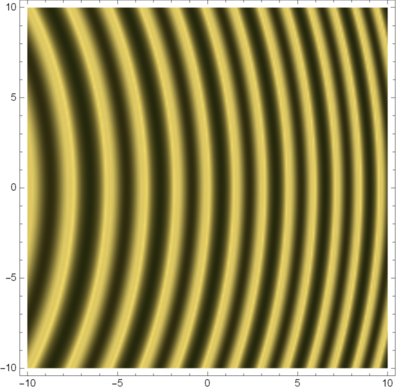
Simulation der Interferenzringe nach (3.62c) mit R1∕λ = 50, R2∕λ = 100 und Δx∕λ = 10.
_____________________________________________________________________
Dies führt, wie in Abbildung 3.2.6 gezeigt zu streifenförmigen gekrümmten Interferenzmustern.
 Lizenzinformationen
Lizenzinformationen