
| Abbildung 2.1.: | Ein grundlegender Systemblock |

Elektronische Schaltungen wie auch ganze elektronische Messgeräte können als Systeme betrachtet werden. Die einzelnen Baublöcke sind entweder grundlegende Systeme, oder sie können als Zusammenfassung von verschiedenen einfacheren Systemen betrachtet werden. Je nach Tiefe der Betrachtung ist zum Beispiel ein Lock-In Verstärker ein grundlegendes System mit einer, durchaus nicht trivialen Beziehung zwischen Ausgangs- und Eingangssignalen. Alternativ kann er aber auch als Zusammensetzung der folgenden Baugruppen aufgefasst werden:
Diese Liste könnte, wenn man wollte, noch weiter unterteilt werden.
Es ist üblich geworden, die folgenden Symbole für die Darstellung von Systemen zu verwenden[DISW76].
Die Abbildung 2.1 zeigt ein einen solchen grundlegenden Systemblock. Das Wort Block in dieser Darstellung wird, je nach Typ oder Übertragungsfunktion ausgewechselt. Die Anschlüsse werden mit Pfeilen versehen, um den Signalfluss darzustellen. So würde man zum Beispiel eine Differentiation wie in Abbildung 2.2 darstellen.
Eine Integration könnte wie in Abbildung 2.3 aussehen.
In allen Darstellungen ist es optional, die Bezeichnungen Eingang und Ausgang zu verwenden. Sie sollten benutzt werden, wenn der Signalfluss aus der Darstellung nicht eindeutig abgelesen werden kann. Die einzelnen Blöcke werden mit Linien verbunden. Sollten ein Ausgang eines Blocks auf mehrere Eingänge aufgeteilt werden, so werden Abnahmepunkte wie in Abbildung 2.4 verwendet.
Abnahmepunke dienen nicht nur dazu, Signale nach vorne zu leiten. Wie Abbildung 2.5 zeigt, können auch Rückkoppelungen mit dieser Formensprache gehandhabt werden.
Um allgemeine Signalflüsse darstellen zu können, sind noch Summationspunkte notwendig. Sie werden wie in Abbildung 2.6 dargestellt. Es können zwei oder mehr Summationseingänge verwendet werden.
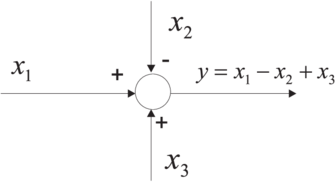
| Abbildung 2.6.: | Ein Summationspunkt. Die Operatoren + und - geben an, ob addiert oder subtrahiert werden soll |
Wir können nun diese Formensprache verwenden, um die Differentialgleichung
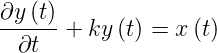 | (2.1) |
darzustellen. Wir schreiben die Gleichung (2.1) um, so dass wir sie in die Blockschaltbildform bringen können. Zuerst isolieren wir die Ableitung.
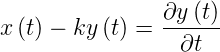 | (2.2) |
Schliesslich integrieren wir die Gleichung (2.2) und erhalten
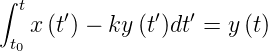 | (2.3) |
Die Gleichung (2.1) in der Form (2.3) kann nun wie in Abbildung 2.7 dargestellt werden.
Die Umstellung in der Gleichung musste durchgeführt werden, um y(t) zu isolieren. Eine alternative Art der Umformung ist
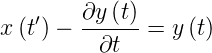 | (2.4) |
Das entsprechende Blockschaltbild ist in der Abbildung 2.8 zu sehen.
Wenn man die Abbildungen 2.7 und 2.8 vergleicht,
sieht man, dass die gleiche Differentialgleichung auf zwei
verschiedene Arten dargestellt werden kann. Es gibt
offensichtlich Regeln, die einem ermöglichen, die Umstellung
auf rein formalem Wege zustande zu bringen. Der Vergleich
der beiden Abbildungen sagt zum Beispiel, dass wenn k in
einem nach links gerichteten Zweig vorkommt, wir 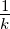 in einen
nach rechts gerichteten Zweig einsetzen müssen. Ebenso sind
die Integration und die Differentiation ein Paar, wenn wir in
einem Signalzweig die Signalflussrichtung wechseln. Im
nächsten Abschnitt 2.1.2 werden die Rechenregeln für
Blockschemata dargestellt.
in einen
nach rechts gerichteten Zweig einsetzen müssen. Ebenso sind
die Integration und die Differentiation ein Paar, wenn wir in
einem Signalzweig die Signalflussrichtung wechseln. Im
nächsten Abschnitt 2.1.2 werden die Rechenregeln für
Blockschemata dargestellt.
Zum Schluss dieses Abschnittes sei darauf hingewiesen, dass für Operationsverstärker die genau gleichen Regeln gelten: Ein Bauelement, das differenziert eingebaut in die Rückkoppelschleife, bewirkt, dass die Gesamtschaltung integriert. Mit diesem Konzept, das im Kapitel 3 besprochen wird, können unter anderem grosse Impedanzen oder Zirkulatoren realisiert werden.
Das Rechnen mit Blockschemata erlaubt, auf eine standardisierte Weise die Umorganisation und die Berechnung von Schaltungen. Diese Rechnungen werden benötigt, um Schaltungen zu vereinfachen oder um sie, bei gleicher Funktion, anders zu strukturieren. Dies kann nötig sein, weil Toleranzen und Fehler der Bauteile nicht bei jeder Konfiguration sich gleich auswirken.
Wenn zwei Blöcke mit den Transferfunktionen G1 und G2 hintereinander geschaltet sind, dann können diese durch einen Block mit der Transferfunktion G1G2 ersetzt werden (Abbildung 2.9).
Für lineare Systeme ist die Reihenfolge, in der zwei Blöcke mit kommutativen Operatoren (Multiplikation, aber auch die Ableitung einer komplexen Funktion) angeordnet werden, unerheblich. Dies wird mit dem Kommutativgesetz G1G2 = G2G1 beschrieben (Abbildung 2.10). Während diese Aussage mathematisch gesehen korrekt ist, kommt es bei der Realisierung durchaus auf die Reihenfolge an. Da reale Baublöcke immer nichtlinear sind (Begrenzung, Rauschen, Wechselwirkung) kann die Platzierung darüber entscheiden, ob ein Design gut oder schlecht ist.
|
| Transformation | Gleichung | Ausgangsdiagramm | Äquivalentes Diagramm |
| 1 | Reihenschaltung | y = (G2G1)x |
|
|
| 2 | Parallelschaltung | y = G1x ±G2x |
|
|
| 3 | In Vorwärtsrichtung parallelgeschalteten Block entfernen | y = G1x ±G2x |
|
|
| 4 | Block in der Rückkopplungsleitung entfernen | y =
G1 |
|
|
| 5 | Block aus Rückkoppelleitung verschieben | y =
G1 |
|
|
| Tabelle 2.1.: | Algebra mit Blockdiagrammen: Kombination von Blöcken |
|
| Transformation | Gleichung | Ausgangsdiagramm | Äquivalentes Diagramm |
| 6a | Summationspunkteverschieben | z = w ±x ±y |
|
|
| 6b | Summationspunkteverschieben | z = w ±x ±y |
|
|
| 7 | Summationspunkt vor Block schieben | z = Gx ±y |
|
|
| 8 | Summationspunkt nach Block schieben | z = G |
|
|
| Tabelle 2.2.: | Algebra mit Blockdiagrammen: Summationspunkte verschieben |
|
| Transformation | Gleichung | Ausgangsdiagramm | Äquivalentes Diagramm |
| 9 | Abnahmepunkt vor Block schieben | y = Gx |
|
|
| 10 | Abnahmepunkt nach Block schieben | y = Gx |
|
|
| 11 | Abnahmepunkt vor einen Summationspunkt schieben | z = x ±y |
|
|
| 12 | Abnahmepunkt nach einen Summationspunkt schieben | y = x ±y |
|
|
| Tabelle 2.3.: | Algebra mit Blockdiagrammen:Abnahmepunkte verschieben |
Ein rückgekoppeltes System, eine der am häufigsten vorkommenden Strukturen in der Physikalischen Elektronik und Messtechnik, sieht wie in Abbildung 2.11 aus. Wenn man die Konventionen aus der Abbildung 2.11 verwendet und insbesondere beachtet, dass das obere Vorzeichen des Zweiges B eine Gegenkopplung bedeutet, so erhält man die folgenden universellen Beziehungen:
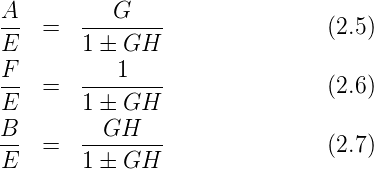
Hier ist E das Eingangssignal, A das Ausgangssignal und B
das Rückkoppelsignal vor dem Summationspunkt und F das
Fehlersignal. Eine Analyse der obigen Gleichungen zeigt, dass
wenn der Betrag von H gross ist bei einer negativen
Rückkoppelung, also bei einem positiven Vorzeichen, dass 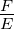 beliebig klein wird. B wird dann gleich dem negativen
Eingangssignal E.
beliebig klein wird. B wird dann gleich dem negativen
Eingangssignal E.
 Lizenzinformationen
Lizenzinformationen