©2002-2017 Ulm University, Othmar Marti, 
[Nächste
Seite] [Vorherige Seite] [vorheriges Seitenende] [Seitenende]
[Ebene nach oben] [PDF-Datei][Epub-Datei][Andere
Skripte]
3.1 Halbleiter–Grundlagen
3.1.1 Grundlagen
Die heutige Elektronik ist im Wesentlichen eine
Festkörperelektronik. Von zentraler Bedeutung sind dabei
einkristalline Halbleiter. So sind über 95 % aller kommerzieller
Chips aus einkristallinem Si. Polykristalline und amorphe
Halbleiter werden selten eingesetzt. Oxide, Polymere und
Metalle sind von sekundärer Bedeutung; allerdings wirft
beispielsweise die Herstellung eines isolierenden Gateoxids,
von Photolacken oder verlustarmer ohmscher Kontakte und
elektrischer Zuleitungen hochinteressante physikalische,
chemische und technologische Fragen auf.
Der Begriff Halbleiter bezieht sich auf die elektrische
Leitfähigkeit bzw. den spezifischen Widerstand reiner
Materialien. Bei 300K zeigen Isolatoren spezifische Widerstände
von > 108Ωcm, ein guter Isolator > 1015Ωcm; Metalle
dagegen < 10−4Ωcm, Halbmetalle von 102 − 104Ωcm.
Reine Halbleiter können durch gezielte Verunreinigungen
(Dotierung) die Lücke zwischen Isolator und Metall ausfüllen,
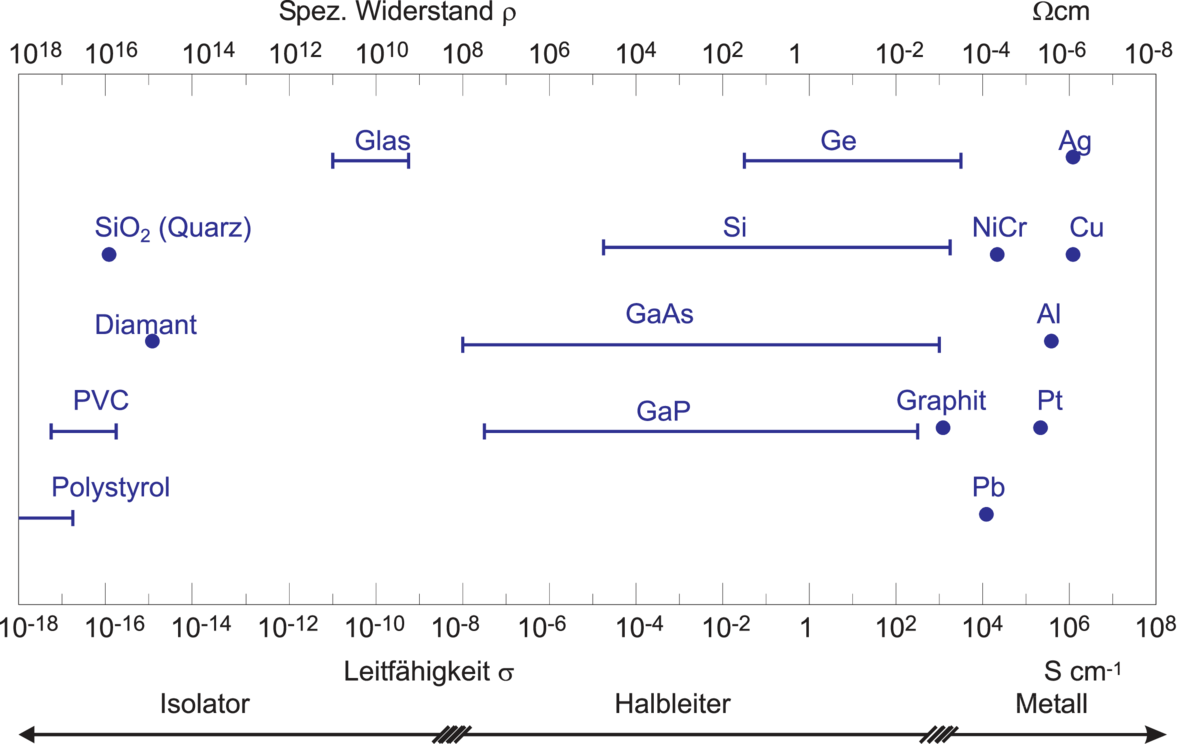
vgl. Bild 3.1.1. Das Temperaturverhalten der Leitfähigkeit
von Metallen und Halbleitern unterscheidet sich aber
wesentlich.
__________________________________________________________________________
Leitfähigkeit und spezifischer Widerstand von Metallen,
Halbleitern und Isolatoren bei Zimmertemperatur.
(gezeichnet nach Paul [Pau89])
_____________________________________________________________________
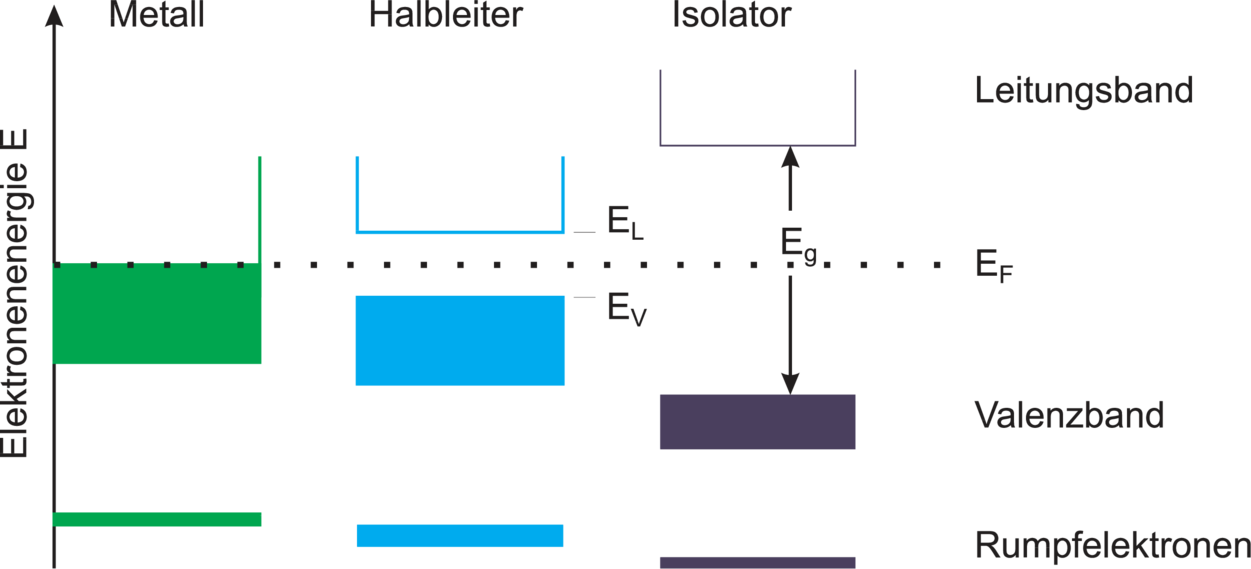
Ein Blick auf das Energie–Termschema bzw. genauer das
Energie–Bandschema in Abbildung 3.1.1 soll nochmals an die
physikalischen Grundlagen erinnern.
__________________________________________________________________________
Energieschema für Metall, Halbleiter und Isolator;
schraffiert: besetzte Zustände. EF: Fermi–Niveau, EG:
Bandlücke, EL: Leitungsbandunterkante (Unterkante des
niedrigsten leeren Bandes), EV: Valenzbandoberkante
(Oberkante des höchsten gefüllten Bandes), Skizze nach
[IL99]
_____________________________________________________________________
Metalle haben bei T = 0K ein teilweise besetztes Band; bei
Halbleitern und Isolatoren ist das vollständig besetzte
Valenzband vom vollständig entleerten Leitungsband durch
eine Bandlücke getrennt. Bei ideal reinen Materialien liegt die
Fermi-Energie in der Bandlückenmitte. Da nur partiell
gefüllte elektronische Bänder elektrischen Strom tragen
können, sind bei T = 0K auch Halbleiter isolierend. Bei
erhöhten Temperaturen, z. B. Raumtemperatur, und nicht zu
grossen Energielücken, z. B. 1, 5eV, werden genügend
Elektronen aus dem Valenzband ins Leitungsband angehoben,
um eine merkliche elektrische Leitfähigkeit zu erhalten.
(Wir werden noch sehen, dass ausser den Elektronen
im Leitungsband auch die ’Löcher’ im Valenzband zur
Leitfähigkeit des Halbleiters beitragen.) Dagegen ist die
Bandlücke bei Isolatoren so gross, dass auch bei einigen
100°C keine technisch relevante Leitfähigkeit beobachtet
wird.
Halbleitende Materialien können aus Elementen,
Verbindungen und Legierungen bestehen. Die Elementhalbleiter
stehen in der IV. Hauptgruppe des Periodensystems: C
(Diamant, 5, 47eV), Si (engl. silicon, 1, 10eV), Ge (0, 67eV)
und α–Sn (0, 08eV); mit zunehmender Ordnungszahl nimmt
— typischerweise — die Energie der Energielücke (bei 300K)
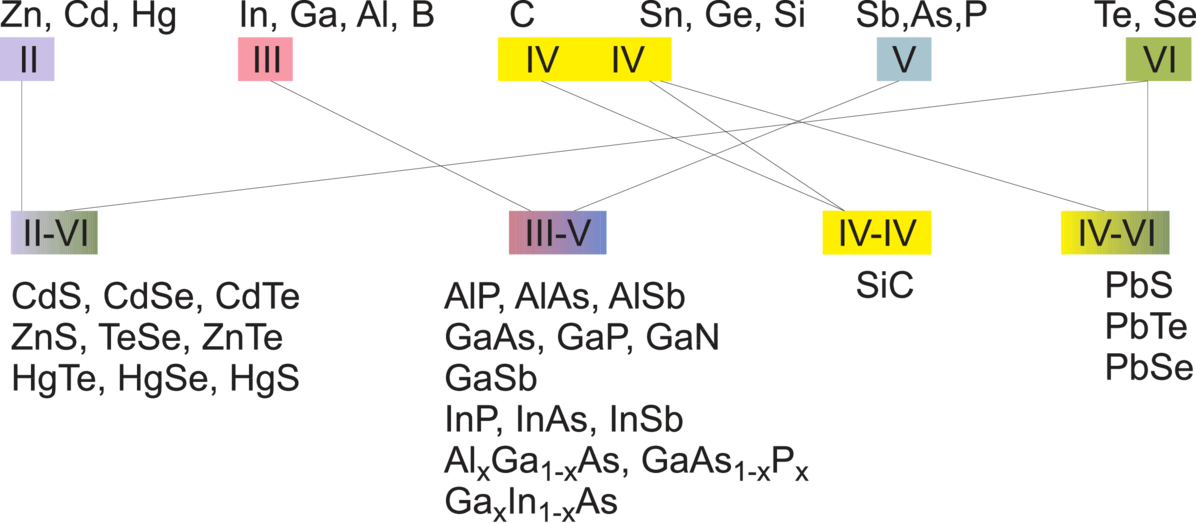
ab. Binäre Verbindungshalbleiter realisiert die Natur auf
verschiedene Weisen: Aus IV–IV–Elementen wie SiC
(3, 26eV), aus III-V-Elementen wie GaAs und GaN, aus
II–VI–Elementen wie CdS und, nicht unmittelbar einzusehen,
aus IV–VI–Elementen wie PbS.
Von zunehmend technologischer Bedeutung sind
schliesslich GexSi1−x–Schichten auf Si–Substraten.
Ternäre Verbindungshalbleiter wie AlxGa1−xAs oder
GaxIn1−xAs sind die wesentlichen Baustoffe der modernen
Kommunikationstechnologie; der erste blaugrüne cw–HL–Laser
bestand aus einem Schichtsystem aus ZnCdSe / ZnSSe /
ZnMgSSe (Schicht 3: quaternärer Halbleiter).
Die beeindruckende Vielfalt schlägt sich auch in der
Vielzahl der realisierten Kristallstrukturen fort. So finden
wir beispielsweise das Diamantgitter bei C, Ge, Si, das
Zinkblendegitter bei ZnS, GaAs, GaP, etc., das Wurzitgitter
bei CdS, ZnS (beides möglich), etc., das Kochsalzgitter bei
PbS, PbTe, etc. und schliesslich weisen Dichalcogenide wie
WSe2, WS2, MoS2, MoTe2 (nicht aber WTe2) eine dem
Graphit ähnliche Schichtstruktur auf.
Eine Vorhersage aus ‘first principles’, ob ein Stoff bei
Raumtemperatur halbleitend sein wird oder nicht fällt schwer;
am besten gelingt dies noch bei Ge und Si. Ansonsten
hilft nur die enge Kombination von Experiment und
Bandstrukturrechnung.
Bei den Elementhalbleitern C, Si und Ge liegt die kovalente
Bindung in ihrer reinsten Form vor. Zur Erinnerung: Bei der
quantenmechanischen Behandlung des H2+–Molelüls lernten
Sie das Überlappen der Einzelatomzustände erstmals kennen.
Näherungsweise wird dort die neue Wellenfunktion durch eine
Linearkombination der Einzelwellenfunktionen beschrieben.
Ψ+ = Ψa + Ψb bildet den bindenden, energetisch (im Vergleich
zum Ausgangszustand) tiefer liegenden Grundzustand aus;
d. h. die Elektronendichte zwischen den Atomkernen wird
erhöht und so ihre Coulomb–Abstossung reduziert. Der
bindende Grundzustand ist (Spinentartung, Pauli–Prinzip)
mit zwei Elektronen besetzbar. Der antibindende Zustand
Ψ− = Ψa − Ψb liegt energetisch höher als die Ausgangszustände.
Beim analog zu behandelnden H2–Molekül bezeichnen wir
diese Art von Bindung als Elektronenpaarbindung. Je
stärker der räumliche Überlapp der Wellenfunktionen, desto
stärker die kovalente Bindung. (Weiteres Beispiel: Zwei sich
annähernde, unendlich hohe Rechteck–Potentialtöpfe mit je
einem Elektron, eindimensional.)
Die kovalente Bindung braucht zu ihrer Realisierung
unvollständig besetzte Einzelatomorbitale. Diamant zum
Beispiel besitzt die Konfiguration 1s2, 2s2, 2p2; es stehen also
nur die beiden p–Orbitale der kovalenten Bindung zur
Verfügung. Man findet aber vier kovalente Bindungen. Die
Erklärung liefert die sog. Hybridisierung (zur Erinnerung:
CH4–Molekül). Unter dem Einfluss der Nachbarn wird
der kleine energetische Unterschied zwischen 2s2– und
2p2–Orbitalen wieder aufgehoben. Aus den Wellenfunktionen
2s, 2px, 2py und 2pz werden vier neue Linearkombinationen
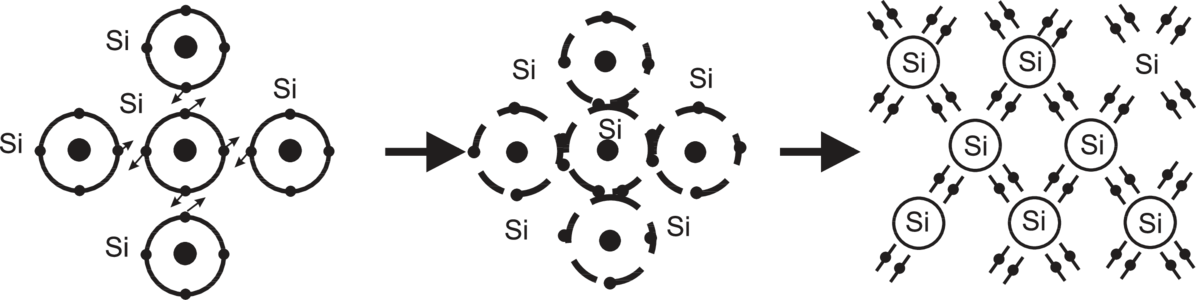
gebildet: Die sp3–Hybrid–Orbitale bilden im Raum einen
perfekten Tetraeder aus (109, 5° – Winkel). Ordnen sich im
periodischen Gitter der Festkörper die nächsten Nachbarn
jeweils gerade auf den Tetraederpositionen an, so kommt es
zur Ausbildung von 4 kovalenten Bindungen pro Atom.
D. h. die Nachbaratome teilen sich die verfügbaren Elektronen
gerade so, dass nur die bindenden Zustände besetzt sind.
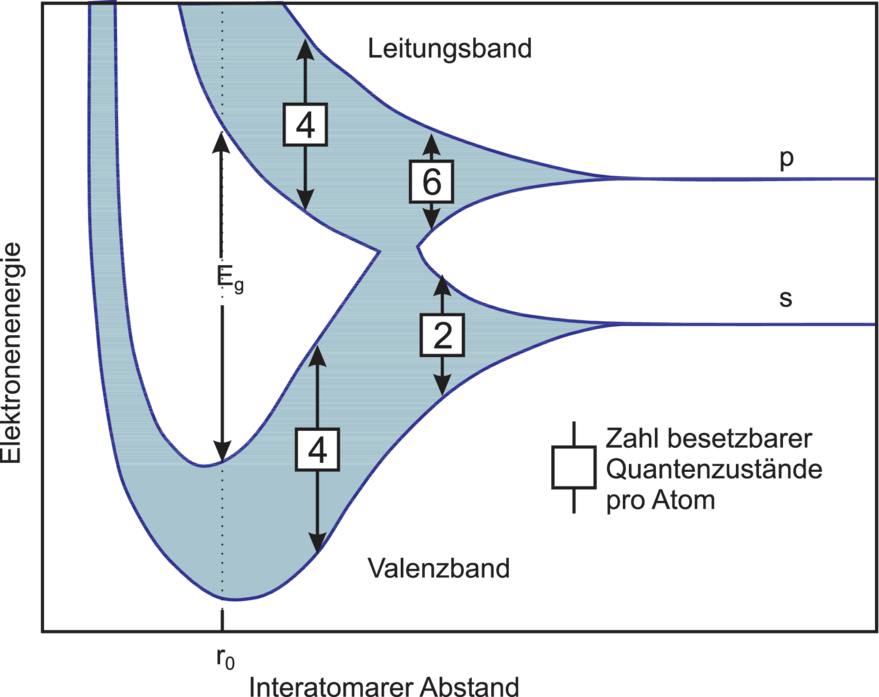
Abbildung 3.2 gibt das wieder: die s– und p–Orbitale
spalten bei Annäherung der Atome auf, dann aber bilden
sich die — ebenfalls aufgespaltenen — Hybridorbitale
aus.
Mit kleiner werdendem Atomabstand entsteht eine
verbotene Zone, d. h. zwischen bindenden und antibindenden
sp3–Teilbändern tut sich ein ‘Gap’ auf. Alle vier pro Atom zur
Verfügung stehenden Elektronen haben im tiefer liegenden,
bindenden Band, dem sog. Valenzband, Platz: es liegt bei
T = 0K ein Isolator vor. Abbildung 3.2 gilt für kristalline und
amorphe Elementhalbleiter gleichermassen, solange die
tetraedrische Bindungsanordnung vollständig gegeben ist;
allerdings führen die im Amorphen etwas variierenden
Abstände und das Vorhandensein von unabgesättigten
Bindungen zu Abweichungen: es gibt Zustände, die die
Energielücke verkleinern. Ergänzend sei bemerkt, dass
mit dem temperaturabhängigen Atomabstand auch die
Energiebreiten der Bandlücke temperaturabhängig sein muss:
bei T = 0K ist sie am grössten.
Die oben besprochene räumliche Struktur der kovalenten
Bindung wird gerne in eine zweidimensionale, abstrakte
Darstellung (‘Bindungsmodell’) überführt, um z. B. die
elektrische Leitung zu veranschaulichen.
Die sp3–Hybridisierung findet man bei den III–V–Halbleitern
wieder. Es liegt eine Mischbindung aus ionischer Bindung
(Ladungstransfer vom V er– zum III er–Material) und
kovalenter Bindung vor; letztere überwiegt. Auch die
II–VI–Halbleiter zeigen diese Mischbindung, mit grösserem
ionischen Anteil als die III–V- er.
Bisher betonten wir die physikalischen Gemeinsamkeiten.
Die unterschiedlichen atomaren Eigenschaften spiegeln sich in
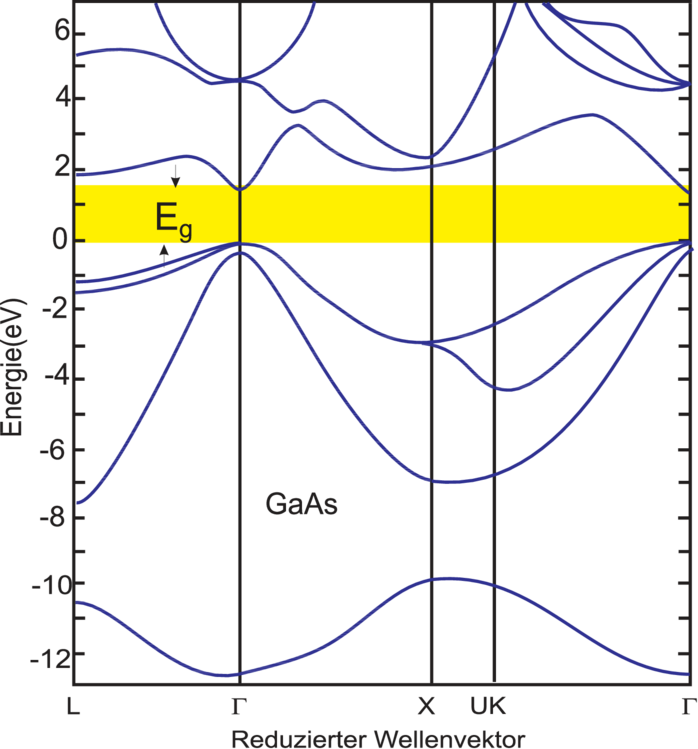
unterschiedlichen Bandstrukturen wieder. Im Abbildung 3.4
sind die E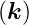 –Darstellungen der elektronischen Bänder aus
(an Experimente angepasste) Rechnungen für Si, Ge
und GaAs angegeben. (Weiterführende Arbeiten zeigen
noch kompliziertere Band–Feinstrukturen, z. B. führt die
Berücksichtigung der Spin–Bahn–Aufspaltung bei Si und Ge
zur Aufspaltung der Oberkante des Valenzbandes, es gibt
dann leichte, schwere und ‘split–off’–Löcher.)
–Darstellungen der elektronischen Bänder aus
(an Experimente angepasste) Rechnungen für Si, Ge
und GaAs angegeben. (Weiterführende Arbeiten zeigen
noch kompliziertere Band–Feinstrukturen, z. B. führt die
Berücksichtigung der Spin–Bahn–Aufspaltung bei Si und Ge
zur Aufspaltung der Oberkante des Valenzbandes, es gibt
dann leichte, schwere und ‘split–off’–Löcher.)
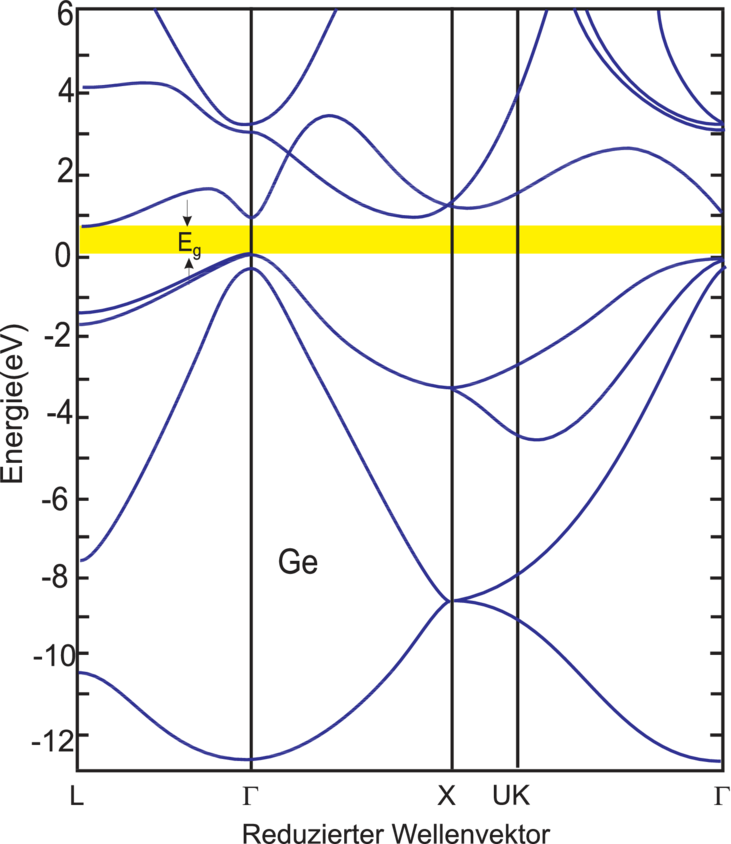
Si und Ge sind sog. indirekte Halbleiter. Das Maximum der
Valenzband–Oberkante liegt beidesmal beim Γ–Punkt
(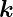 =
= 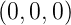 ), aber das Minimum der Leitungsband–Unterkante
liegt bei Si am X–Punkt (ΓX=[100]–Richtung) und bei Ge am
L–Punkt (ΓL=[111]–Richtung). Auch GaP und AlSb
haben eine indirekte Bandlücke. Aber die wichtigsten
III–V–Halbleiter (GaAs, GaSb, InSb, InAs, InP) haben
eine direkte Bandlücke, d. h. Valenzbandmaximum und
Leitungsbandminimum liegen beide bei Γ; gleiches gilt für
die II–VI–Halbleiter ZnO, ZnS, CdS, CdSe und CdTe.
Man spricht von direkten Halbleitern. Auf Halbleitern
mit direkter Bandlücke basieren die optoelektrischen
Bauelemente.
), aber das Minimum der Leitungsband–Unterkante
liegt bei Si am X–Punkt (ΓX=[100]–Richtung) und bei Ge am
L–Punkt (ΓL=[111]–Richtung). Auch GaP und AlSb
haben eine indirekte Bandlücke. Aber die wichtigsten
III–V–Halbleiter (GaAs, GaSb, InSb, InAs, InP) haben
eine direkte Bandlücke, d. h. Valenzbandmaximum und
Leitungsbandminimum liegen beide bei Γ; gleiches gilt für
die II–VI–Halbleiter ZnO, ZnS, CdS, CdSe und CdTe.
Man spricht von direkten Halbleitern. Auf Halbleitern
mit direkter Bandlücke basieren die optoelektrischen
Bauelemente.
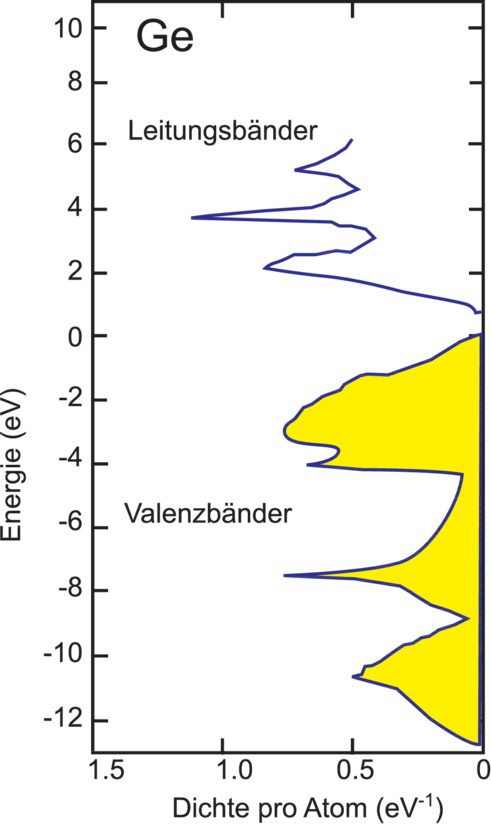
Der Vollständigkeit halber ist für Ge die theoretisch
ermittelte elektronische Zustandsdichte D(E) wiedergegeben,
dabei sind die besetzten Zustände der Valenzbänder
schraffiert worden. Einige kritische Punkte lassen sich auf
Minima oder Maxima in der Bandstruktur zurückführen. Von
den komplizierten Verläufen darf man sich nicht abschrecken
lassen, für die elektrische Leitfähigkeit genügt es i. allg. den
Verlauf des Valenz– und des Leitungsbands rund um Γ zu
kennen.
3.1.2 Intrinsischer Halbleiter
Bei T = 0K zeigen Halbleiter keine Leitfähigkeit. Bei
endlichen Temperaturen aber kommt es zu einer ‘thermischen
Anregung’ von Elektronen über die Bandlücke hinweg. Sie
hinterlassen im Valenzband jeweils eine positiv geladene
Lücke, ein sog. Loch. In einem äusseren elektrischen Feld 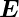 können nicht nur die Elektronen im Leitungsband (wie bei
den Metallen) Energie aufnehmen, sondern auch die im
Valenzband. Vereinfachend wird dies beschrieben durch die
Energieaufnahme der Löcher.
können nicht nur die Elektronen im Leitungsband (wie bei
den Metallen) Energie aufnehmen, sondern auch die im
Valenzband. Vereinfachend wird dies beschrieben durch die
Energieaufnahme der Löcher.
Für die Stromdichte gilt (im stationären Fall) bei Metallen:
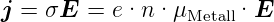 | (3.1) |
und für die elektrische Leitfähigkeit
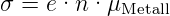 | (3.2) |
mit μ als Beweglichkeit und n als Anzahldichte der
Elektronen.
Für die Leitfähigkeit bzw. für die Beweglichkeit bei
Halbleitern gilt analog:
Im allg. gilt für die Beweglichkeit der Elektronen μn
und der Löcher μp die Relation μn > μp > μMetall; n
und p sind die Volumenanzahldichten der Elektronen
bzw. Löcher. Letztere zeigen, im Gegensatz zu μMetall, eine
starke Temperaturabhängigkeit. Ein intrinsischer Halbleiter
ist gekennzeichnet durch das blosse Vorhandensein des oben
beschriebenen thermischen Anregungsmechanismus. Man
spricht auch vom idealen Halbleiter, weil Störstellen–freien
Halbleiter. Wir haben also zwei Ladungsträgertypen im
Halbleiter! Im thermodynamischen Gleichgewicht werden
sie ständig generiert und rekombinieren — nach einer
Lebensdauer τ — wieder ins Valenzband.
Die Beweglichkeiten μn und μp sind — was in der obigen
Gleichung nicht enthalten ist — streng genommen Impuls–
bzw. Energie–abhängige Grössen. Häufig genügt es jedoch
völlig, die Ladungsträger in den Valenzbandmaxima und
Leitungsbandminima zu berücksichtigen, d. h. nicht zu
grosse T und 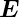 zuzulassen. Dann gilt für die betrachteten
Bänder die sog. parabolische Näherung (auch Näherung der
Standardbänder):
zuzulassen. Dann gilt für die betrachteten
Bänder die sog. parabolische Näherung (auch Näherung der
Standardbänder):
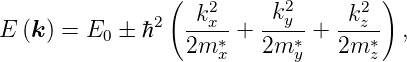 | (3.5) |
mit m∗ als konstante, d. h. Impuls– bzw. Energie–unabhängige
effektive Masse (‘effektive Massennäherung’).
Für die tensorielle effektive Masse mij∗ gilt:
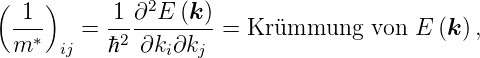 | (3.6) |
ein kleines m∗ beschreibt also eine starke Bandkrümmung, ein
grosses m∗ eine schwache.
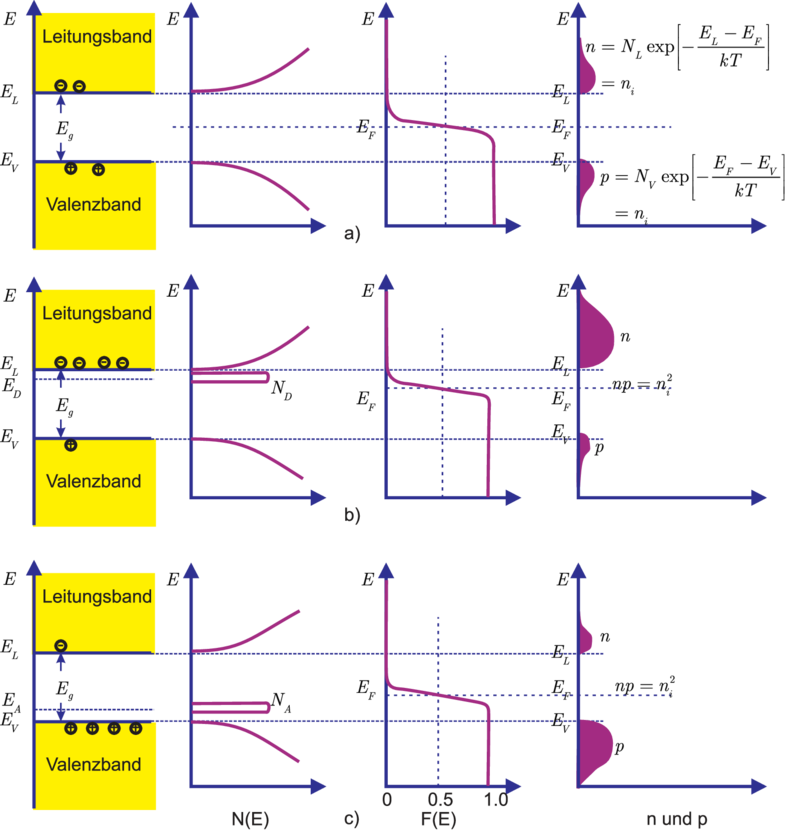
Für die Dichten der Ladungsträger in Leitungs– und
Valenzband gilt ganz allgemein:
mit EL bzw. EV als Energien der Leitungsbandunterkante
bzw. Leitungsbandoberkante, DL und DV als Zustandsdichten
der Elektronen und Löcher und mit f als Verteilungsfunktion
gemäss der Fermistatistik mit EF, der Fermieenergie als
chemischem Potential, also
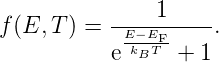 | (3.9) |
Für die Zustandsdichten gilt in parabolischer Näherung:
Die sog. Neutralisationsbedingung des Idealhalbleiters
ergibt sich aus der thermischen Anregung, die Generation
eines Elektrons ins Leitungsband erzeugt ein Loch im
Valenzband:
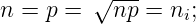 | (3.13) |
ni steht für Inversionsdichte, auch Eigenleitungskonzentration
genannt; analog dazu bezeichnet man σi als Eigenleitung.
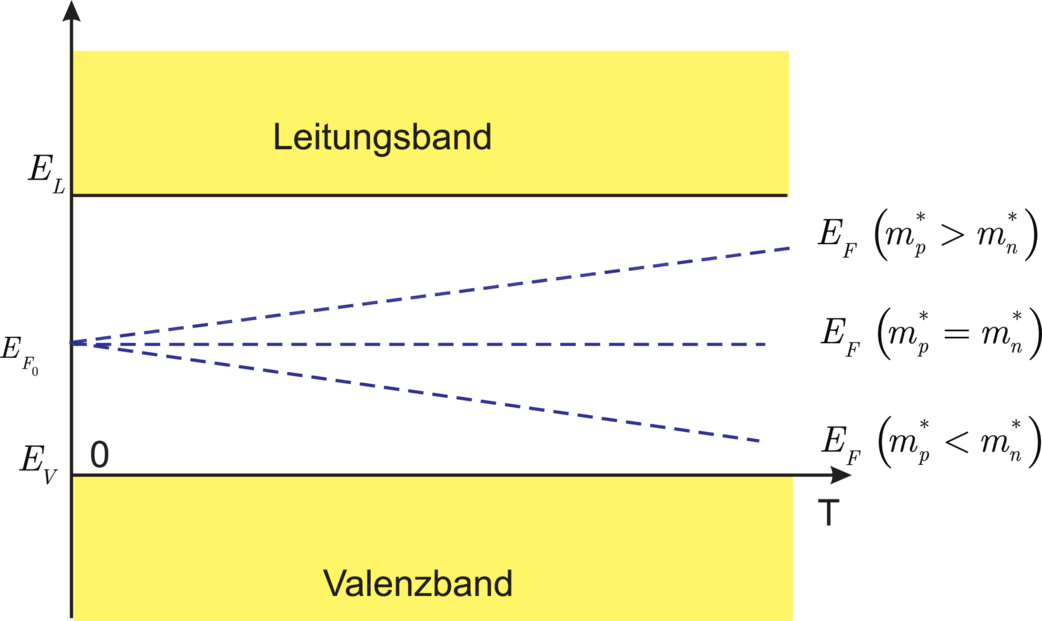
Wenn die effektiven Massen mn∗ und m
p∗ gleich sind, also
auch die Zustandsdichten gleich sind, muss das Fermi–Niveau
EF in der Mitte der Bandlücke liegen. Bei ungleichen Massen
wandert das Fermi–Niveau aus der Mitte, seine Lage ist
dann schwach temperaturabhängig. (Konsequenzen für
elektronische Bauelemente!)
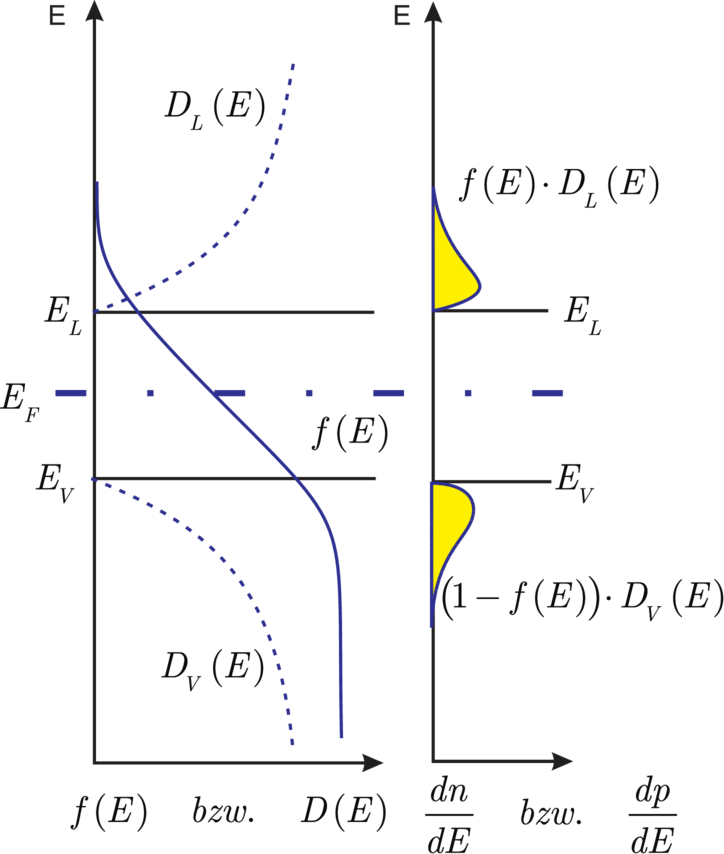
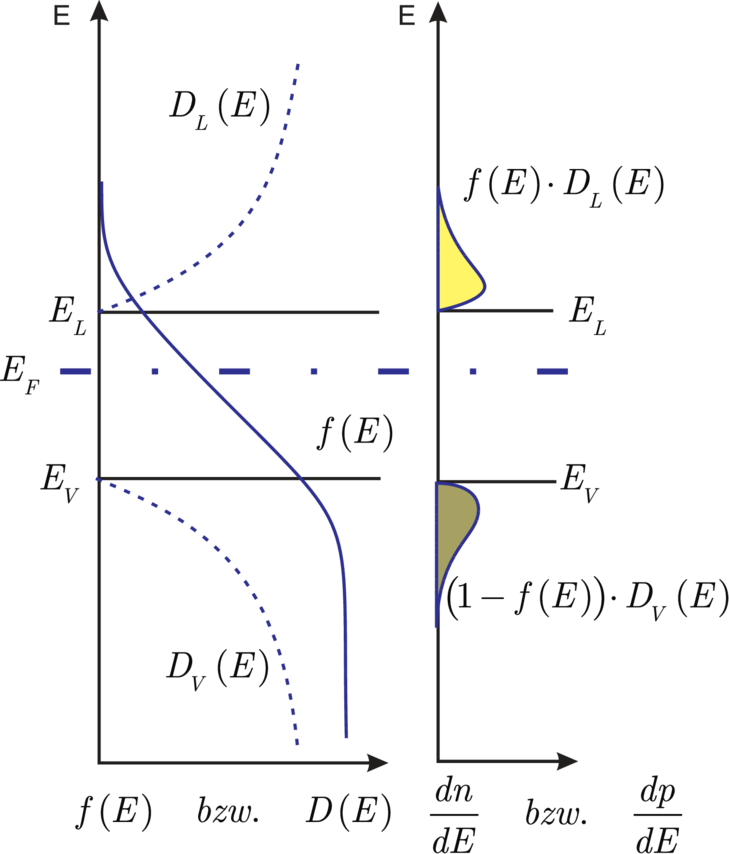
Man sieht im linken Teilbild von 3.5, dass nur die
‘Ausläufer’ der Fermifunktion bei der Berechnung der
Ladungsträgerkonzentrationen (zum Produkt für D) beitragen.
Die ‘Aufweichungszone’ der Fermifunktion (≈ 2kBT) ist bei
Raumtemperatur klein: kBT ≈ 25meV = 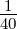 eV. Die Energielücke
ist — bis auf ein paar wenige Ausnahmen (α–Sn, InSb)
10–100 mal grösser. Man darf deshalb die Fermifunktion
durch die Boltzmann–Besetzungswahrscheinlichkeit annähern:
eV. Die Energielücke
ist — bis auf ein paar wenige Ausnahmen (α–Sn, InSb)
10–100 mal grösser. Man darf deshalb die Fermifunktion
durch die Boltzmann–Besetzungswahrscheinlichkeit annähern:
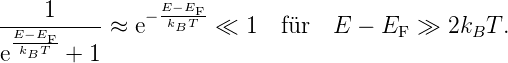 | (3.14) |
Diese Näherung nennt man die Näherung der Nichtentartung,
sie ist gut für kleine Ladungsträgerkonzentrationen. Für diese
liefert dann die Rechnung:
Die sog. effektiven Zustandsdichten (auch
Entartungskonzentrationen) NeffL,V gelten also formal für ein
einziges Energieniveau, nämlich die Bandkante L, V.
Damit lässt sich die Neutralisationsbedingung in der Form
eines Massenwirkungsgesetzes schreiben:
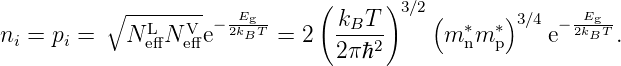 | (3.17) |
Aus diesem Grund nennt man die Halbleiter ‘Heissleiter’
(und Metalle im Vergleich hierzu Kaltleiter). Weiter gilt:
In Tabelle 3.1 sind zum Abschluss einige Zahlenwerte für die
Inversionsdichte ni bei 300K angegeben. Diese Werte sind
in Relation zu sehen mit typischen Atomdichten von
> 2−< 5·1022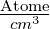 .
.
| | ni[cm−3] |
|
|
| C | 6, 7·10−28 |
| Si | 1, 5·1010 |
| Ge | 2, 4·1013 |
| GaAs | 5·107 |
| Tabelle 3.1.: | Inversionsdichten ni einiger Materialien bei
Raumtemperatur. |
Die experimentelle Beobachtbarkeit der intrinsischen
Leitung setzt extrem sauberes Halbleiter–Material voraus. Die
niedrigsten erreichbaren Verunreinigungskonzentrationen bei
Halbleitereinkristallen wie Ge und Si liegen bei etwa
1012cm−3. (Vergleiche tiegelfreies Zonenziehen und
Zonenreinigen von Siliziumstäben; Si ist der am reinsten
darstellbare Stoff überhaupt.) Reinstes GaAs dagegen hat
heute Ladungsträgerdichten von 1016cm−3.
Extrem reines Material ist bei Raumtemperatur
sehr hochohmig (siehe Beispiel Si); der Transport von
elektrischem Strom ist also sehr verlustreich. Deshalb werden
gezielt elektrisch aktive Störstellen in den Halbleiter
eingebaut. Erst die Möglichkeit, definiert räumliche
Konzentrationsprofile von freien Elektronen und freien
Löchern auf sub–μm–Skala vorgeben zu können, ermöglicht
die moderne Festkörperelektronik.
3.1.3 Dotierung von Halbleitern
Verunreinigt man Si (oder Ge) gezielt mit fünfwertigen
Atomen wie P, As oder Sb, so beobachtet man bei endlichen
Temperaturen eine erhöhte Ladungsträgerdichte im
Leitungsband. Diese Störstellen heissen dann Donatoren, der
so dotierte Halbleiter heisst n–Halbleiter.
Baut man in vierwertige Halbleiter–Materialien dreiwertige
Fremdatome wie B, Al, Ge oder In ein, so findet man bei
T > 0K eine erhöhte Ladungsträgerdichte im Valenzband.
Solche Störstellen werden als Akzeptoren bezeichnet; in
Analogie spricht man von p–Halbleitern.
Abbildung 3.7 zeigt schematisch den Einbau eines Donator–
bzw. Akzeptoratoms auf einem Gitterplatz im Si–Einkristall.
Im Falle des Donators nehmen vier Valenzelektronen an den
kovalenten Bindungen zu den benachbarten Si–Atomen teil,
das fünfte Elektron ist nur schwach an das Phosphoratom
gebunden und kann schon bei kleinen Temperaturen
angeregt bzw. ionisiert (T ≥ 10K), also ins Leitungsband
angehoben werden. Analog gilt für ein Akzeptoratom,
dass schon bei kleinen Temperaturen ein Elektron aus
dem Valenzband die kovalente Bindung komplettieren
kann und so ein schwach gebundenes Loch bzw. durch
Ionisation ein zusätzliches freies Loch im Valenzband erzeugt
wird.
Der Radius der Störstellenbahn beträgt ca. 10 Gitterabstände
bzw. das schwach gebundene Elektron bzw. Loch
ist über ca. 103 Si–Gitteratome ‘verschmiert’. Aus
FIR–Absorptionsspektroskopie–Experimenten bei tiefen
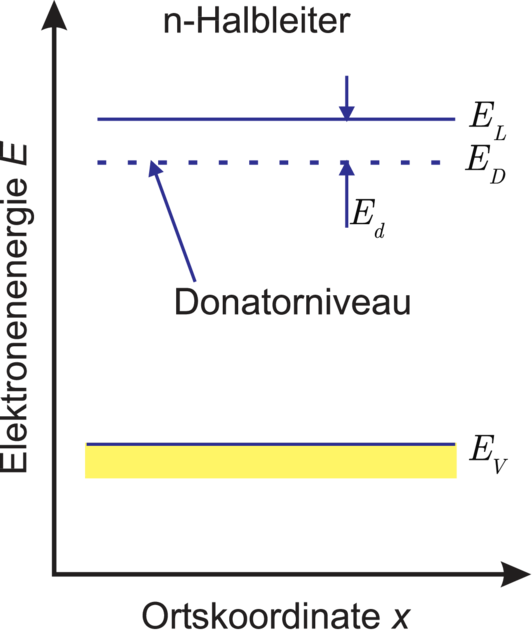
Temperaturen kennt man die energetischen Abstände ED
der Donatorniveaus bzw. EA der Akzeptorniveaus vom
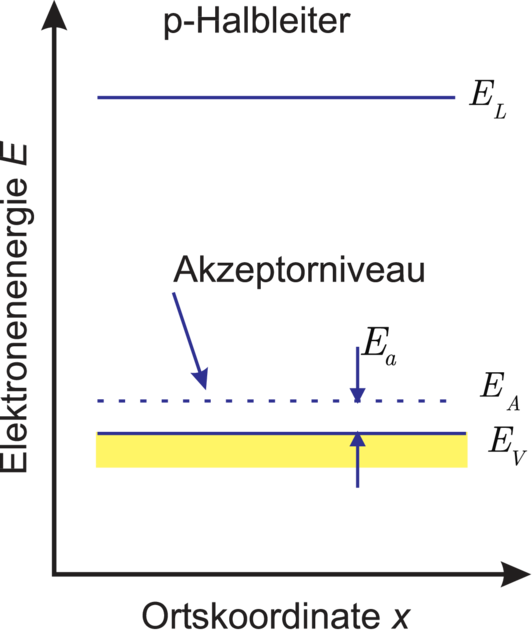
Leitungsband bzw. Valenzband. Dies geben qualitativ
die beiden in Abbildung 3.8 gezeigten Bändermodelle
(Valenzbandmaximum und Leitungsbandminimum über
Ortskoordinate, ergänzt um die Störstellen–Grundniveaus)
wieder.
Die aus den genannten Absorptionsspektren bekannten
angeregten Niveaus sind nicht eingezeichnet. Zur Abschätzung
der Anregungs– und Ionisationsenergien, sowie der
Ausdehnung von Störstellen kann ein Wasserstoffatom–Modell
herangezogen werden. (me wird ersetzt durch m∗, 𝜖
0 durch
𝜖0·𝜖Si, 𝜖Si = 11, 7 (Abschirmung der Coulomb–Anziehung
zwischen P+ und e− bzw. B− und positiv geladenem Loch)).
Im Vergleich zu den Bandlücken sind die Störstellenabstände
i. allg. klein (‘flache Störstellen’), tiefer sitzende Störstellen
sind schwerer bzw. praktisch gar nicht thermisch zu
ionisieren und erhöhen die Ladungsträgerdichten nicht.
Als Beispiel sind in den Tabellen 3.2 und 3.3 einige wichtige
Messwerte angegeben.
| | P [meV] | As [meV] | Sb [meV] |
|
|
|
|
| Si | 45 | 54 | 43 |
| Ge | 13 | 14 | 10 |
| Tabelle 3.2.: | Energetischer
Abstand ED einiger Donatorenniveaus vom Leitungsband
für Silizium und Germanium[IL99]. |
| | B [meV] | Al [meV] | Ga [meV] | In [meV] |
|
|
|
|
|
| Si | 45 | 67 | 74 | 153 |
| Ge | 11 | 11 | 11 | 12 |
| Tabelle 3.3.: | Energetischer Abstand
EA einiger Akzeptorniveaus vom Valenzband für Silizium
und Germanium[IL99]. |
Der Eigenhalbleiter hat im thermodynamischen
Gleichgewicht immer die gleiche Konzentration an Elektronen
und an Löchern. Im gezielt dotierten Material ist dies
anders. Im Falle der n–Dotierung befinden sich mehr
Elektronen im Leitungsband als Löcher im Valenzband. Die
Elektronen sind also die sog. Majoritätsladungsträger
und die Löcher die sog. Minoritätsladungsträger. Es
gilt:
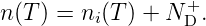 | (3.20) |
ND+ (N
A−) ist die Anzahldichte der ionisierten Donatoren
(Akzeptoren). Für den Fall der p–Dotierung gilt für die
Majoritätsladungsträger analog:
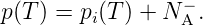 | (3.21) |
Auch im dotierten Halbleiter gilt (im thermodynamischen
Gleichgewicht) die grundlegende Beziehung:
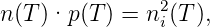 | (3.22) |
d. h. eine Erhöhung von n(T) bewirkt eine Erniedrigung
von p(T) um denselben Faktor! I. allg. sind die
Minoritätsladungsträger–Anzahldichten sehr klein im
Vergleich zu denen der Majoritätsladungsträger; im
homogenen Halbleiter sind sie praktisch vernachlässigbar, in
Bauelementen mit ihren inhomogenen Dotierungen, Grenz–
und Randschichten aber keinesfalls.
3.1.4 Ladungsträgerdichten im dotierten Halbleiter
Solange die Besetzung im Leitungsband bzw. im Valenzband
in guter Näherung mit Hilfe der Boltzmann–Verteilung
beschrieben werden kann (Fall des nicht entarteten Halbleiters),
gilt auch für dotierte Halbleiter das Massenwirkungsgesetz:
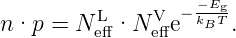 | (3.23) |
Eine etwas kompliziertere Neutralitätsbedingung regelt
wieder die Lage des Fermi–Niveaus EF im homogen dotierten
Halbleiter; die negative Ladungsträgerdichte muss gleich der
positiven Ladungsträgerdichte sein:
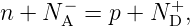 | (3.24) |
wobei für die Störstellendichte gilt:
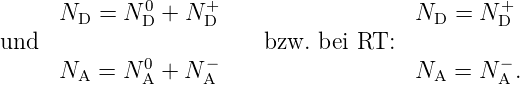 | (3.25) |
ND,A0 bezeichnt dabei die Anzahldichte der nicht ionisierten
Donatoren bzw. Akzeptoren. Für Störstellenkonzentrationen
von ≥ 1017cm−3, wie sie für p– bzw. n–Dotierung üblich sind,
nicht aber für ‘hohe Dotierungen’ p+ oder n+ (1018cm−3), gilt
in guter Näherung:
Der allgemeine Fall, wo gleichzeitig p– und n–Dotierung
vorliegt, ist nur numerisch lösbar, reine n– oder p–Dotierung
kann (mit den oben angegebenen Formeln) diskutiert werden.
Für die n–Dotierung lautet die Lösung:
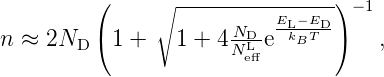 | (3.28) |
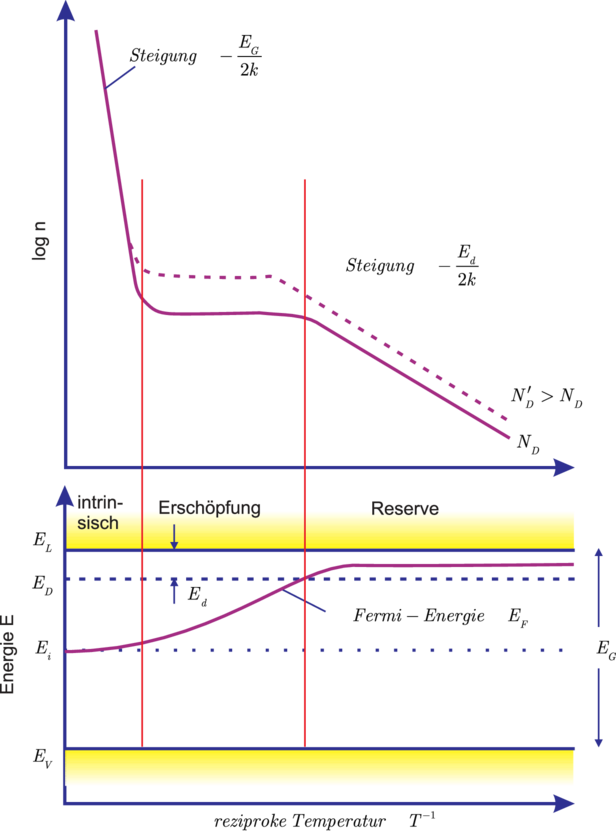
sie beschreibt für kleine Temperaturen das Regime der
Störstellenreserve, dann den Erschöpfungszustand (der
Donatoren) und für hohe Temperaturen den Bereich der
intrinsischen Trägerkonzentration. Die Lage der Fermi-Energie
verhält sich entsprechend: für T = 0K liegt sie in der Mitte
zwischen ED und der Leitungsbandunterkante EL, reicht im
mittleren Temperaturbereich von EL weg und endet im
intrinsischen Bereich in der Mitte zwischen ED und EV, also
auf Ei.
Die experimentelle Bestimmung der Ladungsträgerdichten
in Abhängigkeit von der Temperatur geschieht unter
Benutzung des Hall–Effekts.
Bei Dotierungskonzentrationen z. B. von ≥ 1017cm−3 bei
Si (n+ bzw. p+) erreicht bzw. überschreitet man die
sog. kritische Konzentration: die Donatoren bzw. Akzeptoren
‘sehen’ einander. Angeregte Störstellen–Zustände liegen unter
EL oder über EV und die Energielücke des Halbleiters wird
um einige 10meV kleiner, gleichzeitig werden weniger
Störatome ionisiert, als es bei der entsprechenden Temperatur
zu erwarten wäre.
3.1.5 Leitfähigkeit in Abhängigkeit von Dotierkonzentration
und Temperatur
Im Gegensatz zu den Metallen tragen bei den Halbleitern
nicht nur Elektronen an der Fermi–Kante zur elektrischen
Leitfähigkeit bei, sondern es müssen die von Elektronen
bzw. Löcher besetzten Zustände im unteren Leitungsband
bzw. oberen Valenzband berücksichtigt werden. Deshalb sind
Grössen wie die Beweglichkeiten μn und μp immer als
Mittelwerte aufzufassen, die auch vom elektrischen Feld 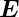 abhängen können; die folgenden Aussagen gelten für relativ
kleine Feldstärken.
abhängen können; die folgenden Aussagen gelten für relativ
kleine Feldstärken.
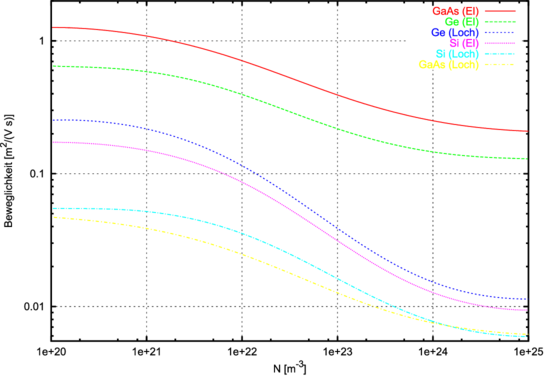
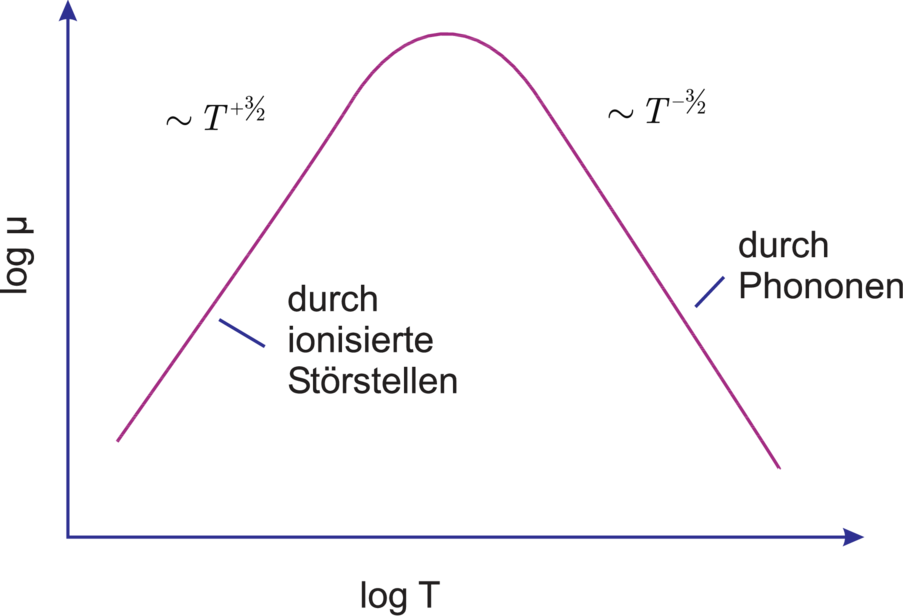
Ohne Diskussion von Details bleibt festzuhalten, dass die
Ladungsträger zum einen hauptsächlich an akustischen
Phononen und andererseits an gebundenen Störstellen
(ionisierte Donatoren und Akzeptoren) gestreut werden. Bei
niedrigen Dotierkonzentrationen beobachtet man den
temperaturabhängigen Einfluss der Phononen, bei hohen
Dotierkonzentrationen ist die Temperaturabhängigkeit sehr
klein und die Beweglichkeit ist um 1–2 Grössenordnungen
verringert.
Die Diskussion der Temperaturabhängigkeit der
Leitfähigkeits–Messkurven ist noch etwas schwieriger,
denn zur T–Abhängigkeit der Beweglichkeiten ist die der
Trägerkonzentrationen zusätzlich zu bedenken.
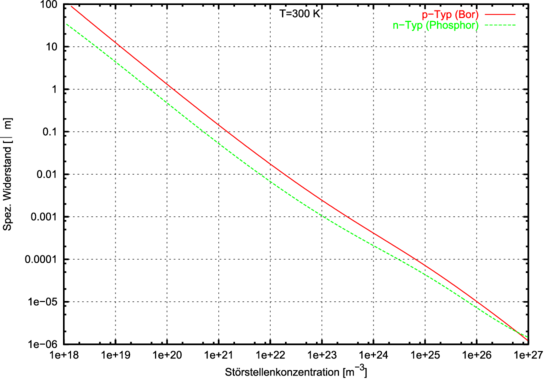
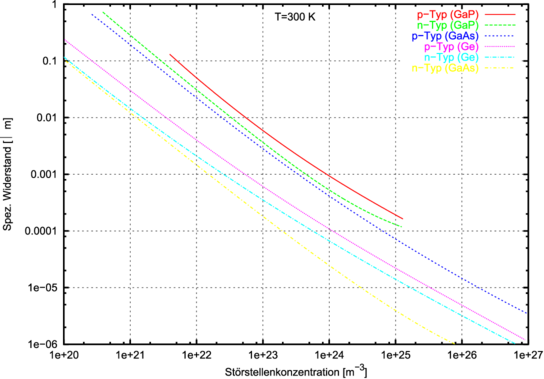
Sehr viel einfacher dagegen sind die Widerstands–Konzentrationskurven,
sie spiegeln einen eindeutigen Zusammenhang wieder. Wer
eine ordentliche 4–Spitzen–Messung des Widerstands
durchführt, kann bei bekanntem Dotierungstyp auf die
Dotierungskonzentration rückschliessen.
Das ohmsche Verhalten der Leitfähigkeit von Halbleitern
gilt bis zu Feldstärken von typischerweise 103 – 104V∕cm
(materialabhängig). In den aktuellen Halbleiter–Bauelementen
mit Submikrometer–grossen Inhomogenitäten im Aufbau
können Feldstärke–Werte von 105 – 106V∕cm auftreten. Die
Driftgeschwindigkeit erreicht bei Silizium (Löcher und
Elektronen) einen Sättigungswert von 107cm∕s, wobei vor
allem die Wechselwirkung der Ladungsträger mit den
optischen Phononen hierfür verantwortlich ist. (Diese
Sättigungswerte sind höher als die des GaAs; allerdings zeigen
GaN, GaAs und InP bei kleineren Feldstärken ein deutlich
höher liegendes Maximum in vD(E).
3.1.6 Rekombinationsprozesse und Ladungsträgertransport:
Grundgleichungen zur Funktion von Halbleiter–Bauelementen
Wenn in einem physikalischen System die Bedingung des
thermischen Gleichgewichts verletzt ist, gibt es stets Prozesse,
die das System wieder ins Gleichgewicht zurück bringen. Wird
beispielsweise (in einem beliebig dotierten Halbleiter) durch
optische Anregung lokal die Ladungsträgerdichte erhöht, so
dass p·n ⇔ ni2 gilt, so relaxiert sie am Ende wieder zu
p·n = ni2. Im Halbleiter geschieht dies, anders als im Metall,
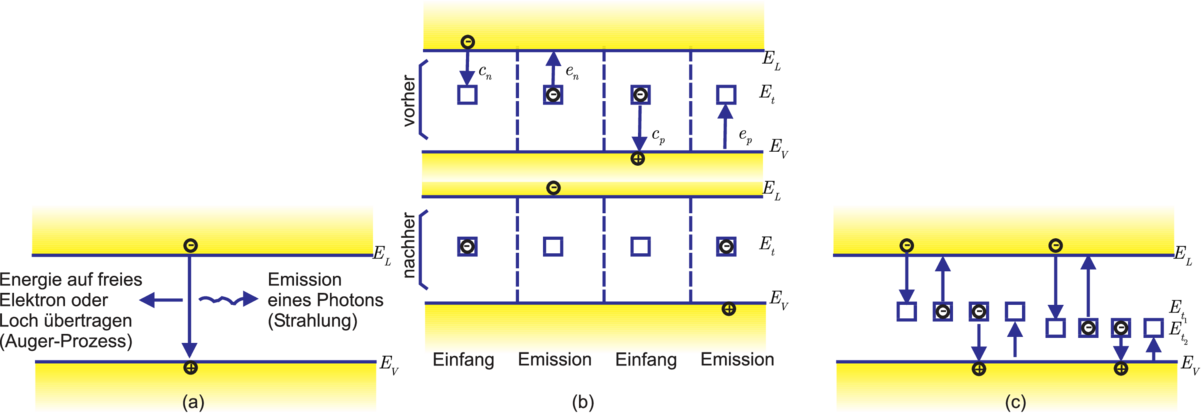
wesentlich durch die sog. Rekombinationsprozesse. Abbildung
3.14 gibt die grundlegenden Rekombinationsprozesse der
Halbleiter wieder.
In Abbildung 3.14 (a) ist die sog. Elektron–Loch–Rekombination
gezeigt: das Elektron macht eine Band–Band–Rekombination,
die Übergangsenergie wird an ein Photon (‘strahlender
Rekombinationsprozess’), wichtigster Prozess bei direkten
Halbleitern, oder an ein freies Elektron im Leitungsband
bzw. an ein freies Loch im Valenzband (’nichtstrahlender
Rekombinationsprozess’) abgegeben.
Im weiteren werden die für indirekte Halbleiter wie
Si so wichtigen Störstellen–Rekombinationsprozesse
aufgezeigt. Eine tiefe Störstelle in (b), vereinfacht mit einem
einzigen Energieniveau angenommen, kann Elektronen
bzw. Löcher ‘trappen’ und wieder freisetzen; verschiedene
Störstellen mit mehreren Energieniveaus besitzen noch mehr
Rekombinationsmöglichkeiten (c).
Besonders effektiv wirken Störstellen in der Mitte der
Bandlücke. (Deshalb sind Au– oder Cu–Verunreinigungen
im Si i. allg. gefürchtet.) Gezielt eindiffundierte tiefe
Störstellenatome, hochenergetische elektromagnetische
Strahlung und energiereiche Partikelstrahlung ermöglichen es,
die Rekombinationsraten lokal kontrolliert zu erhöhen. Meist
muss man aber tiefe Traps unbedingt vermeiden.
Die Umkehr der Rekombinationsprozesse von Teilbild (a),
nämlich der direkte optische Übergang (bei direkten Halbleiter
wie GaAs) bzw. die Stossionisation (von Elektronen im
Valenzband) bei hohen elektrischen Feldern geben zwei Wege
zur Erzeugung zusätzlicher Ladungsträger im thermischen
Nichtgleichgewicht an.
Die lokal erhöhte Elektronen– bzw. Löcherkonzentration
zerfällt räumlich durch Diffusion (aufgrund der zufälligen
thermischen Bewegung der Ladungsträger) und zeitlich durch
die oben eingeführten Rekombinationsprozesse.
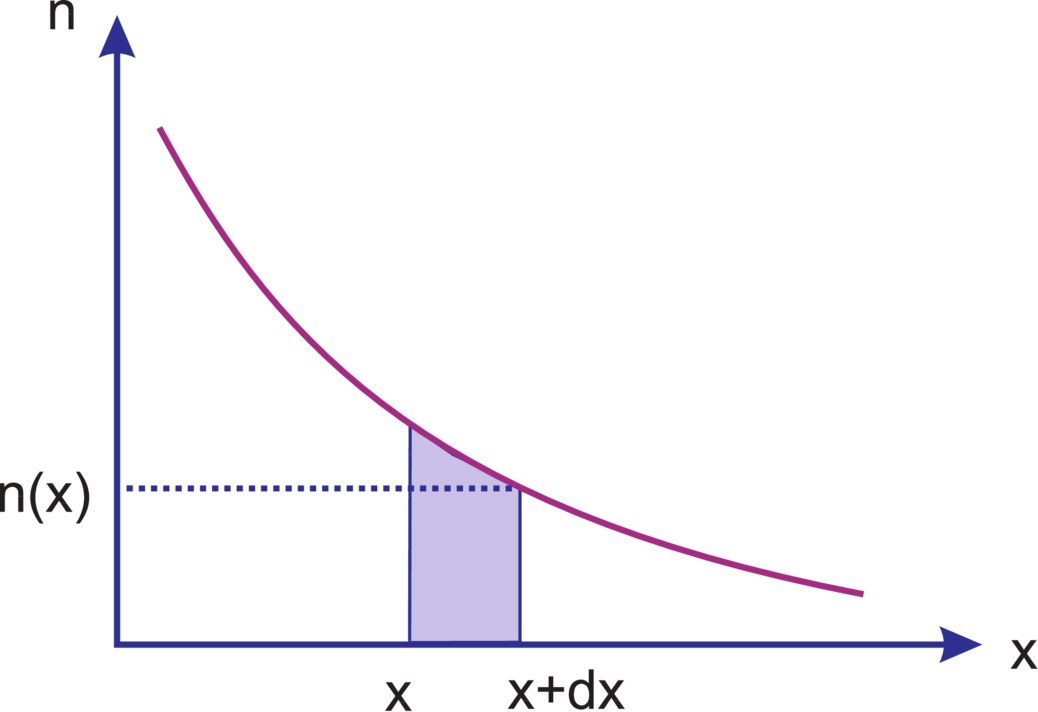
Der Strom von Elektronen, der in der Abbildung
3.15 von links den Ort x erreicht, wird aufgrund der
vorhandenen Rekombinationsprozesse im Wegintervall
dx um den Betrag djn geschwächt. Immer wenn in
Halbleiter–Bauelementen Distanzen vergleichbar oder
grösser als die sog. Diffusionslängen der Elektronen oder
der der Löcher (Ln = 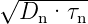 bzw. Lp =
bzw. Lp = 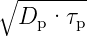 )
sind, verändert die Rekombination entlang des Wegs die
Stromdiche der Elektronen oder Löcher. Die entsprechenden
Diffusionslängen in Si und Ge betragen ca. 10mm. (Die in
GaAs ca. 0, 1mm.)
)
sind, verändert die Rekombination entlang des Wegs die
Stromdiche der Elektronen oder Löcher. Die entsprechenden
Diffusionslängen in Si und Ge betragen ca. 10mm. (Die in
GaAs ca. 0, 1mm.)
Zur Beschreibung von Si–Bauelementen darf die
für den intrinsischen Halbleiter in Kapitel 3.1.2
angegebene Driftstromdichte (drift current) um eine
Diffusionskomponente erweitert werden. Probleme mit
Ladungsträger–Konzentrationsgradienten werden so
behandelbar.
Die Volumenstromdichtengleichungen lauten:
mit Dn und Dp als Diffusionskonstanten (’diffusion
coefficient, diffusion constant’). Damit im Halbleitermaterial
im Gleichgewichtszustand Ladungsneutralität herrscht, muss
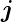 = 0 sein. Dies ist bei schwach dotierten Halbleitern die
einzige Bedingung. Bei stark dotierten Halbleitern jedoch
muss für die einzelnen Ladungsträgerarten
= 0 sein. Dies ist bei schwach dotierten Halbleitern die
einzige Bedingung. Bei stark dotierten Halbleitern jedoch
muss für die einzelnen Ladungsträgerarten 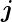 n = 0 und
n = 0 und 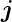 p = 0
gelten.
p = 0
gelten.
Nebenbemerkung:
Im Falle der nichtentarteten Halbleiter gilt die Einsteinrelation
Dn = 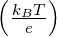 ·μn und Dp =
·μn und Dp = 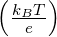 ·μp, die die Tatsache
wiedergeben, dass die Diffusion der Ladungsträger von ihrer
Beweglichkeit abhängt. Die angegeben Gleichungen enthalten
noch keine Magnetfeld–Effekte.
·μp, die die Tatsache
wiedergeben, dass die Diffusion der Ladungsträger von ihrer
Beweglichkeit abhängt. Die angegeben Gleichungen enthalten
noch keine Magnetfeld–Effekte.
Bei kleineren E–Feldstärken (in V/cm) gilt für den (für
Bauelemente besonders interessanten) eindimensionalen
Fall:
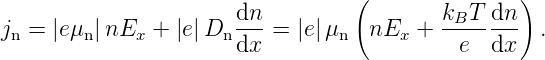 | (3.32) |
Für jp gilt die analoge Gleichung.
Unter äusserem Einfluss (optische Anregung, hohe
elektrische Felder) können im Halbleiter–Volumen also
lokal Elektronen und Löcher generiert werden: ‘excess
concentration of carriers’. Die zugehörigen Generationsraten
bezeichnen wir mit Gn und Gp (in cm3∕s). Analog führen wir
Rekombinationsraten Rn und Rp ein.
Die sog. Kontinuitätsgleichung lauten damit:
Im eindimensionalen Fall und unter der Bedingung, dass die
injizierte ladungsträgerdichte sehr viel kleiner als die
Majoritätsladungsträgerdichte ist (‘low injection condition’)
gilt:
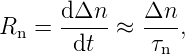 | (3.35) |
wobei Δn die Abweichung der Minoritätsladungsträgerdichte
vom thermodynamischen Gleichgewicht angibt; τn steht für
die Lebensdauer der (Minoritäts–) Elektronendichte. In
elektrisch neutralen Raumteilen gilt Δn = Δp.
Im eindimensionalen Fall gilt weiter:
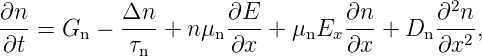 | (3.36) |
und analog
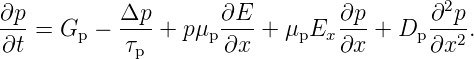 | (3.37) |
Einfache Beispiele für die Anwendbarkeit dieser Gleichungen
sind:
- n–Halbleiter unter Beleuchtung (Bestimmung der
Minoritätsladungsdauer nach Stevenson und Keyes).
Mit Δn ∼ e−t∕τ zerfällt nach dem Abschalten die
Nichtgleichgewichtskonzentration. Bei intrinsischen
Halbleitern sind die Lebensdauern typischerweise
> μs. Bei dotierten Halbleitern sind τn bzw. τp
stark von der Dotierkonzentration abhängig, die
Werte reichen von 1ns (bei 1021cm−3) bis 10μs (bei
1015cm−3) bei Si.
- Überschussladungsträger–Injektion von einer Seite
(Bestimmung der Diffusionslängen).
- Punktförmige optische Anregung mit und ohne
elektrisches Feld (Diffusionsexperiment nach Hayes
und Shockely).
- Oberflächen–Rekombination.
Die Tatsache, dass ein Halbleitereinkristall ein Ende hat,
bedeutet, dass er immer an dieser Oberfläche lokalisierte
Störstellen besitzt. Deren Dichte kann sehr gross sein
(ca. 1015cm−2). Energetisch liegen sie gerade zwischen E
V
und EL und damit bilden sie tiefe Oberflächenstörstellen
(‘surface trapping centers’). (Für vollkommen saubere
Oberflächen nennt man diese Oberfächenzustände nach ihrem
Entdecker Tamm–Zustände. Sie sind bedingt durch die
freien, unabgesättigten Valenzen der in ihrer Lage leicht
verschobenen Oberflächenatome. Gebundene Fremdatome
bewirken ebenfalls Störstellen mit allerdings deutlich
anderen Eigenschaften. Man trachtet immer danach,
diese zu vermeiden.) Die obigen Kontinuitätsgleichungen
sind entsprechend zu ergänzen, für Elektronen lautet
sie:
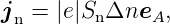 | (3.38) |
dabei wird 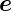 A als Einheitsnormalenvektor an der Oberfläche des
Halbleiters und Sn als Oberflächenrekombinations–Geschwindigkeit
(‘surface recombination velocity’) eingeführt. Die
Oberflächenrekombinations–Geschwindigkeit charakterisiert
jedes Interface, nur bei einer Dotierungsgrenzfläche (p–n oder
n–n+) ist sie vernachlässigbar. Abschliessend einige Zahlen:
A als Einheitsnormalenvektor an der Oberfläche des
Halbleiters und Sn als Oberflächenrekombinations–Geschwindigkeit
(‘surface recombination velocity’) eingeführt. Die
Oberflächenrekombinations–Geschwindigkeit charakterisiert
jedes Interface, nur bei einer Dotierungsgrenzfläche (p–n oder
n–n+) ist sie vernachlässigbar. Abschliessend einige Zahlen:
| für Metall–Halbleiter–Kontakte: | Sn ≈ 106cm∕s, |
| für Si–SiO2–Grenzflächen: | Sn ≈ 1cm∕s. |
Den wichtigen Anwendungsfall der Injektion durch
vorwärtsgespannte p–n–Übergänge behandeln wir später. (In
den Gleichungen Gleichung (3.36) und Gleichung (3.37) sind im
Falle der p–n–Diode die Grössen Δn durch Δnp und p durch
pn zu ersetzen, sprich Elektronen (Minoritätsladungsträger)
im p–Gebiet, Löcher (ebenfalls Minoritätsladungsträger) im
n–Gebiet.)
[Nächste Seite] [Vorherige Seite] [vorheriges Seitenende]
[Seitenanfang] [Ebene nach oben]
©2002-2017 Ulm
University, Othmar Marti,  Lizenzinformationen
Lizenzinformationen

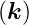 –Darstellungen der elektronischen Bänder aus
(an Experimente angepasste) Rechnungen für
–Darstellungen der elektronischen Bänder aus
(an Experimente angepasste) Rechnungen für 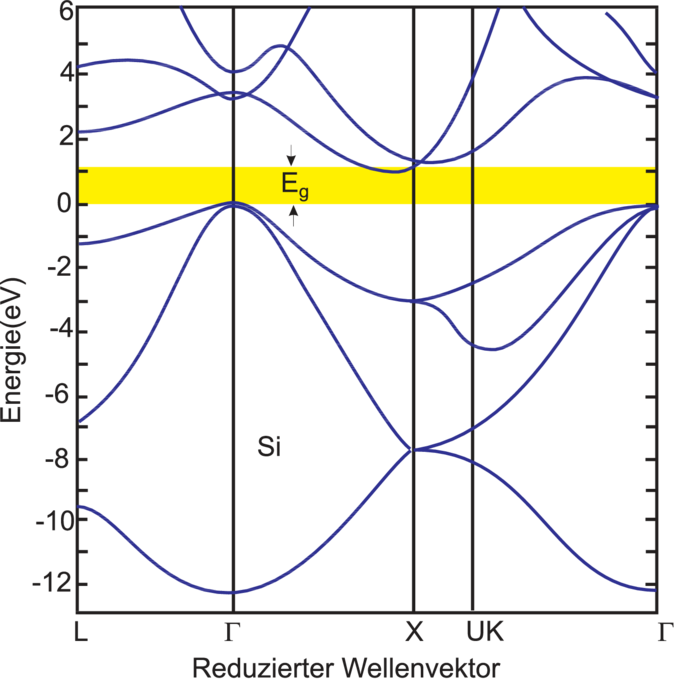
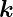
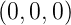 ), aber das Minimum der Leitungsband–Unterkante
liegt bei
), aber das Minimum der Leitungsband–Unterkante
liegt bei 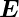 können nicht nur die Elektronen im Leitungsband (wie bei
den Metallen) Energie aufnehmen, sondern auch die im
Valenzband. Vereinfachend wird dies beschrieben durch die
Energieaufnahme der Löcher.
können nicht nur die Elektronen im Leitungsband (wie bei
den Metallen) Energie aufnehmen, sondern auch die im
Valenzband. Vereinfachend wird dies beschrieben durch die
Energieaufnahme der Löcher.
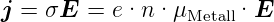
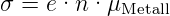
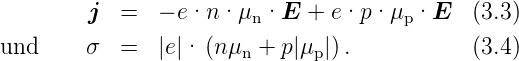
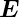 zuzulassen. Dann gilt für die betrachteten
Bänder die sog.
zuzulassen. Dann gilt für die betrachteten
Bänder die sog. 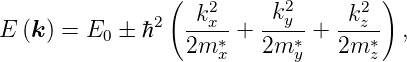
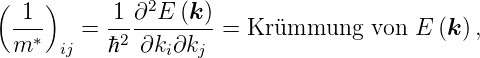
![∫∞
n = D (E )f(E, T )dE (3.7)
L
EL
∫EV
und p = DV (E )[1 − f(E, T)]dE, (3.8)
− ∞](phys_elektr603x.png)
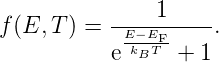
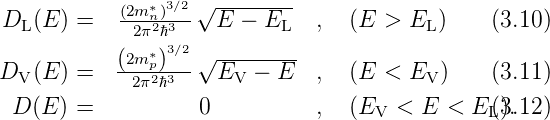
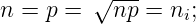
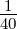
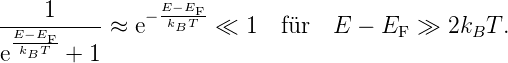
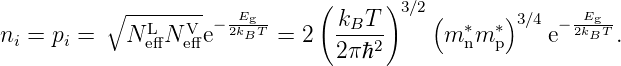
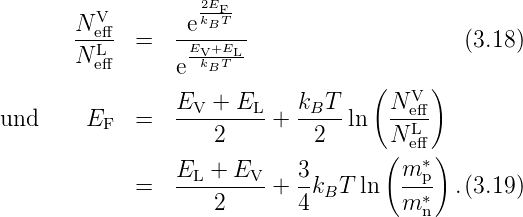
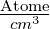 .
.


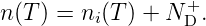
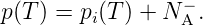
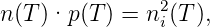
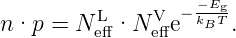
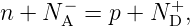
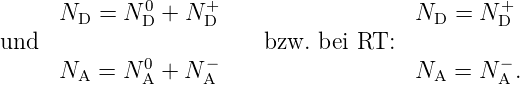
![0 [ EDk−ETF]
ND = ND · 1 + e B (3.26)
[ EF−EA]
und analog NA = NA0· 1 + e kBT . (3.27)](phys_elektr619x.png)
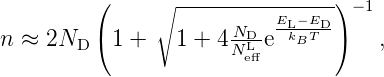
 abhängen können; die folgenden Aussagen gelten für relativ
kleine Feldstärken.
abhängen können; die folgenden Aussagen gelten für relativ
kleine Feldstärken.
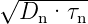 bzw.
bzw. 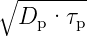 )
sind, verändert die Rekombination entlang des Wegs die
Stromdiche der Elektronen oder Löcher. Die entsprechenden
Diffusionslängen in
)
sind, verändert die Rekombination entlang des Wegs die
Stromdiche der Elektronen oder Löcher. Die entsprechenden
Diffusionslängen in 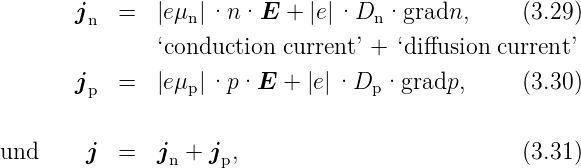
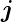
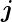
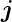
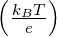
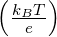
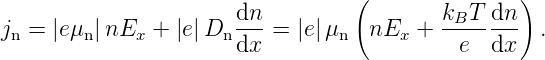
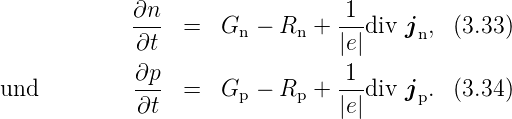
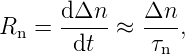
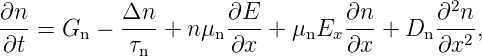
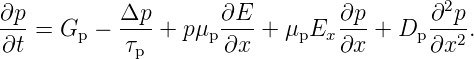
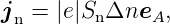
 Lizenzinformationen
Lizenzinformationen