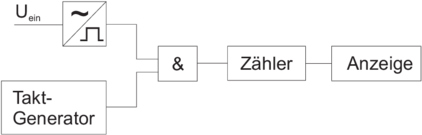
| Abbildung 4.88.: | Messung von Zeit oder Periodendauer. |

Frequenz und Zeitmessungen werden auf die Bestimmung einer Periodendauer, beziehungsweise auf die Zählung von Pulsen eines stabilen Generators zurückgeführt. Zeit und damit auch Frequenz ist die am genauesten bestimmbare physikalische Grössen.
Abbildung 4.88 zeigt die Messung einer Zeit oder einer Periodendauer. Die Eingangsspannung wird in eine Rechteckspannung übergeführt (durch eine Triggerstufe). Diese Rechteckspannung steuert das Tor (AND-Gatter), das die Taktimpulse eines stabilen Oszillators auf einen Zähler und damit auf eine Anzeige schaltet.
Die Periodendauermessung ist umso genauer, je länger die Periodendauer istAchtung!.
Wenn die Taktfrequenz f0 ist und die Periodendauer τ, dann gilt für die Auflösung 𝜀
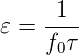 | (4.1) |
Typischerweise ist f0 1 MHz oder 10 MHz.
Gleichung (4.1) kann für Frequenzen fm so umgeschrieben werden:
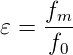 | (4.2) |
Die Auflösung der Periodendauermessung ist in der Tabelle 4.4 zusammengefasst.
| τ | fm | 10Hz | 100Hz | 1kHz | 10kHz | 100kHz | 1MHz | 10MHz |
| 10μs | 100kHz | - | - | - | - | 1 | 0.1 | 0.01 |
| 100μs | 10kHz | - | - | - | 1 | 0.1 | 0.01 | 10−3 |
| 1ms | 1kHz | - | - | 1 | 0.1 | 0.01 | 10−3 | 10−4 |
| 10ms | 100Hz | - | 1 | 0.1 | 0.01 | 10−3 | 10−4 | 10−5 |
| 100ms | 10Hz | 1 | 0.1 | 0.01 | 10−3 | 10−4 | 10−5 | 10−6 |
| 1s | 1Hz | 0.1 | 0.01 | 10−3 | 10−4 | 10−5 | 10−6 | 10−7 |
Kehrt man das Messprinzip aus Abb. 4.88 um, so erhält man den Frequenzmesser nach Abb. 4.92. Hier wirkt der Taktgenarator als Schalter für den Impulsstrom, der aus der Eingangsspannung durch einen Rechteckformer abgeleitet wurde. Die restliche Schaltung mit der Anzeige bleibt gleich.
bei einer Torzeit T ist die Auflösung 𝜀 der Messung der Frequenz fm durch
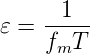 | (4.3) |
gegeben. Für die Auflösung der Frequenzmessung gilt Tabelle 4.4, aber mit vertauschten Benennungen. Horizontal ist nun die zu messende Frequenz, Vertikal die Torzeit des Messgerätes. Eine Implementation dieser Schaltung findet man in Abb. 4.93 und Abb. 4.94.
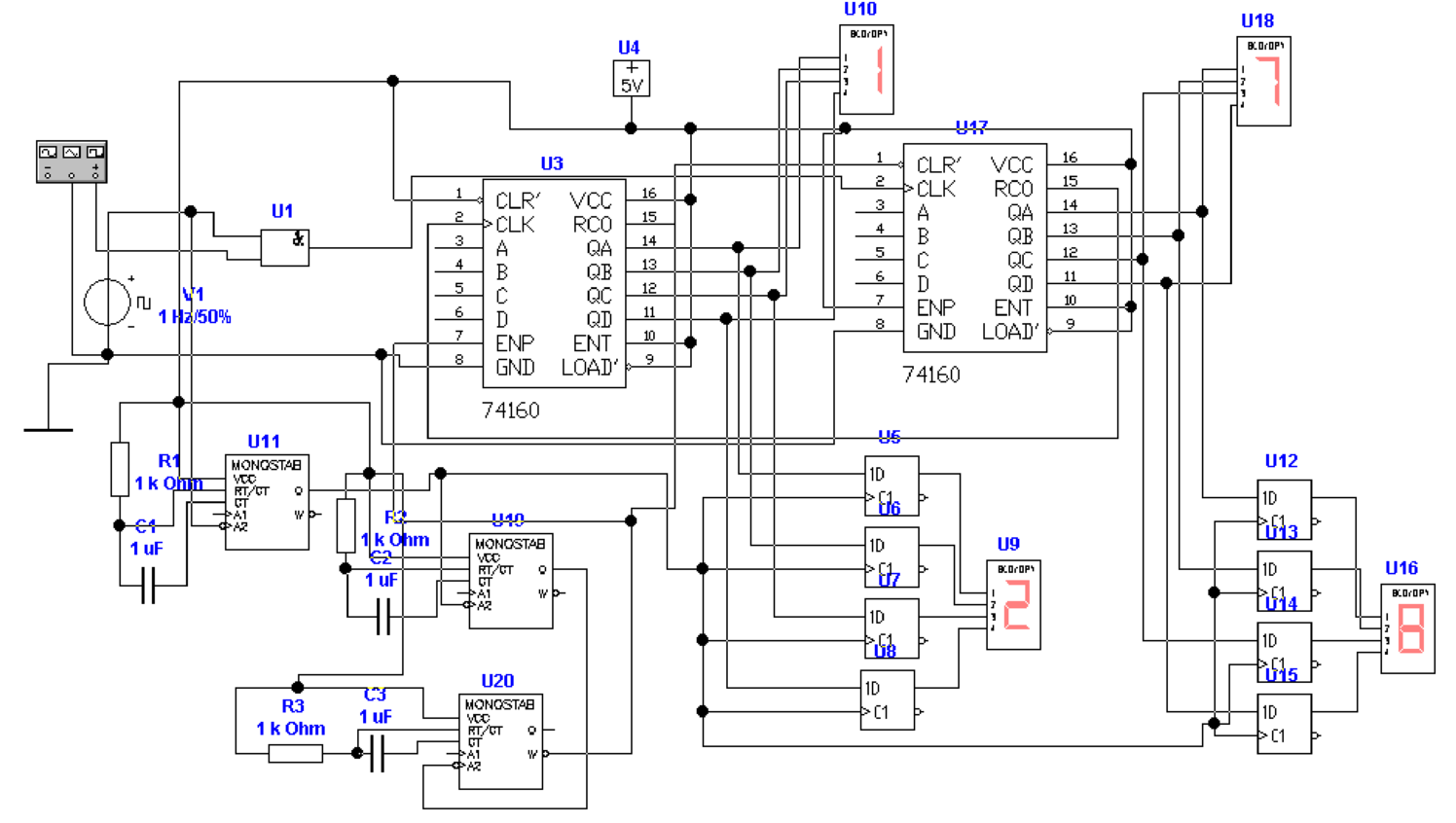
| Abbildung 4.94.: | Schaltung für eine Frequenzmessung. Der Unterschied zur Periodendauermessung liegt alleine in der Taktfrequenz des Referenzoszillators V1! |
Aus der Tabelle 4.4 kann man ableiten, dass bei vorgegebener Messdauer hohe und tiefe Frequenzen sehr genau gemessen werden können, mittlere Frequenzen jedoch nicht. Wenn T die Messdauer und f0 die Taktfrequenz des Messoszillators ist, gilt für die Genauigkeit
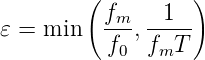 | (4.4) |
Aus Gleichung (4.4) wird Tabelle 4.5 berechnet.
| T | 1 Hz | 10 Hz | 100 Hz | 1 kHz | 10 kHz | 100 kHz | 1 MHz |
| 10 s | 10−6 | 10−5 | 10−4 | 10−4 | 10−5 | 10−6 | 10−7 |
| 1 s | 10−6 | 10−5 | 10−4 | 10−3 | 10−4 | 10−5 | 10−6 |
| 0.1 s | - | 10−5 | 10−4 | 10−3 | 10−3 | 10−4 | 10−5 |
| 0.01 s | - | - | 10−4 | 10−3 | 10−2 | 10−3 | 10−4 |
| 1 ms | - | - | - | 10−3 | 10−2 | 10−2 | 10−3 |
| Tabelle 4.5.: | Genauigkeit der Frequenzmessung für eine Messdauer T bei einer Taktfrequenz von 1 MHz. |
Das Verhältniszählverfahren nach Abb. 4.95 umgeht dieses Problem. Das Signal des Taktgenerators f0 wird nach einem Teiler durch m auf den Daten- (D-) Eingang eines Flip-Flops gegeben. Die zu messende Frequenz f wird über einen Rechteckformer an den Clockeingang des D-Flip-Flops gegeben. Wenn der Ausgang des Teilers von 0 auf 1 wechselt, wird dieser Zustand bei der nächsten steigenden Flanke des Eingangssignals auf den Ausgang übertragen. Damit werden über die zwei AND-Gatter die Zähler freigegeben. Der untere Zähler zählt nun die Pulse des Taktoszillators n. Der obere Zähler zählt die Pulse des Eingangssignals k. Wenn das Eingangssignal sehr schnell ist, zählt der obere Zähler im wesentlichen den Teilerfaktor ñ des Teilers. Bei langsamen Eingangssignalen können noch zusätzliche Werte dazukommen. Die gesuchte Eingangsfrequenz f ist
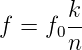 | (4.5) |
| f | k | n | fgemessen |
| 5.6789123 Hz | 6 | 1056540 | 5.6789141 ± 0.000006Hz |
| 3456.1234 Hz | 3457 | 1000253 | 3456, 1256 ± 0.004Hz |
| 876985.134 Hz | 876986 | 1000000 | 876986 ± 0.9Hz |
| Tabelle 4.6.: | Beispiele für die Verhältnismessung mit einer Torzeit von 1 s und einer Taktfrequenz von f0 = 1MHz |
Tabelle 4.95 zeigt für drei exemplarische Freqenzen die
Funktionsweise des Zählers. Der Zähler, k, ist immer die
Eingangsfrequenz f aufgerundet auf die nächste ganze Zahl
k = sup f. Der Nenner ist dann n = inf 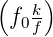 . Also ist
letztlich
. Also ist
letztlich
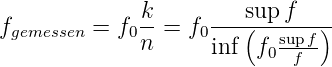 | (4.6) |
Als frequenzbestimmendes Glied in Zählern verwendet man häufig Quarze. Das Ersatzschaltbild eines Quarzes (Abb. 4.96) besteht aus der kapazität C und der Induktivität L. Die beiden Impedanzen bilden einen Serienschwingkreis, der die mechanische Resonanz nachbildet. R ist der Dämpfungswiderstand und C0 die Kapazität der Zuleitungen. Die obigen Werte können aus den Werten der mechanischen Resonanz abgeleitet werden[Kne78]. Tietze-Schenk[TS80] geben als typische Werte für einen 4MHz-Quarz an, dass L = 100mH, R = 100Ω, C = 0.015pF, Q = 25000 und C0 = 5pF. Bei Schwingkreisen ist die Dämpfung immer dann besonders klein, wenn L gross und C klein ist.
Jeder Quarz hat zwei Resonanzen, die Serienresonanz sowie die Parallelresonanz, in der auch die Anschlusskapazitäten eingehen. Die Impedanz des Schwingquarzes ist
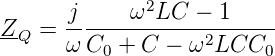 | (4.7) |
Es gibt also zwei Extremalwerte: einmal wird ZQ = 0 und einmal ZQ = ∞. Die erste Resonanz heisst Serienresonanz. Für sie gilt, sofern man R vernachlässigt,
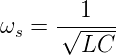 | (4.8) |
Im Gegensatz dazu ist die Parallelresonanz (Nullstelle im Nenner)
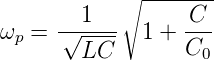 | (4.9) |
Aus Gleichung (4.9) ist ersichtlich, dass die Parallelresonanz höher liegt. Beim oben erwähnten 4 MHz-Quarz ist dies 0,15 %. Die Serienresonanz hängt, anders als die Parallelresonanz, nicht von den Anschlusskapazitäten ab. Sie ist also in jedem Falle stabiler.
Abb. 4.97 zeigt, dass man mit einem Kondensator in Serie Die Resonanzfrequenz einstellen kann. Die modifizierte Impedanz des Quarzes ist
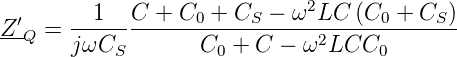 | (4.10) |
Mit der Einstellbarkeit der Serienresonanzfrequenz hängt sie nun auch von C0, der Streukapazität, ab. Allerdings ist schnell ersichtlich, dass für CS →∞ Gleichung (4.10) in Gleichung (4.9) übergeht. Die Parallelresonanzfrequenz wird übrigens bei der Abstimmung nicht verändert. Für die einstellbare Serienresonanzfrequenz bekommt man
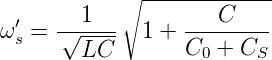 | (4.11) |
Da bei allen Quarzen C «C0 + CS ist bekommt man
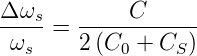 | (4.12) |
Wenn die Kapazität CS → 0 geht, ist die serienresonanzfrequenz gleich der Parallelresonanzfrequenz, mit all den Stabilitätsproblemen. Es ist also sinnvoll, dass man CS möglichst gross lässt.
Als Taktgeneratoren für die Frequenz- bzw. Periodendauermessgeräte kommen Quarz-Oszillatoren in Frage. Abb. 4.98 zeigt einen solchen Oszillator nach Colpitts. Wichtig bei diesem Oszillator, wie auch beim Hartley-Oszillator in der Abb. 4.99 ist, dass die Impedanzen klein gegen den Dämpfungswiderstand R des Quarzes sind.
Der Colpitts- und der Hartley-Oszillator unterscheiden sich durch die Art der Spannungsrückkopplung, Bei Colpitts wird die Kapazität geteilt, während bei Hartley Die Spule angezapft wird. Dieses ist sehr viel teurer als zwei Kondensatoren, ausser bei sehr hohen Frequenzen„ bei denen man die Leitungsinduktivitäten auf der Printplatte ausnutzt.
Abb. 4.100 zeigt die heute übliche Bauart von Quarzoszillatoren mit Invertern als Verstärkern. Das Ausgangssignal des Inverters wird über ein RC-Glied und den Quarz an den Eingang zurückgekoppelt. Der einstellbare Kondensator dient, wie schon bei den vorherigen Aufbauten dazu, die Frequenz im Promille-Bereich abzustimmen.
Wenn Schaltungen aufgebaut werden müssen, kann man spezielle Treiberschaltungen für Quarze verwenden. Teilweise sind die Treiberschaltungen auch in den Bausteinen für Zähler usw. eingebaut.
Wenn Frequenzen schnell gemessen werden sollen, oder wenn ein Oszillator mit einem bestimmten Teilerverhältnis an einen Referenzoszillator gekoppelt werden soll, verwendet man Phasenregelkreise, englisch Phase Locked Loop oder PLL. Abb. 4.101 zeigt das Prinzipbild, wenn die Ausgangsfrequenz des spannungsgesteuerten Oszillators gleich der Referenzfrequenz sein soll. Die Frequenz fs des spannungsgesteuerten Oszillators ist
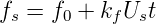 | (4.13) |
Am Phasendetektor entsteht eine Ausgangsspannung, die, zumindestens in der Nähe des Nullpunktes (bei dem beide Frequenzen gleich wären) linear ist.
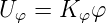 | (4.14) |
Wenn die Referenzfrequenz fref und die Frequenz fs unterschiedlich sind, nimmt die Phasenverschiebung φ mit der Zeit zu: die Strecke hat ein integrierendes Verhalten. Im eingeschwungenen Zustand sind die Frequenzen exakt gleich, die verbleibende Phasenverschiebung ist:
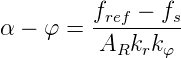 | (4.15) |
wobei AR die Schleifenverstärkung ist. α ist eine gewollt eingeführte, konstante Phasenverschiebung. Der Frequenzgang dieser Regelschleife kann wie folgt berechnet werden:
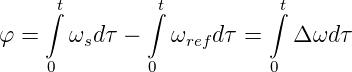 | (4.16) |
Nun wird die Frequenz fs sinusförmig mit ωm moduliert.
Mit Δω(t) =  cos ωmt bekommt man für die Phase
cos ωmt bekommt man für die Phase
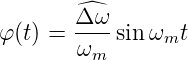 | (4.17) |
In komplexer Schreibweise wird Gleichung (4.17)
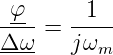 | (4.18) |
Dies ist der Frequenzgang eines Integrators. Schliesslich ist die komplexe Schleifenverstärkung
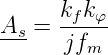 | (4.19) |
Gleichung (4.19) suggeriert, dass das Integratorverhalten der Strecke die Regelung sehr einfach macht. Nun sind aber alle realen Phasendetektoren mit mehr oder weniger langen Verzögerungszeiten behaftet. Wie im Abschnitt 2.4.3 gezeigt, folgt daraus, dass im Regelkreis die Phasenverschiebung (nicht die zwischen den Frequenzen fref und fs!) proportional zur Frequenz ist. Damit wird es sehr schwierig, den Regelkreis zu stabilisieren. Die Dimensionierung von Phasenregelkreisen gehört somit nicht zu den einfachsten Aufgaben.
In Abb. 4.102 wird gezeigt, wie mit zwei zusätzlichen
Teilern beliebige Frequenzverhältnisse gelockt werden können.
Der Phasenregelkreis erzwingt, dass 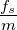 =
= 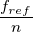 ist. Damit
erhält man für die Frequenz des spannungsgesteuerten
Oszillators
ist. Damit
erhält man für die Frequenz des spannungsgesteuerten
Oszillators
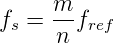 | (4.20) |
Bei PLL-UKW-Empfängern könnte zum Beispiel fref = 4MHz sein Das Frequenzraster ist 50 kHz, also muss n = 4000∕50 = 80 sein. Wenn m einstellbar ist mit m = 1940…2160 kann der gesamte UKW-Bereich eingestellt werden.
Abb. 4.103 zeigt, dass man ein Abtast-Halteglied oder Sample/Hold-Glied eine phasenempfindliche Detektion durchführen kann. Der spannungsgesteuerte Oszillator fosc triggert den Monoflop, der seinerseits einen Schalter betätigt, der die momentane Spannung der Referenz (Frequenz fref) auf einem Kondensator speichert. Abb. 4.104 zeigt auf der linken Seite die entsprechenden Spannungsverläufe.
Wenn die beiden Frequenzen gleich sind, und nur die Phase nicht übereinstimmt, dann misst so das Sample/Hold-Glied die zu dieser Phasenlage gehörige Spannung. Voraussetzung ist, dass das Eingangssignal sinusförmig oder dreiecksförmig ist. Die resultierende Kennlinie ist in Abb. 4.104 auf der rechten Seitze gezeigt. Dadurch, dass positive und negative Ausgangswerte für beide Polaritäten der Phase auftreten, hat dieser Detektor einen sehr eingeschränkten Fangbereich.
Besser in dieser Beziehung ist der Phasendetektor nach Abb. 4.105. Die beiden Eingangsfrequenzen f1 und f2 werden auf den Setz- (S-)Eingang jeweils eines RS-Flip-Flops gegeben. HinweisVoraussetzung, dass diese Schaltung funktioniert ist, dass die Wellenform der beiden Eingangsfrequenzen jeweils kurze Pulse sind. Wenn zum Beispiel f1 in der Phase früher ist als f2 dann wird das obere SR-Flip-Flop gesetzt. Sein Ausgangssignal geht nach 1. Da das untere RS-Flip-Flop noch nicht gesetzt ist, ist das Ausgangssignal des AND-Gatters 0. Wenn nun der Puls der unteren Frequenz f2 auch das untere Flip-Flop am Ausgang auf 1 setzt, dann setzt das AND-Gatter die beiden Flip-Flops zurück. Wenn die untere Frequenz in der Phase vorgeht, dann gibt entsprechend das untere Flipflop Pulse ab. Der Summierer gewichtet das obere Flip-Flop mit + und das untere mit -. Schliesslich werden die Pulse mit einem Tiefpassfilter geglättet.
Abb. 4.106 zeigt die Kennlinie dieses Detektors. Solange die Phase von f1 voreilt, ist das Ausgangssignal positiv, solange sie nacheilt, negativ. Damit verhält sich diese Schaltung wesentlich gutmütiger als das Sample/Hold-Glied.
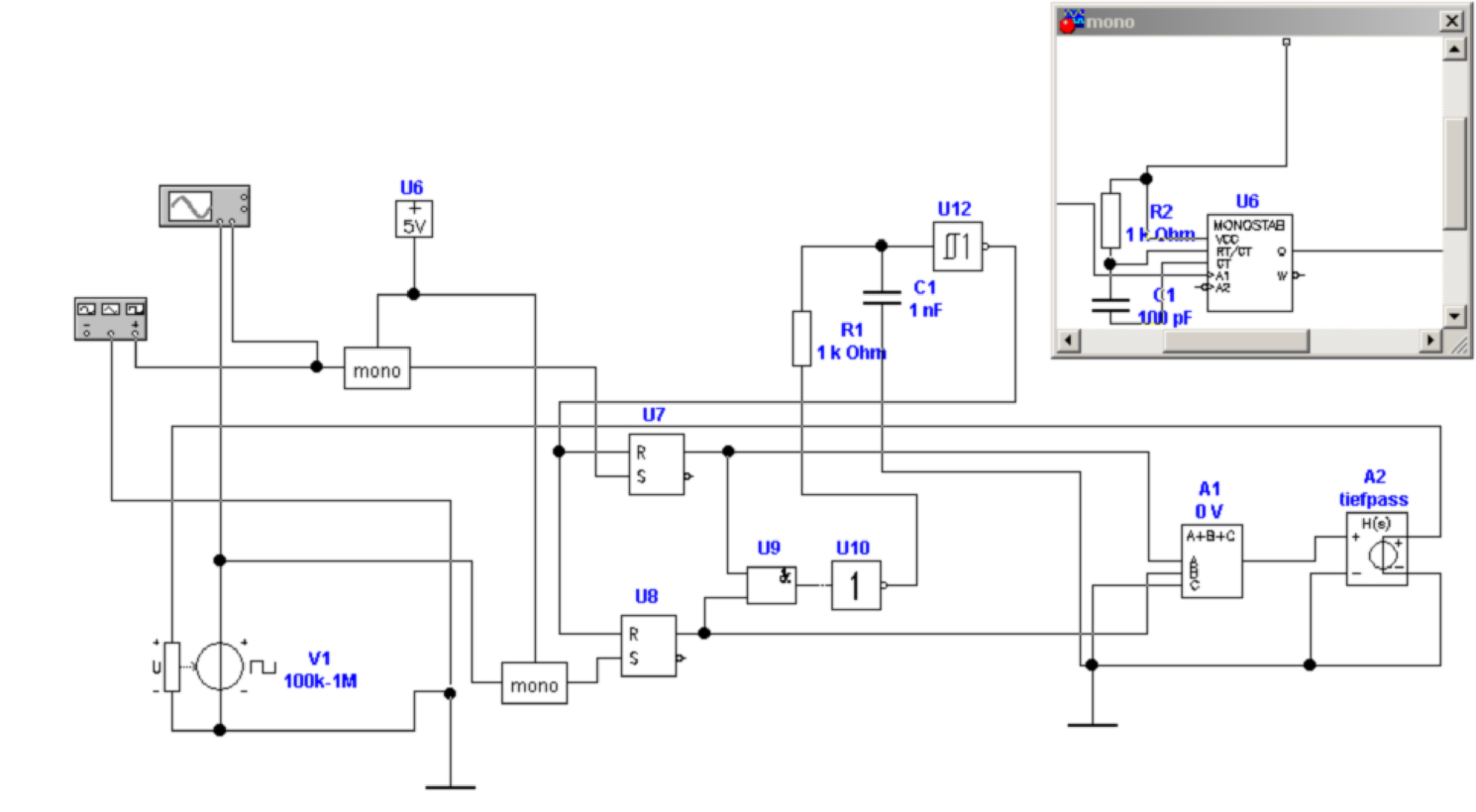
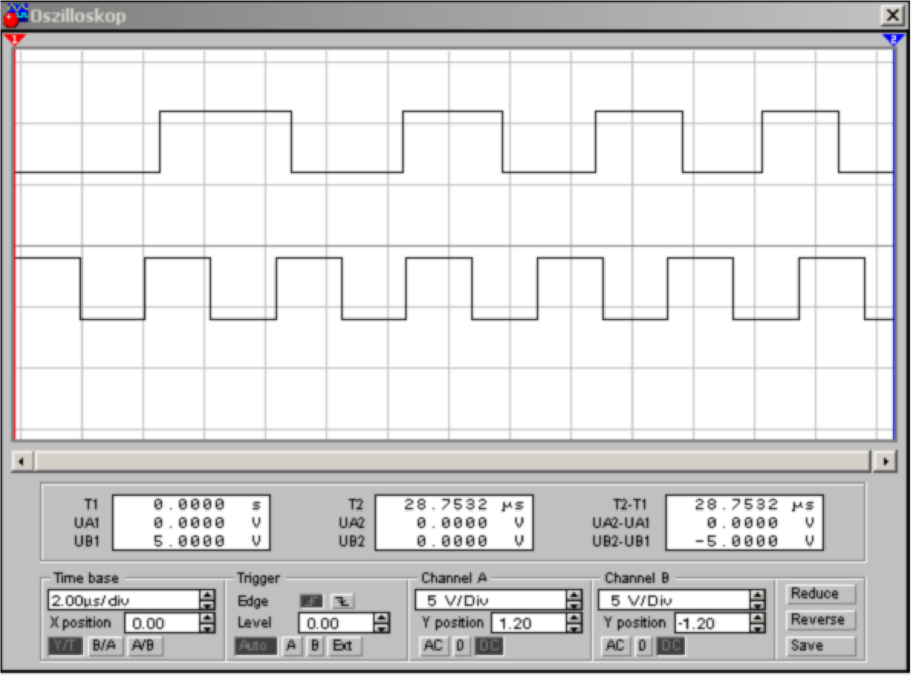
| Abbildung 4.107.: | Implementierung eines vorzeichenrichtigen Phasendetektor. Unten ist gezeigt, wie der gesteuerte Oszillator sich der Frequenz nähert. |
Abb. 4.107 zeigt schliesslich, wie so ein Phasendetektor aufgebaut wurde. Eine spannungsgesteuerte Rechteckquelle V 1 ist der Nachlaufoszillator, der Referenzoszillator wird durch den Funktionsgenerator realisiert. Die beiden Signale werden durch jeweils einen Monoflop, dessen internes Schaltbild man im Einschub oben rechts sehen kann, zu kurzen Pulsen geformt. Die RS-Flip-Flops U7 und U8 detektieren die Phase, zusammen mit dem AND-Gatter U9. Anders als in der Literatur angegebn[TS80] muss man im Simulationsprogramm[Des00]eine Verzögerungsstreckt bestehend aus den beiden Invertern/Schmitt-Triggern U10 und U12 anwenden. Die Ausgangssignale von U7 und U8 werden in A1 subtrahiert und in A2 tiefpassgefiltert. Dieses Signal steuert den spannungsgesteuerten Rechteckoszillator.
Unten in Abb. 4.107 sind die beiden Kurvenformen der Oszillatoren zu sehen. es wird deutlich, dass die Phasenregelschlaufe das obere Signal an das untere Referenzsignal heranführt.
Wenn Zeiten im Bereich von μs bis 100 ps elektrisch
gemessen werden sollen, dann wird häufig das Verfahren nach
Abb. 4.108 verwendet. Dabei wird, nach einem Startpuls
eine Rampe hochgefahren. Der Stoppuls triggert einen
Sample/Hold, der zu diesem zeit die Amplitude misst. Aus
der Anstigsrate α = 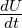 und der gemessenen Spannung Ut
errechnet man die Zeit
und der gemessenen Spannung Ut
errechnet man die Zeit
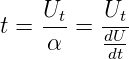 | (4.21) |
Die Zeitmessung nach Abb. 4.108 funktioniert deshalb so gut, da es möglich ist, Sample/Hold-Verstärker zu bauen, deren Einschaltzeitpunkt auf wenige ps genau ist, auch wenn der ganze Schaltvorgang mehrere hundert ps dauern sollt. Diese lange Zeitdauer gibt einen systematischen, also korrigierbaren Fehler.
Die Messung von magnetischen Feldern kann über induzierte Spannungen
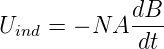 | (4.22) |
erfolgen. Hier ist N die Windungszahl, A die Querschnittsfläche und B die magnetische Induktion. Eine einfache und für viele Zwecke ausreichende Möglichkeit sind rotierende Spulen. Die magnetische Induktion in Gleichung (4.22) wird dabei durch die Änderung der effektiven Fläche A erreicht.
Bei nichtlinearen magnetischen Materialien, wie in Abb.
4.109, rechts, gezeigt kann mit einem Transformator das
externe Feld gemessen werden. Abb. 4.109, links, zeigt einen
nichtlinearen Transformator. Die Nichtlinearität sei durch die
Gleichung B(H) = μ0![[H + K ·H3 ]](phys_elektr860x.png) modelliert. Moduliert
man H mit der oberen Spule in Abb. 4.109 mit der Frequenz
ω und existiert ein externes Feld Hext dann ist das effektive
Feld H(t) = Hext + H0 sin(ωt). Die magnetische Induktion
wird dann
modelliert. Moduliert
man H mit der oberen Spule in Abb. 4.109 mit der Frequenz
ω und existiert ein externes Feld Hext dann ist das effektive
Feld H(t) = Hext + H0 sin(ωt). Die magnetische Induktion
wird dann
Ausmultipliziert und nach Anwendung der Rechenregeln für trigonometrische Funktionen ergibt sich
Gleichung (4.24) zeigt, dass die Frequenzkomponente bei 2ω nur auftritt, wenn Hext ⇔ 0 ist. Die Grösse des externen magnetischen Feldes Hext kann dann mit
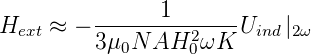 | (4.25) |
angegeben werden. Da die Amplitude des modulierten Feldes quadratisch im Nenner erscheint, kann (in Grenzen) die Empfindlichkeit durch Erhöhung der Modulationsamplitude gesteigert werden.
Wenn in einem Magnetfeld senkrecht zur Magnetfeldrichtung ein Strom fliesst, dann bewirkt die Lorentzkraft, dass die zur Magnetfeldrichtung und zur Stromrichtung senkrechten Seiten des Leiters geladen werden. Dieser Effekt heisst Hall-Effekt. Zwischen den Elektroden in y-Richtung in Abb. 4.110 tritt dann die Hallspannung
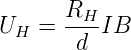 | (4.26) |
auf. Dabei ist angenommen worden, dass die Länge sehr viel grösser als Breite sei. Damit kann man eine Betrachtung des stationären Zustandes durchführen.
Die Lorentzkraft auf ein bewegtes Ladungsteilchen ist
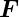 L = q(
L = q(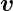 ×
×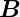 . Im Gleichgewicht wird sie durch die
elektrostatische Kraft des Hall-Feldes
. Im Gleichgewicht wird sie durch die
elektrostatische Kraft des Hall-Feldes
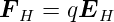 | (4.27) |
kompensiert. Aus der Betrachtung des Kräftegleichgewichts folgt
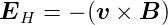 | (4.28) |
Gleichung (4.28 ist allgemeingültig. Für die folgende
Betrachtung nehmen wir an, dass Magnetfeld und
Stromflussrichtung orthogonal seien. Dann ist die induzierte
Hallspannung UH = −bvxB. Aus der mittleren Geschwindigkeit
vx der Ladungsträger kann, bei bekannter Ladungsträgerdichte
n, die Stromdichte jx,n = nqvx = 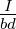 berechnet werden. Diese
Stromdichte ist die Folge des Stromes I, der über die
Stirnfläche b·d eingekoppelt wird. Man hat also jx =
berechnet werden. Diese
Stromdichte ist die Folge des Stromes I, der über die
Stirnfläche b·d eingekoppelt wird. Man hat also jx = 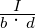 und damit für negative Ladungsträger (Betrag der Ladung:
q)
und damit für negative Ladungsträger (Betrag der Ladung:
q)
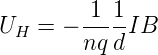 | (4.29) |
Die Abhängigkeit von der Ladungsträgerdichte (n für negative Ladungen und p für positive Ladungen) und von der Ladung wir in einer Hall-Konstante RH zusammengefasst. Für die beiden Ladungsträgerpopulationen ergeben sich
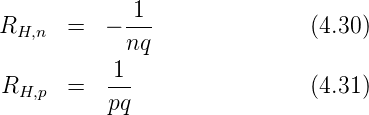
Die funktionale Abhängigkeit ist in Abb. 4.110 gezeigt.
In einem Widerstand mit konstantem Querschnitt und homogener Materialzusammensetzung sind die Äquipotentialflächen der Spannung senkrecht zur Stromrichtung. Liegt eine Hallspannung vor, addiert sich deren elektrisches Feld zum ursprünglichen elektrischen Feld. Die Äquipotentialflächen werden, wie in Abb. 4.111 gezeigt, um den Hall-Winkel Θh gekippt.
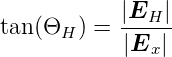 | (4.32) |
Unter Verwendung der Hallbeweglichkeit μH der Ladungsträger, die sich nicht sehr von der Driftbeweglichkeit μdrift unterscheidet, ist der Hall-Winkel
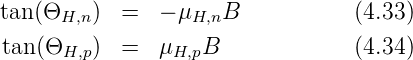
Feldplatten, wie sie in Abb. 4.112 gezeigt werden, verwenden den gleichen physikalischen Mechanismus wie die Hall-Sonden, aber in longitudinaler Weise. In einem Leiter, wie er in der Abbildung rechts gezeigt ist, ist der Widerstand ohne Magnetfeld
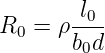
wenn l0 wie üblich die Länge des Leiterstückes ist, b0 die Breite und d die Dicke.
Wenn andere Effekte des Magnetfeldes vernachlässigt werden, tritt immer noch die Verkippung der Äquipotentialflächen des elektrischen Feldes auf. Wenn die Probe breiter als lang ist, kann man davon ausgehen, dass das Magnetfeld die Wege um
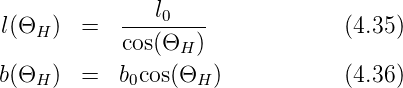
verlängert. Wie beim Halleffekt ausgeführt, ist die Verlängerung eine Funktion des Hall-Winkels ΘH. Durch den längeren Weg erhöht sich der Widerstand um
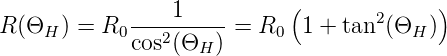 | (4.37) |
Wenn man die beim Halleffekt definierte Hall-Beweglichkeit verwendet, wird der Widerstand
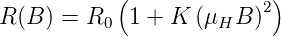 | (4.38) |
Um die Forderungen nach einem kurzen Leiterstück und nach langen Wirkungswegen zu erfüllen, werden, wie in Abb. 4.112 gezeigt, mäanderierende Strukturen verwendet. Bei ihnen kann man für jedes Teilstück davon ausgehen, dass die in der gleichen Abbildung rechts gezeigte Situation vorliegt. Abb. 4.113 schliesslich zeigt die resultierende Kennlinie einer Feldplatte. Um eine hohe Empfindlichkeit zu erreichen, müssen Werkstoffe mit hoher Ladungsträgerbeweglichkeit verwendet werden. Deshalb werden, wie bei Hall-Generatoren InSb, InAs, Si und GaAs verwendet.
Unter dem Einfluss eines externen magnetischen Feldes verändern gewisse ferromagnetische Werkstoffe ihre Leitfähigkeit. Eine unabdingbare Voraussetzung für diesen Effekt ist die Existenz einer Anisotropie der elektrischen Leitfähigkeit.
Wenn man annimmt, dass ein Material die Leitfähigkeiten ρp parallel zur Magnetisierungsrichtung und ρs senkrecht dazu hat, kann eine einfache Ableitung nach[TO98] angegeben werden.
Wir nehmen an, dass die Magnetisierung zur Stromrichtung den Winkel Θ einschliesst. Dann ergeben sich für die Felder (siehe auch 4.115)
und die Ströme
Aus den Materialeigenschaften ergeben sich die Beziehungen
Die Gleichung für das elektrische Feld Gleichung (4.39) wird mit Gleichung (4.41) kombiniert
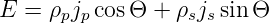
Wir berechnen js aus Gleichung (4.40)
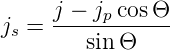
Durch Einsetzen erhalten wir
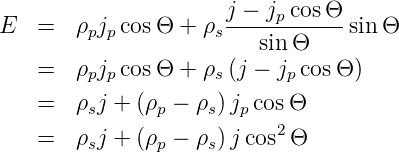
Auf andere Weise geschrieben ist das Resultat
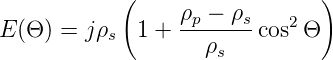 | (4.42) |
Diese Gleichung kann auf den Widerstand umgerechnet werden.
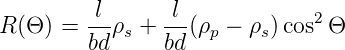 | (4.43) |
Die Vorzugsrichtung des Detektors wird über die Achse der Magnetisierung eingestellt. Abb. 4.114 rechts zeigt Hysteresekurven entlang der magnetisch harten (rechts) und magnetisch leichten Achse (links).
Entlang der magnetisch harten Achse gilt für kleine Feldstärken Hy < Hk
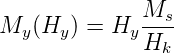 | (4.44) |
Wenn die äussere magnetische Feldstärke nur eine Komponente in die y-Richtung aufweist, und die magnetisch harte Achse dieses Materials auch in diese Richtung zeigt, so bekommt man aus Abb. 4.116 unter Vernachlässigung von Randeffekten (Entmagnetisierung) für den Winkel Θ und die Magnetisierungen, bzw. die Feldstärken
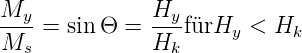 | (4.45) |
Umgeformt erhält man für kleine Feldstärken Hy
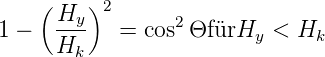 | (4.46) |
Ausserhalb dieses Bereiches ergibt sich der gewöhnliche Widerstand. Zusammenfassend erhält man

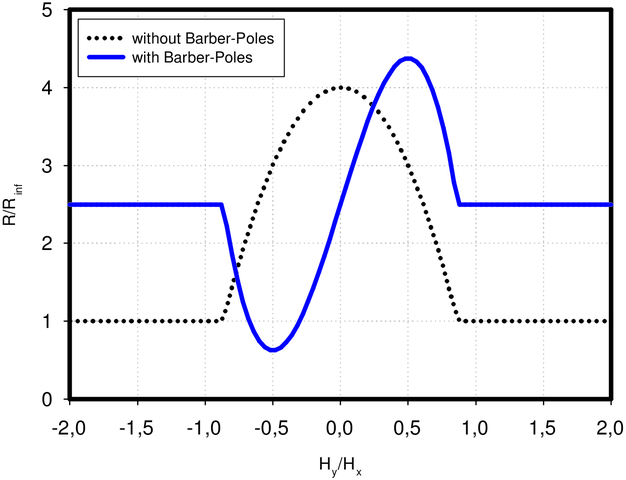
| Abbildung 4.117.: | Aufbau eines magnetoresistiven Sensors mit ’Barber Poles’. Rechts die Kennlinie mit (durchgezogen) und ohne ’Barber Poles’ (gestrichelt) |
Abb. 4.117 zeigt rechts die Kennlinie des Sensors. Die quadratische Abhängigkeit ist sehr schön zu sehen. Bei der Anwendung in Messgeräten stört diese quadratische Abhängigkeit jedoch. Deshalb versucht man, die Stromrichtung und die Magnetisierung M im 450-Winkel festzulegen. Mit Metallstreifen in der gewünschten Richtung, wie in der Abb. 4.117, links, gezeigt, kann dies erreicht werden. Mit diesen sogenannten ’Barber Poles’ ist die Linearisierung möglich. Die dazugehörige Kennlinie wird auf der rechten Seite gezeigt.
Mit dem Josephson-Effekt ist es möglich, sehr kleine
Magnetfelder zu messen. Beim Gleichstrom-Josephson-Effekt
fliessen Elektronen paarweise (Cooper-Paare) durch die
Oxidschicht in Abb. 4.118, die als Tunnelübergang wirkt.
Wenn eine kritische Stromstärke IK überschritten ist, tritt
eine Potentialdifferenz auf. Sie rührt vom Tunneln einzelner
Elektronen her. Die kritische Stromstärke Ik ist abhängig
von der magnetischen Flussdichte 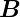 in der Ebene des
Tunnelüberganges.
in der Ebene des
Tunnelüberganges.
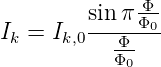 | (4.48) |
Dabei ist Φ magnetischer Fluss im Tunnelübergang. Das
elementare Flussquant ist Φ0 = 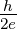 = 2.07 × 10−15Vs. I
k,0 ist
der supraleitende Strom ohne
= 2.07 × 10−15Vs. I
k,0 ist
der supraleitende Strom ohne 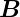 .
.
Bei einem SQUID (Superconducting Quantum Interference Device) nach Abb. 4.119 beeinflusst der Fluss durch die Öffnung des Ringes die Einteilchen-Wellenzustände der supraleitenden Elektronen. Der Fluss Φ bewirkt bei einem geeigneten Gleichstrom I eine periodische Abhängigkeit der Potentialdifferenz UDC an den Tunnelkontakten. Die Periode hängt vom magnetischen Flussquant Φ0 ab und ist, ausgedrückt im externen magnetischen Fluss B
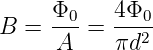 | (4.49) |
wobei d der Durchmesser des Ringes ist. Für einen Durchmesser von 1 mm erhält man für die Periode in B den wert 2,6 nT, was etwa 19000 mal weniger als das Erdmagnetfeld ist. Vergrössert man den Durchmesser des Ringes, steigt die Empfindlichkeit. Die Empfindlichkeit des SQUID beruht darauf, dass die grössere Fläche mehr Fluss umfängt. Mit geeigneten techniken lassen sich mit einem SQUID auch Bruchteile eines Flussquantes detektieren.
Wenn das SQUID nicht direkt an der Messstelle sitzen kann, z.B. wegen der notwendigen Kühlung, kann das Magnetfeld mit einer Spule detektiert und über Drähte und eine zweite Spule zum SQUID gebracht werden.
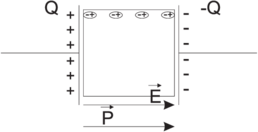
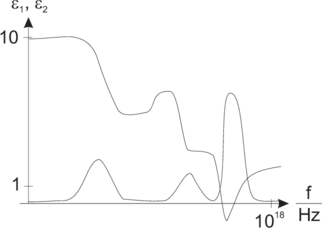
| Abbildung 4.120.: | Dielektrische Funktion. Links: Prinzipielle Messanordnung. Rechts typisches dielektrisches Spektrum |
In Medien hängt die Polarisation 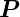 vom elektrischen Feld
vom elektrischen Feld
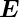 ab. Im Allgemeinen gibt es eine nichtlineare Abhängigkeit,
die tensoriellen Charakter hat. Für isotrope Materialien hat
man
ab. Im Allgemeinen gibt es eine nichtlineare Abhängigkeit,
die tensoriellen Charakter hat. Für isotrope Materialien hat
man 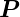 = χ𝜀0
= χ𝜀0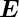 . Mit 𝜀r = 1 + χ erhält man für die elektrische
Flussdichte
. Mit 𝜀r = 1 + χ erhält man für die elektrische
Flussdichte
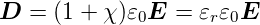 | (4.50) |
𝜀r ist im isotropen Falle die dielektrische Funktion. Sie
hängt vom Aufbau der Materie ab und reduziert das
elektrische Feld im Innern sowie die Kräfte auf Ladungen um
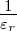 und erhöht die Kapazität von Kondensatoren um
𝜀r.
und erhöht die Kapazität von Kondensatoren um
𝜀r.
In nichtpolaren Medien ist die Verschiebungspolarisation
der einzige mögliche Mechanismus. Dabei werden die
Schwerpunkte der positiven und negativen Ladungswolken in
Atomen oder Molekülen gegeneinander verschoben. Bei polaren
Molekülen kann das äussere Feld die bestehenden Dipole und
Multipole ausrichten und so die Orientierungspolarisation
hervorrufen. Da thermische Fluktuationen die Orientierung in
einen zufälligen Zustand zu treiben versuchen, ist die
Orientierungspolarisation stark temperaturabhängig. Bei
zeitabhängigen äusseren Feldern wirkt sich weiter die
Trägheit der zu bewegenden Ladungen aus. Resonanzen und
ein frequenzabhängiger Response sind die Folge. Bei einem
äusseren Feld 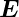 (ω) =
(ω) = 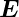 0 cos ωt muss Gleichung (4.50)
umgeschrieben werden.
0 cos ωt muss Gleichung (4.50)
umgeschrieben werden.
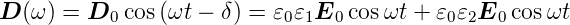 | (4.51) |
Amplitude und Phase sind D0 = 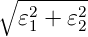 𝜀0E0 und
tan δ =
𝜀0E0 und
tan δ = 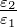 . Dies kann auch ausgedrückt werden, indem in
Gleichung (4.50) 𝜀r = 𝜀1 −j𝜀2 gesetzt wird und Flussdichte
und Feld frequenzabhängig angesehen werden.
. Dies kann auch ausgedrückt werden, indem in
Gleichung (4.50) 𝜀r = 𝜀1 −j𝜀2 gesetzt wird und Flussdichte
und Feld frequenzabhängig angesehen werden.
Nach Maxwell (Gleichung (A.2) erzeugt eine zeitlich sich
ändernde Flussdichte eine Stromdichte 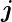 =
= 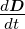 = jω𝜀0𝜀r
= jω𝜀0𝜀r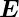 . 𝜀2
bestimmt also den Strom, der in Phase mit dem elektrischen
Feld ist. Dieser Strom verursacht durch Stösse mit den
Atomrümpfen, Defekten etc. Dissipation. 𝜀1 ist ein Mass für
die gespeicherte Ladung.
. 𝜀2
bestimmt also den Strom, der in Phase mit dem elektrischen
Feld ist. Dieser Strom verursacht durch Stösse mit den
Atomrümpfen, Defekten etc. Dissipation. 𝜀1 ist ein Mass für
die gespeicherte Ladung.
Ist das zu untersuchende Material leitfähig 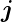 = σ
= σ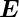 , dann
ist der Gesamtstrom
, dann
ist der Gesamtstrom
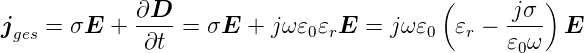 | (4.52) |
Man bezeichnet 𝜀r −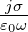 = 𝜀1 −j
= 𝜀1 −j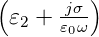 als
verallgemeinerte dielektrische Funktion. Die rechte Seite von
Abb. 4.120 zeigt ein typisches dielektrisches Spektrum.
als
verallgemeinerte dielektrische Funktion. Die rechte Seite von
Abb. 4.120 zeigt ein typisches dielektrisches Spektrum.
Die Leitfähigkeit für elektrischen Strom hängt von der Materialzusammensetzung, der Kristallinität und der Temperatur ab. Die Streuung von Ladungsträgern an Störstellen, Korngrenzen und die Anzahl der beweglichen Ladungsträger bestimmen die Leitfähigkeit.
In isotropen Metallen wirkt nach Anlegen einer Spannung an jedem Punkt eine Feldstärke, die die Elektronen beschleunigt. Streuung und Stösse bremsen die Elektronen wieder ab, so dass der Strom nicht über alle Grenzen wächst. Das elektrische Feld und der Strom hängen über die Leitfähigkeit σ (bei anisotropen Materialien ein Tensor) zusammen.
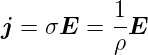 | (4.53) |
Der messbare Widerstand R bei einem Leiter der Länge l und mit dem Querschnitt A ist
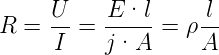 | (4.54) |
Nach dem Drude-Modell ist die Leitfähigkeit bei einem idealen Gitter gegeben durch
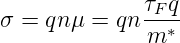 | (4.55) |
Mit wachsender Temperatur schwingen die Atomrümpfe stärker um ihre Ruhelagen. Dadurch behindern sie den Strom. Die mittlere freie Flugzeit τF nimmt ab. Letztlich nimmt der Widerstand zu.
Nach der Regel von Matthiessen ρ = ρG + ρP (T) erhält man den spezifischen Widerstand eines Metalls aus dessen Restwiderstand ρG, der die Wechselwirkung der Elektronen mit statischen Defekten beschreibt und aus einem temperaturabhängigen Teil.
Für viele nichtferromagnetische Metalle kann die Temperaturabhängigkeit des spezifischen Widerstandes aus der Debye-Temperatur ΘD berechnet werden.
![[ ]
ρ (T ) = ρ(T = Θ ) 1.17-T--− 0.17 fürT > 0.15Θ
p D ΘD D](phys_elektr920x.png) | (4.56) |
Bei sehr tiefen Temperaturen hängt der temperaturabhängige Teil des spezifischen Widerstandes wie T5 von der Temperatur ab: der spezifische Widerstand wird konstant beim spezifischen Restwiderstand des Materials.
Für sehr hohe Temperaturen kann Gleichung (4.55) linearisiert werden.
Dabei sind die Widerstandswerte bei den einzelnen Temperaturen mit Gleichung (4.56 berechnet worden. Wenn man T2 = ΘD setzt, ergibt sich
![( T )
---ρp(ΘD--)-0.83-−-1.17ΘD---- ----1----
αT1 = [ T-- ]· Θ − T fürT > 0.15ΘD
ρg + ρp(ΘD ) 1.17 ΘD − 0.17 D 1](phys_elektr922x.png) | (4.60) |
Bei Vernachlässigung des spezifischen Restwiderstandes ρg erhält man für hohe Temperaturen für den Temperaturkoeffizienten des Widerstandes
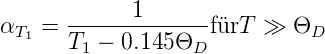 | (4.61) |
Aus den Debye-Temperaturen zwischen 50 K und 400 K ergeben sich bei 293 K Temperaturkoeffizienten zwischen 3.5 × 10−3…4.26 × 10−3∕K. Tabelle I.4 gibt eine Zusammenfassung. Sie zeigt, dass auch bei ziemlich unterschiedlichen Debye-Temperaturen der Temperaturkoeffizient sich nicht sehr viel unterscheidet.
Bei Metallen, bei denen die obige Regel nicht so genau gilt, wird dies
zurückgeführt. Für Metall-Widerstandsthermometer werden Metalle mit hohem Temperaturkoeffizienten und guter Stabilität verwendet, so vor allem Pt, Ni, Ir und Mo. Normiert sind die PT-100 Widerstände, die beider Referenztemperatur auf 100 Ω normiert sind. Abb. 4.121 zeigt die typische Kennlinie eines Metallwiderstandes.
Bei Halbleitern ist neben der Temperaturabhängigkeit der Streuung vor allem die Konzentration sowohl der positiven wie auch der negativen Ladungsträger als Funktion der Temperatur wichtig. Aus der Gleichung (4.55)für die Leitfähigkeit von Metallen kann für Halbleiter die folgende Beziehung postuliert werden, indem man annimmt, dass die Leitung der positiven und negativen Ladungsträger unabhängig ist
![σ(T ) = q[n(T )μn(T) + p(T )μp(T)]](phys_elektr924x.png) | (4.62) |
Das Bändermodell in Abb. 4.122 stellt beispielhaft am Leitungsband und am Donatorenband dar, wie die Energielandschaft in der Bandlücke ist. Die Leitfähigkeit von Halbleitern setzt sich aus zwei Teilen, der Störstellenleitung
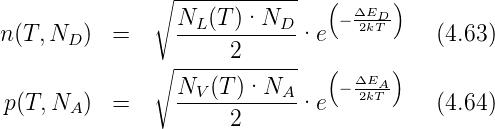
und der Eigenleitung
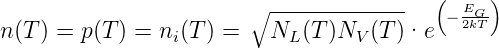 | (4.65) |
mit NL(T) = 2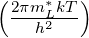
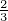 und NV (T) = 2
und NV (T) = 2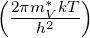
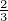 zusammen. In erster Näherung dominieren die exponentiellen
Boltzmann-Terme gegen die T3∕2 Abhängigkeit der
Vorfaktoren.
zusammen. In erster Näherung dominieren die exponentiellen
Boltzmann-Terme gegen die T3∕2 Abhängigkeit der
Vorfaktoren.
Es gibt im Widerstandsverhalten von Halbleitern drei Bereiche
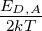 an.
an.
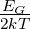 an.
an.Abb. 4.123 zeigt eine Skizze dieses Verhaltens.
Im mittleren Bereich, bei einer konstanten Ladungsträgerkonzentration, sollte sich die Leitfähigkeit wie T−3∕2 verhalten. Tatsächlich beobachtet man aber Exponenten zwischen -1.5 und -2.5. Thermowiderstände aus Silizium werden typischerweise zwischen 220 K und 420 K eingesetzt.
Der Spreading-Widerstand, dessen Kennlinie in Abb. 4.124 gezeigt ist, wird üblicherweise zur Messung des temperaturabhängigen spezifischen Widerstandes eingesetzt. Dabei handelt es sich um einen kreisförmigen, ebenen Kontakt mit dem Durchmesser d. Wenn d klein ist gegen die Dicke des Halbleitermaterials erhält man für den Spreading-Resistance
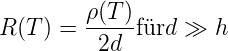 | (4.66) |
Heissleiter Die Leitungsmechanismen in Halbleitern sind anders als in Metallen. Bei gewissen halbleitenden Keramikwerkstoffen ergibt sich die Leitung durch das Hüpfen von Ladungsträgern von einem Korn zum nächsten. Diese keramischen Werkstoffe werden durch Sintern hergestellt. Dabei werden pulverförmige Materialien unter Druck soweit erhitzt, dass die einzelnen Pulverkörner zusammenbacken. Der Widerstand zwischen den Körnern ist dabei sehr viel grösser als in den Körnern. Durch das Vorhandensein dieser Barriere ist die Elektronenleitung ein thermisch aktivierter Prozess. Deshalb ist die Leitfähigkeit bei hohen Temperaturen besser ist als bei tiefen.
Viele Heissleiter sind nach der Strukturformel A2+B 23+O 42− aufgebaut. Dabei sind A zweiwertige und B dreiwertige Metalle. Die Metallkationen auf der position A werden tetraedrisch von 4 Sauerstoffanionen umgeben, während B oktaedrisch von 8 Sauertoffanionen umgeben ist. Diese Spinell-Struktur wird durch die Einlagerung von Oxiden so verändert, dass auf B zwei- und drei-wertige Metalle sitzen: damit kann ein Hopping-Prozess durchgeführt werden. Die Bewegung wird durch die Rate des Ablöse- und Einfang-Prozesses bestimmt. Sie wird analog zur Diffusion von Atomen in Festkörpern beschrieben
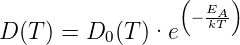 | (4.67) |
Mit der Einsteinbeziehung wird die Beweglichkeit
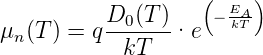 | (4.68) |
Unter Vernachlässigung des Vorfaktors ergibt sich
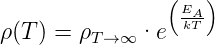 | (4.69) |
oder für eine vorgegebene Widerstandsgeometrie
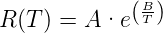 | (4.70) |
Hier wurden zwei Materialkonstanten A und B eingeführt. man kann sie bestimmen, indem man den Widerstandswert R für zwei feste Temperaturen bestimmt. Die eine dieser festen Temperaturen ist meistens T20 = 293, 15K, der dazugehörige Widerstandswert sei R20 = A exp(B∕T20). damit wird auch A = R20 exp(−B∕T20.
Die zweite feste Temperatur sei Tx mit dem Widerstandswert Rx. Daraus erhält man
![[ ( 1- -1-)]
Rx = R20e B Tx−T20](phys_elektr938x.png) | (4.71) |
Löst man diese Gleichung nach B auf, so ergibt sich
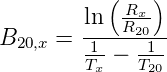 | (4.72) |
Damit ist es nun möglich, den Temperaturgang des Widerstandes anzugeben.
![[ ( )]
B20,x 1T−T1-
R (T ) = R20e 20](phys_elektr940x.png) | (4.73) |
Aus Gleichung (4.58) folgt für den temperaturabhängigen Temperaturkoeffizienten des Widerstandes
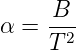 | (4.74) |
Heissleiter sind stark nichtlineare Widerstände. Ein typischer Widerstandsverlauf ist in Abb. 4.125 gezeigt. Damit kann man sie, zum Beispiel, als Übertemperatursicherungen verwenden, die direkt am Verbraucher die Versorgungsspannung teilweise kurzschliessen. Heissleiter sind über die Materialzusammensetzung sehr leicht auf einen bestimmten Grundwiderstand und einen gewünschten Temperaturverlauf einstellbar. Typische Heissleitermaterialien sind Fe3O4, Zn2TiO4 und viele andere mehr.
Abb. 4.126 zeigt die Kennlinie eines Kaltleiters.
Diese bestehen aus Mischkristallen und Metalloxiden,
wie zum Beispiel BaO, CaO, SrO, ZrO2. Die Kaltleiter
sind ferroelektrisch. Viele dieser Keramiken haben eine
Perowskitstruktur (wie die Hochtemperatursupraleiter)
mit der Strukturformel A2+B4+O
36−. Dabei wird die
A-Position durch zweiwertige Metalle mit Oxiden des
Typs AO besetzt. Die B- Position muss mit vierwertigen
Metallen und damit den Oxiden des Typs BO2 besetzt
werden. Der Stromfluss in diesen Materialien wird durch die
Potentialbarrieren an den Korngrenzen bestimmt. Die dort als
Akzeptoren chemisorbierten Sauerstoffatome[Kul81] führen zu
Verarmungszonen der Weite w. Diese ergibt sich aus aus der
Anzahl besetzter Sauerstoffplätze NS und der Dotierung n
D
zu
und der Dotierung n
D
zu
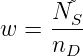 | (4.75) |
Aus der Poissongleichung berechnet man die Potentialhöhe Ψ0 der Barriere.
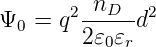 | (4.76) |
Der elektrische Widerstand zeigt deshalb eine exponentielle Abhängigkeit von der Temperatur
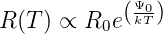 | (4.77) |
Der elektrische Widerstand eines Kaltleiters steigt bei der Curie-Temperatur des Ferroelektrikums abrupt an. Unterhalb der Curie-Temperatur gibt es in den einzelnen Körnern spontane Polarisation. Die negative Korngrenzenladung wird dadurch abgeschirmt. Damit verringert sich bei tiefen Temperaturen (unter der Curie-Temperatur) die Potentialbarrieren zwischen den Körnern. Oberhalb der Curie-Temperatur ist die Dielektrizitätszahl sehr viel geringer als unterhalb. Oberhalb existiert keine ferroelektrische Ordnung und keine spontane Polarisation. Die Abschirmung der Raumladungszonen wird sehr viel ineffektiver, die Potentialbarrieren steigen. damit steigt auch der Widerstand beim Übergang von tiefen zu hohen Temperaturen um 3 bis 6 Grössenordnungen. Der weiteren Zuname wirken die an Korngrenzen bei hohen Temperaturen freigesetzten Ladungsträger entgegen.
Integrierte Temperatursensoren Die Temperaturabhängigkeit des Stromes durch pn-Übergänge oder die Temperaturabhängigkeit der Spannung an solchen Übergängen lässt sich zur Temperaturwmessung ausnutzen.
Nach Shockley ist die Strom-Spannungskennlinie einer p+n-Diode
dabei ist IS der Sättigungsstrom und Dp die Diffusionskonstante
der Ladungsträger. Näherungsweise ist die Leitfähigkeit eine
exponentielle Funktion von −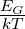 .
.
Mit Gleichung (4.65) erhält man für den Strom durch eine in Flussrichtung betriebene Diode
mit der Nebenbedingung Uf »kT∕q. Da der Strom If ebenfalls temperaturabhängig ist, erhält man die folgende nichtlineare Kennlinie
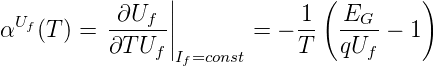 | (4.82) |
In der Praxis verwendet man als Sensor anstelle einer Diode die Basis-Emitter-Strecke eines Transistors, bei dem Kollektor und Basis kurzgeschlossen sind. Diese Anordnung hat eine Charakteristik, die sehr viel besser mit der Shockley-Gleichung beschrieben werden kann als die einer Diode.
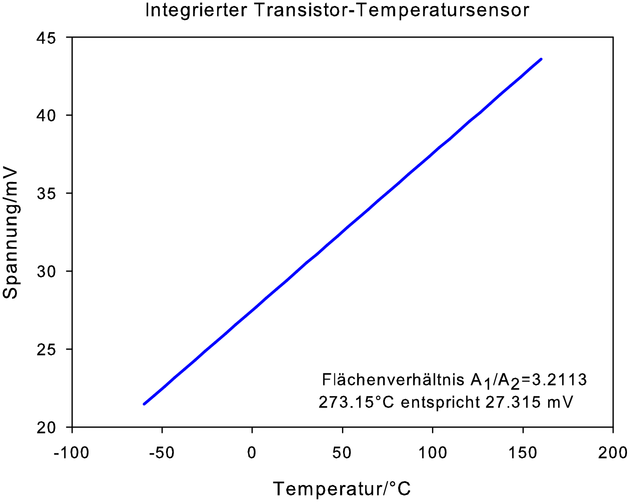
| Abbildung 4.127.: | Kennlinie eines integrierten Temperatursensors. Das Flächenverhältnis ist so eingestellt, dass die resultierende Spannung in mV ein Zehntel der Temperatur in K ist. Die Temperaturablesung mit einem digitalen Voltmeter wird dann sehr einfach. |
Abb. 4.127 zeigt die Temperaturabhängigkeit der Basis-Emitterspannungsdifferenz zweier gekoppelter Transistoren. Das Verhältnis der Stromabhängigkeit von zweier auf dem gleichen Chip hergestellter Transistoren ist einfach das Verhältnis ihrer Basisflächen A1 und A2. Man erhält in sehr guter Näherung, sofern die Flächen nicht gleich sind, die lineare Kennlinie
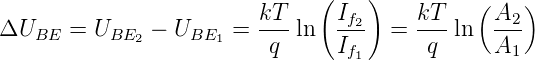 | (4.83) |
Wählt man A2∕A1 = 3.2113 ist ΔUBE = 0.1(mV∕0C)·T.
Wenn über einem Leiterstück der Länge l die Temperatur ΔT abfällt, dann entsteht die Thermospannung
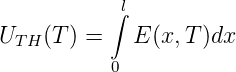 | (4.84) |
Bei homogenen Materialien definiert man den Seebeck-Koeffizienten αS. Die Thermospannung ist dann
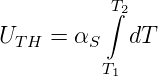 | (4.85) |
Bei der hochohmigen Messung der Thermospannung nach Abb. 4.128 muss man zwei Materialien A und B mit unterschiedlichen Seebeck-Koeffizienten einsetzen. Man erhält
Die Wahl der Materialien von Thermopaaren hängt vom Temperaturbereich, der verlangten Genauigkeit und nicht zuletz auch vom Preis ab. Tabelle I.3 im Anhang zeigt die thermoelektrische Spannungsreihe und die Seebeck-Koeffizienten.
Abbildung 4.129 zeigt die Messanordnung der Temperatur mit einem Pyroelektrikum. In gewissen unsymmetrisch aufgebauten Kristallen (Triglyzinsulfat (TGS), Lithiumtantalat, Blei-Zirkonat-Titanat (PZT) und PVDF-Folien) mit polarer Achse können spontane elektrische Polarisationen auftreten. Die Änderung der elektrischen Polarisation aufgrund der Änderung der Temperatur nennt man den pyroelektrischen Effekt. Zusätzlich werden Oberflächenladungen erzeugt.
Mit den pyroelektrischen Koeffizienten 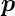 (T) und unter der
Annahme kleiner Temperaturänderungen (
(T) und unter der
Annahme kleiner Temperaturänderungen (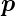 (T) ≈
(T) ≈ 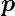 T )
bekommt man für die Polarisation
T )
bekommt man für die Polarisation
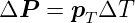 | (4.89) |
ist das Dielektrikum geeignet orientiert, das heisst, nur die x-Achse ist involviert, erhält man
Um den Einfluss der Kriechströme auf die Ladungsmessung zu minimieren, muss die Wärmestrahlung zerhackt werden. Da alle Pyroelektrika auch Piezoelektrika sind, muss beim experimentieren geachtet werden, dass man nicht den Piezoeffekt fälschlicherweise für den pyroelektrischen Effekt hält.
Licht kann durch seine thermischen, energetische oder mechanischen Wirkungen gemessen werden. Thermische Wirkungen nutzt man aus, wenn die aus Licht absorbierte Wärmemenge (zum Beispiel bei einem Bolometer) oder die absorbierte Leistung (zum Beispiel ein Schwarzer Körper mit einem definierten Wärmeleck an die Umgebung) zu einer Temperaturerhöhung führt, die dann wie im Kapitel 4.2.4 gemessen werden kann.
Licht hat eine Energiedichte, das heisst, ein federnd gelagerter Spiegel wird durch den der Energiedichte äquivalenten Druck ausgelenkt. Dieser Effekt hat nur bei sehr präzisen Messungen oder sehr kleinen Spiegeln einen Einfluss.
Meistens wird Licht über den äusseren oder den inneren Photoeffekt detektiert. Mit dem äusseren Photoeffekt bezeichnet man die Anregung von Ladungsträgern aus dem Leitungs- oder Valenzband über die Vakuumenergie hinaus, wie es in Abb. 4.130 schematisch dargestellt ist. Dass Metalle stabil sind hängt damit zusammen, dass die Fermi-Energie um eine Austrittsarbeit ΦA genannte Energie unter dem Vakuumenerginiveau liegt. Bei den Halbleitern kommt noch die Elektronenbindungsenergie ϕ hinzu, die den Abstand der Valenzbandoberkante von der Fermi-Energie EF beschreibt. Folgende Ungleichung
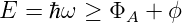 | (4.92) |
muss erfüllt sein. Wir können die kinetische Energie der Elektronen Ekin oder das dazu äquivalente Potential Ue ausrechnen.
Schliesslich ergibt sich für die langwellige Grenze
![λ = -h-·c---= ---1.24μm-----
G ΦA + ϕ (ΦA + ϕ) [eV ]](phys_elektr961x.png) | (4.95) |
Die Fotokathoden sind demnach nur bis zu einer bestimmten Wellenlänge empfindlich. Je länger die noch zu detektierende Wellenlänge sein soll, desto niedriger muss die Austrittsarbeit des Kathodenmateriales sein. Häufig werden für den sichtbaren Bereich CsSb und Na/K/Sb- Verbindungen verwendet.
Abb. 4.131 zeigt links den Aufbau einer Fotozelle. Die durch das Licht aus der Fotokathode K herausgelösten Elektronen werden durch die Spannung zur Anode hin beschleunigt. der entstehende Strom wird als Spannungsabfall über dem Widerstand R gemessen. Um Stösse der Elektronen zu vermeiden muss der Raum zwischen Fotokathode und Anode evakuiert sein. Die spektrale Empfindlichkeit hängt vom verwendeten Kathodenmaterial ab. Im Durchschnitt werden für jedes absorbierte Photon etwa 0.1 Elektronen emittiert. Um einen Strom von 1 pA zu bekommen, müssen also 10−12∕(1.6 × 10−19) = 6.25 × 107 Photonen absorbiert werden, was bei einer Photonenenergie von 2 eV einer Lichtleistung von 20 pW entspricht. Da es schwierig ist kleinere Ströme zu messen, ist dies die praktische Grenze der Empfindlichkeit.
Um auch einzelne Photonen detektieren zu können verwendet man Photovervielfacher (Photo Multiplier), wie in Abb. 4.131 gezeigt. Dabei werden die emittierten Photoelektronen über eine Spannung von etwa 100 V beschleunigt und auf eine Zwischenelektrode geschickt. Ihre kinetische Energie bewirkt, dass mehr al 1 Elektron, im allgemeinen υ Elektronen, für jedes eintreffende Elektron freigesetzt werden. Die von der Anode aufgefangene Elektronenzahl ist für n solcher Verstärkungsstufen υn. Bei 10 Stufen und einem υ = 4.78 würde für jedes Photon 6250000 Elektronen erzeugt.
da bei einer Photozelle oder einem Photovervielfacher nur sehr kleine Kapazitäten vorkommen, können Frequenzen bis zu 10 GHZ detektiert werden. dabei ist zu beachten, dass die Laufzeiten im Detektor einige Nanosekunden betragen können.
Abb. 4.132 zeigt das Bändermodell für den innern Photoeffekt. Neben der Anregung vom Valenzband ins Leitungsband mit der Energie grösser als Eg können auch Anregungen vom Valenzband in Fremdatomzustände (Energie EA) oder von von Fremdatomzuständen ins Leitungsband (hier auch mit EA) auftreten.
Bei einem Photowiderstand ändert sich sein Leitwert mit der Anzahl vorhandener Ladungsträger. Wenn das Licht vollständig absorbiert wird, der Quantenwirkungsgrad η, die Strahlungsleistung P, der Querschnitt des Widerstandes A und seine Länge l sind, ist die Rate, mit der Ladungsträger ins Leitungsband angeregt werden
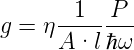 | (4.96) |
Die Rekombinationsrate r hängt von der mittleren Lebensdauer τ und der Ladungsträgerkonzentration n ab
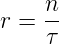 | (4.97) |
Im Gleichgewicht ist die Rekombinationsrate r gleich der Generationsrate g. Die Anzahl Ladungsträger im Leitungsband ist also
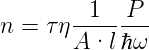 | (4.98) |
Andererseits kann man für den Strom im Halbleiter bei bekannter Beweglichkeit μn schreiben
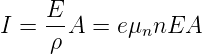 | (4.99) |
Die Kombination von Gleichungen (4.98) und (4.99) gibt
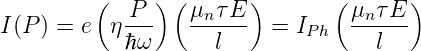 | (4.100) |
Die Transitzeit (Zeit zum Durchqueren des Widerstandes)
sei ttr = 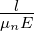 . Dann ist der Verstärkungsfaktor
. Dann ist der Verstärkungsfaktor
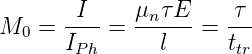 | (4.101) |
und hängt nur vom Verhältnis der mittleren Ladungsträgerlebensddauer und zur Transitzeit zwischen den Elektronen ab.
Die spektrale Empfindlichkeit eines Photoleiters basierend auf dem inneren Photoeffekt ist
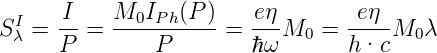 | (4.102) |
Die Empfindlichkeit steigt also linear mit der Wellenlänge an, solange die Grenzwellenlänge, die durch die minimalen Energiesprünge gegeben ist, nicht erreicht werden. Photoleiter haben demnach ein ideales Quantenverhalten. Sie werden für das sichtbare Licht aus CdSe und CdS und für den infraroten Bereich aus PbS, PbSe, PbTe und InSb hergestellt.
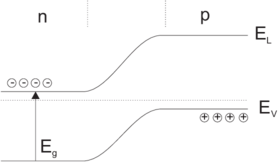
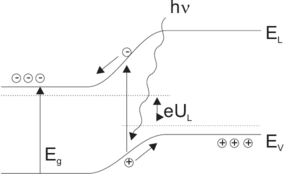
| Abbildung 4.133.: | Bändermodelle für den inneren Fotoeffekt: links unbeleuchtet und rechts beleuchtet. |
In der Raumladungszone eines pn-Überganges entstehen bei der Beleuchtung Elektron-Loch-Paare. Wie die linke Seite von Abb. 4.133 zeigt, werden die Elektronen zur n-Zone und die Löcher zur p-Zone beschleunigt. Dadurch nimmt die elektrische Feldstärke in der Raumladungszone und damit auch die Barrierenhöhe ab. Die Fermienergien verschieben sich, es entsteht eine elektromotorische Kraft. Diese wird als fotovoltaische Spannung UL aussen abgegriffen.
Der generierte Fotostrom ist
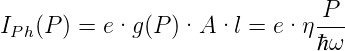 | (4.103) |
Analog ist die spektrale Empfindlichkeit (siehe auch Abb. 4.134)
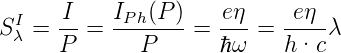 | (4.104) |
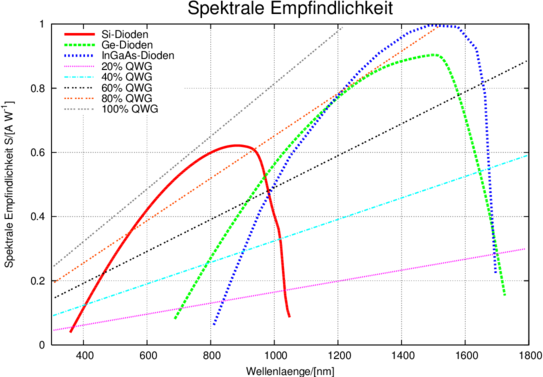
| Abbildung 4.134.: | Spektrale Empfindlichkeit von verschiedenen Materialien im Vergleich zu Quanteneffizienzen. |
Anders als bei Photowiderständen gibt es hier keinen durch die aussen angelegte Spannung bedingten Verstärkungsfaktor M0. Photodioden sind deshalb schneller und weniger empfindlich. Da die Raumladungszone eine sehr geringe Tiefe l hat, muss der Quantenwirkungsgrad η als wellenlängenabhängig angenommen werden.
Wird die Photodiode in Sperrichtung vorgespannt, dann ist der Potentialverlauf in der Raumladungszone steiler, entsprechend werden die von Licht generierten Ladungsträger schneller zu den Anschlüssen befördert: die Photodiode wird schneller. Wird die Vorspannung so gross, dass die Energie der vom Licht generierten Ladungsträger ausreicht, weiter Ladungsträger zu generieren (Avalanche-Effekt oder Lawineneffekt) dann hat die dann Avalanche-Photodiode genannte Diode eine innere Verstärkung, die in besonderen Fällen zum Zählen einzelner Photonen ausreicht.
Die Strom-Spannungskennlinie (siehe Abb. 4.135) einer Photodiode lässt sich analog zu der einer gewöhnlichen Diode als
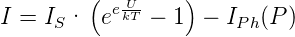 | (4.105) |
Je nach äusserer Beschaltung betreibt man die Photodiode als Photodiode (Abb. 4.136, links) oder als Photoelement (Abb. 4.136, links). Die Photodiode arbeitet im 3. Quadranten des Kennlinienfeldes in Abb. 4.135, das Photoelement im vierten. Die Beschaltung mit einem Widerstand R ist in Abb. 4.136 eingezeichnet. Der Schnittpunkt der jeweiligen Arbeitsgeraden mit der Widerstandskennlinie ergibt den Arbeitspunkt. Als Material für Photodioden wird bevorzugt Si verwendet, für den Infrarotbereich auch Ge und InSb.
Abb. 4.137 zeigt, wie man die Empfindlichkeit einer Photodiode steigern kann, indem man sie als Stromquelle an der Basis eines Transistors verwendet. Die linke Seite zeigt einen Querschnitt durch einen Phototransistor, der sich von einem gewöhnlichen Transistor durch seinen grösseren Basis-Emitterbereich unterscheidet. Wenn der Transistor die Stromverstärkung β hat so ist der Kollektorstrom
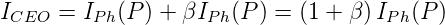 | (4.106) |
Entsprechend ist die spektrale Empfindlichkeit
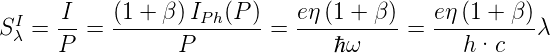 | (4.107) |
 Lizenzinformationen
Lizenzinformationen