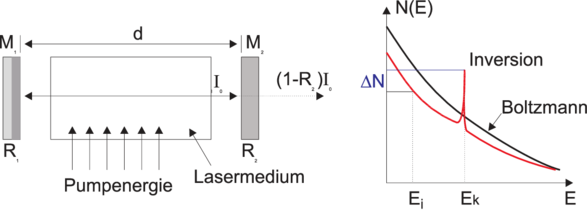
| Abbildung 4.199.: | Aufbau eines Lasers (links) sowie schematische Darstellung der Inversion im Vergleich zur thermischen Verteilung. |

Optische Messverfahren werden in der modernen Laborpraxis immer wichtiger. Sie ermögliche eine extrem hohe zeitliche und spektrale (energetische) Auflösung. Licht wird auf seinem Weg durch andere elektromagnetische Strahlung nicht beeinflusst, sofern die Intensitäten klein genug sind, dass keine nichtlinear-optischen Effekte auftreten.
Im folgenden Abschnitt wird auf die Grundlagen der Lasertechnik eingegangen. Es folgt eine Darstellung von Systemen zur Erzeugung ultrakurzer Pulse. Diese werden einerseits mit Pump-Probe-Techniken und andererseits mit elektrooptischen Verfahren detektiert. Schliesslich werden Geräte zur Messung von Spektren besprochen.

| Abbildung 4.199.: | Aufbau eines Lasers (links) sowie schematische Darstellung der Inversion im Vergleich zur thermischen Verteilung. |
Wenn sich Materie in optisch angeregten Zuständen befindet, wird diese Anregung durch Emission abgebaut. Wenn es gelänge, alle Atome oder Moleküle in einem bestimmten Volumen kohärent strahlen zu lassen, dann würde man eine Lichtquelle mit einzigartigen Eigenschaften gewinnen.
Der Laser, am Anfang der 60-er Jahre erfunden wurde, erfüllt genau diese Bedingungen. Die Abbildung 4.199 zeigt den schematischen Aufbau. Ein aktives Medium befindet sich in einem Fabry-Perot-Resonator[Pér96a][Dem93]. Das Licht im Resonator wird durch das aktive Medium bei jedem Durchgang verstärkt. Die Verstärkung erfolgt durch stimulierte Emission. Ein kleiner Teil des Lichtes wird durch die Spiegel des Fabry-Perot-Resonators ausgekoppelt und steht für Experimente zur Verfügung.
Die rechte Seite der Abb. 4.199 zeigt die Besetzungsverteilung. Im Vergleich zu einer thermischen Verteilung, gegeben durch die Boltzmannverteilung N(E) = exp(−E∕kT), sind die Zustände bei hohen Energien deutlich stärker besetzt als im thermischen Fall. Diese sogenannte Besetzungsinversion ist für die Funktionsweise des Lasers notwendig.
Die Diskussion der Wirkungsweise von Lasern beruht auf dem exzellenten Lehrbuch von Demtröder[Dem93].
Um die Intensität der in z-Richtung laufenden Welle in Abb. 4.200 zu berechnen setzen wir für die Intensität an
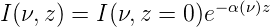 | (4.1) |
I(ν,z = 0) ist dabei die Refernzintensität bei z = 0.
Hier ist der frequenzabhängige Absorptionskoeffizient durch
![α(ν) = [Ni − (gi∕gk)Nk ]σ(ν)](phys_elektr1187x.png) | (4.2) |
gegeben. αν hängt von den Besetzungsdichten Ni des unteren Laserniveaus und Nk des oberen Laserniveaus, von den statistischen Gewichten gi und gj23 und vom optischen Wirkungsquerschnitt σν ab.
Wenn (gi∕gk)Nk > Nk ist, wird der Absorptionskoeffizient in Gleichung (4.2) negativ. Aus der Dämpfung ist also, analog wie bei der Phasendrehung von Operationsverstärkern, eine Verstärkung geworden. Der Verstärkungsfaktor ist
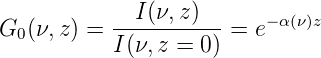 | (4.3) |
Die gesamte Abschwächung oder, bei negativen Werten von γ kann in eine Gleichung mit einem Exponentialfaktor zusammengefasst werden.
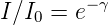 | (4.4) |
In der Regel wird das zur Verstärkung verwendete optische Medium in einen Resonator gebracht (analog zur Abb. 4.200, links). An den beiden Endspiegeln treten Verluste auf. Einerseits ist es nicht möglich, einen Spiegel mit einer Reflektivität von 100% zu bauen, der zudem noch eine unendliche Ausdehnung hat um Beugungsverluste zu minimieren. Andererseits muss an einem Spiegel die Reflektivität kleiner als 1 sein, damit Laserlicht ausgekoppelt werden kann. Die Verstärkung, Beugungs-, Auskopplings- Reflexionsverluste beim beim Durchgang durch einen Resonator können als Intensitätsänderung pro Umlauf geschrieben werden
![G = I∕I0 = exp [− 2α (ν )L − γ]](phys_elektr1190x.png) | (4.5) |
Bei der Berechnung der Verstärkung nach einem Umlauf ist angenommen worden, dass das Medium die Länge L hat. Wenn G grösser als 1 ist, beginnt die stimulierte Emission im Lasermedium die spontane Emission zu dominieren. Damit dies möglich ist, muss −2α(ν)L > γ sein. Zusammen mit Gleichung (4.2) bekommt man die Schwellwertbedingung
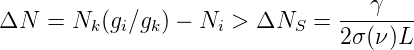 | (4.6) |
für die minimale Besetzungsinversion ΔNS.
Die Laseremission beginnt immer mit einer spontanen Emission aus dem oberen Laserniveau in eine Resonatormode. Dabei werden die Photonen, deren Frequenz nahe der Resonator-Mittenfrequenz liegt, bevorzugt verstärkt. Durch die beginnende stimulierte Emission wird wird die Besetzungsinversion abgebaut bis ein Gleichgewicht erreicht wird. Unabhängig von der Pumpleistung ist die Inversion in einem Laser beim stationären Betrieb immer gleich der Schwellwertinversion ΔNS.
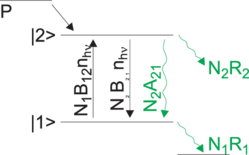
| Abbildung 4.201.: | Funktion eines Lasers: Pumpprozess P, Relaxationsraten, induzierte und spontane Emission. |
Der stationäre Laserbetrieb kann durch Bilanzengleichungen beschrieben werden. Anhand des Termschemas in Abb 4.201 ist ersichtlich, dass aus einem Pumpprozess P das obere Laserniveau |2 > gespiesen wird. Zusätzlich wird die Besetzungszahl dieses Niveaus durch die Absorption aus dem unteren Laserniveau |1 > mit der Rate N1B12·n·h·ν erhöht. Es gibt drei Verlustkanäle, die spontane Emission mit der Rate N2A21, die induzierte Emission mit der Rate N2B21·n·h·ν und die verlustrate N2R2, zum Beispiel in Triplettzustände. Das untere Laserniveau |1 > wird durch den Relaxationsprozess mit der Rate N1R1 entvölkert.
Wenn man annimmt, dass die statistischen Gewichte gleich sind (g1 = g2), bekommt man die Ratengleichungen
Der Laserresonator hat seine eigene Verlustrate. Wenn man N1 = N2 setzt erhält man aus (4.9) den Verlustfaktor β
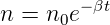 | (4.10) |
Durch Vergleich erhält man für den Verlustfaktor γ
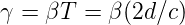 | (4.11) |
wobei d die Resonatorlänge ist.
Im stationären Betrieb müssen die in den obigen Gleichungen vorkommenden Ableitungen verschwinden. Aus den Gleichungen (4.7) und (4.8) bekommt man in diesem Falle
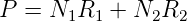 | (4.12) |
Die Pumprate muss also im stationären Betrieb die beiden Verlustraten N1R12 und N2R2 aus dem unteren, beziehungsweise aus dem oberen Laserniveau ausgleichen. Andererseits bekommt man durch Addition aus (4.8) und (4.9) die Gleichung
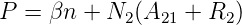 | (4.13) |
Die Pumprate P ersetzt also die Resonatorverluste (4.11) sowie die durch spontane Emission und Relaxation aus dem oberen Laserniveau verschwindenden Photonen. Die Relaxationsrate des unteren Niveaus ist im stationären Betrieb
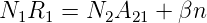 | (4.14) |
Sie kompensiert gerade die spontane Emission und die Verlustrate der induzierten Photonen. Deshalb ist sie immer grösser als die Auffüllrate aus dem Niveau |2 > durch spontane Emission.
Wir multiplizieren Gleichung (4.7) mit R2 und Gleichung (4.8) mit R1 und können für den stationären Zustand (d∕dt = 0) mit der Definition ΔNstat = N2 −N1 die folgende Umformung
durchführen.
Mit der Gleichung (4.12) erhält man die stationäre Besetzungsinversion
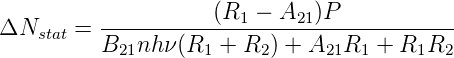 | (4.16) |
Aus (4.16) folgt, dass eine stationäre Besetzungsinversion ΔNstat > 0 nur für Medien mit R1 > A21 möglich ist. Dies bedeutet, dass das untere Laserniveau sich schneller entleeren muss als das obere sich durch spontane Emission entvölkert.
Im realen Laserbetrieb wird das untere Laserniveau zusätzlich durch die induzierte Emission bevölkert. Die Relaxationsrate des unteren Laserniveaus muss deshalb der Bedingung
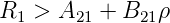 | (4.17) |
genügen.
Wenn der Energieverlust der k-ten Mode mit der Zeit wie
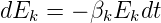 | (4.18) |
ist dann ist
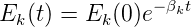 | (4.19) |
Die Resonatorgüte ist als
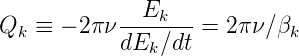 | (4.20) |
definiert. Für einen Resonator der Länge d ist der Verlustfaktor durch
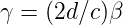 | (4.21) |
gegeben. Der Verlustfaktor setzt sich aus Beugungsverlusten, Absorptionsverlusten, Reflexionsverluste und die Verluste durch Lichtstreuung zusammen.
Intensität und Reflexionsverluste
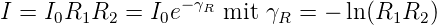 | (4.22) |
Mit der Umlaufzeit T = 2d∕c wird die Abklingkonstante βR = γR∕T = γR·c∕2d. Die mittlere Verweilzeit der Photonen im Resonator ist
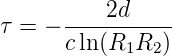 | (4.23) |
Die Beugung wird durch die Fresnel-Zahl charakterisiert.
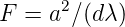 | (4.24) |
Sie gibt an, wieviele Fresnelzonen auf dem gegenüberliegenden Spiegel entstehen, wenn man im Abstand ρq = qλ∕d (q ganzzahlig). Wenn d < z0 ist, ist F > 1 und die Beugungsverluste minimal. Damit bei planparallelen Spiegeln ein Photon m-Umläufe machen kann, muss der Beugungswinkel Θ < a∕(md) sein. Also muss
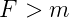 | (4.25) |
sein. Resonatoren mit der gleichen Fresnelzahl haben die gleichen Verluste.

| Abbildung 4.204.: | Anschauliche Erklärung, dass ein ebener Spiegelresonator mit einer Folge von Blenden äquivalent ist. |
Um die Beugungsverluste eines Resonators zu berechnen, kann man den Resonator durch eine Folge von Linsen und Blenden ersetzen (siehe Abb. 4.204). Dabei entsprechen ebene Spiegel einer Apertur. Gekrümmte Spiegel müssen entsprechend durch Sammel- oder Zerstreuungslinsen ersetzt werden. Aus der Abbildung 4.204 ist sofort ersichtlich, dass ebene Wellen keine Lösung des resonatorproblems sein können.
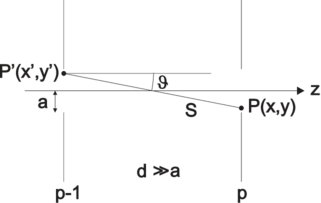
| Abbildung 4.205.: | Die Feldamplitude P(x,y) kann aus den Amplituden in der Ebene P′(x′,y′) bestimmt werden. |
Um die Beugungserscheinungen an einer Folge von Aperturen handhaben zu können, wird die Kirchhoff-Fresnel’sche Beugungstheorie auf die Geometrie in Abb. 4.204. Die Feldverteilung bei der Ap-ten Apertur wird aus der Feldverteilung in der Ap−1-ten Apertur mit Hilfe der Gleichungen der Fourieroptik berechnet.
Die Amplitude am Punkt P(x,y) in der Apertur Ap ist durch
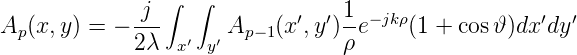 | (4.26) |
gegeben (Siehe Abb. 4.205). Die stationäre Feldverteilung muss die beiden folgenden Eigenschaften haben:
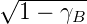 < 1 aus.
< 1 aus.
Für die Amplitude gilt also
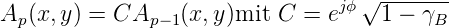 | (4.27) |
wobei wie oben diskutiert, der Faktor 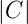 2 = 1 −γ
B
den ortsunabhängigen Intensitätsverlust durch Beugung
beschreibt. Die Modenverteilung ist die Lösung der Gleichung,
die entsteht, wenn man (4.27) in (4.26) einsetzt. Diese
Gleichungen sind im allgemeinen nicht analytisch lösbar.
2 = 1 −γ
B
den ortsunabhängigen Intensitätsverlust durch Beugung
beschreibt. Die Modenverteilung ist die Lösung der Gleichung,
die entsteht, wenn man (4.27) in (4.26) einsetzt. Diese
Gleichungen sind im allgemeinen nicht analytisch lösbar.
Nur für den symmetrischen konfokalen Resonator kann eine Näherungslösung[Dem93] angegeben werden. Dazu muss der Ursprung des Koordinatensystems in das Zentrum des Resonators gelegt werden. Dann ist für eine beliebige Ebene die Intensitätsverteilung
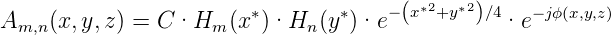 | (4.28) |
Hm und Hn sind die Hermitschen Polynome m-ter
und n-ter Ordnung. C ist ein Normierungsfaktor und
x∗ = 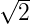
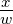 und y∗ =
und y∗ = 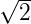
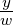 sind normierte Koordinaten.
Die Normierungsgrösse w ist ein Mass der radialen
Amplitudenverteilung und durch
sind normierte Koordinaten.
Die Normierungsgrösse w ist ein Mass der radialen
Amplitudenverteilung und durch
![[ ( ) ]
2 λd- 2z- 2
w (z) = 2 π 1 + d](phys_elektr1218x.png) | (4.29) |
gegeben. d ist hier die Länge des Resonators. Unter Verwendung der Abkürzung ξ = 2z∕d bekommt man für die Phase
![[ ] ( )
2π- b-( 2) (x2-+-y2)ξ- π- 1-−-ξ-
ϕ(x,y, z) = λ 2 1 + ξ + d(1 + ξ2) − (1+m+n ) 2 − arctan 1 + ξ](phys_elektr1219x.png) | (4.30) |
Abbildung 4.206 zeigt einige Modenverteilungen. Sie werden TEM-Moden genannt, da sie in guter Näherung transversal-elektromagnetische Wellen darstellen. Die Zahlen m und n geben die Anzahl Knoten der Feldverteilung an.
Ist n = m = 0 so hat man die Grundmode. Ihre Intensitätsverteilung ist
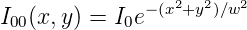 | (4.31) |
Sie haben deshalb eine Gausssche Intensitätsverteilung. Die Grösse w gibt an, bei welchem Radius die Intensität auf den Faktor 1∕e2 bezogen auf das Strahlzentrum abgefallen ist. Der minimale Strahldurchmesser
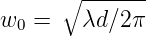 | (4.32) |
heisst auch Strahltaille. Eine exemplarische Amplitudenverteilung ist in der Abbildung 4.207 gezeigt. Rsonatoren, deren Spiegel sich in die Wellenfronten eines symmetrischen konfokalen Resonators einpassen lassen, können ebenfalls mid der hier gezeigten Theorie beschrieben werden.
Die Abbildung 4.208 zeigt Beispiele von Laserresonatoren.
Die Beugungsverluste von offenen Resonatoren hängen von der betrachteten Lasermode ab. Abbildung 4.209 zeigt einen Graphen der Beugungsverluste. Als Ordinate ist die Fresnel-Zahl angegeben. Durch eine Verringerung der Fresnel-Zahl können die Verluste der höheren Modenordnungen so vergrössert werden, dass sie nicht mehr anschwingen können.
Die Stabilität eines Resonators folgt aus der Forderung, dass die Strahlparameter eines zu den Spiegeln passenden Gaussstrahls nach einem Umlauf auf sich selber abgebildet werden soll. Aus der Mathematik der Gaussstrahlen erhält man mit
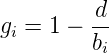 | (4.33) |
den Durchmesser des Strahls auf den Spiegeln M1 und M2. Der Strahldurchmesser ist jeweils
Also divergieren die Strahldurchmesser für g1g2 = 1 sowie für g1 = 0 und g2 = 0. Die Stabilitätsbedingung folgt aus (4.34) und (4.35) und ist
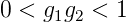 | (4.36) |
Das resultierende Stabilitätsdiagramm ist in der Abbildung 4.210 gezeigt. Eine Liste der Bezeichnungen zeigt Tabelle 4.10.
| Typ | Spiegelradien | Stabilitätsparameter |
| konfokal | b1 + b2 = 2d | g1 + g2 = 2g1·g2 |
| konzentrisch | b1 + b2 = d | g1·g2 = 1 |
| symmetrisch | b1 = b2 | g1 = g2 = g |
| symmetrisch konfokal | b1 = b2 = d | g1 = g2 = 0 |
| symmetrisch konzentrisch | b1 = b2 = 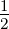 d d | g1 = g2 = −1 |
| semikonfokal | b1 = ∞, b2 = 2d | g1 = 1, g2 = 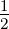 |
| eben | b1 = b2 = ∞ | g1 = g2 = +1 |
| Tabelle 4.10.: | Klassifizierung von Resonatoren nach Demtröder[Dem93]. Die bi sind die Krümmungsradien der Spiegel, deren Abstand d ist. |
Instabile Resonatoren, wie sie in der Abbildung 4.211 gezeigt sind, werden bevorzugt bei Verstärkermedien mit sehr hoher Verstärkung verwendet. Ebenso werden sie oft bei Kurzpuls-Lasern eingesetzt. Dadurch dass der Strahl divergiert, ist die Intensitätsverteilung des Laserlichts gleichmässiger über alle Moden verteilt.
Die Frequenzen der in einem Resonator möglichen Moden hängen, wie in Abbildung 4.212 gezeigt, vom Resonatortyp an. Beim konfokalen Resonator sind die Eigenfrequenzen durch
![[ ]
c- c-- 1-
ν = λ = 2d q + 2(m + n + 1)](phys_elektr1227x.png) | (4.37) |
gegeben. q ist der Index der longitudinalen Modenverteilung, m und n die Indices der transversalen Modenverteilung. Der Spiegelabstand
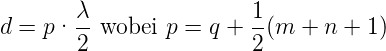 | (4.38) |
Das heisst, dass höhere transversale Moden mit q1 = q und q2 = m + n die gleich Frequenz haben wie eine transversale Grundmode (m + n = 0) mit dem longitudinalen Modenindex q = q1 + q2. Das Frequenzspektrum eines konfokalen Resonators ist also entartet. Der Modenabstand für die longitudinalen Moden ist
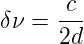 | (4.39) |
während transversale Moden mit q1 = m + n und q2 = q1 + 1 um
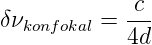 | (4.40) |
voneinander entfernt sind.
Bei nichtkonfokalen Resonatoren, bei denen der Krümmungsradius der Spiegel b nicht gleich dem Spiegelabstand d ist, ist das Frequenzspektrum nicht mehr entartet
![c [ 1 ( 4 d − b) ]
ν = --- q + --(1 + m + n ) 1 + --arctan -----
2d 2 π d + b](phys_elektr1231x.png) | (4.41) |
Die transversalen Moden liegen in einem Bereich um die transversale Grundmode mit dem gleichen longitudinalen Modenindex. Dies ist in der rechten Seite von Abbildung 4.212 gezeigt.
Bei einer endlichen Güte des Laserresonators verringert sich
die Intensität des Lichtes mit jedem Umlauf um einen kleinen
Wert. Nach der Zeit τ = 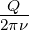 ist sie auf den Wert 1∕e
gesunken. Die daraus resultierende Frequenzunschärfe
ist
ist sie auf den Wert 1∕e
gesunken. Die daraus resultierende Frequenzunschärfe
ist
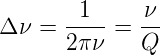 | (4.42) |
oder, umgeschrieben,
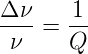 | (4.43) |
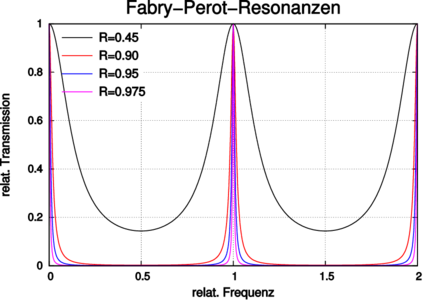
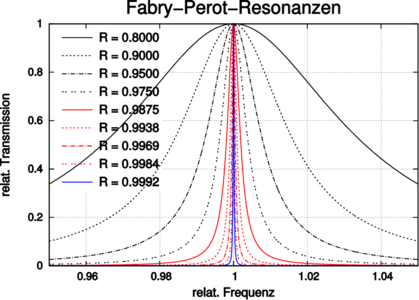
| Abbildung 4.213.: | Fabry-Perot-Resonanzen: oben ist ein Überblick gezeigt, unten die Vergrösserung um 1. Die Kurven sind auf einen Frequenzabstand von 1 normiert. |
Wenn die Verluste im Laserresonator vorwiegend durch die Auskopplung von Licht an den Spiegeln stammen, können die Gleichungen für Fabry-Perot-Interferometer verwendet werden. Dort ist die transmittierte Intensität durch
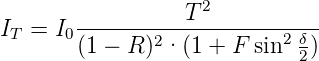 | (4.44) |
gegeben (siehe auch Abb. 4.213), wobei die Finesse
F = 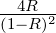 ist. Die Reflektivität R der Spiegel, die Absorption
A in den Spiegeln und ihre Transmission hängen über
T = 1 −A −R zusammen. Die Intensität im Resonator ist
Iint =
ist. Die Reflektivität R der Spiegel, die Absorption
A in den Spiegeln und ihre Transmission hängen über
T = 1 −A −R zusammen. Die Intensität im Resonator ist
Iint = 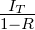 . Resonanzen treten bei δ = 2mπ auf. Die
Halbwertsbreite ist dann
. Resonanzen treten bei δ = 2mπ auf. Die
Halbwertsbreite ist dann
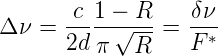 | (4.45) |
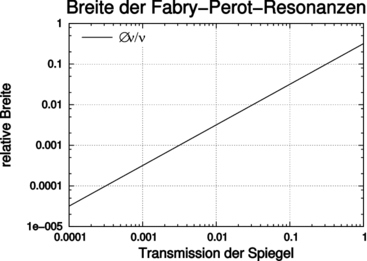
| Abbildung 4.214.: | Normierte Linienbreite als Funktion von T = 1 −R. Der Modenabstand im Fabry-Perot-Resonator ist 1. |
Hier ist F∗ = 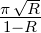 die Reflexionsfinesse. Haben die beiden
Spiegel unterschiedliche Reflektivitäten R1 und R2, so
wird für R =
die Reflexionsfinesse. Haben die beiden
Spiegel unterschiedliche Reflektivitäten R1 und R2, so
wird für R = 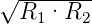 gesetzt. Die in diesem Abschnitt
berechneten Linienbreiten sind die Linienbreiten eines
passiven Resonators. Durch das aktive Medium werden
die Resonatoren entdämpft: die Linienbreiten werden
geringer.
gesetzt. Die in diesem Abschnitt
berechneten Linienbreiten sind die Linienbreiten eines
passiven Resonators. Durch das aktive Medium werden
die Resonatoren entdämpft: die Linienbreiten werden
geringer.
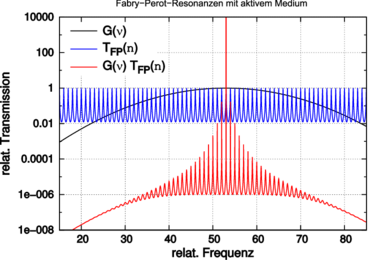
| Abbildung 4.215.: | Verstärkungsprofil (rot) eines Laserüberganges und die Resonatormoden (blau). Das kombinierte Verstärkungsprofil nach Gleichung (4.46) ist grün eingezeichnet. |
Mit einem aktiven Medium im Resonator werden diejenigen Moden verstärkt, für die die Nettoverstärkung pro pro Umlauf G(ν) = I∕I0 = exp[−2α(ν)L −γ] nach Gleichung (4.5) maximal ist. Nach Demtröder[Dem93] ist die transmittierte Intensität
![(1 − R )2G (ν)
IT = I0----------2------------2 δ
[1 − G (ν)] + 4G(ν )sin 2](phys_elektr1241x.png) | (4.46) |
In Abbildung 4.215 ist das damit berechnete Verstärkungsprofil eingezeichnet. Wenn die Verstärkung gegen 1 geht (hier mit einer Gauss-Funktion24 , die ihr Maximum bei 53 und eine Breite von 14.34 hat) geht die Gesamtverstärkung IT ∕I0 → ∞. Dieses Maximum wird bei δ = q·2π erreicht. Dabei muss anstelle der Resonatorlänge d die effektive Resonatorlänge
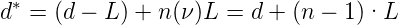 | (4.47) |
verwendet werden. L ist die Länge des Lasermediums und n(ν) der (frequenzabhängige) Brechungsindex. Die Frequenzbreite des aktiven Resonators wird
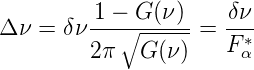 | (4.48) |
Die Finesse Fα∗ des aktiven Resonators wird unendlich, wenn die Verstärkung G(ν) → 1 wird.
Die Abbildung 4.216 zeigt, wie das Modenprofil sich in Funktion der Verstärkung ändert. Während bei niedrigen Verstärkungen die Transmission für viele Moden etwa gleich ist, beginnt eine einzelne Mode zu dominieren, wenn die Verstärkung G(ν) gegen 1 geht.
Im Gegensatz zu den der Abbildung 4.215 zugrunde liegenden Annahmen ist das Verstärkungsprofil des Lasermediums meistens sehr viel breiter als der longitudinale Modenabstand. Deshalb ist die Anzahl schwingungsfähiger Moden meistens wie in der Abbildung 4.217 gezeigt, grösser als 1. Ausnahmen sind Laserdioden wegen ihrem sehr kurzen Resonator und gewisse sehr hochgezüchtete Laseranordnungen.
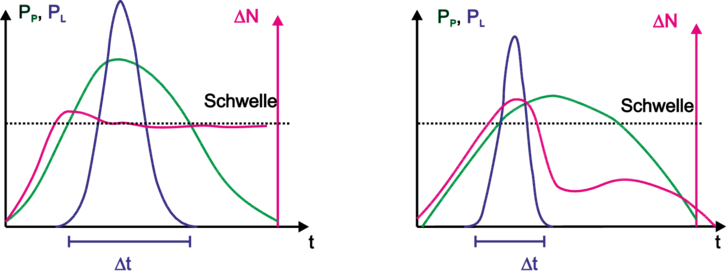
| Abbildung 4.218.: | Zeitliche Beziehung zwischen Pumppuls, Laserpuls und Besetzungsinversion. Links die Kurvenformen, wenn die Lebensdauer des unteren Laserniveaus genügend klein sind, andernfalls (rechts) wird die Pulsdauer und -energie limitiert. |
Kurze Lichtpulse könnten erzeugt werden, indem die Betriebsspannung der Lichtquelle kurzzeitig eingeschaltet wird. Die kürzesten erreichbaren Zeiten hängen von den Schaltkapazitäten und den möglichen Schaltströmen ab. Es ist schwierig, Spannungen oder Ströme kürzer als in etwa 100 ps einzuschalten.
Deshalb werden kurze Lichtpulse ausschliesslich auf optischem Wege erzeugt. Man nutzt aus, dass das Einschalten eines Lasers mit grossen Relaxationsschwingungen verbunden ist. Diese Schwingungen entstehen, weil die für eine Lasertätigkeit notwendige Inversion im Dauerbetrieb wesentlich geringer ist als im Einschaltmoment. Die die Relaxationsschwingungen beschreibenden Differentialgleichungen sind nichtlinear: der Laser ist in vielen Betriebszuständen ein chaotisches System.
Die Abbildung 4.218 zeigt den Zusammenhang der Laserleistung, der Inversion und der Pumpleistung. Wenn die Pumpe eingeschaltet wird, baut sich die Inversion parallel zum Anstieg der Pumpleistung auf. Wenn die Schwelle überschritten wird, wird die Besetzungszahl auf einem Wert, der nur unwesentlich über der Schwellinversion liegt, begrenzt. Die Laserleistung steigt rapide an und die Besetzungsinversion wird, wenn die Pumpleistung wieder abnimmt, wieder abgebaut. Der resultierende Laserpuls ist kürzer als der Pumppuls. Auf der rechten Seite der Abbildung 4.218 wird gezeigt, was passiert, wenn das untere Laserniveau nicht schnell genug entleert wird. Dann nimmt die Möglichkeit zu spontaner und induzierter Emission sehr viel schneller beschränkt. Die Besetzungszahlinversion baut sich ab, auch wenn die Pumpleistung hoch bleibt. Im Verhältnis zum Pumppuls ist der Laserpuls kürzer. Ein nächster Pumppuls kann jedoch erst dann folgen, wenn die Besetzung des unteren Laserniveaus wieder in die Nähe des Ursprungswertes abgebaut ist.
Wenn die induzierte Emission sehr stark verstärkt wird, wie zum Beispiel in Blitzlampen gepumpten Rubinlasern aber auch in Laserdioden, dann treten Relaxationsschwingungen auf. Während der Dauer des Pumppulses treten einige bis viele sogenannte Spikes, also Relaxationsschwingungen auf. Die Einhüllende der Amplitude dieser Spikes folgt der Amplitude des Pumppulses.
Ein Nachteil dieser Relaxationsschwingungen ist, dass der Zeitpunkt der einzelnen Pulse nicht gut bestimmt ist. Indem man die Verluste im Resonator gross macht, verhindert man das Anschwingen der Laserschwingung. In der Abbildung 4.220 ist gezeigt, dass, wenn man die Verluste in kurzer Zeit < 1ns erniedrigt, zu einem genau definierten Zeitpunkt ein einzelner Laserpuls entsteht.
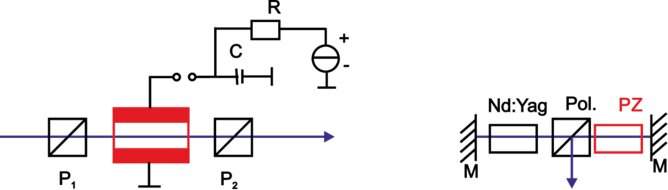
| Abbildung 4.221.: | Links die prinzipielle Schaltung einer Pockelszelle (rot), rechts eine Implementation in einem gepulsten Nd-Yag-Laser. |
Das Schalten der Verluste kann entweder über akusto-optische Schalter, elektrooptische Schalter oder durch sättigbare Absorber geschehen. Eine Implementation eines elektrooptischen Schalters ist die Pockelszelle. Die Transmission der Pockelszelle in Abb. 4.221 ist durch die Funktion
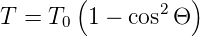 | (4.49) |
gegeben. Dabei ist Θ der Winkel der Drehung der Polarisationsebene. Dieser ist proportional zur an der Pockelszelle angelegten Spannung. Abb. 4.222 zeigt den Kurvenverlauf der Resonatorverluste, der Transmission durch die Pockelszelle in Relation zur angelegten Spannung.
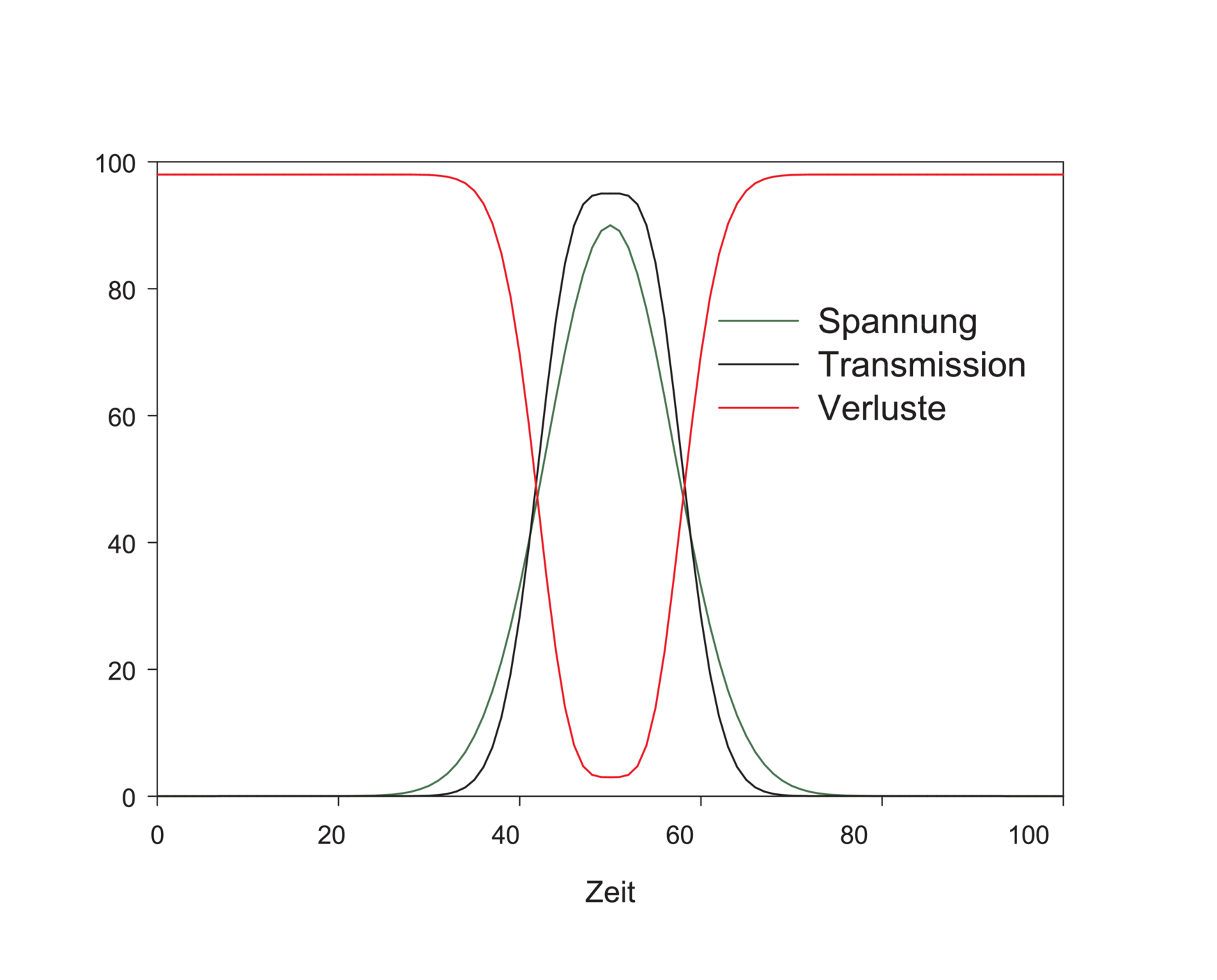
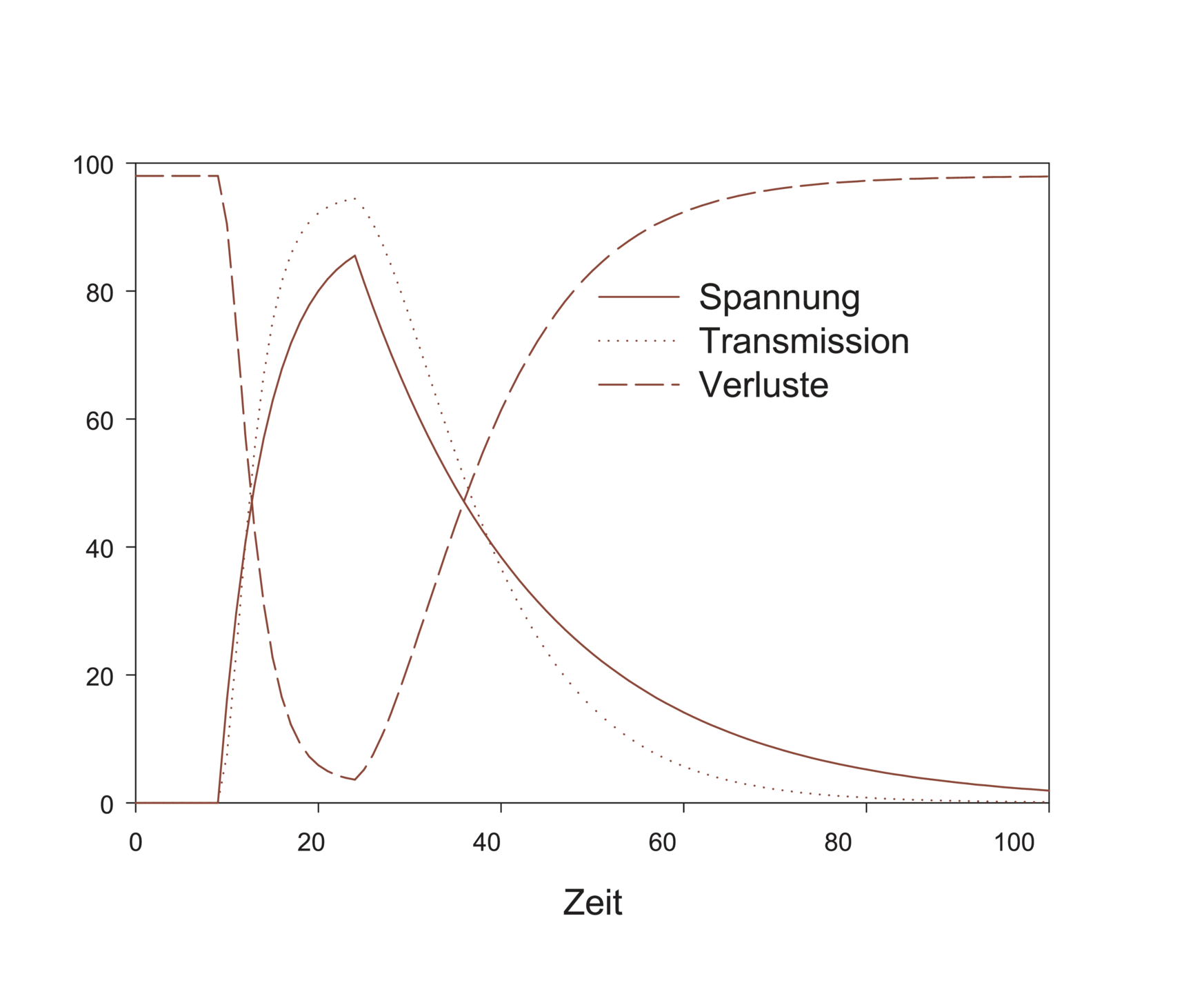
| Abbildung 4.222.: | Links sind für einen gaussförmigen Spannungspuls der Spannungsverlauf, die Transmission und die Verluste angegeben. Rechts das gleiche für einen exponentiell ansteigenden und abfallenden Puls. |
Akusto-optischer Modulator und Pulslaser mit Cavity Dumping
Im akusto-optischen Modulator wird eine Schallwelle unter schiefem Winkel zur Ausbreitungsrichtung des Lichtstrahles in einen Kristall eingestrahlt (sieh Abb. 4.224). Durch die laufende Schallwelle wird ein sich mit Schallgeschwindigkeit bewegendes moduliertes Dichteprofil erzeugt. Dieses bewirkt eine Modulation des Brechungsindexes und somit eine Bragg-Streuung am optischen Gitter.
Wir nehmen nun an, dass in diesem Kristall mit dem Brechungsindex n eine Schallwelle mit der Frequenz Ω, der Schallgeschwindigkeit cS und der Wellenlänge ΛS = cS∕Ω vorhanden ist. Wenn die Bragg-Bedingung
 | (4.50) |
erfüllt ist, dann wird der Bruchteil η der eingestrahlten Intensität in die erste Beugungsordnung abgelenkt. Hier ist λ die Wellenlänge des Lichtes. Die Beugungseffizienz η hängt von der Tiefe der Brechzahlmodulation Δn und somit von der Amplitude der Schallwelle ab. Dadurch dass das Licht durch eine laufende Schallwelle abgelenkt wird, wird seine Wellenlänge und Frequenz moduliert. Der ungebeugte Lichtstrahl hat die Frequenz ω = λ∕c, während der gebeugte Lichtstrahl um
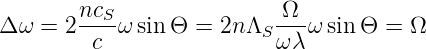 | (4.51) |
in der Frequenz Doppler-verschoben wird. Wenn die Amplitude des eingestrahlten Lichtes E0 ist, sind die Amplituden des transmittierten und gebeugten Anteils
| transmittiert | 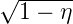 E
0 cos ωt E
0 cos ωt |
| gebeugt | 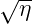 E
0 cos E
0 cos 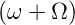 t t |
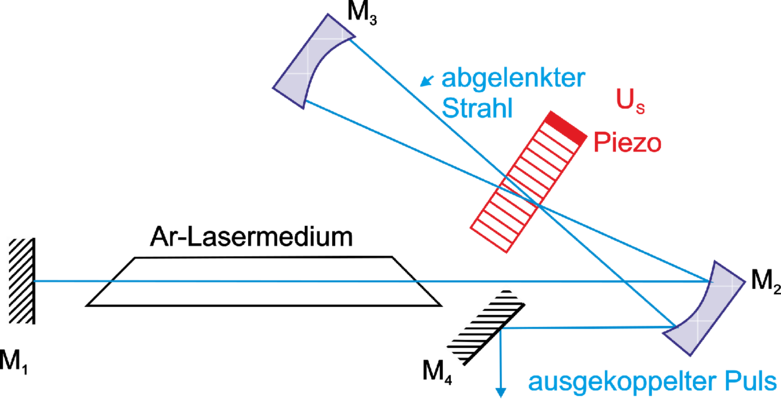
| Abbildung 4.224.: | Schematischer Aufbau der Auskopplung aus einem gütegeschalteten Laser (cavity dumping). |
Abb. 4.224 zeigt den Aufbau eines gepulsten Lasers, bei dem der akusto-optische Modulator die Auskopplung aus der Laser-Cavity steuert. Das vom Spiegel M2 herkommende Licht passiert den akusto-optischen Modulator und wird mit der Effizienz η abgelenkt. Auf dem Rückweg muss das ausgekoppelte Licht unabgelenkt durch den Modulator gehen (Effizienz 1 −η). Der Strahl, der unabgelenkt vom Spiegel M2 her kommend durch den akusto-optischen Modulator gegangen wird, wird auf dem Rückweg mit der Effizienz η abgelenkt. Im ersten Fall wird die Schallfrequenz von der Lichtfrequenz abgezählt, im zweiten Fall dazugezählt.
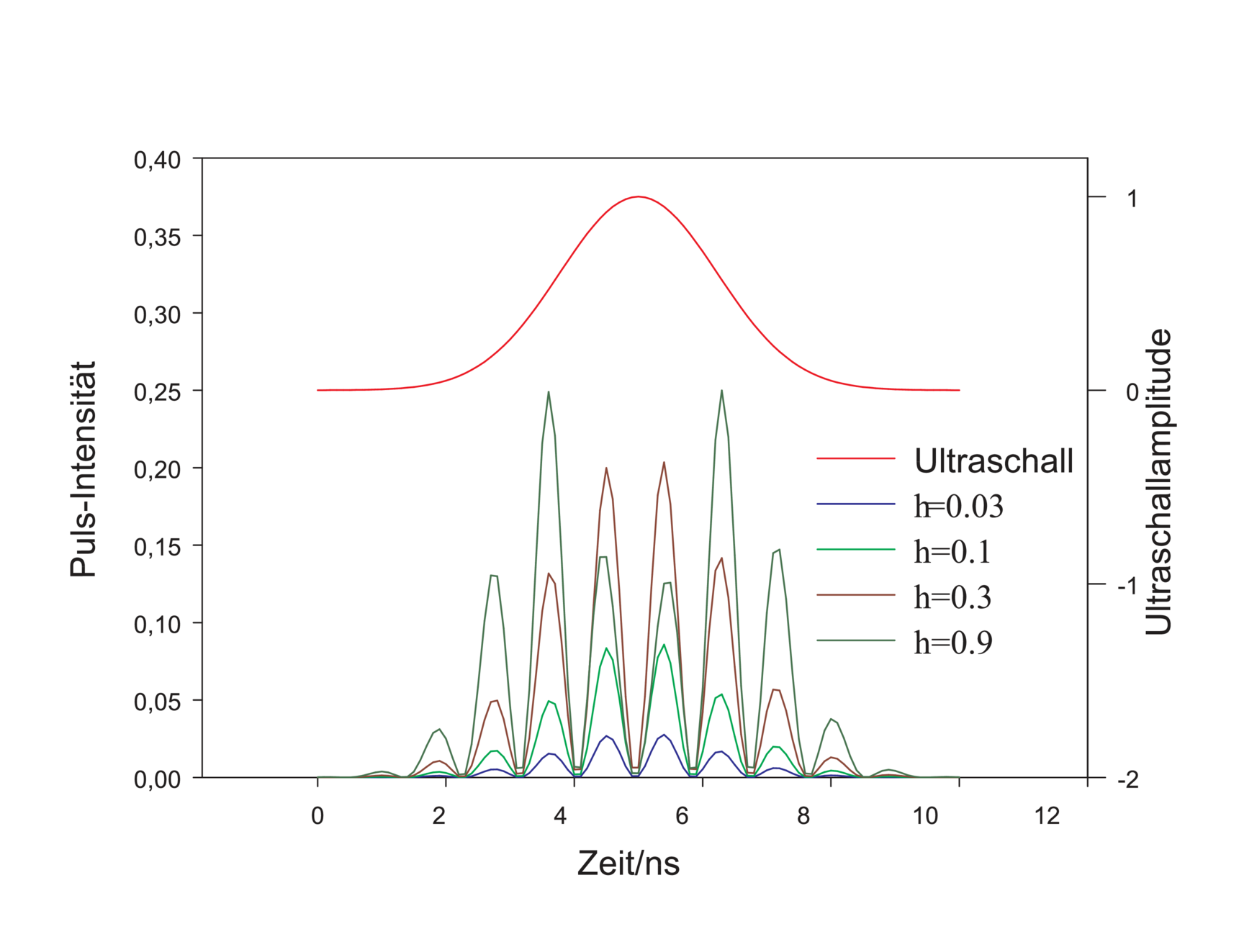
| Abbildung 4.225.: | Dargestellt ist der Verlauf des Ultraschallpulses und des Laserpulses für vier Modulationstiefen η im akusto-optischen Modulator. |
In der Auskoppelrichtung überlagern sich die Amplituden
Der ausgekoppelte Puls hat dann die Leistung
Hier ist 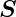 t der Poynting-Vektor und Z0 =
t der Poynting-Vektor und Z0 = 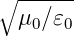 der Wellenwiderstand des Vakuums. Während der zeit
des Ultraschallimpulsdes wird η(t)
der Wellenwiderstand des Vakuums. Während der zeit
des Ultraschallimpulsdes wird η(t)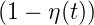 der in
der Laserkavität eingeschlossenen optischen Leistung
ausgekoppelt. Abb. 4.225 zeigt die Ultraschallamplitude und
für vier verschiedene Beugungseffizienzen η den zeitlichen
Verlauf des ausgekoppelten Pulses. Interessant ist, dass für
η = 0.5 ein Maximum erreicht wird. Bei der in Abb. 4.225
gezeigten Kurve für η = 0.9 resultieren deshalb zwei
Intensitätsmaxima.
der in
der Laserkavität eingeschlossenen optischen Leistung
ausgekoppelt. Abb. 4.225 zeigt die Ultraschallamplitude und
für vier verschiedene Beugungseffizienzen η den zeitlichen
Verlauf des ausgekoppelten Pulses. Interessant ist, dass für
η = 0.5 ein Maximum erreicht wird. Bei der in Abb. 4.225
gezeigten Kurve für η = 0.9 resultieren deshalb zwei
Intensitätsmaxima.
Mit dem Verfahren des Cavity-Dumping erreicht man bei Ionenlasern oder bei Farbstofflasern Pulslängen von 10 − 100ns mit Pulsfolgefrequenzen zwischen null und 4 MHz.
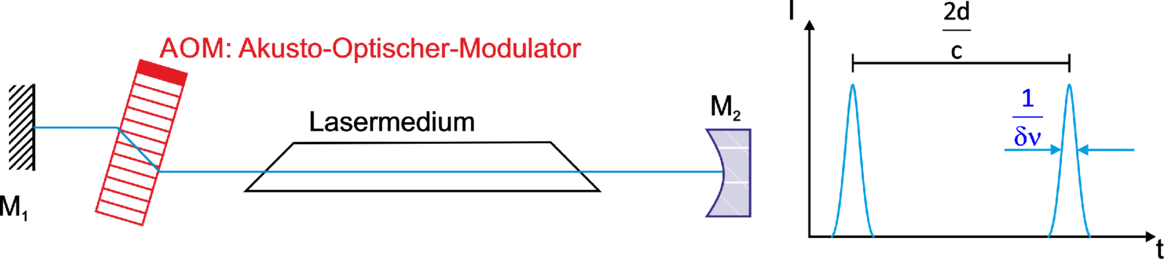
| Abbildung 4.226.: | Mit einem akusto-optischen Modulator im Ultraschallbereich kann eine aktive Modenkopplung erreicht werden. Die Lasermoden in einem |
Wenn, wie in Abbildung 4.226 gezeigt, ein akusto-optischer Modulator in den Laserresonator eingefügt wird, dann entstehen im Frequenzspektrum Nebenfrequenzen. Ist die Modulationsfrequenz f, dann existieren neben der Grundfrequenz des Lasers ν auch die Frequenzen ν ±f. Wenn die Modulationsfrequenz gleich dem Modenabstand im Resonator ist, das heisst wenn f = c∕2d ist, dann können die Seitenbänder auch an der Laseroszillation teilnehmen. Diese Seitenbänder werden auch moduliert, so dass alle vom Verstärkungsprofil des Lasermediums her möglichen Moden anschwingen.
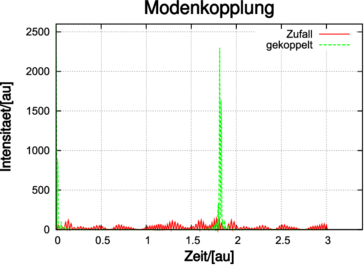
| Abbildung 4.227.: | Dargestellt einerseits die Überlagerung von 51 Moden mit zufälliger Phase und gleicher Amplitude sowie die Überlagerung von 51 modengelockter Moden. Die resultierende Pulsüberhöhung ist augenfällig. |
Durch die Modulation schwingen die Lasermoden nicht unabhängig, da ihre Phasen durch den Modulator gekoppelt sind. Abb. 4.227 zeigt, die resultierende Ausgangsamplitude für viele Lasermoden mit zufälligen Phasen sowie für gekoppelte Phasen. Die Intensität bei gekoppelten Phasen wird periodisch sehr gross. Andererseits zeigt das Ausgangssignal bei zufälligen Phasen das auch von Laserdioden her bekannten vergrösserte Rauschen.
Der akusto-optische Modulator moduliert die Transmission des Laserresonators mit
![[ ( ) ]
T = T [1 − δ(1 − cos Ωt)] = T 1 − 2δ sin2 Ωt-
0 0 2](phys_elektr1255x.png) | (4.54) |
Unter der Annahme, dass alle Lasermoden die gleiche Amplitude Ak,0 = A0 haben wird bei einem kleinen Modulationsgrad δ ≤ 1∕2 die instantane Amplitude der k-ten Mode zu
![Ak(t) = TA0 cos ωkt = T0A0 [1 − δ(1 − cosΩt )]cosωkt](phys_elektr1256x.png) | (4.55) |
Wenn nun die Modulationsfrequenz gleich der Umlaufzeit des Lichtes im resonator ist, also wenn Ω = 2πc∕(2d) so wird die k + 1-te Mode
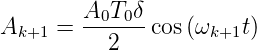 | (4.56) |
Diese Modulation wird, sofern sie innerhalb der Verstärkungsbandbreite des Lasermediums liegt, verstärkt. Die k + 1-te Mode wird nun wieder moduliert, genauso wie alle nachfolgenden Moden. Das gleiche gilt auch für Moden mit abnehmenden Indizes. Durch die Modulation sind alle Phasen der verschiedenen Moden periodisch gleich. Dies tritt in der Gleichung (4.55) immer zu den Zeiten
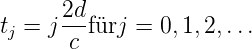 | (4.57) |
Ist die Bandbreite der verstärkbaren Moden (oberhalb der Laserschwelle) δν und Δν der Abstand der einzelnen Moden, dann ist die Anzahl der verstärkten Moden
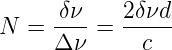 | (4.58) |
Die Überlagerung von 2m + 1 = N Lasermoden mit gleicher Amplitude führt zur Gesamtamplitude
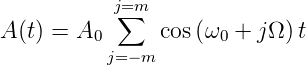 | (4.59) |
Die Laserintensität I(t) = A2(t) wird dann
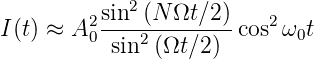 | (4.60) |
Wie auch aus Abbildung 4.227 ersichtlich ist, bekommt man eine Pulsfolgezeit T und eine Pulsbreite Δt.
Damit wird klar, dass die kürzest mögliche Pulsdauer von der Breite des Verstärkungsprofils abhängt. Lasermedien mit schmalen Linien wie zum Beispiel Gaslaser sind für Modenkopplung ungeeignet. Die Spitzenleistung eines modengekoppelten Lasers geht wie N2, das heisst auch wieder mit der spektralen Bandbreite des Lasers. Die Eignung von Lasermedien zur Erzeugung kurzer Pulse wird in Tabelle 4.11 zusammengefasst.
| Lasermedium | Wellenlänge | Frequenzbreite δν | Pulsbreite ΔT |
| HeNe | 633 nm | 1.5 GHz | 500 ps |
| Argon-Ionenlaser | 488 nm, 514 nm | 5-7 GHz | 150 ps |
| Nd-Glas-Laser | 1064 nm | 200 GHz | 5 ps |
| Farbstoff-
oder
Farbzentrenlaser | 600 nm | 30 THz | 30 fs |
| Tabelle 4.11.: | Demtröder [Dem93] gibt die oben zusammengefassten Möglichkeiten zur Erzeugung kurzer Pulse an. |
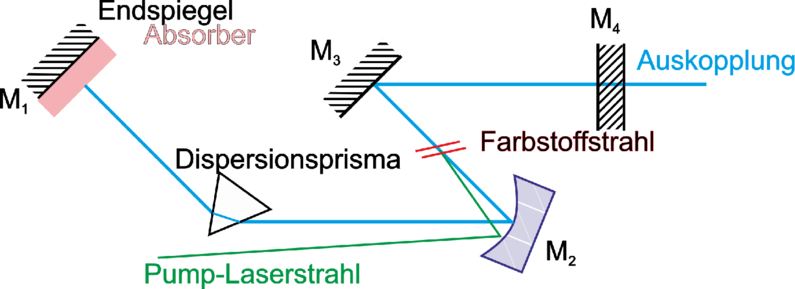
| Abbildung 4.228.: | Die Modenkopplung wird bei diesem Aufbau durch einen sättigbaren Absorber erreicht. |
Passive Modenkopplung Schneller als ein optischer Modulator schalten sättigbare Absorber. Wichtig ist, dass die Absorptionsniveaus des Absorbers eine möglichst kurze Abklingzeit haben. Abb. 4.228 zeigt den Aufbau eines Lasers mit einem sättigbaren Absorber. Dieser wird vor einem der Resonatorspiegel montiert, so dass nur an einem wohldefinierten Ort die Absorption sich ändern kann. Durch die Absorption im Medium werden die Verluste vergrössert. Die Verstärkung im Lasermedium muss so gross sein, dass das gesamte System die Schwellenverstärkung erreicht. Das Lasermedium emittiert vor dem Erreichen der Schwelle spontan und dann induziert verstärkt und in statistischen Abständen. Die Amplitude schwankt stark. Wenn einer dieser Pulse die Schwellenenergie erreicht, dann wird durch die Verstärkung die Absorption im sättigbaren Absorber leicht verringert. Dieser erste Puls löst also eine Photonenlawine aus, die einerseits die Verstärkung des Pulses erhöht und andererseits verhindert, dass die anderen Schwankungen weiter verstärkt werden. Da das Absorptionsmedium eine sehr kurze Lebensdauer hat, ist es schon kurz nach dem Puls wieder in seinem hoch absorbierenden Zustand. Dieser umlaufende Puls ist der einzige, der verstärkt wird.
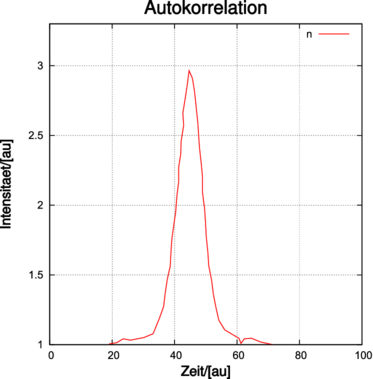
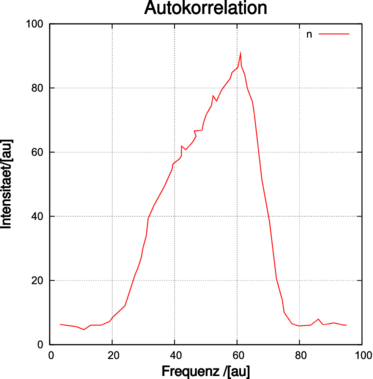
| Abbildung 4.229.: | Links wird die Autokorrelation, rechts das Spektrum eines modengekoppelten Pulses gezeigt (nach Demtröder [Dem93]). Die Pulslänge ist 0.5 ps, die spektrale Breite 1nm. |
Die Pulsform und damit, über die Fouriertransformation auch das Spektrum, hängen von den Verstärkungseigenschaften des Mediums und von den spektralen Absorptionseigenschaften des Absorbers. Abbildung 4.229 zeigt links ein Beispiel für die Pulsform und rechts das Spektrum dieses Pulses. Die in Abb. 4.229 gezeigte Pulsbreite von 0.5ps ist die kürzeste, mit passiver Modenkopplung erreichbare Pulslänge.
Bei synchron gepumpten Lasern wird die Pumpleistung in einem Takt mit ganzahligem Verhältnis zur Umlaufszeit der Pulse im Resonator gepumpt. Die Abbildung 4.230 zeigt auf der linken Seite einen möglichen Aufbau eines synchron gepumpten Lasersystems[Dem93]. Der Argon-Ionenlaser wird im Laserresonator mit einem akusto-optischen Modulator moduliert. Die Pumpleistung trifft mit der Umlauffrequenz der Pulse im Farbstofflaser auf das Lasermedium, einen Farbstoffstrahl. Von allen möglichen, durch spontane Emission entstandenen Photonen werden nur diejenigen verstärkt, die synchron mit der Pumpleistung im Resonator umlaufen.
Die rechte Seite von Abbildung 4.230 den Verlauf der Verstärkung (oben) und die Intensitäten von Pumppuls und Laserpuls. Die Verstärkung würde bei sehr grossen Verlusten der gestrichelten Kurve folgen. Durch die Emission des Laserpulses, und da das synchrone Pumpen ähnlich wie ein Absorber im Resonator des Farbstofflasers wirkt, wird die Besetzungszahlinversion stark abgebaut. nur ein einzelner, aber sehr kurzer Laserpuls entsteht.
Die Umlaufszeit der Pulse im Laserresonator ist T = 2d∕c bei einem Resonator mit der Länge d. Typischerweise kann man mit einem synchron gepumpten Lasersystem Pulslängen von 0.5ps erreichen. Wenn der Resonator eine Länge von 1m hat, ist die Pulsfolgefrequenz 150MHz. Ein Fehler von 1μm der Länge des Resonators führt zu einer Verbreiterung der Pulse auf 1ps.
Durch einen akusto-optischen Modulator im Resonator des Pulslasers können die Verluste für alle ausser jeden k-ten Puls so erhöht werden, dass sie nicht anschwingen. Durch dieses Verfahren, das auch Cavity Dumping genannt wird, kann die Pulsfolgefrequenz erniedrigt werden. damit ist es möglich, auch längere Relaxationen auszumessen.
Sehr kurze Laserpulse erhält man mit sogenannten CPM-Lasersystemen. Eine mögliche Anordnung eines solchen Lasersystems ist in der Abbildung 4.231 gezeigt. Die Idee hinter dieser Anordnung ist die folgende:
Indem man die Dicke des Absorberstrahls sehr dünn (< 100μm) wählt, ist die Laufzeit durch das Medium kleiner als etwa 400fs. Da nur die Überlagerung beider Pulse den Absorber auf niedrige Absorption schalten kann, ist dies nur bei einer perfekten Überlagerung der beiden Pulse, also wenn die Zeitunsicherheit sehr viel kleiner als 400fs ist, möglich.
Um die kürzesten möglichen Pulse zu erhalten, ist es notwendig, die Dispersion der Spiegel und der sonstigen optischen Elemente zu kompensieren[Dem93]. Durch die CPM-Technik konnten Pulse mit einer Länge von unter 100fs erzeugt werden. Durch sättigbare Braggspiegel und eine Dispersionskompensation mindestens bis zur 3. Ordnung sind Pulse die kürzer als 10fs sind, möglich.
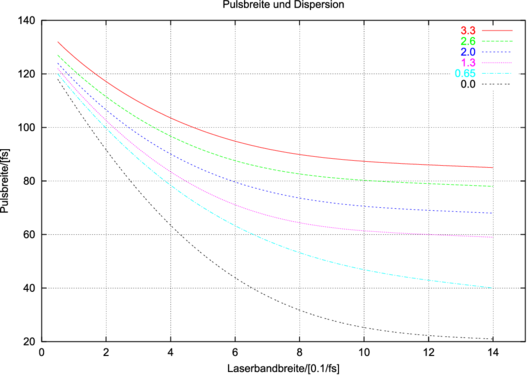
| Abbildung 4.232.: | Abhängigkeit der Pulsbreite von der Bandbreite eines Lasermediums unter Berücksichtigung der Dispersion. |
Wir nehmen an, dass ein optischer Puls mit der spektralen Energieverteilung E(ω) und der spektralen Breite δω den zeitlichen Intensitätsverlauf
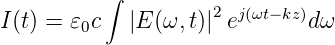 | (4.63) |
hat. Dieser Puls läuft durch ein Medium mit dem Brechungsindex n(ω). Seine Form ändert sich, da die Gruppenlaufzeit für die verschiedenen spektralen Anteile verschieden lang ist. Wenn vph die Phasengeschwindigkeit ist, bekommt man
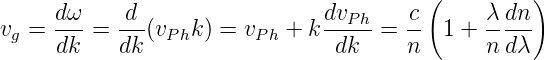 | (4.64) |
Diese Gruppengeschwindigkeit vg hat die Dispersion
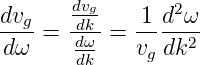 | (4.65) |
Bei Pulsen mit sehr hoher Intensität hängt der Brechungsindex von der Pulsleistung ab, ist also n(ω,I) = n0(ω) + n1I(t). Damit hängt die Phase auch von der Intensität ab.
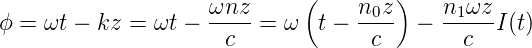 | (4.66) |
Damit hängt aber auch die Frequenz eines Pulses von seiner instantanen Intensität ab. Mit A = n1ωz∕c bekommt man
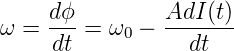 | (4.67) |
Aus Gleichung (4.31) ersieht man, dass während des Intensitätsanstiegs eines Pulses seine Frequenz ω abnimmt. Zum Pulsende hin nimmt die Frequenz wieder zu. Durch diese Selbst-Phasenmodulation wird die spektrale Breite eines Pulses nach dem Durchgang durch ein dispersives Medium grösser.
Da der Brechungsindex n bei normaler Dispersion dn0∕dλ < 0 die roten Anteile schneller propagieren lässt als die blauen Anteile, läuft der Puls auseinander. Das heisst wegen n0 wird der Puls zeitlich breiter, wegen n1 wird der Puls auch spektral breiter.
Unter der Annahme dass sich die Amplitude entlang der Ausbreitungsrichtung nur langsam ändert (λ∂2E∕∂z2 «∂E∕∂z) wird die Wellengleichung
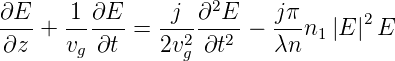 | (4.68) |
Ein Puls der Länge τ der mit der Geschwindigkeit vg durch ein Medium der Länge L läuft, wird auf
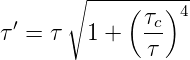 | (4.69) |
verbreitert. dabei ist τc die kritische Pulsbreite
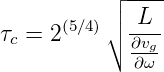 | (4.70) |
Je kürzer der Puls ist, desto schneller läuft er auseinander. Zwei Beugungsgitter im Abstand D können die unterschiedlichen Laufzeiten der roten und blauen Anteile wieder kompensieren und so den Puls wieder komprimieren. Der optische Weg (siehe Abb. 4.233) ist dann
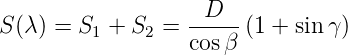 | (4.71) |
dabei ist γ = π−(α+β). Nun verwenden wir das Additionstheorem für den Kosinus cos(α + β) = cos α cos β − sin α sin β wird Gleichung (4.71)
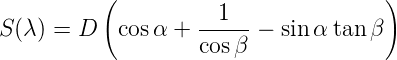 | (4.72) |
Die Dispersion eines Gitters ist dβ∕dλ = 1∕(d cos β) wobei d die die Gitterkonstante ist. Damit wird die Weglängendispersion
![dS- dS-dβ- ----------D-λ-----------
dλ = dβ dλ = [ ( λ)2 ]3∕2
d2 1 − sinα − d )](phys_elektr1273x.png) | (4.73) |
Nach Gleichung (4.73) nimmt der optische Weg mit zunehmender Wellenlänge zu. Damit lässt sich die normale Dispersion in Medien kompensieren. Ohne diese Dispersionskompensation, die unter Einbeziehung von Fasern und Prismen auch Effekte zweiter und dritter Ordnung kompensieren kann, wären fs-Laser nicht denkbar.
Ein besonders eleganter Aufbau eines Kurzpuls-Lasersystems verwendet sättigbare Bragg-Spiegel[SHK00] als sättigbares Medium. Konventionelle sättigbare Absorber haben eine Bandbreite und eine Mittenfrequenz, die vom Material abhängt. Andererseits ist bekannt, dass die Breite der Bandlücke bei Halbleitermaterialien durch die Einstellung des Mischungsverhältnisses bei ternären und quaternären Materialien in weiten Grenzen einstellbar ist. Durch die Verwendung von Schichtstrukturen können so hochwertige optische Schichten mit einstellbarer Bandbreite und einstellbarer Frequenz erzeugt werden.
Wenn die optische Intensität bei der Beleuchtung eines Halbleitermaterials eine materialabhängige Schwelle überschreitet, befindet sich ein Grossteil der Elektronen des Valenzbandes in einem angeregten Zustand im Leitungsband. Das Material wird also transparent und ändert damit auch seinen Brechungsindex. Wenn nun ein Multischichtsystem so erzeugt wird, dass es bei hohen Intensitäten eine Reflektivität in der Nähe von 1 hat, dann kann dies wie ein sättigbarer absorber wirken.
Das in der Abbildung 4.234 gezeigte Lasersystem[Kel95] verwendet einen sättigbaren Bragg-Spiegel, markiert mit AFPSA (antiresonant Fabri-Perot saturable absorber). Der Kurzpulslaser wird durch zwei Laserdionen über jeweils eine Strahlformungsoptik gepumpt. Als aktives Medium wird ein Cr:LiSAF-Kristall verwendet. Die Auskopplungseite des Laserresonators beinhaltet zwei Prismen zur Dispersionskompensation. Das andere Ende des Resonators wird durch einen sättigbaren Bragg-Spiegel gebildet. Die Schichtfolge in diesem Spiegel ist im Einsatz links angegeben.
Die schematische Kennlinie eines sättigbaren Bragg-Spiegel in der Abbildung 4.235 zeigt, dass die Reflektivität mit steigender Intensität zunimmt. Damit hat, wie bei den sättigbaren Absorbern der intensivste aller beim Einschalten anschwingenden Pulse die grösste Verstärkung. Nur dieser Puls wird im weiteren Verlauf durch den Laser verstärkt.
Ein sättigbarer Bragg-Spiegel aus AlxGa1−xAs∕AlAs limitiert die Pulsweite auf 34 fs[SHK00]. Der in der Abbildung 4.234 gezeigte AFPSA sättigbare Bragg-Spiegel ermöglicht durch eine geschicktere Ausnutzung der Materialien eine Erhöhung der Bandbreite und damit eine Pulslänge von 19 fs. Durch eine Kombination der Materialien Al0.8Ga0.2As und CaF2 sind Bandbreiten von 500nm um eine Mittenfrequenz von 800nm möglich[SHK00]. Damit können mit einem Laser analog zur Abbildung 4.234 Pulse mit einer Länge von weniger als 10fs erzeugt werden.
 Lizenzinformationen
Lizenzinformationen