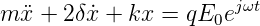

In diesem Abschnitt sollen einige grundlegende optische Messverfahren diskutiert werden. Der Abschnitt erhebt keinen Anspruch auf Vollständigkeit. Der interessierte Leser wird auf Werke wie das von Perez[Pér96a] oder Demtröder[Dem93] verwiesen.
Absorption und Dispersion hängen in einem klassischen Modell[Dem93] eng zusammen. Man beschreibt das optische Medium als eine Sammlung von getriebenen harmonischer Oszillatoren der Form
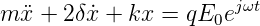 | (4.1) |
Wie üblich ist m die Masse eines oszillierenden Teilchens, k die Federkonstante, q die Ladung auf der Masse, δ der Dämpfungsterm. Setzt man nun γ = 2δ∕m und ω02 = k∕m und setzt als Lösung x = x0 exp jωt an, so bekommt man
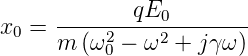 | (4.2) |
Durch die erzwungene Schwingung der Ladung q entsteht ein induziertes elektrisches Dipolmoment
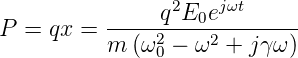 | (4.3) |
Bei N Oszillatoren pro Volumen ist die induzierte elektrische Polarisation P pro Volumeneinheit durch
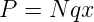 | (4.4) |
gegeben. Die Polarisation ist jedoch in der Elektrodynamik auch mit der induzierenden elektrischen Feldstärke E durch
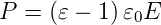 | (4.5) |
verknüpft. Die relative Dielektrizitätszahl 𝜀 hängt mit der Brechzahl n über
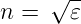 | (4.6) |
zusammen. Durch Kombination von (4.3) bis (4.6) erhält man
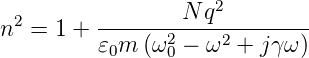 | (4.7) |
Die Brechzahl n(ω) ist komplex und kann deshalb als
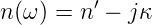 | (4.8) |
geschrieben werden. Beachtet man, dass die Lichtgeschwindigkeit
c im Medium von der Brechzahl n abhängt (c = c0∕n)
und setzt dies in die Gleichung einer ebenen Welle
E = E0 exp ![[j (ωt − Kz )]](phys_elektr1282x.png) ein und berücksichtigt, dass
Km = nK0 ist, so bekommt man
ein und berücksichtigt, dass
Km = nK0 ist, so bekommt man
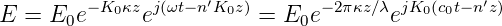 | (4.9) |
Eine elektromagnetische Welle wird in einem Medium entsprechend dem Gesetz
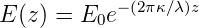 | (4.10) |
abgeschwächt. Der Imaginärteil des Brechungsindexes ist für die Absorption zuständig. Bei Gasen ist n nur unwesentlich grösser als 1. Es gilt dann in guter Näherung, dass n2 − 1 ≃ 2(n − 1) ist. betrachten wir den Real- und den Imaginärteil in der Nähe einer Resonanzfrequenz, ist also |ω −ω0|«ω0 so erhält man[Dem93]
In der Literatur wird das Absorptionsgesetz üblicherweise mit Intensitäten formuliert. Die Lichtintensität wird beim Durchgang durch ein Medium wie
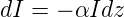 | (4.13) |
abgeschwächt. Aus dieser Gleichung folgt das Beer-Lambert’sche Absorptionsgesetz
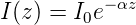 | (4.14) |
Die aus einem klassischen Modell für eine Atom abgeleitete Absorption kann in den Beer-Lambert’schen Absorptionskoeffizienten durch quadrieren umgerechnet werden (die Intensität ist proportional zum Quadrat der Amplitude).
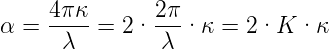 | (4.15) |
Die Abbildung 4.236 zeigt einen Aufbau zur Messung der Absorption. Das Licht aus einer Quelle, entweder polychrom oder monochrom und eventuell durchstimmbar, wird durch das zu untersuchende Medium der Länge L geschickt. Die Länge des Mediums muss so bemessen werden, dass der Detektor 1 in einem Bereich betrieben wird, in dem sein Signal-zu-Rausch-Verhältnis noch genügend ist. Bei Proben mit einem grossen α muss die Länge klein sein, bei Proben mit einer kleinen Absorption wie bei Gasen ist eine grosse Wirkungslänge notwendig.
Da die Lichtquellen nicht immer stabil arbeiten, oder da sie, wenn sie in der Frequenz durchgestimmt werden, ihre Intensität ändern, ist es oftmals notwendig, den in Abbildung 4.236 angegebenen Referenzzweig zu verwenden. Das Signal des Detektors 1 wird durch das Signal des Detektors 2 geteilt. Da die Kennlinie der verwendeten Detektoren nichtlinear sein kann, sollten beide mit etwa der gleichen Lichtintensität betrieben werden.
Bei einem empfindlichen Messaufbau können langsame Schwankungen des Umgebungslichtes wie auch nicht zu kontrollierende Streulichtquellen stören. Wie im Abschnitt 2.8 über Rauschen gezeigt, sind Messungen über lange Zeiten besonders vom 1∕f-Rauschen betroffen. Deshalb wird bei den meisten optischen Messungen das Licht mit einer Frequenz von etwa 1kHz moduliert. Oft wird dies wie in der Abbildung 4.237 gezeigt, ein Chopperrad verwendet. Mit einer Lichtschranke wird die Taktfreqenz gemessen und als Referenz in die den Detektoren nachgeschalteten Lock-In-Verstärker eingespiesen. Damit lassen sich die meisten Störquellen genügend stark unterdrücken.
Eine Reflektivitätsmessung (Abbildung 4.238) ist ähnlich aufgebaut wie eine Absorptionsmessung. Das Licht aus einer wird in einen Referenzstrahl und einen Teststrahl aufgeteilt. Beide werden mit einem Chopper-Rad getaktet. Das reflektierte Licht wird gesammelt und auf einen Detektor gebracht. Die Reflexion kann spekular oder diffus sein.
Eine mögliche Anwendung von Reflexionsmessungen ist die Bestimmung von Schadstoffen in der Luft. Eine andere mögliche Anwendung ist die Messung der induzierten Transparenz oder der induzierten Brechzahländerung in Halbleiterproben. Dabei müssen jedoch sehr kleine Unterschiede der Reflektivität in der Gegenwart eines grossen Untergrundes bestimmt werden.
Auch der Aufbau für Polarisationsmessungen (Abbildung 4.239 ist sehr ähnlich dem Aufbau zur Messung der Absorption. Das Licht aus einer wird in einen Referenzstrahl und einen Teststrahl aufgeteilt. Beide werden mit einem Chopper-Rad getaktet. Der Polarisationszustand des Teststrahls wird in einem Polarisator vor der Probe festgelegt. nach der Transmission der Probe wird der Polarisationszustand mit einem Analysator ausgemessen. Der restliche Aufbau ist analog zu weiter oben diskutierten Versuchsaufbauten.
Die Messanordnung nach Abbildung 4.239 kann zum beispiel benutzt werden, um den Kerr-Effekt oder die Chiralität von Molekülen auszumessen.
Spektrometer dienen zur Messung der Wellenlängenabhängigkeit der Intensität von Licht. Dieses Licht kann entweder direkt von einer Quelle abgeleitet sein, oder aber das Resultat eines optischen Experimentes sein.
Ein gebräuchliches Spektrometer wenn die spektrale Auflösung nicht allzu hoch sein soll, ist das Prismenspektrometer analog zur Abbildung 4.240. Nach Perez[Pér96a] kann die Dispersion von Glas durch
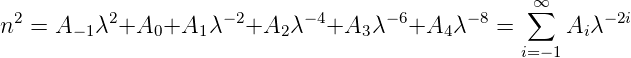 | (4.16) |
beschrieben werden. Für eine bestimmte Glassorte sind die Parameter
Die Dispersion eines Materials dn∕dλ kann aus der Gleichung (4.16)berechnet werden. Wir setzen f = n2 und erhalten
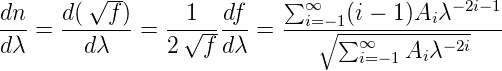 | (4.18) |
Bezeichnet man mit δ den Winkel zwischen dem einfallenden Strahl vor dem Prisma und dem das Prisma verlassenden Strahl, so kann man die Winkeldispersion
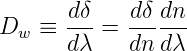 | (4.19) |
Der zweite Term hängt nur vom Material ab, der erste Term beschreibt die Geometrie. Nach Perez[Pér96a] gilt für Prismen
Da α und Θ konstant sind, gilt auch
Daraus folgt
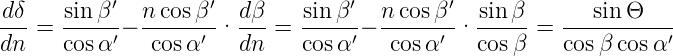 | (4.22) |
Im Minimum der Ablenkung hat eine Änderung des Einfallswinkels nur einen kleinen Einfluss auf die Ablenkung. Der Ausgangswinkel hängt wie
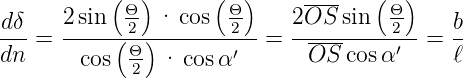 | (4.23) |
von den Eingangsgrössen ab. Die Winkeldispersion ist also
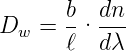 | (4.24) |
Wenn man das Spektrum in der Brennebene einer Linse mit einem Schirm oder einer CCD-Kamera beobachtet, benötigt man die Lineardispersion
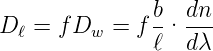 | (4.25) |
Das Auflösungsvermögen eines Prismenspektrographen ist über
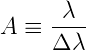 | (4.26) |
definiert. Wenn die optischen Elemente von genügender Qualität sind, dann hängt das Auflösungsvermögen des Spektrometers von der Beugung des Lichtes am Eintrittsspalt ab. Bei einem (auch fiktiven) Spalt der Breite B ist die Halbwertsbreite des Beugungsmusters nach Rayleigh
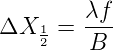 | (4.27) |
Damit wird
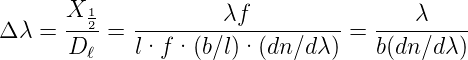 | (4.28) |
Somit ist das Auflösungsvermögen eines Prismenspektrometers durch
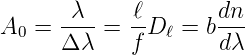 | (4.29) |
Wenn man das Bild des Spaltes vor der Lichtebene in der Detektionsebene vergrössert, dann wird
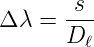 | (4.30) |
über die Grösse des Bildes s festgelegt. Damit ist das Auflösungsvermögen
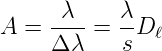 | (4.31) |
Das Prismenspektrometer ist optimal eingestellt[Pér96a], wenn
gilt. Typischerweise kann man ein Auflösungsvermögen (bei voll ausgeleuchtetem Prisma!) von A = 2000 erreichen.
In einem Gitterspektrometer wird ein Beugungsgitter als dispersives Element verwendet. Abbildung 4.241 zeigt einen typischen Aufbau eines solchen Spektrometers. Licht tritt durch einen Eintrittsspalt ein und wird durch den Hohlspiegel M1 in paralleles Licht umgewandelt. Wie bei einer Linse wird der Öffnungswinkel durch eine Numerische Apertur charakterisiert. Das parallele Licht wird durch das Gitter G in seine spektralen Anteile zerlegt. Eine bestimmte Richtung wird durch den Hohlspiegel M2 auf den Austrittsspalt fokussiert. Hinter diesem befindet sich der Detektor. Alternativ kann anstelle der Kombination aus Spalt und Detektor ein ein- oder zweidimensionaler Detektor verwendet werden. Dies kann eine Diodenzeile, eine CCD-Zeile oder ein flächenhafter CCD-Detektor sein.
Um eine optimale Empfindlichkeit zu erreichen müssen die folgenden Voraussetzungen erfüllt sein:
Die Beugungserscheinungen an einem Gitter können
mit einer Vektorgleichung beschrieben werden. Ist 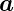 der
Gittervektor des Gitters und ist
der
Gittervektor des Gitters und ist 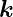 0 der Wellenvektor des
einfallenden Lichtes und
0 der Wellenvektor des
einfallenden Lichtes und 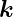 der Wellenvektor des gestreuten
Lichtes, so gilt mit der Vereinbarung
der Wellenvektor des gestreuten
Lichtes, so gilt mit der Vereinbarung 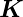 =
= 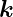 −
−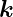 0
0
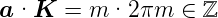 | (4.33) |
Diese Gleichung kann auch mit Winkeln formuliert werden. Sei Θ0 der Winkel des einfallenden Lichtes zur Senkrechten auf das Gitter und sei Θ der entsprechende Winkel des gebeugten Lichtes und sei α ≡ Θ0 −π, dann ist
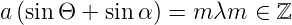 | (4.34) |
Das Gitter soll nun N Spalte haben. Wir setzen u = 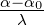 ,
wobei α = sin Θ und α0 = sin Θ0 die Richtungskosinusse der
gebeugten und der einfallenden Welle sind[Pér96b]. Die
Spaltbreite eines einzelnen Spaltes sei 𝜖. Dann ist die
gestreute Intensität hinter dem Gitter
,
wobei α = sin Θ und α0 = sin Θ0 die Richtungskosinusse der
gebeugten und der einfallenden Welle sind[Pér96b]. Die
Spaltbreite eines einzelnen Spaltes sei 𝜖. Dann ist die
gestreute Intensität hinter dem Gitter
![[sin(πu𝜖)]2 [ sin(N πua )]2
I(u) = N 2𝜖2 --------- · -----------
πu 𝜖 N sin (πua )](phys_elektr1315x.png) | (4.35) |
Wenn das Gitter nicht voll ausgeleuchtet wird, muss für N die Anzahl beleuchteter Gitterstriche eingesetzt werden.
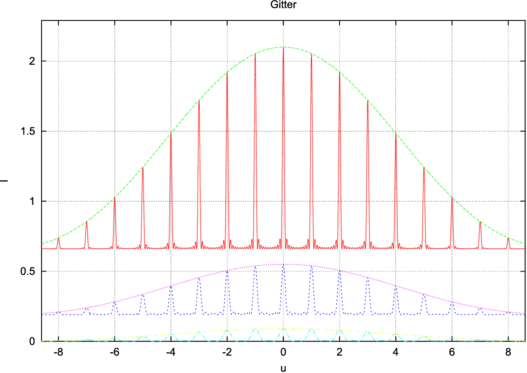
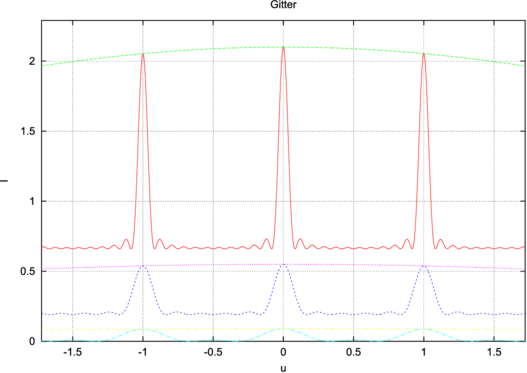
| Abbildung 4.242.: | Intensität des gebeugten Lichtes als Funktion der Anzahl beleuchteter Spalte. Links ist eine Übersicht, rechts die Detailansicht. Von unten nach oben sind N = 3,6 und 12 beleuchtete Spalte dargestellt. Die sonstigen Gitterparameter sind a = 1 und 𝜖 = 0.1 |
Abbildung 4.242 zeigt den Intensitätsverlauf in Abhängigkeit der Anzahl beleuchteter Gitterstriche N. Aus (4.35) ist ersichtlich, dass die Intensität wie N2 sich verhält. Wenn also ein Gitter in einem Gitterspektrometer nicht richtig ausgeleuchtet ist, verliert man sehr schnell sehr viel an Intensität auf dem Detektor.
Die Höhe der Beugungsmaxima ist durch
![[ ]2
2 2 sin(πu-𝜖)-
Im (u) = N 𝜖 πu𝜖](phys_elektr1316x.png) | (4.36) |
gegeben. Weiter kann man berechnen, dass die Breite eines Maximums proportional zur beleuchteten Breite L = N·a ist.
Die Winkeldispersion eines Gitters wird aus (4.34) berechnet:
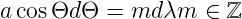 | (4.37) |
Im Gegensatz zu einem Prisma werden längere Wellenlängen stärker gebeugt. Die Winkeldispersion ist
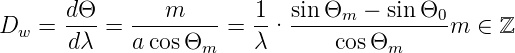 | (4.38) |
Für höhere Ordnungen ist die Winkeldispersion also grösser. Analog zum Prisma kann auch bei einem Gitter eine lineare Dispersion definiert werden.
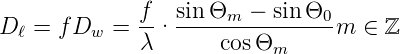 | (4.39) |
Auch beim Gitter gibt es einen Einfallswinkel, bei dem die Ablenkung minimal ist. Der Ablenkwinkel ist δ ≡ Θ − Θ0. Daraus folgt, dass
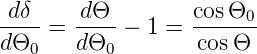 | (4.40) |
sein muss. Man sieht, dass entweder Θ = Θ0 oder Θ = −Θ0 sein muss, um einen Extremwert von δ zu erhalten. Der erste Fall entspricht dem nicht gebeugten Strahl und ist nicht von Interesse. Eine Analyse der zweiten Ableitung zeigt, dass dort die Ablenkung des Strahls ein Minimum hat.
Das Auflösungsvermögen eines Gitters[Pér96a] ist
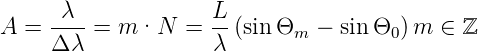 | (4.41) |
Zum Beispiel hat ein Gitter mit einer Breite von 2cm und 500Linien∕mm bekommt man A = 20000. Das Auflösungsvermögen hat ein Maximum. In (4.41) können die beiden Sinus dem Betrage nach maximal 1 werden. Also gilt
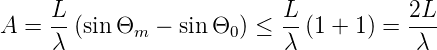 | (4.42) |
Für das vorhin diskutierte Gitter ist also A ≤ 80000 bei einer Wellenlänge von λ = 0.5μm. Da bei höheren Ordnungen m die maximale Intensität schnell abnimmt, wird man ein Gitter im allgemeinen mit einer Ordnung in der Nähe von eins betreiben.
Ein Gitterspektrometer hat bei gleicher Grösse von Gitter oder Prisma etwa eine zehn mal bessere Auflösung.
Wenn eine sehr hohe spektrale Auflösung gefordert ist, verwendet man häufig Fabri-Perot-Spektrometer. Bei diesen Spektrometern wird, wie in der Abbildung 4.243 gezeigt, Licht in einen optischen Resonator eingekoppelt. Da das licht teilweise mit sich selber interferiert, können nur Eigenmoden des Resonators oder Frequenzen in deren Nähe durch den Resonator propagieren. Wenn R die für beide Spiegel gleiche Reflektivität ist, und M = 4R∕(1 −R2)ist, dann wird die transmittierte Intensität
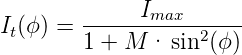 | (4.43) |
ϕ ist dabei die Phasenveschiebung beim Umlauf um den Resonator.
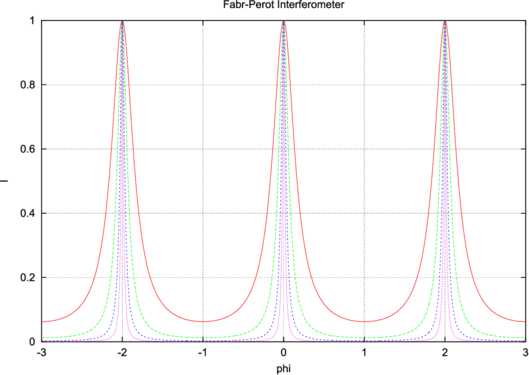
| Abbildung 4.244.: | Kennlinie eines Fabri-Perot-Inerferometers für Reflektivitäten von 0.6, 0.8, 0.9 und 0.95 beziehungsweise Werte von M von 15, 80, 360 und 1520 (von oben) |
Abbildung 4.244 zeigt den Intensitätsverlauf als Funktion der Phase ϕ für M = [15, 80, 360, 1520].
Wir betrachten nun einen Lichtstrahl, der unter dem Winkel α zur Achse des Fabri-Perot-Interferometers auf das Interferometer trifft. Wenn weiter der Abstand der beiden planparallelen Spiegel L sei, ist die Phasendifferenz im Brennpunkt der Linse durch
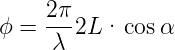 | (4.44) |
gegeben. Die Phasendispersion (das Äquivalente zur Winkeldispersion) wird dann
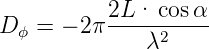 | (4.45) |
Wenn man annimmt, dass Δϕ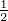 die minimal messbare
Phasendifferenz bei der Halbwertsbreite der Transmissionsfunktion
ist, dann ist die minimal auflösbare Wellenlängendifferenz
Δλ = Δϕ
die minimal messbare
Phasendifferenz bei der Halbwertsbreite der Transmissionsfunktion
ist, dann ist die minimal auflösbare Wellenlängendifferenz
Δλ = Δϕ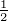 ∕|Dϕ|. Damit ist das Auflösungsvermögen
durch
∕|Dϕ|. Damit ist das Auflösungsvermögen
durch
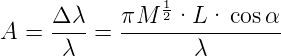 | (4.46) |
gegeben. Mit den Definitionen
wird das Auflösungsvermögen
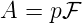 | (4.48) |
Die Grösse F heisst Finesse. p ist die Interferenzordnung. Die Tabelle 4.12 zeigt eine Zusammenstellung der erreichbaren Auflösung. Diese ist für nicht allzu gute Spiegel etwa 100 bis 1000 mal besser als Gitterspektrometer und etwa 1000 bis 10000 mal besser als Prismenspektrometer.
| R | 0.60 | 0.80 | 0.90 | 0.95 | 0.99 |
| M | 15 | 80 | 360 | 1520 | 39600 |
| F | 6 | 14 | 30 | 61 | 313 |
| A | 0.24 × 106 | 0.56 × 106 | 1.2 × 106 | 2.45 × 106 | 125 × 106 |
| Δλ(pm) | 2 | 0.89 | 0.42 | 0.21 | 0.004 |
| Tabelle 4.12.: | Auflösungsvermögen, kleinste auflösbare Wellenlängenänderung und Finesse eines Fabri-Perot-Interferometers[Pér96a]. Die konstanten Werte sind λ = 0.5μm, L = 1cm und α ≈ 0. daraus folgt p = 40000. |
Die Messung ultrakurzer Pulse sowie die Messung von Vorgängen, die kürzer als etwa eine ps sind, sind mit rein elektrischen Verfahren nicht möglich. Die beste Zeitauflösung erreichen optische Verfahren und elektrooptische Verfahren.
Ein optischer Korrelator, wie er in Abb. 4.245 gezeigt besteht aus einem Strahlteiler, in dem der ankommende Puls geteilt wird, einer Verzögerungsleitung, die einen Puls zeitlich verzögert wird, sowie einem nichtlinearen Medium, in dem die beiden Pulse überlagert werden. Der einkommende Puls soll die Intensität I(t) = c𝜀0E2(t) und die Halbwertsbreite ΔT. Dieser Puls wird in zwei Teilpulse I1(t) und I2(t) aufgeteilt. Dabei durchlaufen die beiden Pulse unterschiedliche Wege S1 und S2. Der Wegunterschied ΔS = S2 −S1 ist äquivalent zu einem Zeitunterschied τ = ΔS∕c. Nach der Überlagerung der beiden Pulse ist die Intensität
Ein linearer Detektor mit einer Integrationszeit T würde das Signal
Für Zeiten T, die gross gegen die Pulsdauer ΔT sind, kann das Integral über alle Zeiten erweitert werden. Als Resultat wird die Korrelationsfunktion erster Ordnung G(1) erhalten.
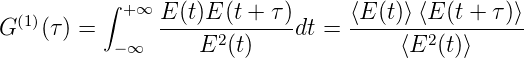 | (4.51) |
messen. An den Grenzen hat die Korrelationsfunktion G(1) die Werte G(1)(0) = 1 und G(1)(∞) = 0. Bei monochromatischem Licht würde die Funktion G(1)(τ) mit der Periode T = λ∕(2c) oszillieren. Da jedoch kurze Pulse nicht monochromatisch sind, verschmiert sich die Korrelation. Ein langsamer Detektor, dessen Zeitkonstante viel grösser als die Pulsdauer ist, misst ein konstantes Signal. Dies muss so sein, da das Ausgangssignal des Detektors proportional zur eingestrahlten Energie und nicht proportional zur eingestrahlten Leistung ist.
Um eine zeitliche Auflösung zu bekommen, ist es notwendig, einen nichtlinearen Detektor zu verwenden. Eine Komponente der Übertragungsfunktion[Dem93] könnte
![I (2ω, t,τ ) = A [I1(t) + I2(t + τ)]2](phys_elektr1334x.png) | (4.52) |
sein. Die Konstante A gibt die Stärke der Nichtlinearität an. Das Signal bei der Frequenz 2ω ist
![A- ∫ [⟨ 2⟩ ⟨ 2⟩ ]
S(2ω, t) = T · I(2ω, t,τ)dt = A I1 + I2 + 4⟨I1(t)·I2(t + τ)⟩](phys_elektr1335x.png) | (4.53) |
Die ersten beiden Terme sind von τ unabhängig. Sie ergeben ein konstantes Untergrundssignal. Der letzte Term enthält die Information über die Pulsform. Nach Demtröder rührt der Faktor 4 von der Addition der Wahrscheinlichkeiten der Photonen 1 und 2 und umgekehrt her. Die Korrelationsfunktion 2. Ordnung ist
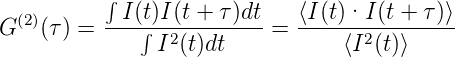 | (4.54) |
Wenn I1 = I2 = 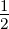 I ist, wird das detektierte Signal
I ist, wird das detektierte Signal
![[ ] [ ]
S (2ω,τ ) = A G (2)(0) + 2G (2)(τ) = A 1 + 2G (2)(τ)](phys_elektr1338x.png) | (4.55) |
Für eine Zeitverzögerung von τ = 0 wird das Signal S(2ω,τ) = 3A maximal. Wenn die Zeitverzögerung sehr gross wird, geht der term G(2) → 0, und das Ausgangssignal wird konstant S(2ω,τ) = A, aber nicht null.
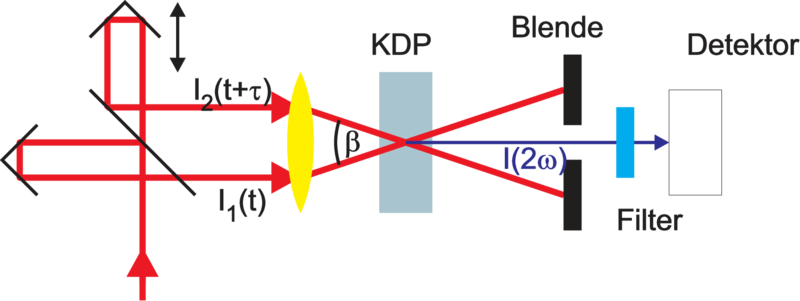
| Abbildung 4.246.: | Untergrundfreier Korrelator. Die Nichtlinearität in einem Material wie KDP (Kaliumdihydrogenphosphat) dient zur Korrelation. |
Die Messanordnung in der Abbildung 4.246 ermöglicht eine
untergrundsfreie Messung. Um in einem Verdopplerkristall ein
Signal bei der Frequenz 2ω zu erzeugen, muss sowohl der
Ort der beiden Impulse übereinstimmen wie auch der
resultierende 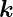 -Vektor. In der Abbildung 4.246 ist die
Orientierung des Kristalls so gewählt, dass zwei Photonen
aus dem gleichen Teilstrahl kein frequenzverdoppeltes
Photon erzeugen können, da ihre
-Vektor. In der Abbildung 4.246 ist die
Orientierung des Kristalls so gewählt, dass zwei Photonen
aus dem gleichen Teilstrahl kein frequenzverdoppeltes
Photon erzeugen können, da ihre 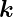 -Vektoren nicht mit der
Gitterorientierung kompatibel sind[Dem93]. Nur wenn
zwei Photonen aus je aus einem der beiden Teilstrahlen
sich überlagern, stimmt die Impulsbedingung und ein
frequenzverdoppeltes Photon kann entstehen.
-Vektoren nicht mit der
Gitterorientierung kompatibel sind[Dem93]. Nur wenn
zwei Photonen aus je aus einem der beiden Teilstrahlen
sich überlagern, stimmt die Impulsbedingung und ein
frequenzverdoppeltes Photon kann entstehen.
Die Frequenzverdoppelung ist nicht der einzige nichtlinear-optische Effekt der zur Erzeugung einer Korrelation zweiter Ordnung benützt werden kann. Die Abbildung 4.247 zeigt schematisch einen Aufbau zur Zwei-Photonen-Absorption in einer Flüssigkeit. Wieder ist die Wahrscheinlichkeit, eine Absorption bei der halben Wellenlänge des eingestrahlten Lichtes zu erhalten proportional zum Quadrat der Intensität.
Da in dem gezeigten Versuchsaufbau zwei gegenläufige Pulse sich überlagern, entsteht ein räumliches Interferenzmuster. Absorption bei der halben Wellenlänge und die daraus folgende Emission von Fluireszenzlicht ist auf den räumlichen Bereich der Überlappung beider Pulse beschränkt. Da ddiese pulse senkrecht zu ihrer Ausbreitungsrichtung ausgedehnt sind, ist es nicht möglich, eine Wechselwirkungszone, die kleiner als 0.3 mm ist, abzubilden. daher ist die zeitliche Auflösung der Messmethode für kurze Pulse nach Abbildung 4.246 auf Pulse mit einer Länge grösser als 1 ps beschränkt.
| Pulsform | Gleichung | 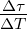 | ΔT·Δν |
| Rechteck | I(t) = 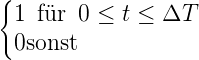 | 1 | 0.886 |
| Gauss-Profil | exp 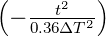 | 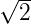 | 0.441 |
| Hyperbolisches
Sekansprofil | sech2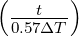 | 1.55 | 0.315 |
| Tabelle 4.13.: | Breiten von Autokorrelationsfunktion und Laserpuls nach Demtröder[Dem93] |
Die Gleichung (4.54) zeigt, dass G(2) symmetrisch in τ ist. deshalb lässt sich aus der Autokorrelationsfunktion keine aussage über die Pulsform machen. Auch zur Abschätzung der Pulsdauer muss eine Modellannahme über das Pulsprofil gemacht werden. Die Tabelle 4.13 zeigt, wie die ’gemessene’ Pulsdauer von der profilform abhängt. Um die Pulsform zu bestimmen müssten Korrelationen höherer Ordnung (wie die Frequenzverdreifachung) gemessen werden.
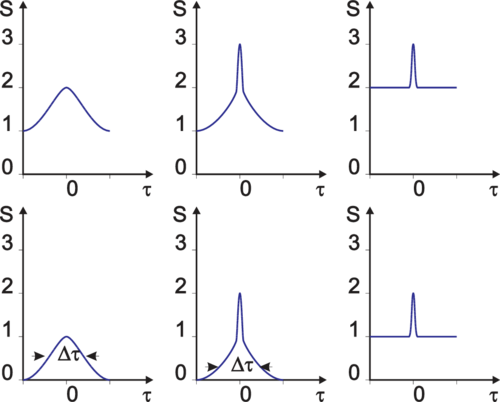
| Abbildung 4.248.: | Autokorrelationsprofile. Gezeigt werden a) ein Fourier-limitierter Puls, b) ein Rauschpuls, c) kontinuierliches Rauschen. Die obere Reihe zeigt das Messresultat bei einer Messung mit Untergrund, die untere bei einer untergrundfreien Messung |
Abbildung 4.248 zeigt schliesslich, dass auch weisses Rauschen (Siehe Abschnitt 2.8) ein Autokorrelationssignal erzeugt. Um Pulse eindeutig nachzuweisen muss die Funktion 1 + G(2)(τ) möglichst genau gemessen werden.
 Lizenzinformationen
Lizenzinformationen