Vierpole und Vierpoltheorie

[Nächste Seite] [Vorherige Seite] [vorheriges Seitenende] [Seitenende] [Ebene nach oben] [PDF-Datei][Epub-Datei][Andere Skripte]

2.5 Vierpole und Vierpoltheorie

Ein Vierpol ist ein elektrisches Schaltteil (einfach oder zusammengesetzt), das von aussen mit vier Klemmen angesteuert wird[Ros83]. Zwei der Klemmen dienen als Eingang, zwei als Ausgang. Wenn nun am Eingang eine Spannung angelegt wird, so ﬂiest ein Strom, der aber auch von der Belastung am Ausgang abhängt. Genauso kann der Ausgang auf den Eingang rückwirken. Ebenso gibt es Kopplungen vom Eingang auf den Ausgang.

Die Vierpoltheorie beschreibt in einer linearen Näherung um den Arbeitspunkt die Wirkung einer Schaltung. Im Gegensatz zu der Anwendung von Blockschaltbildern wird hier die gegenseitige Beeinﬂussung von Schaltungen berücksichtigt.

pict

Abbildung 2.35.:

Anschlüsse, Ströme und Spannungen bei einem Vierpol

Die Ströme an den Klemmen 1 und 1’ sowie 2 und 2’ sind jeweils gleich. Für lineare, zeitinvariante passive Vierpole gibt es sechs Möglichkeiten, die gegenseitigen Beeinﬂussungen in einem Gleichungssystem zu beschreiben. So könnte man zum Beispiel schreiben:

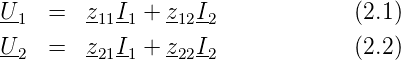
U1 = z11I1 + z12I2 (2.1) U2 = z21I1 + z22I2 (2.2)

Die z_ij sind komplexwertige Koeﬃzienten, die wie folgt deﬁniert sind:

| z11 = ∂∂UI1|| Leerlaufeingangsimpedanz (2.3) -1 I2=0 ∂U1|| negativer z12 = ∂I2|I=0 R¨uckwirkungswiderstand (2.4) | 1 z = ∂U2|| Kernwiderstand (2.5) -21 ∂I1 I2=0 vorw¨arts | z22 = ∂U2|| negative (2.6) ∂I2 I1=0 Leerlaufausgangsimpedanz

Die obigen Gleichungen geben auch die Messvorschrift für diese Impedanzen wieder. Um z₁₁ zu bestimmen, speist man bei oﬀenem Ausgang den Strom I₁ ein und misst die resultierende Spannung U₁. Die Gleichungen können kompakt als Matrix geschrieben werden, eine Tatsache die die Rechenarbeit sehr erleichtert.

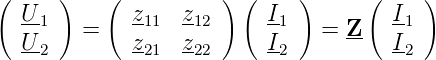( ) ( ) ( ) ( ) U-1 z11 z12 I1 I1 U- = z- z- I- = Z- I- 2 21 22 2 2

(2.7)

Die Matrix Z heisst die Widerstandsmatrix. Durch Permutation können die anderen möglichen Darstellungen erhalten werden. Üblich sind:

Widerstandsmatrix

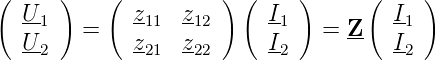( ) ( ) ( ) ( ) U-1 z11 z12 I1 I1 U- = z- z- I- = Z- I- 2 21 22 2 2

(2.8)

Leitwertform

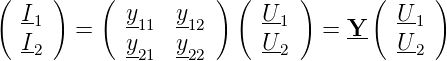( ) ( ) ( ) ( ) I1 y11 y12 U-1 U-1 I2 = y y U-2 = Y- U-2 -21 -22

(2.9)

Kettenform

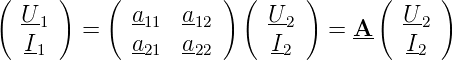( ) ( ) ( ) ( ) U-1 a11 a12 U2 U-2 I = a a I = A- I -1 -21 -22 -2 -2

(2.10)

Hybridform (Reihen-Parallel-Form)

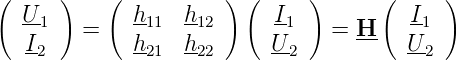( ) ( ) ( ) ( ) U-1 h11 h12 I1 I1 I2 = h21 h22 U2 = H-- U2

(2.11)

Die Matrix H ist besonders beliebt zur Angabe der Vierpolparameter von Transistoren. Bei Transistoren , inherent nichtlinearen Bauteilen, werden die Vierpolparameter am Arbeitspunkt angegeben, es sind also diﬀerentielle Parameter. Auch gebräuchlich für Transistoren ist die Y-Matrix. Die Vierpolparameter können wie in Tabelle 2.13 angegeben ineinander umgerechnet werden.

a₁₁	a₁₂
a₂₁	a₂₂

	−
	−

−
−

−
−

	−
	−

z₁₁	z₁₂
z₂₁	z₂₂

	−
−


−

	−
	−

	−
−

y₁₁	y₁₂
y₂₁	y₂₂

	−


	−


−

	−

h₁₁	h₁₂
h₂₁	h₂₂

Δa

a₁₁a₂₂ −a₁₂a₂₁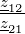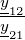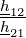

−

−

Δz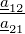

−

z₁₁z₂₂ −z₁₂z₂₁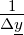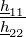

−

Δy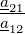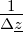

−

y₁₁y₂₂ −y₁₂y₂₁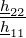

Δh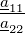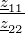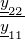

−

h₁₁h₂₂ −h₁₂h₂₁

Tabelle 2.13.:

Umrechnung der Vierpolparameter

2.5.1 Zusammenschaltung von Vierpolen

Die Vierpoltheorie erlaubt, das Zusammenschalten einzelner Bauelemente unter Berücksichtigung von Eingangs- und Ausgangswiderständen einfach zu berechnen. Kabel und Leitungen können mit Ketten von Vierpolen modelliert werden.

pict

Abbildung 2.36.:

Serienschaltung zweier Vierpole

Die Serienschaltung in Abbildung 2.36 kann mit folgenden Bedingungsgleichungen berechnet werden:

U-11 + U-21 = U-1 U- + U- = U- 12 ′22 2 I11 = I-21 = I1 I12 = I′22 = I2 (2.12)

Aus Gleichungen (2.8) und (2.12) kann die Matrix-Form der Serieschaltung berechnet werden:

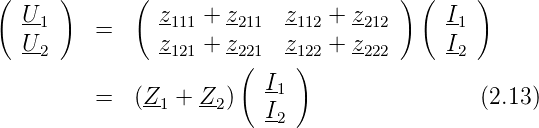
( ) ( ) ( ) U-1 = z111 + z211 z112 + z212 I1 U-2 z121 + z221 z122 + z222 I2 ( ) = (Z- + Z- ) I1 (2.13) 1 2 I2

Die Notation z_abc bedeutet, dass das Element z_bc aus der Matrix Z_a gemeint ist. Die Matrizen der einzelnen Vierpole addieren sich also bei einer Serienschaltung.

pict

Abbildung 2.37.:

Parallelschaltung zweier Vierpole

Bei der Parallelschaltung ﬁndet man analog:

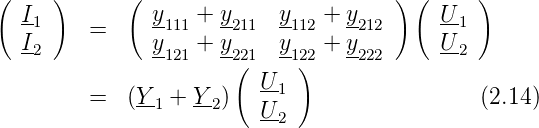
( ) ( ) ( ) I- y + y y + y U- 1 = -111 -211 -112 -212 1 I2 y121 + y22(1 y12)2 + y222 U-2 U-1 = (Y-1 + Y-2) U- (2.14) 2

Man kann sich die Regeln für die Parallelschaltung von Vierpolen einfach merken: Wie bei Widerständen addieren sich bei einer Parallelschaltung die Leitwerte.

pict

Abbildung 2.38.:

Kettenschaltung zweier Vierpole

Bei der Kettenschaltung gilt:

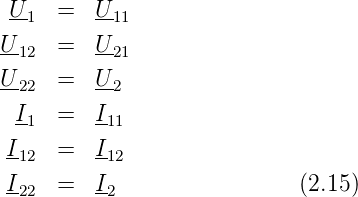
U = U -1 -11 U12 = U21 U- = U- 22 2 I1 = I11 I- = I- 12 12 I22 = I2 (2.15)

Unter Verwendung der Gleichungen (2.10)für die Kettenform erhält man

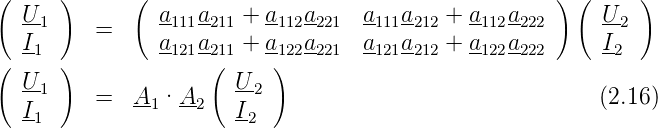
( ) ( ) ( ) U- a- a- + a- a- a- a- + a- a- U- 1 = 111 211 112 221 111 212 112 222 2 ( I1 ) a121a2(11 + a)122a221 a121a212 + a122a222 I2 U-1 U-2 I- = A1 ·A2 I- (2.16) 1 2

Wie bei jeder Matrixmultiplikation ist die Kettenschaltung von der Reihenfolge abhängig. Physikalisch kann man sich das wie folgt klar machen: Der Eingang des zweiten Vierpols belastet den Ausgang des ersten, während sein Ausgang unbelastet ist. Ebenso wir der Eingang des ersten von einer idealen Quelle angesteuert. Wechselt man nun die Reihenfolge, so sind die jeweiligen Ein- und Ausgänge nicht mehr gleich belastet. Entsprechend muss aus physikalischer Sicht das Resultat von der Reihenfolge der Vierpole abhängen.

2.5.2 Übertragungsfunktion eines Vierpols

Vielfach möchte man die Spannungs- oder Stromverstärkung eines mit der Lastimpedanz Z_L belasteten Vierpols wissen (Abbildung 2.39 . Die Lastimpedanz kann komplex sein, wir behandeln so auch die Frage nach kapazitiv belasteten Ausgängen.

pict

Abbildung 2.39.:

Übertragungsfunktion eines Vierpols

Ausgangsstrom I₂ und Ausgangsspannung U₂ hängen dann wie folgt zusammen:

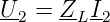U2 = ZLI2-

(2.17)

Mit der Kettengleichung (2.10)wird

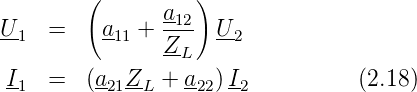
( ) U = a + a12 U --1 -11 ZL -2 I1 = (a21ZL + a22)I2 (2.18)

Damit ergibt sich für die Übertragungsfunktion der Spannung

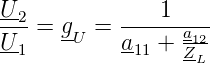U-2= g = ---1-a--- U-1 -U a11 + Z12 L

(2.19)

und des Stromes

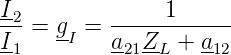I2- -----1------ I = gI = a Z + a -1 -21L -12

(2.20)

Der Leistungsübertragungsfaktor ist

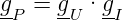g = g ·g -P -U I-

(2.21)

Die Eingangsimpedanz ist

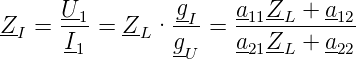U1- -gI a11ZL--+-a12 ZI = I = ZL· g = a Z + a -1 -U -21-L -22

(2.22)

Weiter sind die Übertragungsimpedanz

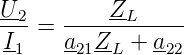U-2 = -----ZL----- I1 a21ZL + a22

(2.23)

und die Übertragungsadmittanz

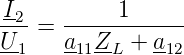I2- -----1------ U = a Z + a --1 -11-L -12

(2.24)

Die Eingangsimpedanz Z_I hängt nach Gleichung (2.22) von der Ausgangsimpedanz Z_L ab. Sie kann Werte zwischen

ZI |Z =∞ = a11 Leerlaufeingangsimpedanz (2.25) -L aa21 ZI |ZL=0 = a1222 Kurzschlusseingangsimpedanz(2.26)

Analog erhält man für die Ausgangsimpedanz Z_A abhängig von der Quellimpedanz Z_Q

Z- | = a22- Leerlaufausgangsimpedanz (2.27) A ZQ=∞ a21 ZA |Z- =0 = a1a2- Kurzschlussausgangsimpedanz(2.28) Q 11

Der Wellenwiderstand des Eingangs Z₀₁ oder Ausgangs Z₀₂ ist das geometrische Mittel aus den entsprechenden Kurzschluss- und Leerlauﬁmpedanzen.

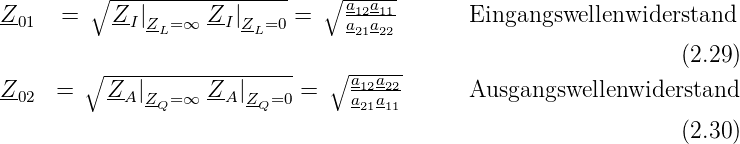
∘ ------------------ ∘ ------ Z01 = ZI| ZI| = a12a11 Eingangswellenwiderstand ZL=∞ ZL=0 a21a22 ∘ ------ (2.29) Z- = ∘ Z--|------Z--|-----= a12a22 Ausgangswellenwiderstand 02 A ZQ=∞ A ZQ=0 a21a11 (2.30)

Der Wellenwiderstand ist gerade der Abschlusswiderstand, für den der Vierpol angepasst ist. Ein mit Z₀₂ am Ausgang abgeschlossener Vierpol hat gerade die Eingangsimpedanz Z₀₁. Im Anpassungsfall, d.h. wenn die Impedanz der Quelle Z_Q = Z₀₁ ist und wenn der Lastwiderstand Z_L = Z₀₂ ist, hat man Leistungsanpassung

Die Wellenwiderstände lassen sich durch die Messung von Kurzschluss- und Leerlauﬁmpedanzen bestimmen. Diese Eigenschaft wird verwendet, um mit Netzwerkanalysatoren komplexe Hochfrequenzleiter oder Bauelemente auszumessen.

Besonders einfach ist die Bestimmung der Wellenwiderstände bei symmetrischen Vierpolen mit a₁₁ = a₂₂. Dann ist

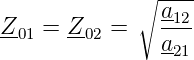∘ ---- Z01 = Z02 = a12 a21

(2.31)

2.5.3 Ersatzstrukturen für Vierpole

Für passive Vierpole (δa = a₁₁a₂₂ −a₁₂a₂₁ = 1) können die Kettenparameter a_ij durch die Ein- und Ausgangsimpedanzen bestimmt werden (Messrezept).

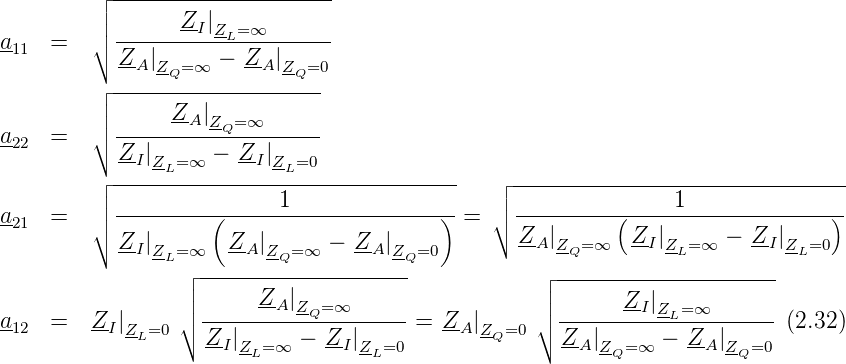
┌ --------------------- ││ Z | a- = │∘ -------I-ZL=-∞------- 11 ZA |Z-=∞ − ZA |Z-=0 ┌ -----Q-----------Q-- ││ Z- | a- = │∘ -------A-ZQ=-∞------ 22 ZI |Z- =∞ − ZI|Z-=0 ┌ -----L----------L---------------- ┌ -------------------------------- ││ ----------------1---------------- ││ ---------------1---------------- a21 = │∘ ( ) = ∘ ( ) ZI |ZL= ∞ ZA |ZQ= ∞ − ZA |ZQ=0 ZA |ZQ= ∞ ZI |ZL= ∞ − ZI|ZL=0 ┌│ -------------------- ┌ --------------------- ││ ZA |Z- =∞ ││ ZI |Z =∞ a12 = ZI|Z-=0 ∘ ----------Q---------= ZA |Z-=0 │∘ -----------L--------- (2.32) L ZI |ZL=∞ − ZI |ZL=0 Q ZA |ZQ= ∞ − ZA |ZQ=0

Das Übertragungsverhalten eines Vierpols lässt sich nun mit Ersatzschaltungen modellieren.

pict

Abbildung 2.40.:

Ersatzschaltung eines Vierpols: T- Glied (Sternschaltung)

Man erhält zum Beispiel für die Sternschaltung in Abbildung 2.40 folgende Beziehungen

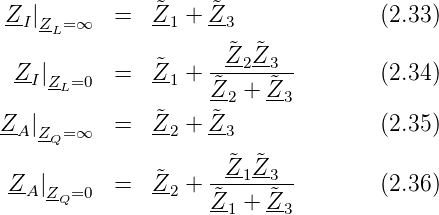
Z- | = Z˜ + ˜Z- (2.33) I ZL=∞ 1 3 -Z˜2-˜Z3-- ZI |ZL=0 = Z˜1 + ˜ ˜ (2.34) Z2 + Z3 ZA |ZQ=∞ = Z˜2 + ˜Z3 (2.35) ˜ ˜ Z | = Z˜ + -Z1-Z3-- (2.36) -A ZQ=0 -2 ˜Z1 + Z˜3

Weitere mögliche Ersatzschaltbilder sind in den Abbildungen 2.41 und 2.42 dargestellt.

pict

Abbildung 2.41.:

Ersatzschaltung eines Vierpols: π- Glied (Dreiecksschaltung)

pict

Abbildung 2.42.:

Ersatzschaltung eines Vierpols: Kreuzglied

[Nächste Seite] [Vorherige Seite] [vorheriges Seitenende] [Seitenanfang] [Ebene nach oben]
©2002-2017 Ulm University, Othmar Marti, pict

Lizenzinformationen