©2002-2017 Ulm University, Othmar Marti, 
[Nächste
Seite] [Vorherige Seite] [vorheriges Seitenende] [Seitenende]
[Ebene nach oben] [PDF-Datei][Epub-Datei][Andere
Skripte]
2.4 Kontinuierliche und diskrete Signale
Signale und Signalformen sind wesentlich zum Verständnis
physikalischer Messsysteme. Generell werden Signale in zwei
Kategorien aufgeteilt:
- Kontinuierliche Signale
- Zeitbegrenzte Signale
Die erste Kategorie von Signalen kann sowohl in der
Zeitdomäne wie auch in der Frequenzdomäne behandelt
werden. Die zweite Kategorie wird bevorzugt in der
Zeitdomäne diskutiert. Genau genommen gibt es keine
periodischen Signale, da nie eine unendliche Messzeit möglich
ist. In der Frequenzdomäne wird vorwiegend mit der
Fourier-Transformation gearbeitet. Die Fourier-Transformation
setzt unendlich dauernde Signale voraus. Diese Signale
verletzen aber die Kausalität. Um dieses Problem zu
lösen verwendet man in der Regel in der Elektronik die
Laplace-Transformation.
2.4.1 Signale
2.4.1.1. Periodische Signale
Eine erste Gruppe von Signalen sind die periodischen
Signale. Diese können auf Summen von Sinus- oder
Cosinus-Funktionen zurückgeführt werden. Typische, in
der Elektronik vorkommende periodische Signale sind:
- Harmonische Funktionen:
sin(ωt) und cos(ωt)
- Rechteckfunktion:
f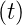 =
=
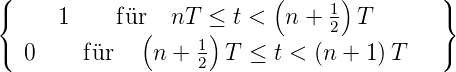 n ∈
Z
n ∈
Z
- Impulsfunktion:
f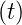 =
=
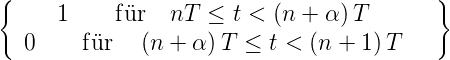 n ∈
Z; 0 ≤α < 1
n ∈
Z; 0 ≤α < 1
- Dreiecksfunktion:
f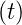 =
= 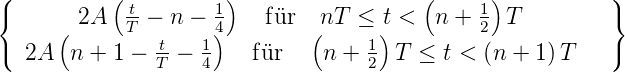 n ∈
Z
n ∈
Z
- Sägezahnfunktion:
f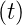 = A
= A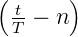 für nT ≤ t <
für nT ≤ t <
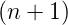 T; n ∈Z
T; n ∈Z
2.4.1.2. Einmalige Signale, Einschalt- und Ausschaltvorgänge
Einmalige Funktionsverläufe treten auf, wenn ein Gerät
eingeschaltet oder ausgeschaltet wird. Als Beispiel kann man
die Ladekurve eines Kondensators C betrachten, wenn er über
einen Widerstand R an eine Spannungsquelle U angeschlossen
wird. Zur Zeit t = 0 soll die Verbindung eingeschaltet werden.
Wir haben dann die folgenden Situation für UC, die Spannung
am Kondensator.
Die resultierende Funktion ist klar nicht periodisch.
Genau genommen gibt es nur nichtperiodische Signale,
da alle periodischen eine unendlich lange Dauer haben
müssten.
2.4.1.3. Diskrete Signale
Ein typisches Beispiel für diskrete Signale ist die
Treppenfunktion. Sie ist wie folgt definiert:
Die Treppenfunktion generiert aus der Folge 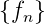 kann in realen Schaltungen gut implementiert werden.
Mathematisch einfacher zu handhaben ist jedoch der
Dirac-Kamm:
kann in realen Schaltungen gut implementiert werden.
Mathematisch einfacher zu handhaben ist jedoch der
Dirac-Kamm:
Der Dirac-Kamm erlaubt ein einfaches rechnen, da eine
Integration mit Hilfe der δ-Funktion sofort gelöst werden
kann.
2.4.1.4. Digitale Signale
Eine Sonderklasse der diskreten Signale sind die digitalen
Signale, wie sie in der Computertechnik vorkommen. Die
digitalen Signale haben zwei Werte, 0 oder 1. Diese Werte
sind in Logikpegel kodiert. So ist bei der TTL-Logik der
Nullwert 0V < x < 0.8V und der 1-Pegel 2V < x < 5V .
Digitale Signale werden mit logischen Schaltungen verknüpft.
Ihre Schaltpegel sind definiert, eine Schaltung für digitale
Signale darf nur mit den entsprechenden Pegelwerten
betrieben werden, so dass keine undefinierten Zustände
auftreten.
Heute werden in ausgewählten Anwendungsbereichen
Logiken mit weichen Übergängen zwischen den einzelnen
Zuständen verwendet. Diese Fuzzy-Logiken ermöglichen
Aussagen wie: Es ist ein bisschen kalt, oder, es ist ein
wenig zu warm. Gleitend definierte Übergänge zwischen
Schaltzuständen sind vor allem bei schlecht in Zahlen
fassbaren Problemen von Vorteil.
2.4.2 Fourier-Transformationen
Periodische Signale f(t) = f(t+T) können als Reihenentwicklung
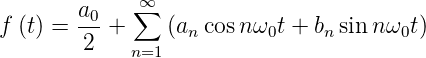 | (2.4) |
geschrieben werden. Die Koeffizienten der Reihenentwicklung
können wie folgt berechnet werden:
Alternativ kann eine komplexe Darstellung gewählt werden.
Die Funktion heisst dann:
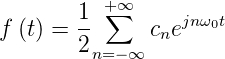 | (2.6) |
Auch hier können die cn mit einer Integralformel berechnet
werden:
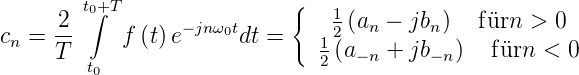 | (2.7) |
Die Fourierkoeffizienten einer Funktion heissen das
Amplitudenspektrum. Da die Sinus- und Cosinusfunktionen der
Frequenz ω0 zusammen ein orthogonales Funktionensystem
bilden, kann jede periodische Funktion dieser Frequenz
eindeutig dargestellt werden. Die Amplitudenspektren haben
die folgenden Eigenschaften:
- Je schnellere Änderungen des Signals auftreten, desto
grösser sind die höheren Fourierkoeffizienten.
- Eine Funktion f(t) wird durch eine trigonometrische
Reihe
sm
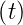 =
= 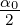 +∑
n=1mα
n cos nω0t+∑
n=1mβ
n cos nω0t
approximiert. Dann ist der quadratische Fehler
δ2 =
+∑
n=1mα
n cos nω0t+∑
n=1mβ
n cos nω0t
approximiert. Dann ist der quadratische Fehler
δ2 = 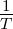 ∫
0T
∫
0T ![[f (t) − sm (t)]](phys_elektr47x.png) 2dt minimal, wenn die
Koeffizienten αn und βn die Fourierkoeffizienten
sind.
2dt minimal, wenn die
Koeffizienten αn und βn die Fourierkoeffizienten
sind.
- Für jede beschränkte und im Intervall 0 <
t < T stückweise stetige Funktion konvergiert die
Fourierreihe im Mittel gegen die gegebene Funktion.
- Ist eine
Funktion einschliesslich ihrer k-ten Ableitung stetig,
dann streben für n → ∞ auch annk+1 und b
nnk+1
gegen null.
- Ist f(t) eine gerade Funktion, das heisst f(−t) =
f(t), so gilt: bn = 0
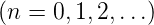 . Dies ist die
Symmetrie erster Art.
. Dies ist die
Symmetrie erster Art.
- Wenn f(t) ungerade ist, das heisst, f(−t) = −f(t),
dann gilt: an = 0
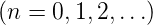 . Dies ist die
Symmetrie zweiter Art.
. Dies ist die
Symmetrie zweiter Art.
- Gilt f
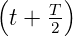 = −f(t), dann sind a2n =
b2n = 0
= −f(t), dann sind a2n =
b2n = 0 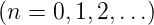 . Dies ist die Symmetrie
dritter Art.
. Dies ist die Symmetrie
dritter Art.
- Besitzt eine ungerade Funktion die Symmetrie
dritter Art (Symmetrie vierter Art), dann gilt
an = b2n = 0
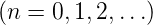 .
.
- Besitzt eine gerade Funktion die Symmetrie dritter
Art (Symmetrie vierter Art), dann gilt a2n =
bn = 0
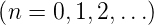 .
.
Mit Hilfe der oben gezeigten Symmetrien kann sehr
schnell der Oberwellengehalt einer Funktion abgeschätzt
werden.
Für nichtperiodische Signale oder für Ausschnitte aus
periodischen Signalen verwendet man die Fouriertransformation
anstelle der Fourierreihe. Die Fouriertransformation und ihre
Rücktransformation sind wie folgt definiert:
F(ω) ist die spektrale VerteilungsfunktionKreisfrequenz
eines Signals. Damit sie existiert, muss das Integral
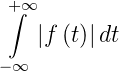 | (2.10) |
endlich sein. Als Beispiel berechnen wir das Spektrum eines
Rechteckimpulses. Der Impuls ist gegeben durch
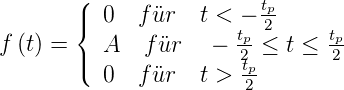 | (2.11) |
Das Spektrum wird dann
Das Spektrum F ist reell. Dies ist eine Konsequenz der
Tatsache, dass f(t) eine gerade Funktion ist. Wäre f(t)
eine ungerade Funktion, dann wäre das Spektrum rein
imaginär. Die grössten Amplituden in F sind auf den Bereich
0 ≤f = 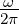 ≤
≤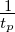 beschränkt. B =
beschränkt. B = 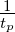 heisst die Bandbreite des
Impulses. Allgemein gilt für Pulse
heisst die Bandbreite des
Impulses. Allgemein gilt für Pulse
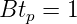 | (2.15) |
Je kürzer also ein Puls ist,desto grösser ist seine Bandbreite.
Für einen unendlich scharfen Puls, einen Dirac-δ-Puls
bedeutet dies, dass seine Spektralfunktion konstant ist. Dieses
Gesetz hat eine Ähnlichkeit mit den Unschärferelationen der
Quantenmechanik.
Wiener-Khintchine-Relationen
Die Wiener-Khintchine-Relationen verknüpfen die
Autokorrelationsfunktion mit dem Leistungsspektrum eines
Signals. Wir definieren die Korrelationsfunktion K(s) der
Funktion y(t) als das Ensemblemittel
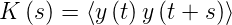 | (2.16) |
Die Grösse
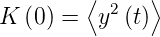 | (2.17) |
ist offensichtlich die Varianz von y(t), wenn s = 0 ist. Wie
jede Funktion kann auch K(s) als Fourierintegral geschrieben
werden
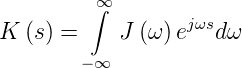 | (2.18) |
J(ω) ist das Leistungsspektrum oder die Spektrale Dichte
der Funktion y(t). Die Fouriertransformation in Gleichung
(2.18) kann umgekehrt werden.
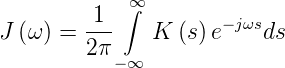 | (2.19) |
Die Gleichungen (2.18) und (2.18) Sind die
Wiener-Khintchine-Relationen. Die Relation kann bewiesen
werden, indem man in Gleichung (2.18) von rechts mit e−jω′s
multipliziert und über s integriert.
Die Korrelationsfunktion K(s) ist reell und gerade, also
eine Symmetrie erster Art. Deshalb würden bei einer
Fourierreihe nur cos-Terme auftreten. Hier bedeutet dies, dass
J(ω) auch reell und gerade ist, also
Die beiden Relationen können bewiesen werden, indem man
Gleichung (2.19 anwendet und dann die Integrationsvariable
von s nach −s ändert. Gleichung (2.18) kann umgeschrieben
werden
Die Fourierintegrale können wegen den Symmetrieeigenschaften
auch als cos-Transformationen geschrieben werden. Man setzt
e±jωs = cos ωs ±j sin ωs und erhält (da sin ungerade
ist)
K(s) und J(ω) können direkt aus den Fourierkoeffizienten
von y(t) berechnet werden. Wenn y(t) stationär und ergodisch
ist, ist K(s) zeitunabhängig und das Ensemblemittel 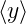 kann
durch das Zeitmittel
kann
durch das Zeitmittel 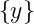 ersetzt werden (Die Definitionen
finden Sie in Reif [Rei65] Kapitel 15.14 oder im Anhang K).
Dies gilt für periodische Funktionen, muss aber für statistisch
schwankende Funktionen wie das Rauschen gefordert
werden. Gleichung (2.18) kann nun geschrieben werden
als
ersetzt werden (Die Definitionen
finden Sie in Reif [Rei65] Kapitel 15.14 oder im Anhang K).
Dies gilt für periodische Funktionen, muss aber für statistisch
schwankende Funktionen wie das Rauschen gefordert
werden. Gleichung (2.18) kann nun geschrieben werden
als
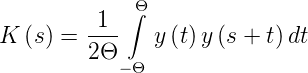 | (2.24) |
Wir setzen
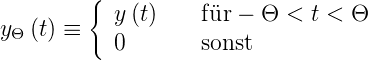 | (2.25) |
und erhalten für K(s)
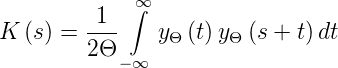 | (2.26) |
Durch die Ersetzung von y(t) mit y − Θ(t) führt man
einen Fehler der Grössenordnung 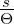 ein, der für Θ →∞
verschwindet. Mit
ein, der für Θ →∞
verschwindet. Mit
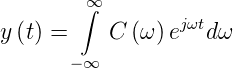 | (2.27) |
(C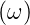 ist die Fouriertransformation von y(t)) erhält
man
ist die Fouriertransformation von y(t)) erhält
man
Setzt man
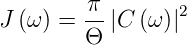 | (2.29) |
so erhält man Gleichung (2.18). Durch diese Rechnung
wird klar, dass J(ω) das Leistungsspektrum ist. Die
Wiener-Khintchine-Relationen lassen sich wie folgt
zusammenfassen:
Die Autokorrelation und das
Leistungssprektrum sind
Fouriertransformierte
Zum Schluss sei angemerkt, dass
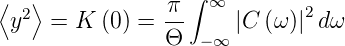 | (2.30) |
ist.
2.4.3 Laplace-Transformationen
Die Fouriertransformation im vorangegangenen Kapitel kann
nur gelöst werden, wenn das Integral über den Betrag der
Zeitfunktion endlich ist. Weiter müssen die Funktionswerte zu
allen früheren, aber auch zu allen späteren Zeiten bekannt
sein. Damit ist die Fouriertransformation akausal. Die
Kausalität verlangt nun, dass ein Signal nur von seiner
Vorgeschichte, nicht aber von seiner Zukunft abhängen kann.
Eine Konsequenz der Kausalität ist, dass es keine beliebig
scharfen Filter geben kann.
Mit der Laplace-Transformation kann insbesondere sehr
elegant das Problem der Berechnung von Faltungsintegralen
gelöst werden. Dieses Problem taucht immer dann auf, wenn
Ein Ausgangssignal bei bekannter Impulsantwort aus dem
Eingangssignal berechnet werden muss.
Die Laplace-Transformation ist nun definiert durch
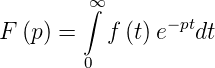 | (2.31) |
Hier ist p = x + jω eine komplexe Funktion. Wenn f(t) = 0 ist
für t < 0 dann ist in vielen Fällen die Fouriertransformation
und die Laplace-Transformation äquivalent. Vielfach schreibt
man für die Laplace-Transformation auch
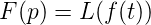 | (2.32) |
Die Umkehrfunktion der Laplace-Transformation ist nicht
so einfach wie die der Fouriertransformation. Während bei
dieser ein Vorzeichen gewechselt werden muss, benötigt die
Laplace-Transformation eine Integration in der komplexen
Ebene.
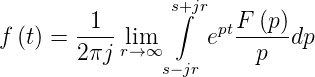 | (2.33) |
dabei muss der Integrationsweg s so gewählt werden, dass
alle singulären Punkte des Integranden links von der
Geraden ℜp = s liegen. Die wichtigsten Eigenschaften der
Laplace-transformierten Funktion sind:
- L
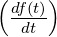 = pF
= pF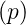 −f
−f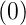
- L
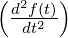 = p2F
= p2F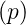 −pf
−pf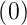 −f′
−f′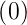
- L
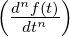 = pnF
= pnF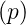 −p
−p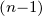 f
f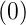 −p
−p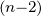 f′
f′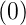 −…−
f
−…−
f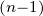
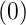
- L
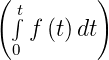 =
= 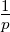 F
F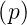
- L
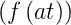 =
=  F
F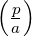
- Wenn L
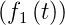 = F1
= F1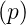 und L
und L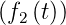 = F2
= F2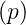 ist,
dann ist auch L
ist,
dann ist auch L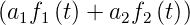 = a1F1
= a1F1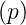 +
a2F2
+
a2F2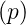
- Dämpfungssatz: Wenn L
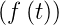 = F
= F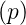 , dann ist
L
, dann ist
L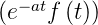 = F
= F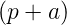
- Verschiebungssatz nach rechts (Retardation): Wenn
L
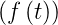 = F
= F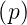 und λ > 0, dann ist L
und λ > 0, dann ist L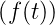 =
e−λpF(p)
=
e−λpF(p)
- Verschiebungssatz nach links: Wenn L
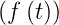 =
F
=
F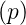 und λ > 0, dann ist L
und λ > 0, dann ist L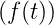 =
eλp
=
eλp![[ ∫ λ −pt ]
F (p) − 0 e f(t)dt](phys_elektr122x.png)
- Satz von Borel: Wenn L
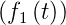 = F1
= F1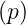 und L
und L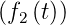 = F2
= F2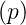 ist, dann ist auch
L
ist, dann ist auch
L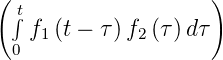 =
= 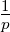 F1
F1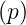 F2
F2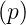
- Die Ausgangsfunktion zu F(p) = p ist die
Dirac-δ-Funktion
Die Laplace-Transformation wird eingesetzt, um
Differentialgleichungssysteme zu lösen. In der Elektronik wird
Sie zur Berechnung von Frequenzgängen verwendet.
Einige Funktionen und ihre Laplacetransformierten sind in
der Tabelle C.1 im Anhang angegeben.
Beispiel (Maple-Datei): Laplace-Transformation
(Maple)
2.4.4 z-Transformationen
Die obigen Transformationen, die Fouriertransformation
(Abschnitt 2.4.2) und die Laplace-Transformation (Abschnitt
2.4.3), können nur auf kontinuierliche Signale angewandt
werden. Digitale Signalverarbeitung funktioniert aber nur
mit zeit- und amplitudendiskreten Messwerten. Die hier
besprochene z-Transformation ist die für dieses Problem
angepasste Transformation. Die z-Transformation und die im
Abschnitt 2.6.2 besprochenen Digitalfilter und -techniken
können auch auf die Datenanalyse im Computer angewandt
werden. Während die Laplace-Transformation und die
Fourier-Transformation zur Lösung von Differentialgleichungen
und -gleichungssystemen verwendet werden können, wird die
z-Transformation zur Berechnung von Systemen von
Differenzengleichungen verwendet.
Wir betrachten nun eine Übertragungskette für diskrete
Signale (Abbildung 2.20 und 2.21).
Hier ist die Funktion f(t) für die Zeiten 0 < t < ∞ nur für
diskrete Argumente tn = nTa 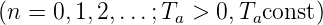 definiert. Die Amplitudenwerte an den diskreten Zeitwerten
sind ebenfalls diskret. Die Folge
definiert. Die Amplitudenwerte an den diskreten Zeitwerten
sind ebenfalls diskret. Die Folge 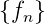 und die an diskreten
Zeitwerten definierte Funktion f(nTa) sind äquivalent.
und die an diskreten
Zeitwerten definierte Funktion f(nTa) sind äquivalent.
Die z-Transformation F(z) der Folge 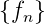 ist definiert
durch
ist definiert
durch
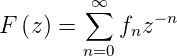 | (2.34) |
Die Folge 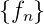 heisst z-transformierbar, wenn die Summe
in Gleichung (2.34) konvergiert. Als Kürzel kann man auch
schreiben
heisst z-transformierbar, wenn die Summe
in Gleichung (2.34) konvergiert. Als Kürzel kann man auch
schreiben
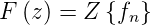 | (2.35) |
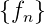 ist die Originalfolge, F(z) die Bildfolge.
ist die Originalfolge, F(z) die Bildfolge.
Ein Beispiel
Sei fn = 1,(n = 0, 1, 2, 3,…). Die z-Transformation
ist
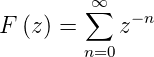 | (2.36) |
Die Summe in Gleichung (2.36 ist bezüglich  eine
geometrische Reihe. Sie konvergiert gegen
eine
geometrische Reihe. Sie konvergiert gegen 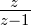 , wenn
, wenn  < 1 ist.
Das heisst aber, dass die Folge
< 1 ist.
Das heisst aber, dass die Folge 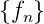 z-transformierbar ist für
alle z-Werte ausserhalb des Einheitskreises
z-transformierbar ist für
alle z-Werte ausserhalb des Einheitskreises 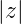 > 1.
> 1.
Eigenschaften
2.4.4.1. Rechenregeln für die z-Transformation
Wir gehen von der Folge 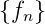 und ihrer z-Transformierten
Z
und ihrer z-Transformierten
Z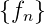 = F(z) aus
= F(z) aus
-
1. Verschiebungssatz
-
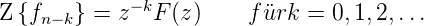 | (2.42) |
-
2. Verschiebungssatz
-
![[ ]
k k∑−1 − ν
Z {fn+k } = z F (z) − fνz f¨urk = 1,2,3,...
ν=0](phys_elektr162x.png) | (2.43) |
-
Summation
- Für
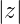 > max
> max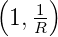 gilt:
gilt:
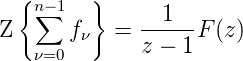 | (2.44) |
-
Differenzenbildung
- Für die Differenzen
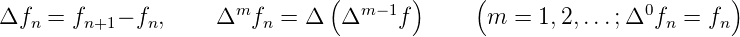 gilt:
gilt:
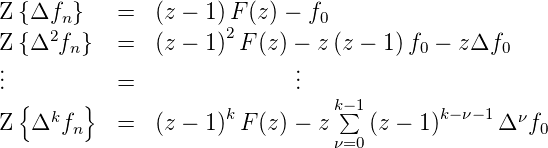 | (2.45) |
-
Dämpfung
- für λ ⇔ 0 beliebig komplex und
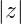 >
> 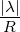 gilt
gilt
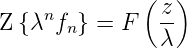 | (2.46) |
-
Faltung
- Als Faltung der Folgen
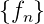 und
und 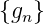 bezeichnet
man
bezeichnet
man
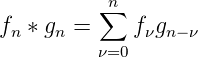 | (2.47) |
Existieren Z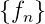 = F(z) für
= F(z) für 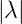 >
> 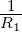 und Z
und Z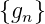 = G(z)
für
= G(z)
für 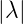 >
> 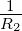 dann ist
dann ist
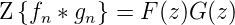 | (2.48) |
Die in Gleichung (2.48 definierte Faltung konvergiert für
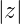 > max
> max 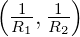 . Dieser Faltungssatz ist analog zu
den Faltungssätzen für die Fouriertransformation und
die Laplace-Transformation.
. Dieser Faltungssatz ist analog zu
den Faltungssätzen für die Fouriertransformation und
die Laplace-Transformation.
-
Differentiation der Bildfunktion
-
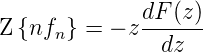 | (2.49) |
Höhere Ableitungen lassen sich analog bilden.
-
Integration der Bildfunktion
- Falls f0 = 0 gilt
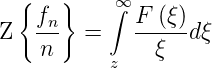 | (2.50) |
2.4.4.2. z-Transformation und Laplace-Transformation
Die diskrete Funktion f(t) kann auch als Treppenfunktion
geschrieben werden:
Hier ist TA die Abtastzeit.
Die Laplace-Transformierte dieser Funktion ist (Siehe auch
Gleichungen (2.31) und (2.32)).
Die unendliche Folge wird auch als diskrete
Laplace-Transformation bezeichnet.
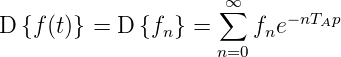 | (2.53) |
Ersetzt man in der Gleichung (2.53) eTAp durch z (dies ist
der Ursprung der Bezeichnung z-Transformation) erhält man
für Treppenfunktionen die Beziehung
Mit Hilfe der Beziehungen in Gleichungen (2.54) und (2.55)
kann man aus den Laplace-Transformationen in Tabelle
C.1 die entsprechenden z-Transformationen ausrechnen.
2.4.4.3. Rücktransformation
Die Rücktransformation
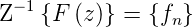 | (2.56) |
der z-Transformation kann mit vier verschiedenen Methoden
berechnet werden.
- Benutzung von Tabellen
- Berechnung der Laurent-Reihe von F(z)
- Berechnung der Taylor-Reihe von F
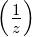 . Es ist
. Es ist
 | (2.57) |
- Anwendung eines Grenzwertsatzes
Beispiel
Es soll die zu F(z) = 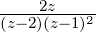 gehörige Folge berechnet
werden.
gehörige Folge berechnet
werden.
- Aus der Partialbruchzerlegung von
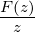 erhält man
erhält man
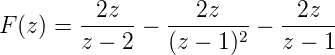 | (2.58) |
und somit
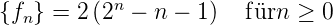 | (2.59) |
- Entwicklung in Potenzen von

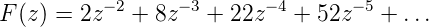 | (2.60) |
Daraus kann man direkt die Folge 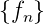 ablesen.
Einen geschlossenen Ausdruck erhält man jedoch
nicht.
ablesen.
Einen geschlossenen Ausdruck erhält man jedoch
nicht.
- Man berechne die Ableitungen von F
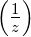
Berücksichtigt man, dass die Koeffizienten der
Taylor-Entwicklung noch mit n! normiert sind, erhält
man ein konsistentes Resultat für 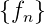 .
.
- Aus den Grenzwertsätzen erhält man
2.4.5 Anwendung der Transformationen auf Einschaltvorgänge
Um Einschaltvorgänge zu untersuchen werden entweder die
Stoss- oder Sprungantwort untersucht. Die Sprungantwort ist
die Antwort des Systems auf die Sprungfunktion
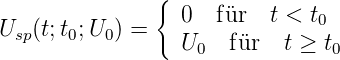 | (2.63) |
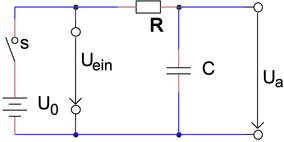
am Eingang. Als erstes Beispiel berechnen wir die
Ausgangsspannung an einem RC-Glied, wenn am Eingang
eine Sprungfunktion angelegt wird (Abbildung 2.22).
Unter der Voraussetzung, dass zur Zeit t = 0 der Kondensator
entladen ist, erhält man mit Uein = IR + Ua und der
Beziehung I = 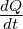 = C
= C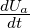 die Differentialgleichung
die Differentialgleichung
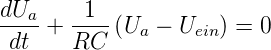 | (2.64) |
Die Lösung dieser elementaren Differentialgleichung unter
Berücksichtigung der Anfangsbedingungen ist
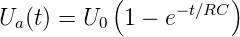 | (2.65) |
Die Lösung, und damit die zeitliche Übertragungsfunktion oder
Einheitsschrittantwort 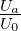 ist die bekannte Exponentialfunktion.
ist die bekannte Exponentialfunktion.
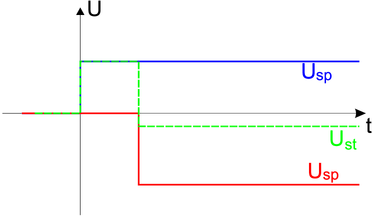
Im Allgemeinen besteht das Einschaltsignal aus einer
Kombination einer Stossfunktion und einer Sprungfunktion,
wie sie Abbildung 2.23 zeigt. Wenn wir annehmen, dass für
t < 0 Ue = 0 gilt, dann für 0 ≥t < Δt der Wert Ue = Ust und
für t ≥ Δt Ue = U∞ ist, kann die Eingangsfunktion mit
Gleichung (2.63 als
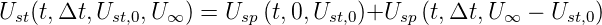 | (2.66) |
geschrieben werden. Unter der Voraussetzung, dass
- die Schaltung stabil ist
- das Überlagerungsgesetz gilt und
- die Sprungantwort unabhängig vom Zeitpunkt des
Sprunges ist
lässt sich die Stossantwort mit U∞ = 0 berechnen.
Die obige Gleichung zeigt, dass bei einer stossförmigen
Anregung immer eine sofortige Antwort sowie eine langzeitliche
Antwort vorhanden ist.
Wenn die Eingangsfunktion mathematisch nicht trivial ist,
kann man sie in eine Folge von Stossfunktionen geschrieben
werden.
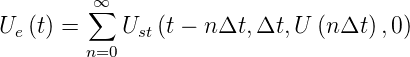 | (2.68) |
Wir modifizieren die obige Gleichung
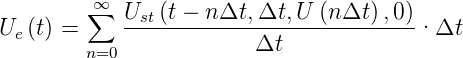
Durch den Grenzübergang Δt → 0 wird die obige Gleichung
zu einem Integral, wobei 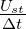 die Diracsche Deltafunktion δ(t)
approximiert
die Diracsche Deltafunktion δ(t)
approximiert
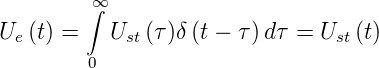 | (2.69) |
einem Faltungsintegral, das gelöst werden kann. Aus der
Stossantwort Ua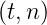 einer einzelnen Stossfunktion erhält
man die Antwort des gesamten Systems
einer einzelnen Stossfunktion erhält
man die Antwort des gesamten Systems
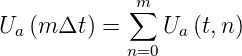 | (2.70) |
Wenn A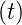 = lim Δt→0
= lim Δt→0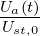 die zeitliche Übertragungsfunktion
eines Einheitsschrittes ist, muss man, um zur Stossantwort
(der Reaktion des Systems auf einen Dirac’schen Deltapuls
δ(t) zu kommen, die folgende Umrechnung machen.
die zeitliche Übertragungsfunktion
eines Einheitsschrittes ist, muss man, um zur Stossantwort
(der Reaktion des Systems auf einen Dirac’schen Deltapuls
δ(t) zu kommen, die folgende Umrechnung machen.
Wenn Θ(t) die Heaviside-Funktion ist, also ein Einheitssprung,
gilt, dass
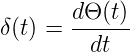
wenn also A(t) die Systemantwort auf eine Sprungfunktion ist,
dann ist 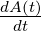 bei einem linearen System die Systemantwort
auf einen Deltapuls. Also wird die Sytemantwort auf einen
beliebigen Eingang das Faltungsintegral
bei einem linearen System die Systemantwort
auf einen Deltapuls. Also wird die Sytemantwort auf einen
beliebigen Eingang das Faltungsintegral
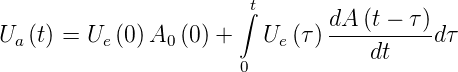 | (2.71) |
Legt man beispielsweise an die Schaltung aus Abbildung 2.22
eine exponentiell ansteigende Spannung Ue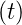 = U0
= U0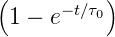 an und berücksichtigt, dass aus Gleichung (2.65)
an und berücksichtigt, dass aus Gleichung (2.65)
Die Antwortfunktion ist
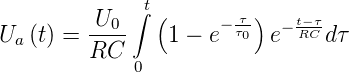 | (2.73) |
Wenn die Eingangsspannung die gleiche Zeitkonstante
wie die RC-Schaltung hat, also RC = τ0, dann ergibt
sich
![U0 − t-∫t( τ- ) [ ( t ) − t-]
Ua (t) = --e τ0 e τ0 − 1 dτ = U0 1 − 1 + -- e τ0
τ0 0 τ0](phys_elektr228x.png) | (2.74) |
Es gibt die einfache Beziehung zwischen der
Fouriertransformation und einem Faltungsintegral:
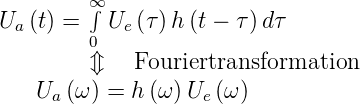 | (2.75) |
Ein weiteres illustratives Beispiel ist das Anlegen einer
Wechselspannung U0 sin ωt an eine Spule (Siehe Abbildung
2.17). Für t > 0 gilt die Differentialgleichung
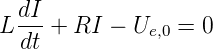 | (2.76) |
Die Lösung dieser Gleichung, sowie die zeitliche
Übertragungsfunktion sind
Mit
bekommt man für den Strom
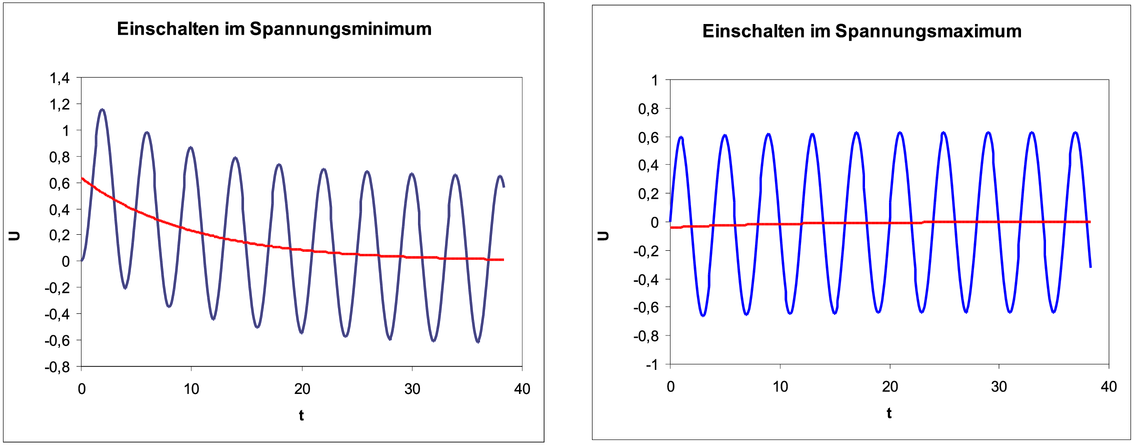
Schaltet man bei der Maximalspannung ein, ergibt sich
Wie aus Abbildung 2.25 (Excel-Tabelle) ersichtlich, wird
der Dauerzustand sehr viel schneller erreicht, wenn man bei
der Maximalspannung eine Spule an eine Wechselspannung
als wenn man im Nulldurchgang schaltet. Der Grund ist
der Folgende: Die Anfangsbedingung der allgemeinen
Lösung hängt von der Grösse der speziellen Lösung zum
Anfangszeitpunkt ab. Da bei einer Spule der Strom im
Dauerzustand 900 ausser Phase ist, muss bei einem Einschalten
im Nulldurchgang die Anfangsbedingung der allgemeinen
Lösung den maximalen Strom kompensieren. Wenn bei der
maximalen Spannung eingeschaltet wird, ist der Strom null,
die Anfangsbedingung der allgemeinen Lösung ist also auch
null. Je weniger die Spule durch den Quellwiderstand
gedämpft wird, desto ausgeprägter ist der Effekt, dass die Zeit
zum Erreichen des Gleichgewichtszustandes im ersten Fall
grösser ist.
Beispiel (HTML-Datei): Anwendung der z-Transformation
Beispiel (PDF-Datei): Anwendung der z-Transformation
Beispiel (Maple-Datei): Berechnung der z-Transformation
2.4.6 Digitale Signale
Digitale Signale, also 0 oder 1, werden mit logischen
Schaltungen verknüpft. Digitale Signale werden mit Hilfe von
Zahlensystemen auf unsere Werteskale der natürlichen Zahlen
abgebildet. Gebräuchlich sind:
- Das binäre Zahlensystem, bestehend aus
Dualzahlen. 10110B, "B"nachgestellt.
- Das
Oktalsystem. 234O oder 234Q , O (der Buchstabe,
Verwechslungsgefahr) oder Q nachgestellt
- das Hexadezimalsystem. 3FH oder $3F, H
nachgestellt oder $ vorangestellt
- das Dezimalsystem. 123D, D nachgestellt
|
|
|
|
| Dual (binär) | Dezimal | Oktal | Hexadezimal |
|
|
|
|
| 000 000 = 0000 | 0 | 0 | 0 |
| 000 001 = 0001 | 1 | 1 | 1 |
| 000 010 = 0010 | 2 | 2 | 2 |
| 000 011 = 0011 | 3 | 3 | 3 |
| 000 100 = 0100 | 4 | 4 | 4 |
| 000 101 = 0101 | 5 | 5 | 5 |
| 000 110 = 0110 | 6 | 6 | 6 |
| 000 111 = 0111 | 7 | 7 | 7 |
| 001 000 = 1000 | 8 | 10 | 8 |
| 001 001 = 1001 | 9 | 11 | 9 |
| 001 010 = 1010 | 10 | 12 | A |
| 001 011 = 1011 | 11 | 13 | B |
| 001 100 = 1100 | 12 | 14 | C |
| 001 101 = 1101 | 13 | 15 | D |
| 001 110 = 1110 | 14 | 16 | E |
| 001 111 = 1111 | 15 | 17 | F |
|
|
|
|
| |
| Tabelle 2.4.: | Vergleich der Zahlensysteme |
In Tabelle 2.4 haben wir, wie üblich für die Ziffern "10" bis
"15" die Buchstaben A…F verwendet. Eine schöne Übersicht
über die Grundlagen der Digitaltechnik findet man im Buch
von Häßler und Straub[HS93].
2.4.6.1. Logische Verknüpfungen
| Tabelle 2.5.: | Logische Verknüpfungen mit einer
Eingangsvariablen |
Nicht-Gatter
Die Grundverknüpfungen mit einer Variable sind in Tabelle
2.5 angegeben. Die Verknüpfungen (1) und (2) haben keinen
praktischen Nutzen. (3) ist die Funktion eines Buffers
während (4) eine Negation darstellt. Die Logiktafel der
Negation sowie die Schaltbilder und die Signalformen sind in
Abbildung 2.26 dargestellt. Man schreibt die Negation
üblicherweise
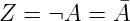 | (2.81) |
Und-Gatter
Die erste der zweiwertigen Funktionen ist das Und-Gatter.
Sein Ausgang ist eins, genau wenn beide Eingänge auf eins
sind. Die Logiktafel des Und-Gatters sowie die Schaltbilder
und die Signalformen sind in Abbildung 2.27 dargestellt. In
Formeln stellt man die Konjunktion (Und) wie folgt
dar:
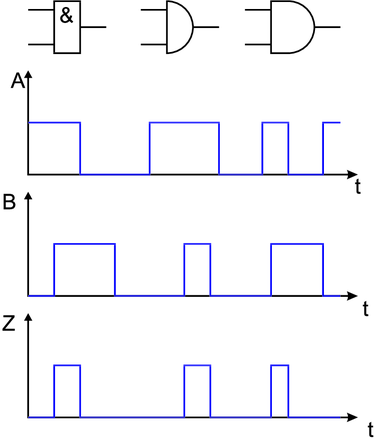
Oder-Gatter
Die zweite der zweiwertigen Grundfunktionen ist das
Oder-Gatter. Sein Ausgang ist eins, wenn mindestens
einer der beiden Eingänge auf eins ist. Die Logiktafel des
Oder-Gatters sowie die Schaltbilder und die Signalformen sind
in Abbildung 2.28 dargestellt. In Formeln stellt man die
Disjunktion (Oder) wie folgt dar:
Mit den Verknüpfungen UND, ODER und NICHT
können alle logischen Verknüpfungen erzeugt werden. Es hat
sich aber herausgestellt, dass einige andere abgeleitete
Verknüpfungen einfacher in Silizium zu bauen sind. Mit einer
Auswahl abgeleiteter Funktionen lassen sich ebenso alle
Verknüpfungen herstellen.
NAND-Gatter
Eine häufig verwendete abgeleitete Verknüpfung ist das
NAND-Gatter. Sein Name ist Abgeleitet aus NOT und AND.
Sein Ausgang ist eins, wenn einer der beiden Eingänge nicht
auf eins ist. Die Logiktafel des NAND-Gatters sowie die
Schaltbilder und die Signalformen sind in Abbildung 2.29
dargestellt. In Formeln stellt man die NAND-Funktion wie
folgt dar:
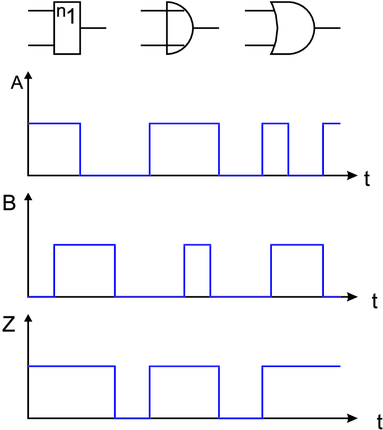
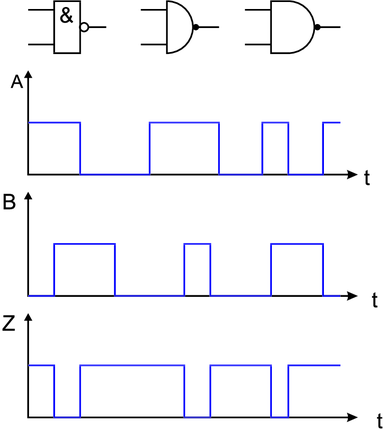
NOR-Gatter
Eine weitere häufig verwendete abgeleitete Verknüpfung ist
das NOR-Gatter. Sein Name ist abgeleitet aus NOT und OR.
Sein Ausgang ist eins, wenn beide Eingänge nicht auf eins
sind. Die Logiktafel des NOR-Gatters sowie die Schaltbilder
und die Signalformen sind in Abbildung 2.30 dargestellt.
In Formeln stellt man die NAND-Funktion wie folgt
dar:
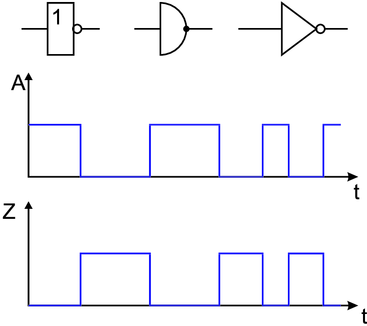
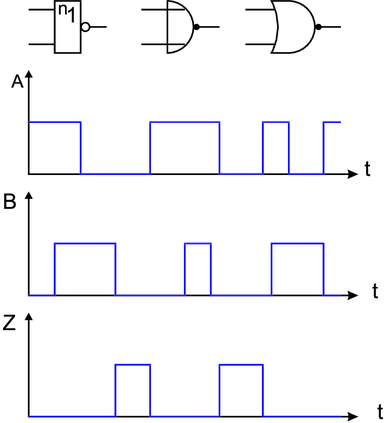
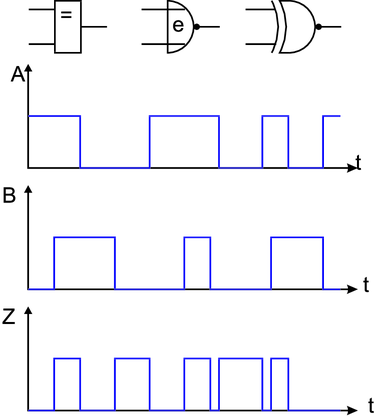
Äquivalenzgatter
Eine weitere abgeleitete Verknüpfung ist das Äquivalenz-Gatter.
Sein Ausgang ist eins, wenn beide Eingänge auf gleichem Pegel
sind. Die interne Funktion kann wie in Tabelle 2.6 gezeigt,
abgeleitet werden. Die Logiktafel des Äquivalenz-Gatters sowie
die Schaltbilder und die Signalformen sind in Abbildung 2.31
dargestellt. In Formeln stellt man die Äquivalenz-Funktion wie
folgt dar:
| A | B | A | B | Q = A ∧B | S = A ∧B | Z = Q ∨S |
|
|
|
|
|
|
|
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| |
| Tabelle 2.6.: | Wahrheitstabelle des Äquivalenzgatters |
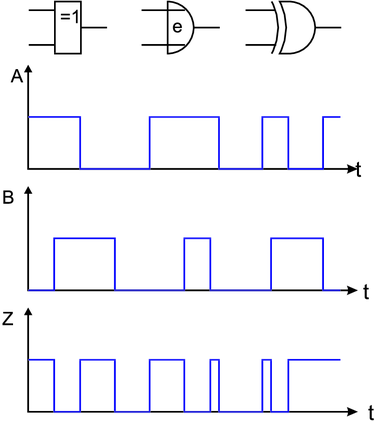
Antivalenzgatter oder XOR
Eine weitere abgeleitete Verknüpfung ist das Antivalenz-Gatter,
auch XOR-Gatter genannt. Der Name XOR ist eine
amerikanisch prägnante Abkürzung für eXclusive OR. Sein
Ausgang ist eins, wenn beide Eingänge auf verschiedenem
Pegel sind. Die Logiktafel des Antivalenz-Gatters sowie die
Schaltbilder und die Signalformen sind in Abbildung 2.32
dargestellt. In Formeln stellt man die Antivalenz-Funktion wie
folgt dar:
2.4.6.2. Boolesche Algebra, Schaltalgebra
Die Reihenschaltung von zwei Schaltern führt auf die
Verknüpfung UND. Die Parallelschaltung ergibt demnach
ODER. Dabei wird angenommen, dass der Schaltzustand 1
dem geschlossenen Schalter entspricht.
| UND | 0 ∧ 0 = 0 | 0 ∧ 1 = 0 | 1 ∧ 0 = 0 | 1 ∧ 1 = 1 |
| ODER | 0 ∨ 0 = 0 | 0 ∨ 1 = 1 | 1 ∨ 0 = 1 | 1 ∨ 1 = 1 |
| NICHT | 0 = 1 | 1 = 0 | | |
| |
| Tabelle 2.7.: | Postulate der Schaltalgebra |
In Tabelle 2.7 sind die Grundrechenregeln für Konstanten
zusammengefasst. Tabelle 2.8 zeigt die Theoreme der
Schaltalgebra. Dabei wird nun eine Variable, A, eingeführt,
deren Wert beliebig ist.
| UND | A ∧ 0 = 0 | A ∧ 1 = A | A ∧A = A | A ∧A = 0 |
| ODER | A ∨ 0 = A | A ∨ 1 = 1 | A ∨ A = A | A ∨ A = 1 |
| NICHT | 0 = 0 | 1 = 1 | | |
| |
| Tabelle 2.8.: | Theoreme der Schaltalgebra |
Wie bei den natürlichen oder ganzen Zahlen macht das
Kommutativgesetz eine Aussage über die Vertauschbarkeit
von Variablen bei der UND- oder ODER-Verknüpfung.
Analog gibt es auch ein Assoziativgesetz, das aussagt, dass
die Reihenfolge der Verknüpfung beliebig ist.
Auch für die Schaltalgebra gibt es Distributivgesetze. Man
unterscheidet das konjunktive Distributivgesetz
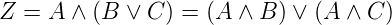 | (2.90) |
und das disjunktive Distributivgesetz
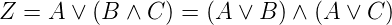 | (2.91) |
Zusätzlich zu den oben ausgeführten Gesetzen, die auch von
den üblichen Zahlensystemen her bekannt sind, gibt es die
deMorganschen Gesetze. Das erste DeMorgansche Gesetz
lautet
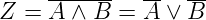 | (2.92) |
Die Gültigkeit dieses Gesetzes kann mit der Tabelle 2.9
gezeigt werden.
| A | B | A ∧B | A ∧B | A | B | A ∨B |
|
|
|
|
|
|
|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| |
| Tabelle 2.9.: | Wahrheitstabelle des ersten DeMorganschen
Gesetzes |
Das zweite DeMorgansche Gesetz lautet:
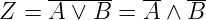 | (2.93) |
Die Gültigkeit dieses Gesetzes kann mit der Tabelle 2.10
gezeigt werden.
| A | B | A ∨B | A ∨B | A | B | A ∧B |
|
|
|
|
|
|
|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Tabelle 2.10.: | Wahrheitstabelle des zweiten
DeMorganschen Gesetzes |
Analog zum Rechnen mit ganzen Zahlen (als Beispiel) wird
definiert, dass UND stärker bindet als ODER (Punkt vor
Strich). damit erreicht man, dass nicht immer Klammern
gesetzt werden müssen, um die Reihenfolge der Ausführung
von Operationen festzulegen. Aus den DeMorganschen
Gesetzen folgt, dass jede UND-Verknüpfung mit ODER- und
NICHT-Verknüpfungen realisiert werden kann. Da man
immer eine NICHT-Verknüpfung aus einer NOR-Verknüpfung
erzeugen kann (entweder man legt einen Eingang auf
null, oder man verbindet beide Eingänge) benötigt man,
im Prinzip, nur NOR-Gatter, um eine gesamte Logik
aufzubauen. Diese Aussage mag, wenn man an integrierte
Schaltungen wie die 70LSxx-Reihe denkt, übertrieben klingen.
Wenn man eine grössere logische Schaltung jedoch mit
programmierbaren Logik-Array (PAL) aufbaut, dann hilft
einem die obige Aussage, um mit einem Typ Schaltungen alles
aufzubauen. Analog kann man auch zeigen, dass alle logischen
Schaltungen aus NAND-Verknüpfungen aufgebaut werden
können. Welche Verknüpfung man bevorzugt, hängt unter
anderem auch vom inneren Aufbau der Logikfamilien
ab.
Normalformen
Eine digitale Schaltung ist eindeutig durch ihre
Wahrheitstabelle gegeben. Aus der Wahrheitstabelle können
zwei Normalformen abgelesen werden.
-
ODER-(disjunktive) Normalform (DNF)
- Eine DNF ist
eine Oderverknüpfung von Vollkonjunktionen (nur
UND, jede Variable kommt nur einmal vor). Ziel
sind die Zustände 1. Die einzelnen Terme heissen
Minterm.
-
UND-(konjunktive) Normalform (KNF)
- Eine KNF ist
eine Undverknüpfung von Volldisjunktionen (nur
ODER, jede Variable kommt nur einmal vor). Ziel
sind die Zustände 0. Die einzelnen Terme heissen
Maxterm.
Eine DNF sieht dann so aus
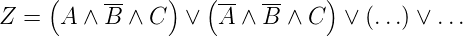 | (2.94) |
Entsprechend sieht eine KNF aus.
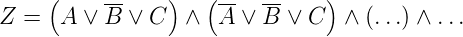 | (2.95) |
Tabelle 2.11 zeigt, wie man aus der Wahrheitstabelle die
DNF erzeugt. Man muss nur diejenigen Terme aufschreiben,
bei denen als Resultat in der Wahrheitstabelle eine 1
steht. Je weniger Einsen eine Wahrheitstabelle hat, desto
effizienter ist die DNF. Die KNF andererseits ist dann
anzuwenden, wenn im Ausgangsfeld nur wenige Nullen sind.
Tabelle 2.12 zeigt das entsprechende Vorgehen. In der
Tabelle wird gezeigt, dass man die DNF auf die negierte
Ausgangsvariable z anwendet. Die resultierende Form wird
negiert. Schliesslich werden die DeMorganschen Gesetze
angewendet. Die KNF wird also erhalten, indem man die
Zeilen heraus sucht, die z = 0 haben. Für jede dieser Zeilen
wird eine Disjunktion (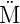 axterm
axterm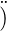 hingeschrieben, wobei
jede Variable mit
hingeschrieben, wobei
jede Variable mit 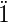 äls A, jede mit
äls A, jede mit 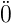 äls A geschrieben
wird.
äls A geschrieben
wird.
Eine weitergehende Übersicht über das Arbeiten mit
logischen Schaltungen kann in der Referenz [HS93] gefunden
werden.
2.4.6.3. Karnaugh-Diagramme
Karnaugh-Diagramme bieten eine weitere
Vereinfachungsmöglichkeit für logische Schaltnetzwerke. Wie
Abbildung 2.33 zeigt, kann aus einer Wahrheitstabelle das
Karnaugh-Diagramm abgeleitet werden. Dabei sind die
folgenden Regeln zu beachten:
- Die Wahrheitstabelle
wird zweidimensional angeordnet. Bei einer geraden
Anzahl von Eingangsvariablen enthalten Zeilen und
Spalten je die Hälfte der Variablen, sonst muss z.B.
die Spalten mehr Variablen enthalten.
- Die Variablen werden so angeordnet, dass sich von
einer Spalte (Zeile) zur nächsten nur eine Variable
ändert. Bemekung. Dies ist der Gray-Code.
- In die Felder werden die Werte der Resultatvariablen
y eingetragen.
Wir betrachten in Abbildung 2.34 die beiden Ausgangszellen
oben links. Hier steht, dass für die Eingangsvektoren 0000 und
0100 das Ausgangssignal jeweils eins ist. Bei der Berechnung
der disjunktiven Normalform ergibt sich für die beiden Zeilen
die Konjunktionen
Die dann zu bildende Disjunktion liefert unter anderem den
Term
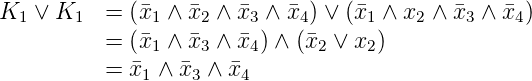 | (2.98) |
Das Beispiel zeigt, dass jedesmal, wenn 2, 4, 8, 16,… Zellen
in einer kompakten Gruppe mit eins belegt sind, dass dann in
der disjunktiven Normalform nur diejenigen Variablen
auftauchen, die sich in der den Zeilen oder Spalten, über
welche die Gruppe geht, nicht verändern.
Aus einem Karnaugh-Diagramm konstruiert man
die Verknüpfungen, indem man alle Felder mit einsen
in möglichst grossen Gruppen zu 2, 4, 8, 16,… Feldern
zusammenfasst und für jede Gruppe die Konjunktion
der unveränderlichen Variablen bildet. Dabei muss
das Diagramm in jeder Richtung als periodisch
Fortgesetzt betrachtet werden. Zum Schluss wird die
entsprechende Disjunktion gebildet.
In Abbildung 2.34 ergeben sich also die Terme
Das Schlussresultat ist dann
[Nächste Seite] [Vorherige Seite] [vorheriges Seitenende]
[Seitenanfang] [Ebene nach oben]
©2002-2017 Ulm
University, Othmar Marti,  Lizenzinformationen
Lizenzinformationen
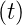 =
=
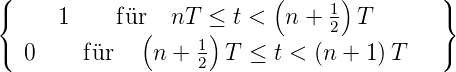 n ∈
Z
n ∈
Z
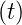 =
=
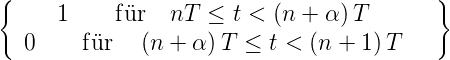 n ∈
Z; 0 ≤α < 1
n ∈
Z; 0 ≤α < 1
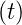 =
= 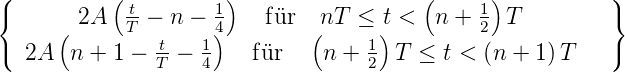 n ∈
Z
n ∈
Z
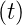 = A
= A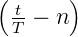 für nT ≤ t <
für nT ≤ t <
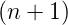 T; n ∈Z
T; n ∈Z 
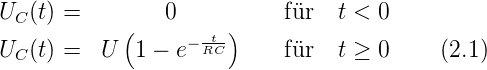
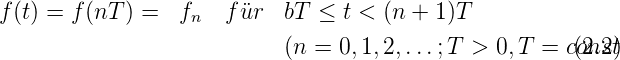
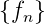 kann in realen Schaltungen gut implementiert werden.
Mathematisch einfacher zu handhaben ist jedoch der
Dirac-Kamm:
kann in realen Schaltungen gut implementiert werden.
Mathematisch einfacher zu handhaben ist jedoch der
Dirac-Kamm:
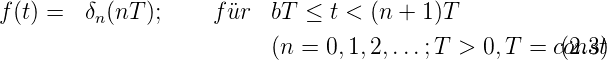
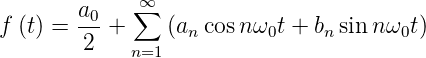
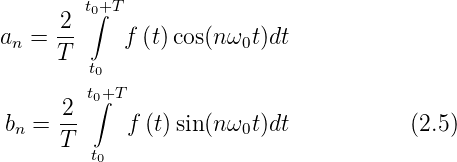
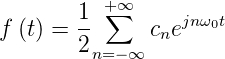
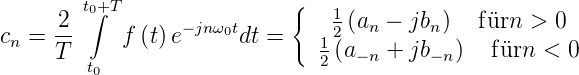
![[f (t) − sm (t)]](phys_elektr47x.png)
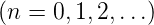 . Dies ist die
. Dies ist die
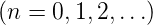 . Dies ist die
. Dies ist die
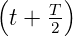
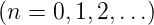 . Dies ist die
. Dies ist die 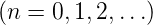 .
.
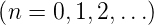 .
.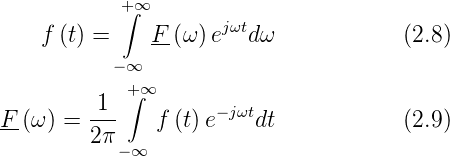
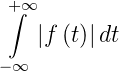
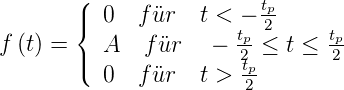
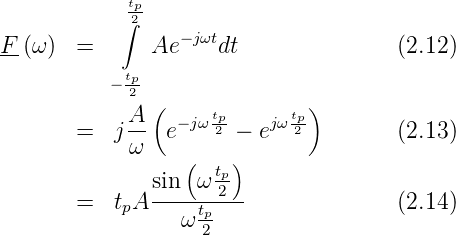
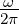
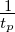 beschränkt.
beschränkt. 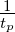 heisst die Bandbreite des
Impulses. Allgemein gilt für Pulse
heisst die Bandbreite des
Impulses. Allgemein gilt für Pulse
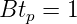
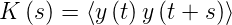
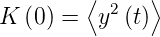
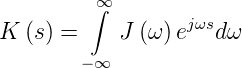
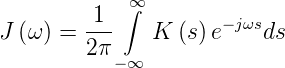
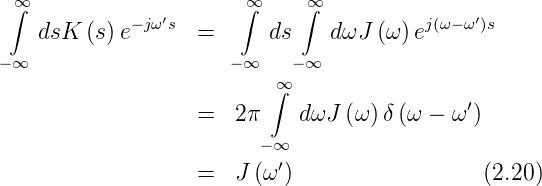
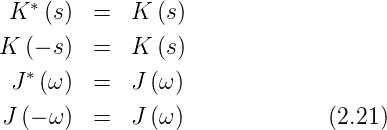
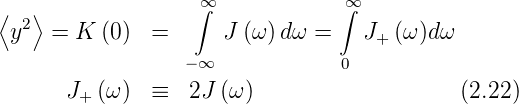
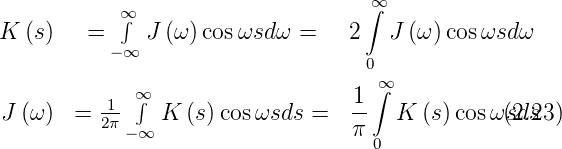
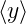 kann
durch das Zeitmittel
kann
durch das Zeitmittel 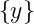 ersetzt werden (Die Definitionen
finden Sie in Reif
ersetzt werden (Die Definitionen
finden Sie in Reif 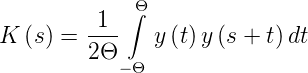
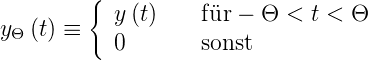
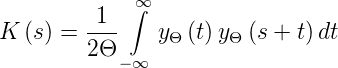
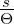 ein, der für
ein, der für 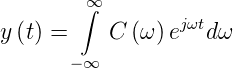
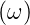 ist die
ist die ![1 ∞∫ ∫∞ ∫∞ ′
K (s) = --- dt dωC (ω) ejωt dω′C (ω′)ejω (s+t)
2Θ −∞ −∞ −∞
∞∫ ∫∞ ∫∞
= -1- dω dω ′C (ω )C (ω′)ejω′s dtej(ω+ ω′)t
2Θ
−∞ −∞ − ∞
1 ∞∫ ∫∞ ′ ′ jω′s ′
= --- dω dω C (ω )C (ω )e [2π δ(ω + ω )]
2Θ −∞ −∞
∞∫
= π- dωC (ω )C (− ω) ejωs
Θ
−∞∞
π- ∫ 2 jωs
= Θ dω |C (ω )|e (2.28)
−∞](phys_elektr78x.png)
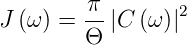
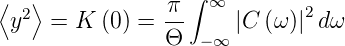
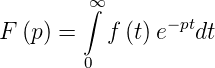
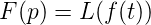
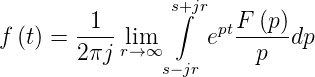
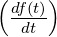
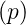
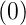
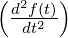
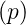
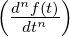
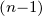
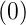
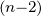
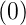
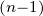
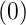
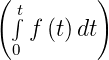
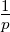
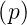

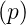 und
und 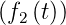
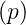 ist,
dann ist auch
ist,
dann ist auch 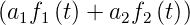
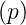
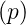
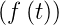
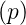 , dann ist
, dann ist
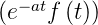
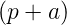
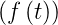
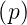 und
und 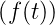
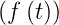
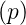 und
und 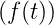
![[ ∫ λ −pt ]
F (p) − 0 e f(t)dt](phys_elektr122x.png)
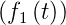
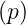 und
und 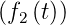
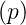 ist, dann ist auch
ist, dann ist auch
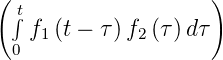
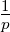
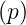
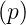
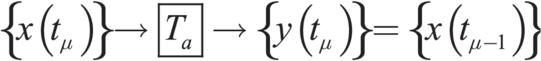
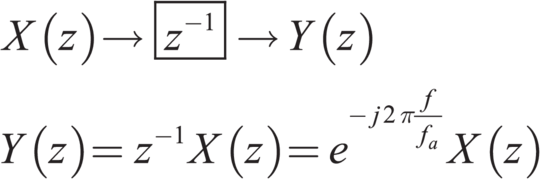
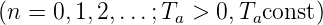 definiert. Die Amplitudenwerte an den diskreten Zeitwerten
sind ebenfalls diskret. Die Folge
definiert. Die Amplitudenwerte an den diskreten Zeitwerten
sind ebenfalls diskret. Die Folge 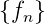 und die an diskreten
Zeitwerten definierte Funktion
und die an diskreten
Zeitwerten definierte Funktion 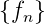 ist definiert
durch
ist definiert
durch
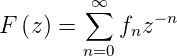
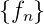 heisst z-transformierbar, wenn die Summe
in Gleichung (
heisst z-transformierbar, wenn die Summe
in Gleichung (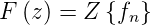
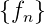 ist die Originalfolge,
ist die Originalfolge, 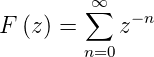
 eine
geometrische Reihe. Sie konvergiert gegen
eine
geometrische Reihe. Sie konvergiert gegen 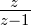 , wenn
, wenn 
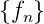 z-transformierbar ist für
alle
z-transformierbar ist für
alle 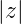
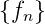 ist
ist 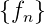 ist dann für
ist dann für 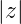
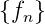 z-transformierbar ist, dann ist
z-transformierbar ist, dann ist 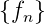 .
.
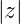
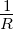 analytisch ist und für
analytisch ist und für 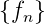 .
.
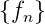 existiert, dann ist
existiert, dann ist
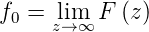
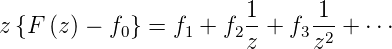
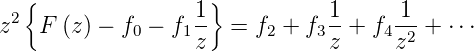
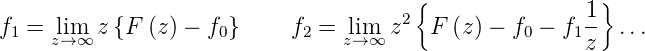
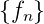
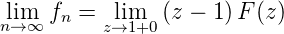
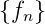 und ihrer z-Transformierten
und ihrer z-Transformierten
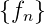
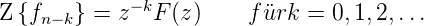
![[ ]
k k∑−1 − ν
Z {fn+k } = z F (z) − fνz f¨urk = 1,2,3,...
ν=0](phys_elektr162x.png)
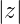
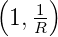 gilt:
gilt:
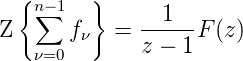
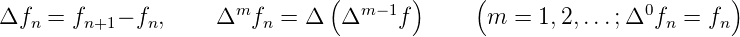
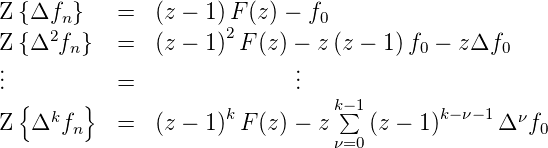
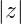
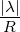 gilt
gilt
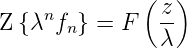
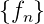 und
und 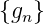 bezeichnet
man
bezeichnet
man
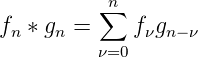
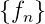
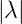
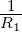 und
und 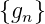
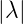
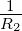 dann ist
dann ist
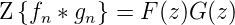
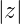
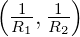 . Dieser
. Dieser 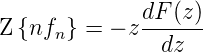
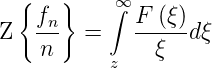
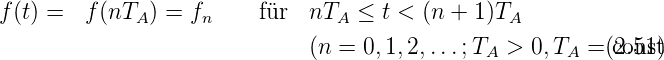
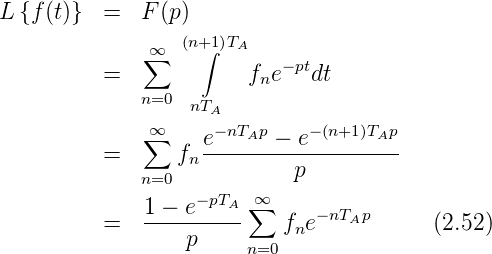
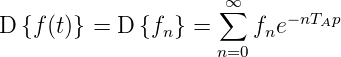
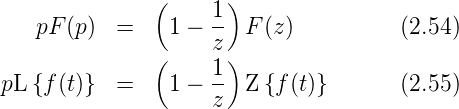
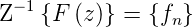
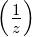 . Es ist
. Es ist

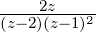 gehörige Folge berechnet
werden.
gehörige Folge berechnet
werden.
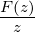 erhält man
erhält man
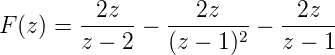
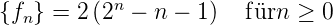

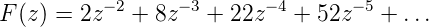
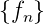 ablesen.
Einen geschlossenen Ausdruck erhält man jedoch
nicht.
ablesen.
Einen geschlossenen Ausdruck erhält man jedoch
nicht.
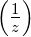
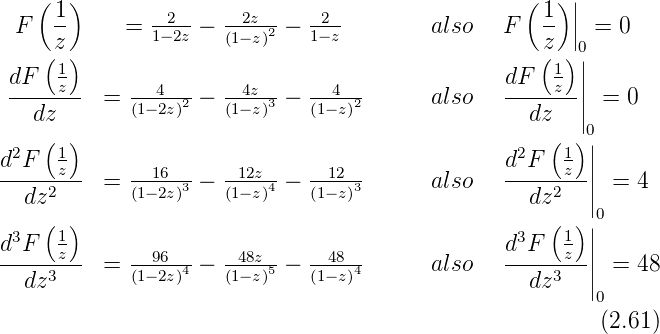
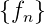 .
.
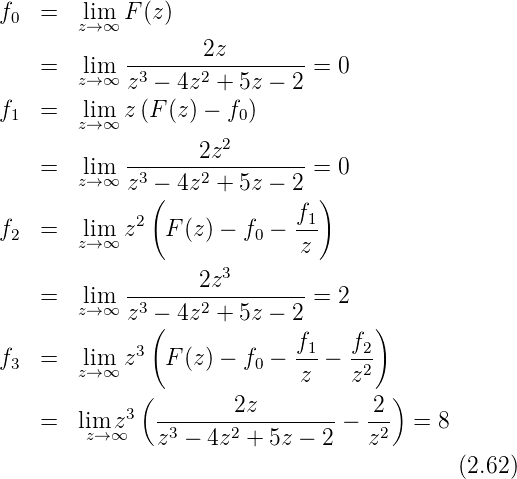
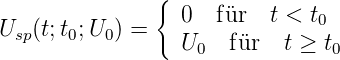
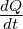
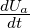 die Differentialgleichung
die Differentialgleichung
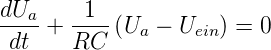
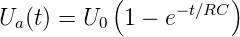
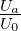 ist die bekannte Exponentialfunktion.
ist die bekannte Exponentialfunktion.
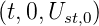 (blau)
und
(blau)
und 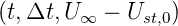 (rot)
(rot)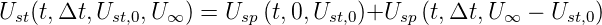
![Ua (t) = U(a (Usp(t,0,Ust,0),t) + Ua (Usp(t,Δt,− Ust,0) ,t)
|| ( 0 ) f¨ur t < 0
{ U 1 − e−t∕RC f¨ur 0 ≤ t < Δt
= || [( sp ) ( )]
( Usp 1 − e−t∕RC − 1 − e− (t−Δt)∕RC f¨ur Δt ≤ t
(
||{ ( 0 ) f¨ur t < 0
= Ust,0 1 − e− t∕RC f¨ur 0 ≤ t < Δt
||( U e−t∕RC (e Δt∕RC − 1) f¨ur Δt ≤ t
( st,0
|| 0 f¨ur t < 0
{ ( −t∕RC)
= || Ust,0 1 − e f¨ur 0 ≤ t < Δt (2.67 )
( Ust,0 ΔRtCe− t∕RC f¨ur Δt ≤ t,Δt → 0](phys_elektr212x.png)
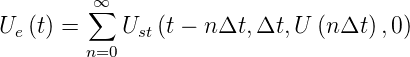
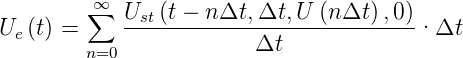
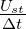 die Diracsche Deltafunktion
die Diracsche Deltafunktion 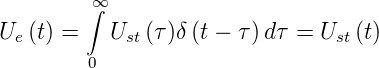
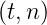 einer einzelnen Stossfunktion erhält
man die Antwort des gesamten Systems
einer einzelnen Stossfunktion erhält
man die Antwort des gesamten Systems
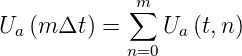
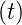
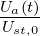 die zeitliche Übertragungsfunktion
eines Einheitsschrittes ist, muss man, um zur Stossantwort
(der Reaktion des Systems auf einen Dirac’schen Deltapuls
die zeitliche Übertragungsfunktion
eines Einheitsschrittes ist, muss man, um zur Stossantwort
(der Reaktion des Systems auf einen Dirac’schen Deltapuls
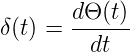
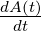 bei einem
bei einem 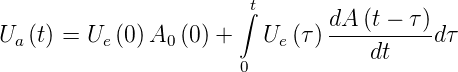
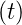
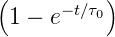 an und berücksichtigt, dass aus Gleichung (
an und berücksichtigt, dass aus Gleichung (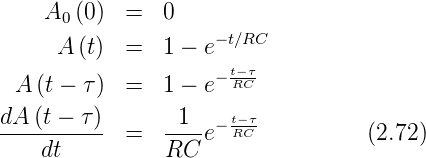
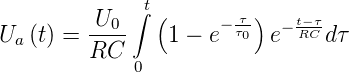
![U0 − t-∫t( τ- ) [ ( t ) − t-]
Ua (t) = --e τ0 e τ0 − 1 dτ = U0 1 − 1 + -- e τ0
τ0 0 τ0](phys_elektr228x.png)
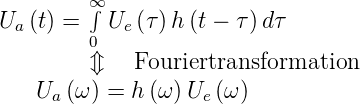

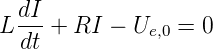
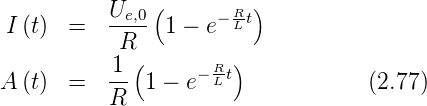
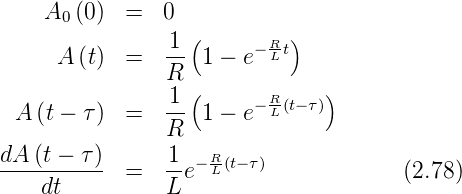
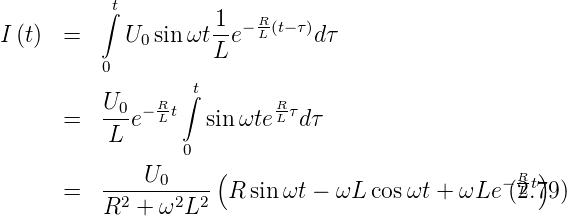
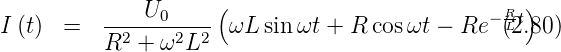
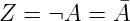

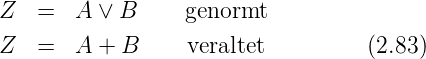
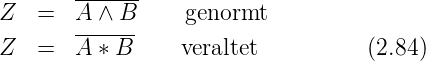
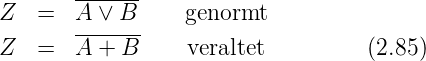
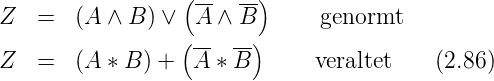
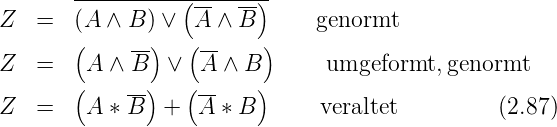
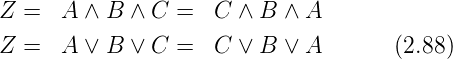
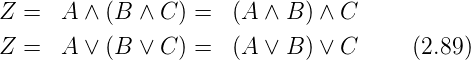
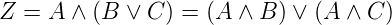
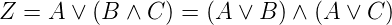
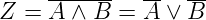
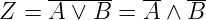
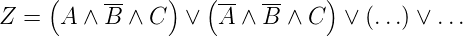
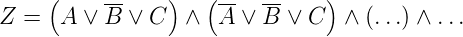
 axterm
axterm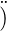 hingeschrieben, wobei
jede Variable mit
hingeschrieben, wobei
jede Variable mit 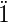 äls
äls 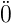 äls
äls 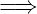
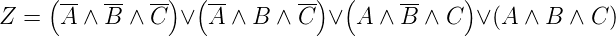
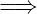
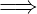
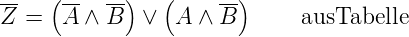
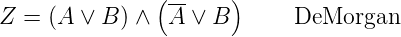
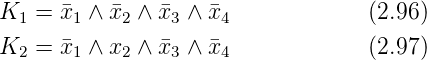
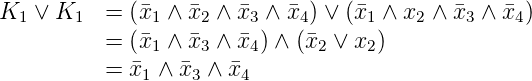
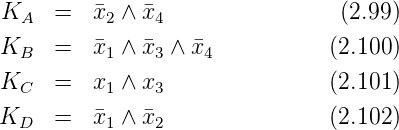
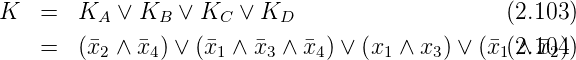
 Lizenzinformationen
Lizenzinformationen