| Dieser Stoff wurde am 6.11.2001 behandelt |
Materialien
| Dieser Stoff wurde am 31.10.2001 behandelt |
![\includegraphics[width=0.7\textwidth]{Bilder/energie-arbeit.eps}](img409.gif)
Arbeit
|
Die Arbeit ![]() im obigen Bild ist
im obigen Bild ist
| (4.104) |
| Einheit der Arbeit oder Energie
|
| Dieser Stoff wurde am 6.11.2001 behandelt |
Materialien:
Folien zur Vorlesung am 06. 11. 2001 PDF
Übungsblatt 4 vom 06. 11. 2001 (HTML oder PDF)
Bei konstanter Beschleunigung und konstanter Masse ist
Der zurückgelegte Weg ist nach Gleichung (3.24)
| (4.105) |
Arbeit:
![$\displaystyle W = F_x \Delta x = m a_x \Delta x = m \left[\frac{v_e^2}{2}-\frac{v_0^2}{2}\right] = \frac{1}{2}m v_e^2-\frac{1}{2}m v_0^2$](img415.gif) |
(4.106) |
Die Beschleunigungsarbeit ändert offensichtlich eine Grösse, die nur von der Masse und von der Geschwindigkeit abhängt.
| Die kinetische Energie
|
| Dieser Stoff wurde am 6.11.2001 behandelt |
Wenn die Kraft nicht konstant ist, so kann die Strecke ![]() in
in ![]() Teilstrecken
Teilstrecken ![]() aufgeteilt
werden.
aufgeteilt
werden.
Die Fläche unter der Kurve ist dann
Der Grenzwert ist das Integral.
Das Integral
ist die Definition der Arbeit |
Beispiel: Fläche unter
![]()
Das Resultat ist
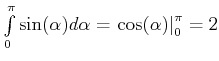 .
.
![\includegraphics[width=0.4\textwidth]{Bilder/arbeit-int-3.eps}](img423.gif)
![\includegraphics[width=0.4\textwidth]{Bilder/arbeit-int-5.eps}](img424.gif)
![\includegraphics[width=0.4\textwidth]{Bilder/arbeit-int-9.eps}](img425.gif)
![\includegraphics[width=0.4\textwidth]{Bilder/arbeit-int-17.eps}](img426.gif)
![\includegraphics[width=0.4\textwidth]{Bilder/arbeit-int-33.eps}](img427.gif)
Fläche unter der Kurve
|
| Dieser Stoff wurde am 6.11.2001 behandelt |
Beispiel: wir spannen eine Feder.
Das Kraftgesetz einer Feder ist
| (4.109) |
Das Minuszeichen bedeutet, dass die Kraft entgegengesetzt zur Auslenkung gerichtet ist. ![]() mit der
Einheit
mit der
Einheit ![]() ist die Federkonstante.
ist die Federkonstante.
Wenn ich als Experimentator die Feder spanne, dann muss ich die Kraft
![]() ausüben.
Die Arbeit, die ich leiste, ist
ausüben.
Die Arbeit, die ich leiste, ist
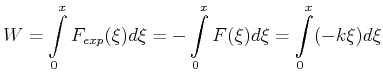 |
(4.110) |
Die Spannarbeit beim Spannen von 0 nach ![]() ist also
ist also
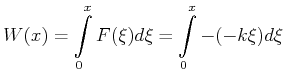 |
(4.111) |
Wir müssen die von uns aufgebrachte Kraft, also die Reaktionskraft zur Federkraft, einsetzen und erhalten richtigerweise positive Kräfte. Die Arbeit, die die Feder verrichtet, ist gegeben aus der durch die Feder erzeugten Kraft und dem Weg: deshalb muss ein Minuszeichen weniger stehen.
| Die Arbeit, die ich an einem System verrichte, wird in dem System als potentielle
Energie gespeichert.
Eine äquivalente Aussage ist: Die potentielle Energie ist die Arbeit gegen die Feldkraft. |
| Dieser Stoff wurde am 6.11.2001 behandelt |
Wir setzten das Kraftgesetz
![]() in die Gleichung (4.40) ein, berücksichtigen, dass wir gegen diese
Kraft arbeiten müssen und erhalten
in die Gleichung (4.40) ein, berücksichtigen, dass wir gegen diese
Kraft arbeiten müssen und erhalten
![$\displaystyle W = \int\limits_{r_1}^{r_2} -(-D r^2) dr = \left.\frac{D}{3} r^3\right\vert _{r_1}^{r_2} = \frac{D}{3}\left[r_2^3-r_1^3\right]$](img437.gif) |
(4.112) |
| Dieser Stoff wurde am 6.11.2001 behandelt |
Wir betrachten einen Massepunkt, der sich auf einer beliebigen Bahn im 3-dimensionalen Raum bewegt. Bei der
Kreisbewegung sahen wir, dass eine senkrecht zur momentanen Geschwindigkeit gerichtete Beschleunigung den
Betrag der Geschwindigkeit nicht ändert. Wir betrachten nun zur Berechnung der Arbeit ![]() die entlang des
Weges wirkende Kraft
die entlang des
Weges wirkende Kraft ![]() .
.
| (4.113) |
wobei ![]() die Länge einer an die Bahnkurve angelegten Sehne ist.
die Länge einer an die Bahnkurve angelegten Sehne ist.
Grenzwert
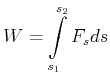 |
(4.114) |
wobei die Länge der Strecke entlang der Bahnkurve mit ![]() gemeint ist.
gemeint ist.
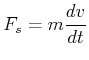 |
(4.115) |
Es gilt, wenn wir die Geschwindigkeit entlang der Bahnkurve
![]() mit der Kettenregel ausrechnen.
mit der Kettenregel ausrechnen. ![]() ist
ein Weglängenelement entlang der Bahnkurve.
ist
ein Weglängenelement entlang der Bahnkurve.
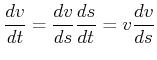 |
(4.116) |
Arbeit
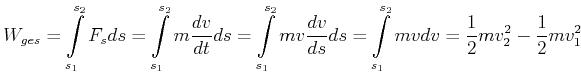 |
(4.117) |
(Siehe Bronstein, Taschenbuch der Mathematik[BSMM00, 189])
Ist ![]() nicht entlang der Bahnkurve
nicht entlang der Bahnkurve ![]() gerichtet, dann muss die Komponente von
gerichtet, dann muss die Komponente von ![]() entlang
entlang
![]() berechnet werden. Wenn der Winkel zwischen der Bahnkurve und der Kraft
berechnet werden. Wenn der Winkel zwischen der Bahnkurve und der Kraft ![]() ist, gilt
ist, gilt
| (4.119) |
Die Funktion, deren Resultat von einem Winkel zwischen zwei Vektoren abhängt, ist das Skalarprodukt.
Definition
| (4.120) |
Rechenregeln
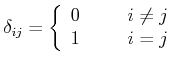
Nun ist die Arbeit entlang eines infinitesimalen Vektors ![]() entlang der Bahnkurve durch
entlang der Bahnkurve durch
| (4.121) |
oder in Integralform
Allgemeine Definition der Arbeit
|
| Dieser Stoff wurde am 6.11.2001 behandelt |
| Die an einem System verrichtete Arbeit führt zu einer Änderung des Energieinhaltes eines Systems. Diese gespeicherte Energie kann bei Bedarf abgegeben werden. Sie heisst deshalb potentielle Energie |
| Potentielle Energien existieren nur, wenn die Kräfte konservativ sind. |
Wenn ein System mit Hilfe seiner potentiellen Energie Arbeit verrichtet, dann nimmt seine potentielle Energie ab.
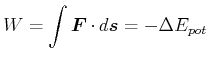 |
(4.123) |
Anders gesagt,
|
Die Lageenergie eines Körpers in Nähe der Erdoberfläche ist (Kraft
![]()
| (4.126) |
oder
| (4.127) |
Auf die Frage nach der Definition der potentiellen Energie mit
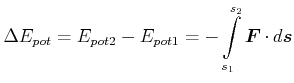
was die richtige Antwort wäre. |
| Dieser Stoff wurde am 7.11.2001 behandelt |
Materialien
Folien zur Vorlesung am 07. 11. 2001 PDF
Beispiel: Feder
Die Federkraft ist ![]() . Deshalb ist die potentielle
Energie der Feder
. Deshalb ist die potentielle
Energie der Feder
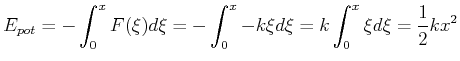 |
(4.128) |
Beispiel: Feder mit progressiver Kennlinie
Sei
![]() . Dann ist
. Dann ist
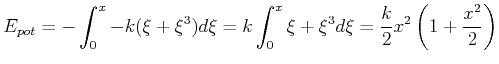 |
(4.129) |
| Dieser Stoff wurde am 7.11.2001 behandelt |
Die potentielle Energie
![]() , die Bahnkurve
, die Bahnkurve
![]() und die Kraft
und die Kraft
![]() , die über die Gleichung (4.57) miteinander
verbunden sind, hängen alle vom Ort ab. In einer Dimension ist klar, dass wenn
, die über die Gleichung (4.57) miteinander
verbunden sind, hängen alle vom Ort ab. In einer Dimension ist klar, dass wenn
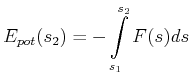 |
(4.130) |
ist, dass dann auch
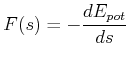 |
(4.131) |
sein muss. In drei Dimensionen kann man sich überlegen, dass die drei Kraftkomponenten entlang der x-, der y- und der z-Achse die Bewegung in Richtung der jeweiligen anderen Achsen nicht beeinflussen (orthogonale Vektoren). Wir hatten bei der Behandlung des schiefen Wurfes gesehen, dass dies so war. Also scheint es angebracht, dass die x Komponente der Kraft nur von der Ableitung der potentiellen Energie nach x abhängt.
| Die Schreibweise
|
Die drei Operationen aus Gleichung (4.65) schreibt man kompakt als Gradientenbildung
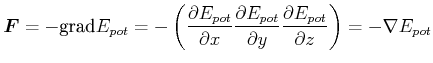 |
(4.133) |
![]() heisst Nabla-Operator und ist eine Kurzschreibweise für die Bildung der drei
partiellen Ableitungen.
heisst Nabla-Operator und ist eine Kurzschreibweise für die Bildung der drei
partiellen Ableitungen.
Bei einer Feder ist die potentielle Energie
![]() . Die Kraft auf das Federende ist gegeben durch
. Die Kraft auf das Federende ist gegeben durch
![]() . Für die Lage
. Für die Lage ![]() ist die Kraft auf das Federende null: dies ist eine Ruhelage. Bei einer
Auslenkung aus der Ruhelage wirkt die Kraft so, dass das Federende gegen die Ruhelage beschleunigt
wird (Minuszeichen in der Kraft).
ist die Kraft auf das Federende null: dies ist eine Ruhelage. Bei einer
Auslenkung aus der Ruhelage wirkt die Kraft so, dass das Federende gegen die Ruhelage beschleunigt
wird (Minuszeichen in der Kraft).
Man unterscheidet die folgenden Gleichgewichte:
Beispiel: Kraft auf zwei Kondensatorplatten (Elektrostatische MEMS)
Ohne Beweis: Zwei Kondensatorplatten der Fläche ![]() im Abstand
im Abstand ![]() geladen auf die Spannung
geladen auf die Spannung ![]() ziehen sich mit
ziehen sich mit
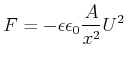 |
(4.134) |
Die potentielle Energie ist dann
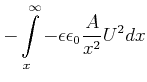 |
|||
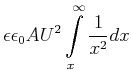 |
|||
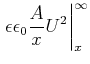 |
|||
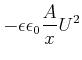 |
(4.135) |
Wenn wir nun eine Blattfeder mit der Aufhängung im Abstand ![]() montieren, so hat diese die
potentielle Energie
montieren, so hat diese die
potentielle Energie
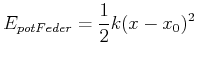 |
(4.136) |
Zusammen ist die potentielle Energie
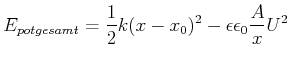 |
(4.137) |
![\includegraphics[width=0.8\textwidth]{potential-feder-kond.eps}](img507.gif)
Diese Funktion ist für verschiedene
|
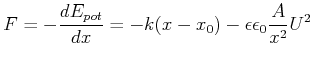 |
(4.138) |
![\includegraphics[width=0.8\textwidth]{kraft-feder-kond.eps}](img510.gif)
Kräfte berechnet für
|
Die Gleichgewichtslage wird mit
![]() berechnet. Uns interessiert die Ruhelage als Funktion
der angelegten Spannung
berechnet. Uns interessiert die Ruhelage als Funktion
der angelegten Spannung ![]() . Die Bestimmungsgleichung ist von dritter Ordnung. Wenn
. Die Bestimmungsgleichung ist von dritter Ordnung. Wenn ![]() ein
Schätzwert ist, dann setzen wir
ein
Schätzwert ist, dann setzen wir
![]() ein und vernachlässigen alle Terme, in denen
ein und vernachlässigen alle Terme, in denen
![]() mit einer höheren als der ersten Potenz vorkommt.
mit einer höheren als der ersten Potenz vorkommt.
| 0 | 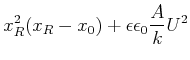 |
||
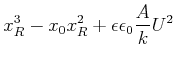 |
|||
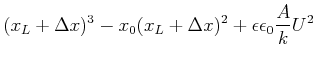 |
|||
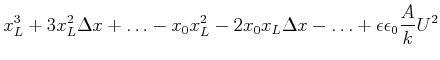 |
(4.139) |
Aufgelöst ergibt sich die Rekursionsformel
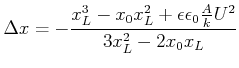 |
(4.140) |
Die erste Näherung erhalten wir, indem wir ![]() setzen.
setzen.
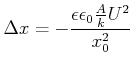 |
(4.141) |
also
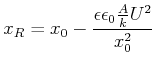 |
(4.142) |
![\includegraphics[width=0.8\textwidth]{kraft-feder-kond-0-2.eps}](img523.gif)
1. (grün, bzw. lila) und 2. (rot bzw blau) Näherungslösung für die Gleichgewichtslage als Funktion der angelegten Spannung. Man beachte, dass die beiden Näherungslösungen nur für kleine Spannungswerte übereinstimmen. Die Diskrepanz rührt daher, dass dieses System eine eingebaute Instabilität besitzt und eine analytische Näherungslösung in deren Nähe versagt.
|
| Dieser Stoff wurde am 7.11.2001 behandelt |
Materialien
Bei einem rein mechanischen konservativen System muss die vom System geleistete in die Änderung der kinetischen Energie gesteckt werden.
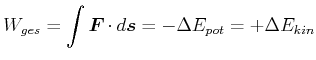 |
(4.143) |
Anders geschrieben
|
Das bedeutet, dass die mechanische Gesamtenergie
| (4.145) |
für konservative Systeme konstant ist. Dies ist der Energieerhaltungssatz der Mechanik.
| Dieser Stoff wurde am 7.11.2001 behandelt |
Bei einem harmonischen Oszillator wird Energie zwischen zwei Reservoirs hin und her verschoben, zwischen der kinetischen Energie und der potentiellen Energie.
![\includegraphics[width=0.8\textwidth]{arbeit-harm-osz.eps}](img527.gif)
Harmonischer Oszillator mit Feder-Masse-System, Federkonstante
|
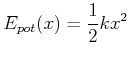 |
(4.146) |
Kinetische Energie mit ![]()
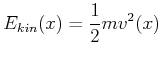 |
(4.147) |
Gesamtenergie
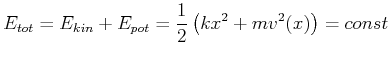 |
(4.148) |
![\includegraphics[width=0.8\textwidth]{arbeit-harm-osz-pot.eps}](img532.gif)
Potentielle Energie (rot) und kinetische Energie (Blau) beim harmonischen Oszillator
|
| Dieser Stoff wurde am 7.11.2001 behandelt |
In einem Potential
![]() gilt
gilt
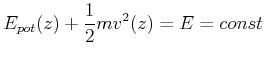 |
(4.149) |
Die Geschwindigkeit ist also gegeben durch
![$\displaystyle v(z) = \sqrt{\frac{2\left[E-E_{pot}(z)\right]}{m}}$](img535.gif) |
(4.150) |
Beispiel:
Im Schwerefeld ist
![]() . Wenn
. Wenn ![]() die Referenzhöhe ist, gilt
die Referenzhöhe ist, gilt
| (4.151) |
![\includegraphics[width=0.8\textwidth]{arbeit-pendel.eps}](img538.gif)
Fadenpendel. Die Höhe ist
|
Der Energieerhaltungssatz der Mechanik besagt, dass
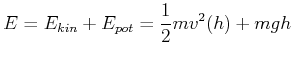 |
(4.152) |
Wenn ![]() die Höhe bei der maximalen Auslenkung ist, dann ist
die Höhe bei der maximalen Auslenkung ist, dann ist
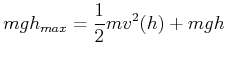 |
(4.153) |
Umgerechnet erhält man
| (4.154) |
| Dieser Stoff wurde am 7.11.2001 behandelt |
Ein zweidimensionales Pendel liegt vor, wenn die potentielle Energie durch
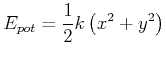 |
(4.155) |
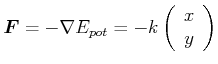 |
(4.156) |
Dieses Pendel zeigt Bewegungen, die in der x-Richtung und in der y-Richtung harmonische Funktionen sind, aber eine Phase beinhalten können.
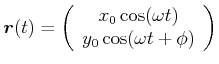 |
(4.157) |
Dies sind Lissajous-Figuren.
Das Potential muss nicht rotationssymmetrisch sein. Wenn wir annehmen, dass die x- und die y-Achse Hauptachsen sind, dann kann das Potential als
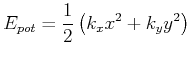 |
(4.158) |
geschrieben werden. Die Kraft ist
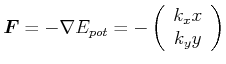 |
(4.159) |
Dieses Pendel zeigt Bewegungen, die in der x-Richtung und in der y-Richtung harmonische Funktionen sind, aber wie vorher auch eine Phase beinhalten können.
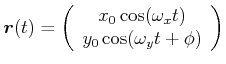 |
(4.160) |
Diese Lissajous-Figuren beschreiben nur dann geschlossene Bahnen, wenn
![]() eine
rationale Zahl ist.
eine
rationale Zahl ist.
| Dieser Stoff wurde am 13.11.2001 behandelt |
Wenn nichtkonservative Kräfte, also Reibungskräfte, vorhanden sind, dann gilt für die Arbeit, die in diese nichtkonservativen Kräfte geht:
| (4.161) |
Die nichtkonservativen Kräfte verringern also die mechanische Energie eines Systems.
| Dieser Stoff wurde am 13.11.2001 behandelt |
Materialien
Folien zur Vorlesung am 13. 11. 2001 PDF
Übungsblatt 5 vom 13. 11. 2001 (HTML oder PDF)
| Die Leistung gibt an, wie schnell Energie (Arbeit) von einem System auf ein zweites übertragen wird. |
| (4.162) |
oder
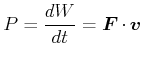 |
(4.163) |
Einheit:
![]() Watt
Watt
Beispiel:
Ein Lastwagen der Masse ![]() fährt einen Berg der Steigung
fährt einen Berg der Steigung ![]() mit der Geschwindigkeit
mit der Geschwindigkeit ![]() hoch.
Was ist die minimal benötigte Leistung?
hoch.
Was ist die minimal benötigte Leistung?
Es gilt:
| (4.164) |
und damit
| (4.165) |
Wenn die Masse des Lastwagens
![]() und seine Geschwindigkeit
und seine Geschwindigkeit ![]() ist, erhalten
wir
ist, erhalten
wir
| Winkel | Steigung [%] | Leistung [kW] |
|---|---|---|
| 0 | 0 | 0 |
| 0.314 | 12,3 | |
| 3.14 | 123 | |
| 6.3 | 246 | |
| 15.8 | 614 |
Umgekehrt, wenn ![]() ist, ist die maximale Geschwindigkeit
ist, ist die maximale Geschwindigkeit
| Winkel | Steigung [%] | Geschwindigkeit [m/s] |
|---|---|---|
| 0.314 | 325 | |
| 3.14 | 32.45 | |
| 6.3 | 16.23 | |
| 15.8 | 6.52 | |
| 32.5 | 3.24 | |
| 100 | 1.30 |
Für einen Personenwagen mit ![]() und
und ![]() gilt
gilt
| Winkel | Steigung [%] | Geschwindigkeit [m/s] |
|---|---|---|
| 0.314 | 1625 | |
| 3.14 | 162.3 | |
| 6.3 | 81.2 | |
| 15.8 | 32.6 | |
| 32.5 | 16.2 | |
| 100 | 6.5 |