| Dieser Stoff wurde am 13.11.2001 behandelt |
| Dieser Stoff wurde am 13.11.2001 behandelt |
Auf einer Geraden ist der Ort des Massenmittelpunktes ![]() ist durch
ist durch
| (4.166) |
Dies ist der mit der Masse gewichtete Mittelwert der Position.
Allgemein für ![]() Massen
Massen
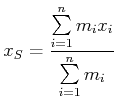 |
(4.167) |
In drei Dimensionen bei ![]() Teilchen
Teilchen
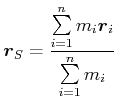 |
(4.168) |
Für kontinuierliche Massenverteilungen
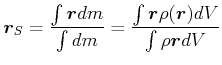 |
(4.169) |
Methode zur Bestimmung des Massenmittelpunktes:
![\includegraphics[width=0.8\textwidth]{Schwerpunkt.eps}](img576.gif)
Ein ebener Testkörper muss mindestens zweimal aufgehängt werden, um den Schwerpunkt
|
| Dieser Stoff wurde am 13.11.2001 behandelt |
Wiederholung: Definition des Schwerpunktes.
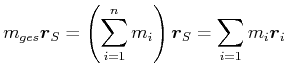 |
(4.170) |
Wir leiten ab und erhalten die Geschwindigkeit (die Masse soll konstant sein)
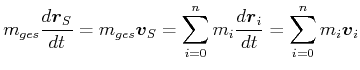 |
(4.171) |
Wir leiten ab und erhalten die Beschleunigung (die Masse soll konstant sein)
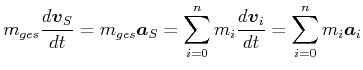 |
(4.172) |
Auf das ![]() -te Massenstück wirken interne Kräfte
-te Massenstück wirken interne Kräfte
![]() und externe Kräfte
und externe Kräfte
![]() . Nach
Newton gilt
. Nach
Newton gilt
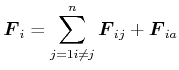 |
(4.173) |
Die beiden letzten Gleichungen kombinieren
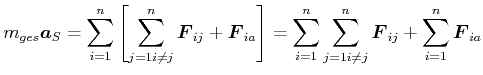 |
(4.174) |
Für die internen Kräfte gilt nach dem 3. Newtonschen Axiom
| (4.175) |
Also wird die Doppelsumme über die internen Kräfte gleich null.
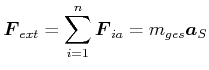 |
(4.176) |
Ein System von Massen bewegt sich so, wie wenn die Summe aller äusseren Kräfte am Massenmittelpunkt angreifen würde.
| Dieser Stoff wurde am 13.11.2001 behandelt |
Materialien
Wir betrachten zwei Teilchen der Masse ![]() , die die Kräfte
, die die Kräfte
![]() und
und
![]() aufeinander
ausüben.
aufeinander
ausüben.
| (4.177) |
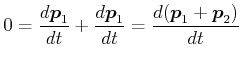 |
(4.178) |
Daraus folgt:
| Wenn keine äusseren Kräfte wirken, gilt, dass
|
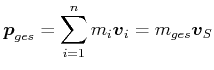 |
(4.179) |
Nun ist nach dem 2. Newtonschen Axiom
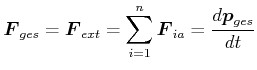 |
(4.180) |
Ohne äussere Kräfte
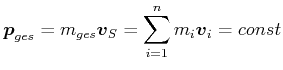 |
(4.181) |
Gesetz der Impulserhaltung
| Dieser Stoff wurde am 13.11.2001 behandelt |
![\includegraphics[width=0.8\textwidth]{impuls-1.eps}](img600.gif)
Kollision zweier Lastwagen mit unterschiedlichen Massen und unterschiedlicher Geschwindigkeit dargestellt im Laborsystem
|
Im Laborsystem sollen die Geschwindigkeiten ![]() und
und ![]() sein. Wenn
sein. Wenn
![]() die Geschwindigkeit des Schwerpunktes ist, ist
die Geschwindigkeit des Schwerpunktes ist, ist
| (4.182) |
![\includegraphics[width=0.8\textwidth]{impuls-2.eps}](img608.gif)
Kollision zweier Lastwagen mit unterschiedlichen Massen und unterschiedlicher Geschwindigkeit dargestellt im Schwerpunktsystem
|
Im Schwerpunktsystem haben beide Lastwagen den gleichen Impuls (der Gesamtimpuls ist ja null). Also gilt dort
| (4.183) |
Wenn wir einen elastischen Stoss annehmen, dann wird
![]() und
und
![]() . Die neuen Geschwindigkeiten sind dann:
. Die neuen Geschwindigkeiten sind dann:
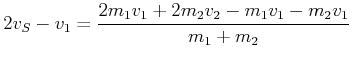 |
|||
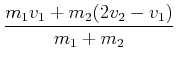 |
|||
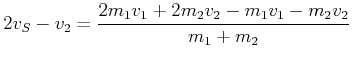 |
|||
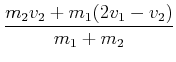 |
(4.184) |
Setzen wir
![]() (Smart),
(Smart),
![]() (z.B. Mercedes-Benz) und
(z.B. Mercedes-Benz) und
![]() und
und
![]() (eine Frontalkollision in der 30-er Zone). Dann erhalten wir
(eine Frontalkollision in der 30-er Zone). Dann erhalten wir
![]() und
und
![]() . Die
gesamte kinetische Energie beider Autos wird also in
das leichtere der beiden übertragen.
. Die
gesamte kinetische Energie beider Autos wird also in
das leichtere der beiden übertragen.
Setzen wir
![]() (Smart),
(Smart),
![]() (z.B. Mercedes-Benz) und
(z.B. Mercedes-Benz) und
![]() und
und
![]() (eine Auffahrkollision auf der Autobahn). Dann erhalten wir
(eine Auffahrkollision auf der Autobahn). Dann erhalten wir
![]() und
und
![]() , eine ziemlich unangenehme Situation für
die Insassen des leichteren Autos.
, eine ziemlich unangenehme Situation für
die Insassen des leichteren Autos.
| Dieser Stoff wurde am 14.11.2001 behandelt |
Materialien
Folien zur Vorlesung am 14. 11. 2001 PDF
Wir betrachten ein System von ![]() Teilchen, jedes mit der Masse
Teilchen, jedes mit der Masse ![]() und der Geschwindigkeit
und der Geschwindigkeit ![]() . Die
Schwerpunktsgeschwindigkeit
. Die
Schwerpunktsgeschwindigkeit
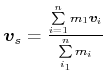 . Jede
Geschwindigkeit wird im Schwerpunktssystem zu
. Jede
Geschwindigkeit wird im Schwerpunktssystem zu
![]() .
.
Die kinetische Energie des Teilchensystems ist
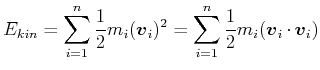 |
(4.185) |
Die Geschwindigkeiten im Schwerpunktssystem eingesetzt ergibt
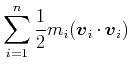 |
|||
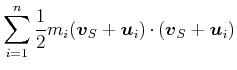 |
|||
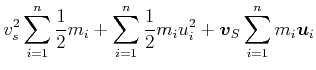 |
(4.186) |
Die letzte Summe ist der Impuls im Schwerpunktsystem, also null. Deshalb ist die gesamte kinetische Energie
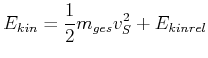 |
(4.187) |
wobei die kinetische Energie der Relativbewegung durch
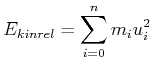 |
(4.188) |
gegeben ist.
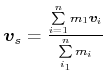 . Jede
Geschwindigkeit wird im Schwerpunktssystem zu
. Jede
Geschwindigkeit wird im Schwerpunktssystem zu
Die kinetische Energie des Teilchensystems ist
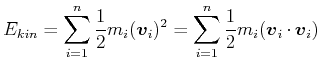 |
(4.189) |
Die Geschwindigkeiten im Schwerpunktssystem eingesetzt ergibt
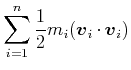 |
|||
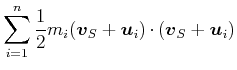 |
|||
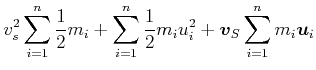 |
(4.190) |
Die letzte Summe ist der Impuls im Schwerpunktsystem, also null. Deshalb ist die gesamte kinetische Energie
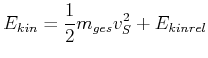 |
(4.191) |
wobei die kinetische Energie der Relativbewegung durch
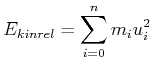 |
(4.192) |
gegeben ist.
| Dieser Stoff wurde am 14.11.2001 behandelt |
Bei jedem Stoss gilt die Impulserhaltung
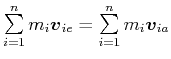 , wobei , wobei
|
| Dieser Stoff wurde am 14.11.2001 behandelt |
Bei einem elastischen Stoss gilt zusätzlich die Energieerhaltung
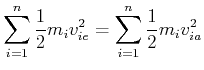 |
(4.193) |
Als Beispiel berechnen wir den elastischen Stoss zweier Massen auf einer Geraden (eine Dimension)
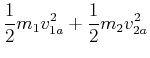 |
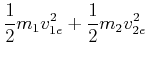 |
(4.194) |
Wir erhalten aus der Energiebedingung
| (4.195) |
oder
Die Impulsbedingung kann analog geschrieben werden
Indem wir die Gleichung (4.125) durch die Gleichung (4.126) teilen ergibt sich
| (4.198) |
oder
| (4.199) |
Dies bedeutet, dass die Relativgeschwindigkeit der beiden Körper wohl das Vorzeichen, nicht aber den Betrag ändert.
| Dieser Stoff wurde am 14.11.2001 behandelt |
Bei einem inelastischen Stoss wird ein Teil der kinetischen Energie der Stosspartner in andere Energieformen umgewandelt. Meistens sind die anderen Energieformen die Wärmeenergie oder die Energie der plastischen Deformation. Denkbar ist aber auch eine Umwandlung in magnetische oder elektrische Energie.
Wir nehmen nun einen vollständig inelastischen Stoss an. Dann vereinen sich die
Stosspartner ![]() und
und ![]() zu einer Masse
zu einer Masse ![]() , die sich mit der Schwepunktsgeschwindigkeit
, die sich mit der Schwepunktsgeschwindigkeit
![]() fortbewegt.
fortbewegt.
| (4.200) |
| Bei jedem Stoss, auch beim inelastischen, gilt die Impulserhaltung |
Impulserhaltung
| (4.201) |
oder
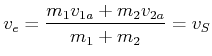 |
(4.202) |
Energiebetrachtung
Vor dem Stoss ist
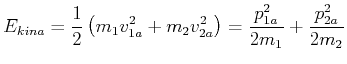 |
(4.203) |
Nach dem Stoss
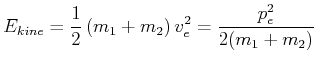 |
(4.204) |
Vergleich
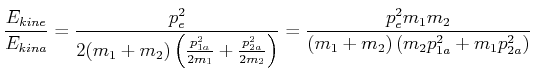 |
(4.205) |
Für den Spezialfall, dass ![]() ergibt sich
ergibt sich
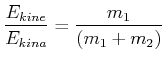 |
(4.206) |
| Dieser Stoff wurde am 14.11.2001 behandelt |
Bei elastischen Stössen von zwei Körpern der gleichen Masse im 2- oder 3-dimensionalen, bei dem ein Körper zu Beginn in Ruhe war, gilt aus der Energieerhaltung:
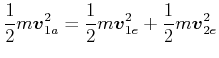 |
(4.207) |
oder
| (4.208) |
Dies ist aber die pythagoräische Gleichung, mit ![]() als Hypotenuse. Damit sind
als Hypotenuse. Damit sind ![]() und
und
![]() Katheten und stehen damit senkrecht aufeinander.
Katheten und stehen damit senkrecht aufeinander.
| Immer dann wenn zwei Teilchen der gleichen Masse, von denen eines am Anfang in Ruhe ist,
elastisch stossen, ist der Winkel zwischen den beiden Endgeschwindigkeiten |
Auch bei unterschiedlichen Massen ist jeder Stoss im Ruhesystem (vor dem Stoss) eines der beiden beteiligten Teilchens in einer Ebene.
![\includegraphics[width=0.8\textwidth]{stoss3d.eps}](img679.gif)
Stoss mit allgemeinen Geschwindigkeiten
|
Im Ruhesystem des 2. Teilchens sind die Geschwindigkeitsvektoren aller Teilchen (![]() ,
,
![]() und
und
![]() ) in einer Ebene. Dies ist einsichtig, wenn man ein Koordinatensystem so legt, dass die x-Achse
parallel zu
) in einer Ebene. Dies ist einsichtig, wenn man ein Koordinatensystem so legt, dass die x-Achse
parallel zu ![]() ist. In diesem Koordinatensystem hat der Gesamtimpuls nur eine x-Komponenten (vor und nach
dem Stoss). Das bedeutet, dass die y- und z-Komponenten der impulse nach dem Stoss für die beiden Teilchen
gegengleich sein müssen. Dann sind die Projektionen von
ist. In diesem Koordinatensystem hat der Gesamtimpuls nur eine x-Komponenten (vor und nach
dem Stoss). Das bedeutet, dass die y- und z-Komponenten der impulse nach dem Stoss für die beiden Teilchen
gegengleich sein müssen. Dann sind die Projektionen von
![]() und
und
![]() kollinear, also liegen
kollinear, also liegen ![]() ,
,
![]() und
und
![]() in einer Ebene. Im ursprünglichen Laborsystem gilt die Aussage nicht mehr!
in einer Ebene. Im ursprünglichen Laborsystem gilt die Aussage nicht mehr!
Im Detail ausgeführt für zwei gleich schwere Teichen geht die Rechnung wie folgt: Zur Betrachtung der
Impulserhaltung legen wir das Koordinatensystem so, dass die x-Achse sich entlang von
![]() befindet. Die
y-Achse soll in der durch
befindet. Die
y-Achse soll in der durch
![]() und
und
![]() aufgespannten Ebene sich befinden. Dann ist die
Impulskomponente in die z-Richtung vorher und nachher null. Die Anfangs-Impulskomponente in die y-Richtung ist
null und bleibt nach dem Stoss null: da die Massen gleich sind gilt auch
aufgespannten Ebene sich befinden. Dann ist die
Impulskomponente in die z-Richtung vorher und nachher null. Die Anfangs-Impulskomponente in die y-Richtung ist
null und bleibt nach dem Stoss null: da die Massen gleich sind gilt auch
| (4.209) |
In x-Richtung erhalten wir
| (4.210) |
Zusammen mit der Energieerhaltung gilt
| (4.211) |
oder
| (4.212) |
Wenn wir ![]() als Parameter annehmen und berücksichtigen, dass
als Parameter annehmen und berücksichtigen, dass
![]() ist, dann ist
ist, dann ist
| (4.213) |
und
| (4.214) |
sowie
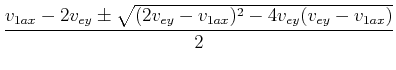 |
|||
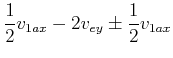 |
(4.215) |
und analog
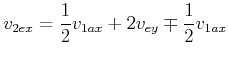 |
(4.216) |
| Dieser Stoff wurde am 14.11.2001 behandelt |
Welche Kräfte wirken bei einem Stoss? Das 2. Newtonsche Axiom sagt, dass
![]() ist. Wir integrieren diese Gleichung über ein Zeitintervall von
ist. Wir integrieren diese Gleichung über ein Zeitintervall von
![]() bis
bis ![]() .
.
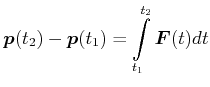 |
(4.217) |
Wenn also eine Kraft (die nicht konstant sein muss) über eine vorgegebene Zeit wirkt, resultiert eine Impulsänderung.
| Mit einem Kraftstoss oder einem Impulsübertrag kann die Wirkung einer sehr kurzzeitigen Kraft beschrieben werden, ohne dass genaue Details über den zeitlichen Verlauf der Kraft bekannt sein müssen. |
Im Detail ausgeführt für zwei gleich schwere Teichen geht die Rechnung wie folgt: Zur Betrachtung der
Impulserhaltung legen wir das Koordinatensystem so, dass die x-Achse sich entlang von
![]() befindet. Die
y-Achse soll in der durch
befindet. Die
y-Achse soll in der durch
![]() und
und
![]() aufgespannten Ebene sich befinden. Dann ist die
Impulskomponente in die z-Richtung vorher und nachher null. Die Anfangs-Impulskomponente in die y-Richtung ist
null und bleibt nach dem Stoss null: da die Massen gleich sind gilt auch
aufgespannten Ebene sich befinden. Dann ist die
Impulskomponente in die z-Richtung vorher und nachher null. Die Anfangs-Impulskomponente in die y-Richtung ist
null und bleibt nach dem Stoss null: da die Massen gleich sind gilt auch
| (4.218) |
In x-Richtung erhalten wir
| (4.219) |
Zusammen mit der Energieerhaltung gilt
| (4.220) |
oder
| (4.221) |
Wenn wir ![]() als Parameter annehmen und berücksichtigen, dass
als Parameter annehmen und berücksichtigen, dass
![]() ist, dann ist
ist, dann ist
| (4.222) |
und
| (4.223) |
sowie
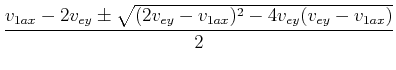 |
|||
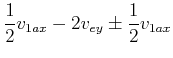 |
(4.224) |
und analog
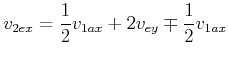 |
(4.225) |
| Dieser Stoff wurde am 14.11.2001 behandelt |
Welche Kräfte wirken bei einem Stoss? Das 2. Newtonsche Axiom sagt, dass
![]() ist. Wir integrieren diese Gleichung über ein Zeitintervall von
ist. Wir integrieren diese Gleichung über ein Zeitintervall von
![]() bis
bis ![]() .
.
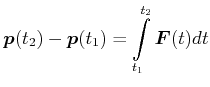 |
(4.226) |
Wenn also eine Kraft (die nicht konstant sein muss) über eine vorgegebene Zeit wirkt, resultiert eine Impulsänderung.
Wirkung eines Kraftstosses
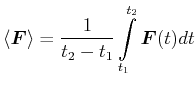 |
(4.227) |
| Dieser Stoff wurde am 14.11.2001 behandelt |
|
[width=0.8]rakete.eps
Geschwindigkeiten und Massen bei einer Rakete
|
Der Gesamtimpuls des Systems bleibt ![]() oder ändert sich um
oder ändert sich um
![]() .
.
Zur Zeit
![]() ist die Masse
ist die Masse ![]() um
um ![]() geändert. Die neue Masse ist also
geändert. Die neue Masse ist also
![]() . Wir wollen zum Schluss unserer Überlegungen auf eine Differentialgleichung
kommen, die wir integrieren können. Dabei nimmt die Masse
. Wir wollen zum Schluss unserer Überlegungen auf eine Differentialgleichung
kommen, die wir integrieren können. Dabei nimmt die Masse ![]() ab. Wir erhalten eine
vorzeichenrichtige Gleichung, wenn wir
ab. Wir erhalten eine
vorzeichenrichtige Gleichung, wenn wir
![]() schreiben. Da die Obergrenze
schreiben. Da die Obergrenze ![]() im
späteren Integral kleiner als die Untergrenze
im
späteren Integral kleiner als die Untergrenze ![]() ist, erhalten wir wieder die ursprüngliche
Ü v_1,a$ befindet. Die
y-Achse soll in der durch
ist, erhalten wir wieder die ursprüngliche
Ü v_1,a$ befindet. Die
y-Achse soll in der durch
![]() und
und
![]() aufgespannten Ebene sich befinden. Dann ist die
Impulskomponente in die z-Richtung vorher und nachher null. Die Anfangs-Impulskomponente in die y-Richtung ist
null und bleibt nach dem Stoss null: da die Massen gleich sind gilt auch
aufgespannten Ebene sich befinden. Dann ist die
Impulskomponente in die z-Richtung vorher und nachher null. Die Anfangs-Impulskomponente in die y-Richtung ist
null und bleibt nach dem Stoss null: da die Massen gleich sind gilt auch
| (4.228) |
In x-Richtung erhalten wir
| (4.229) |
Zusammen mit der Energieerhaltung gilt
| (4.230) |
oder
| (4.231) |
Wenn wir ![]() als Parameter annehmen und berücksichtigen, dass
als Parameter annehmen und berücksichtigen, dass
![]() ist, dann ist
ist, dann ist
| (4.232) |
und
| (4.233) |
sowie
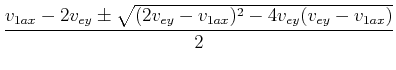 |
|||
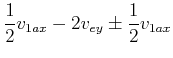 |
(4.234) |
und analog
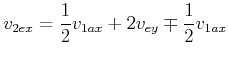 |
(4.235) |
| Dieser Stoff wurde am 14.11.2001 behandelt |
Welche Kräfte wirken bei einem Stoss? Das 2. Newtonsche Axiom sagt, dass
![]() ist. Wir integrieren diese Gleichung über ein Zeitintervall von
ist. Wir integrieren diese Gleichung über ein Zeitintervall von
![]() bis
bis ![]() .
.
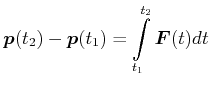 |
(4.236) |
Wenn also eine Kraft (die nicht konstant sein muss) über eine vorgegebene Zeit wirkt, resultiert eine Impulsänderung.
Wirkung eines Kraftstosses
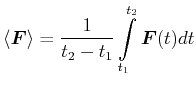 |
(4.237) |
| Dieser Stoff wurde am 14.11.2001 behandelt |
![\includegraphics[width=0.8\textwidth]{rakete.eps}](img720.gif)
Geschwindigkeiten und Massen bei einer Rakete
|
Der Gesamtimpuls des Systems bleibt ![]() oder ändert sich um
oder ändert sich um
![]() .
.
Zur Zeit
![]() ist die Masse
ist die Masse ![]() um
um ![]() geändert. Die neue Masse ist also
geändert. Die neue Masse ist also
![]() . Wir wollen zum Schluss unserer Überlegungen auf eine Differentialgleichung
kommen, die wir integrieren können. Dabei nimmt die Masse
. Wir wollen zum Schluss unserer Überlegungen auf eine Differentialgleichung
kommen, die wir integrieren können. Dabei nimmt die Masse ![]() ab. Wir erhalten eine
vorzeichenrichtige Gleichung, wenn wir
ab. Wir erhalten eine
vorzeichenrichtige Gleichung, wenn wir
![]() schreiben. Da die Obergrenze
schreiben. Da die Obergrenze ![]() im
späteren Integral kleiner als die Untergrenze
im
späteren Integral kleiner als die Untergrenze ![]() ist, erhalten wir wieder die ursprüngliche
berlegung.4
ist, erhalten wir wieder die ursprüngliche
berlegung.4
| (4.238) |
indem die quadratisch kleinen Summanden vernachlässigt werden.
Also bekommt man
| (4.239) |
oder
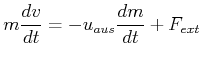 |
(4.240) |
Bei konstanter äusserer Kraft ist5
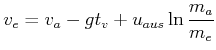 |
(4.241) |