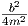J Umrechnung der Losungen des gedampften harmonischen Oszillators

J. Umrechnung der Lösungen des gedämpften harmonischen Oszillators

Die Lösungen für den Fall ω₀² > 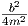-b22-
4m sind

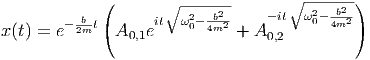( ∘ ------- ∘ ----b2-) -2bmt( it ω20- b4m22- -it ω20-4m2) x(t) = e A0,1e + A 0,2

(J.1)

Mit den Abkürzungen B = b∕(2m) sowie ω′ = ∘ ---------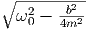
ω2 - -b2--
0 4m2 lautet die Gleichung (J.1)

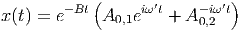( ) x(t) = e-Bt A eiω′t + A -iω′t 0,1 0,2

(J.2)

in der komplexen Schreibweise . Hier sind sowohl der Imaginärteil

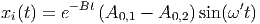xi(t) = e- Bt(A0,1 - A0,2) sin(ω ′t)

wie auch der Realteil

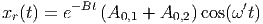xr(t) = e- Bt(A0,1 + A0,2) cos(ω ′t)

Lösungen. Die vollständig geschriebene Lösung ist dann

x(t) = x (t)+x (t) = e-Bt[(A - A ) sin(ω ′t) + (A + A )cos(ω′t)] i r 0,1 0,2 0,1 0,2

(J.3)

Andererseits würde die Lösung mit cos geschrieben

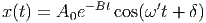x(t) = A e-Btcos(ω ′t + δ) 0

(J.4)

lauten. Hier sind sin und cos in der Phase δ versteckt. Den gemeinsamen Faktor e^-Bt können wir für die Umrechnung weglassen.

x(t) = A0e -Bt[cos(ω′t)cos(δ) - sin(ω ′t)sin(δ)]

(J.5)

Wir vergleichen in den Gleichungen (J.3) und (J.5) die Vorfaktoren von sin und cos und erhalten

A₀ cos(δ)	= A_0,1 + A_0,2	(J.6)
- A₀ sin(δ)	= A_0,1 - A_0,2	(J.7)

Indem wir in Gleichung (J.6) die negierte zweite Zeile durch die erste teilen bekommen wir

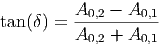A0,2 - A0,1 tan(δ) = ----------- A0,2 + A0,1

(J.8)

Quadrieren wir in Gleichung (J.6) beide Zeilen und addieren sie, erhalten wir

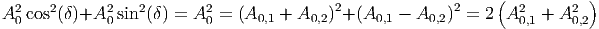2 2 2 2 2 2 2 ( 2 2 ) A 0cos (δ)+A 0sin (δ) = A0 = (A0,1 + A0,2)+ (A0,1 - A0,2) = 2 A 0,1 + A0,2

(J.9)

oder, indem wir die positive Lösung verwenden,

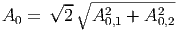√ -∘ ----------- A0 = 2 A20,1 + A20,2

(J.10)