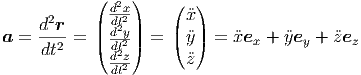

Die Beschleunigung ist in kartesischen Koordinaten
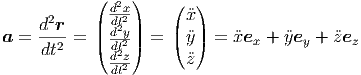 | (G.1) |
Wir verwenden die Beziehungen
| x = | r sin(θ) cos(ϕ) | (G.2) |
| y = | r sin(θ) sin(ϕ) | (G.3) |
| z = | r cos(θ) | (G.4) |
und leiten sie zweimal ab. Wir erhalten aus
| ẋ = | ṙ sin(θ) cos(ϕ) + r cos(θ) cos(ϕ)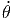 - r sin(θ) sin(ϕ) - r sin(θ) sin(ϕ)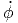 | ||
| ẏ = | ṙ sin(θ) sin(ϕ) + r cos(θ) sin(ϕ)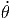 + r sin(θ) cos(ϕ) + r sin(θ) cos(ϕ)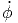 | ||
| ż = | ṙ cos(θ) - r sin(θ)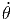 |
die Gleichungen
und
sowie
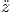 = = | 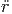 cos(θ) -ṙ sin(θ) cos(θ) -ṙ sin(θ)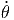 | (G.7) | |
-ṙ sin(θ)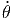 - r cos(θ) - r cos(θ) 2 - r sin(θ) 2 - r sin(θ)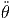 | |||
| = | 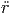 cos(θ) - 2ṙ sin(θ) cos(θ) - 2ṙ sin(θ)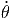 - r cos(θ) - r cos(θ)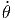 - r sin(θ) - r sin(θ)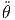 |
Wir setzen in die Gleichung G.1 die Gleichungen G.8, G.9,
G.10, G.5, G.6 und G.7 ein und ordnen nach 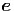 r,
r, 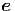 θ und
θ und
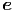 ϕ.
ϕ.
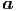 = = | ẍ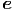 x + ý x + ý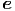 y + y + 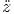 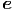 z z | (G.8) | |
| = | ẍ![[sin(θ)cos(ϕ)er + cos(θ)cos(ϕ)e θ - sin(ϕ)eϕ]](td-20152112x.png) | ||
+ ý![[sin (θ )sin (ϕ )er + cos(θ) sin (ϕ )eθ + cos(ϕ )eϕ]](td-20152113x.png) | |||
+ 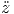 ![[cos(θ)er - sin(θ)eθ]](td-20152115x.png) | |||
| = | ![[¨xsin(θ)cos(ϕ ) + ¨y sin (θ )sin (ϕ ) + z¨cos(θ)]](td-20152116x.png) 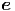 r r | ||
+ ![[¨xcos(θ)cos(ϕ ) + ¨y cos(θ)sin(ϕ) - ¨zsin(θ)]](td-20152118x.png) 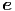 θ θ | |||
+ ![[- ¨x sin (ϕ) + ¨ycos(ϕ)]](td-20152120x.png) 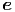 ϕ ϕ |
Der Übersichtlichkeit halber berechnen wir nun die drei
Komponenten 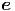 r,
r, 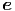 θ und
θ und 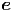 ϕ getrennt. Wir beginnen mit
ϕ getrennt. Wir beginnen mit
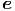 r.
r.
und
| aθ = | ẍ cos(θ) cos(ϕ) + ý cos(θ) sin(ϕ) -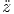 sin(θ) sin(θ) | (G.11) | |
| = | 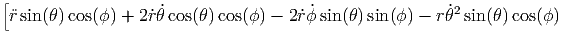 | ||
![]
- 2rϕ˙˙θcos(θ)sin(ϕ) + r¨θcos(θ) cos(ϕ) - r ˙ϕ2sin(θ)cos(ϕ) - r¨ϕ sin (θ )sin (ϕ )](td-20152184x.png) cos(θ) cos(ϕ) cos(θ) cos(ϕ) | |||
+ 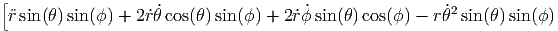 | |||
![2 ]
+2r θ˙ϕ˙cos(θ)cos(ϕ) + r¨θ cos(θ)sin (ϕ ) - r ˙ϕ sin(θ)sin(ϕ) + r¨ϕ sin(θ)cos(ϕ )](td-20152186x.png) cos(θ) sin(ϕ) cos(θ) sin(ϕ) | |||
-![[ ˙ ˙ ¨ ]
¨rcos(θ) - 2˙rθ sin(θ) - rθcos(θ) - rθ sin(θ)](td-20152187x.png) sin(θ) sin(θ) | |||
| = | 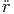 ![[sin (θ )cos(ϕ)cos(θ)cos(ϕ ) + sin(θ)sin(ϕ)cos(θ) sin(ϕ ) - cos(θ) sin(θ)]](td-20152189x.png) | ||
+ 2ṙ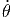 ![[cos(θ)cos(ϕ) cos(θ )cos(ϕ) + cos(θ)sin (ϕ)cos(θ)sin(ϕ) + sin (θ)sin (θ)]](td-20152191x.png) | |||
+ 2ṙ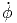 ![[- sin(θ)sin(ϕ) cos(θ )cos(ϕ) + sin(θ) cos(ϕ )cos(θ)sin(ϕ)]](td-20152193x.png) | |||
+ r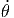 2 2![[- sin(θ) cos(ϕ)cos(θ)cos(ϕ ) - sin(θ)sin(ϕ)cos(θ) sin(ϕ ) + cos(θ)sin(θ)]](td-20152195x.png) | |||
+ 2r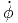 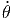 ![[- cos(θ)sin(ϕ) cos(θ)cos(ϕ) + cos(θ)cos(ϕ)cos(θ) sin(ϕ )]](td-20152198x.png) | |||
+ r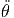 ![[cos(θ)cos(ϕ)cos(θ) cos(ϕ ) + cos(θ) sin(ϕ )cos(θ)sin(ϕ) + sin(θ) sin(θ)]](td-20152200x.png) | |||
+ r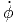 2 2![[- sin (θ)cos(ϕ)cos(θ) cos(ϕ ) - sin(θ)sin(ϕ) cos(θ )sin (ϕ )]](td-20152202x.png) | |||
+ r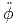 ![[- sin(θ)sin(ϕ)cos(θ)cos(ϕ ) + sin(θ)cos(ϕ) cos(θ)sin (ϕ)]](td-20152204x.png) | |||
| = | 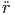 ![[ ]
sin(θ)cos(θ)cos2(ϕ) + sin (θ)cos(θ)sin2(ϕ) - cos(θ)sin (θ)](td-20152206x.png) | ||
+ 2ṙ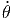 ![[ 2 2 2 2 2 ]
cos (θ)cos (ϕ) + cos (θ)sin (ϕ) + sin (θ)](td-20152208x.png) | |||
+ r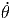 2 2![[ 2 2 ]
- sin (θ)cos(θ)cos (ϕ) - sin (θ)cos(θ)sin (ϕ) + cos(θ)sin (θ )](td-20152210x.png) | |||
+ r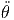 ![[ 2 2 2 2 2 ]
cos (θ)cos (ϕ) + cos (θ)sin (ϕ ) + sin (θ)](td-20152212x.png) | |||
+ r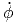 2 2![[ ]
- sin(θ)cos(θ)cos2(ϕ) - sin(θ)cos(θ)sin2(ϕ)](td-20152214x.png) | |||
| = | 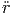 ![[sin (θ )cos(θ) - cos(θ) sin(θ)]](td-20152216x.png) | ||
+ 2ṙ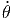 ![[ 2 2 ]
cos (θ) + sin (θ)](td-20152218x.png) | |||
+ r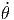 2 2![[- sin(θ) cos(θ) + cos(θ) sin(θ)]](td-20152220x.png) | |||
+ r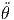 ![[ 2 2 ]
cos (θ) + sin (θ)](td-20152222x.png) | |||
- r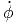 2 2![[sin (θ )cos(θ)]](td-20152224x.png) | |||
| = | 2ṙ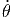 + r + r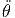 - r sin(θ) cos(θ) - r sin(θ) cos(θ)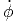 2 2 |
und schliesslich
| aϕ = | -ẍ sin(ϕ) + ý cos(ϕ) | (G.12) | |
| = | -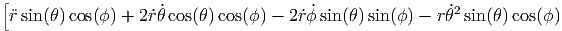 | ||
![]
- 2rϕ˙˙θcos(θ)sin(ϕ) + r¨θ cos(θ )cos(ϕ) - r ˙ϕ2sin(θ)cos(ϕ ) - rϕ¨sin (θ)sin (ϕ)](td-20152229x.png) sin(ϕ) sin(ϕ) | |||
+ 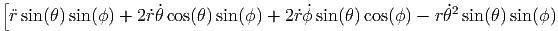 | |||
![2 ]
+2r θ˙˙ϕcos(θ)cos(ϕ ) + rθ¨cos(θ)sin(ϕ) - r ˙ϕ sin(θ)sin(ϕ) + r¨ϕ sin(θ) cos(ϕ)](td-20152231x.png) cos(ϕ) cos(ϕ) | |||
| = | 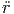 ![[- sin(θ)cos(ϕ) sin(ϕ) + sin(θ)sin(ϕ)cos(ϕ)]](td-20152233x.png) | ||
+ 2ṙ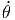 ![[- cos(θ) cos(ϕ )sin (ϕ) + cos(θ )sin (ϕ )cos(ϕ)]](td-20152235x.png) | |||
+ 2ṙ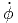 ![[sin(θ)sin(ϕ) sin(ϕ) + sin(θ)cos(ϕ) cos(ϕ )]](td-20152237x.png) | |||
+ r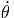 2 2![[sin(θ) cos(ϕ)sin(ϕ) - sin (θ) sin (ϕ )cos(ϕ)]](td-20152239x.png) | |||
+ 2r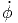 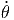 ![[cos(θ)sin(ϕ) sin(ϕ ) + cos(θ)cos(ϕ )cos(ϕ)]](td-20152242x.png) | |||
+ r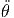 ![[- cos(θ)cos(ϕ) sin(ϕ ) + cos(θ)sin(ϕ) cos(ϕ)]](td-20152244x.png) | |||
+ r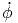 2 2![[sin (θ)cos(ϕ)sin(ϕ) - sin (θ)sin (ϕ)cos(ϕ)]](td-20152246x.png) | |||
+ r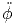 ![[sin(θ)sin(ϕ)sin(ϕ) + sin (θ )cos(ϕ)cos(ϕ)]](td-20152248x.png) | |||
| = | + 2ṙ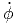 ![[ ]
sin(θ) sin2(ϕ) + sin(θ)cos2(ϕ)](td-20152250x.png) | ||
+ 2r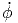 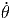 ![[ ]
cos(θ) sin2(ϕ ) + cos(θ)cos2(ϕ )](td-20152253x.png) | |||
+ r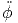 ![[ 2 2 ]
sin(θ)sin (ϕ) + sin (θ) cos (ϕ)](td-20152255x.png) | |||
| = | + 2ṙ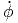 sin(θ) + 2r sin(θ) + 2r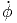 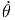 cos(θ) + r cos(θ) + r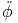 sin(θ) sin(θ) | ||
| = | ![[ ]
r¨ϕ + 2r˙ϕ˙](td-20152260x.png) sin(θ) + 2r sin(θ) + 2r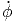 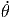 cos(θ) cos(θ) |
Zusammenfassend haben wir
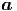 = = | ar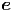 r + aθ r + aθ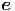 θ + aϕ θ + aϕ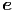 ϕ ϕ | (G.13) | |
| = | ![[ ]
¨r - r˙θ2 - rsin2(θ) ˙ϕ2](td-20152267x.png) 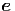 r r | ||
+ ![[ ]
2˙r˙θ + r¨θ - rsin(θ)cos(θ) ˙ϕ2](td-20152269x.png) 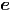 θ θ | |||
+ ![[( ) ]
r¨ϕ + 2˙rϕ˙ sin (θ) + 2r ˙ϕ˙θcos(θ)](td-20152271x.png) 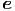 ϕ ϕ |
Wir teilen die Beschleunigung in drei Komponenten auf
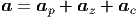 | (G.14) |
Dies ist in der angegebenen Reihenfolge die Parallelbeschleunigung, die den Betrag der Geschwindigkeit erhöht, die Zentripetalbeschleunigung und die Coriolis-Beschleunigung.
Im Einzelnen haben wir
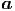 p p | = 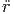 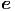 r + r r + r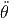 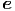 θ + r sin(θ) θ + r sin(θ)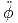 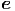 ϕ ϕ | (G.15) |
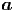 z z | = -r![[ ]
˙θ2 + sin2(θ) ˙ϕ2](td-20152282x.png) 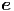 r - r sin(θ) cos(θ) r - r sin(θ) cos(θ)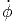 2 2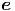 θ
θ | (G.16) |
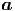 c c | = 2ṙ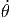 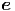 θ + 2 θ + 2![[ ]
r˙sin (θ ) + rθ˙cos(θ)](td-20152289x.png) 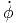 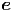 ϕ ϕ | (G.17) |
 Lizenzinformationen
Lizenzinformationen