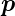 hat. Beim Photon fanden wir aus der relativistischen
Energie-Impuls-Beziehung in Gleichung (4.5)
hat. Beim Photon fanden wir aus der relativistischen
Energie-Impuls-Beziehung in Gleichung (4.5)

Wir haben gesehen, dass Licht sich bei gewissen Experimenten wie dem Fotoeffekt wie ein Teilchen verhält. In diesem Abschnitt wollen wir uns nun fragen, ob auch offensichtliche Teilchen wie das Elektron oder sogar Atome sich wie Wellen verhalten.
Wir wissen, dass jedes Teilchen einen Impuls 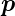 hat. Beim Photon fanden wir aus der relativistischen
Energie-Impuls-Beziehung in Gleichung (4.5)
hat. Beim Photon fanden wir aus der relativistischen
Energie-Impuls-Beziehung in Gleichung (4.5)
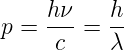
Es lohnt sich, an diesem Punkt ebene Wellen zu betrachten.
Ebene Wellen im Raum haben eine Ausbreitungsrichtung
gegeben durch ihren Wellenvektor 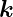 mit
mit
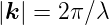 | (4.1) |
(λ ist die Wellenlänge). Sie haben eine Kreisfrequenz ω = 2πν
(ν ist die Frequenz). Wellenvektor und Frequenz sind
über cMedium = λν = ω∕k miteinander verknüpft. Die
momentane Amplitude einer ebenen Welle an einem
beliebigen Raumpunkt 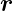 zu einer beliebigen Zeit t ist
zu einer beliebigen Zeit t ist
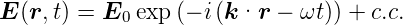 | (4.2) |
+c.c. meint plus das gleiche, aber konjugiert komplex. Physikalisch messbare Grössen sind immer reell.
Wir können mit Gleichung (4.1) Gleichung (4.5) auch schreiben als
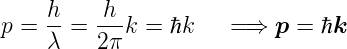 | (4.3) |
Zusammen können wir also einem Teilchen mit einem
Impuls 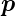 einen Wellenvektor
einen Wellenvektor 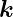 zuschreiben. Man kann sich
jetzt fragen, ob diese Analogie formal ist, oder ob prinzipiell
mit Teilchen die gleichen Interferenzexperimente wie mit
Licht durchgeführt werden können.
zuschreiben. Man kann sich
jetzt fragen, ob diese Analogie formal ist, oder ob prinzipiell
mit Teilchen die gleichen Interferenzexperimente wie mit
Licht durchgeführt werden können.
Dies ist ein fakultativer Abschnitt
| Versuch zur Vorlesung: | |
| Elektronenbeugung: an einer polykristallinen Graphitschicht (Versuchskarte AT-56) | |
Elektronenbeugung ist eine in der Oberflächenphysik[HG91] übliche Methode zur Untersuchung von Probenoberflächen mit periodisch angeordneten Atomen. In den nächsten beiden Abschnitten werden die Beugung niederenergetischer Elektronen sowie die Beugung von Elektronen mit mittlerer Energie besprochen.
Periodische Anordnungen von Atomen werden Netze
genannt, die von zwei Gittervektoren 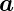 1 und
1 und 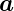 2 aufgespannt
werden. Oberflächennetze sind translationsinvariant. Es gilt
also
2 aufgespannt
werden. Oberflächennetze sind translationsinvariant. Es gilt
also
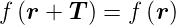 | (4.4) |
mit 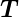 = v
= v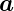 1 + w
1 + w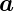 2 wobei v,w ∈ ℤ. f(
2 wobei v,w ∈ ℤ. f(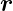 ) ist die
funktionale Darstellung einer beliebigen (auch vektoriellen)
Eigenschaft der Oberfläche. Da die Oberfläche periodisch
translationsinvariant ist, ergibt die Entwicklung von f
) ist die
funktionale Darstellung einer beliebigen (auch vektoriellen)
Eigenschaft der Oberfläche. Da die Oberfläche periodisch
translationsinvariant ist, ergibt die Entwicklung von f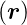 in
eine Fourier-Reihe
in
eine Fourier-Reihe
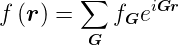 | (4.5) |
Die Summe in Gleichung (4.5) geht über alle reziproken Gittervektoren. Dabei ist
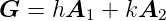 | (4.6) |
wobei h,k ∈ℤ. 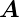 1 und
1 und 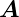 2 sind die erzeugenden Vektoren
diese primitiven Netzes im reziproken Raum, das heisst im
Raum der Raumfrequenzen.
2 sind die erzeugenden Vektoren
diese primitiven Netzes im reziproken Raum, das heisst im
Raum der Raumfrequenzen.
Zwischen dem Netz im realen Raum aufgespannt durch 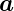 1
und
1
und 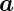 2 und dem Netz im reziproken Raum aufgespannt durch
2 und dem Netz im reziproken Raum aufgespannt durch
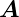 1 und
1 und 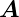 2 muss die Beziehung
2 muss die Beziehung
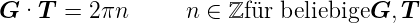 | (4.7) |
gelten. Aus den Beziehungen (4.4) bis (4.7) folgt:
Diese Bedingungen sind erfüllt, wenn 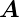 1 und
1 und 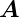 2 wie folgt
konstruiert werden:
2 wie folgt
konstruiert werden:
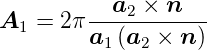 | (4.9) |
und
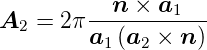 | (4.10) |
Dabei ist 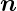 ein beliebiger Vektor senkrecht zum
Oberflächennetz. Abbildung 4.3.1.1 zeigt an einem Beispiel
die Beziehung zwischen den Oberflächennetzen des realen und
des reziproken Raumes.
ein beliebiger Vektor senkrecht zum
Oberflächennetz. Abbildung 4.3.1.1 zeigt an einem Beispiel
die Beziehung zwischen den Oberflächennetzen des realen und
des reziproken Raumes.
__________________________________________________________________________
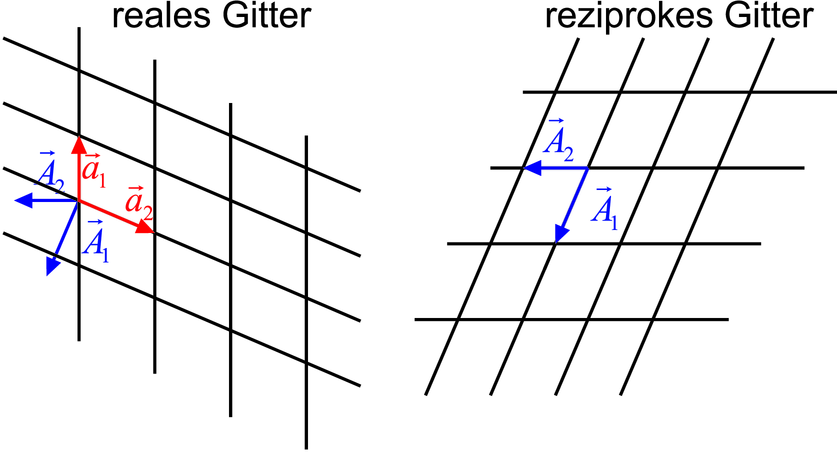
Reales Gitter (links) und reziprokes Gitter (rechts).
_____________________________________________________________________
__________________________________________________________________________
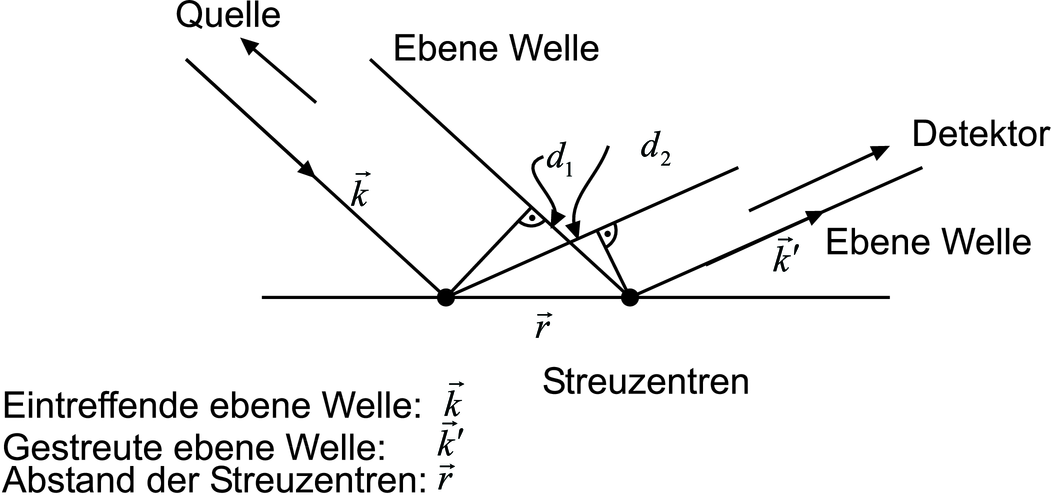
Skizze zur Streuung an Oberflächenatomen
_____________________________________________________________________
Abbildung 4.3.1.2 zeigt die Geometrie der Streuung. Die
einfallende ebene Welle wird mit ihrem Wellenvektor  und
die gestreute ebene Welle mit ihrem Wellenvektor
und
die gestreute ebene Welle mit ihrem Wellenvektor 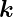 ′
bezeichnet. Der Abstand der Streuzentren sei
′
bezeichnet. Der Abstand der Streuzentren sei 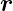 .
.
Die Wegdifferenzen der Wellenzüge zwischen zwei benachbarten Streuzentren sind
Aus dem Wegunterschied berechnet man die Phasendifferenzen für die beiden Wege
Die endgültige Phasendifferenz ist
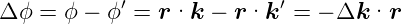 | (4.13) |
mit Δ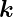 =
= 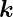 ′−
′−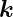 . Für die gestreuten Amplituden am i-ten
Atom gilt ψ′ = ψeiΔ
. Für die gestreuten Amplituden am i-ten
Atom gilt ψ′ = ψeiΔ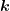 i·
i· .
.
Für die Beträge der Wellenvektoren haben wir
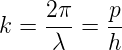 | (4.14) |
Hier ist p der Impuls und mit Gleichung (4.1) λ die Wellenlänge, die für Teilchen die de Broglie–Wellenlänge λ genannt wird.
Für die Streuamplitude eines Netzes mit monoatomarer Basis (also beschreibbar als eine periodische Anordnung von Dirac-δ-Impulsen), erhält man:
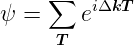 | (4.15) |
mit 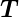 = v·
= v·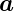 1 + w·
1 + w·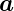 2. Für eine mehratomige Basis erhält
man:
2. Für eine mehratomige Basis erhält
man:
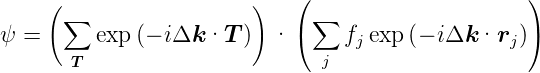 | (4.16) |
fj ist der Streufaktor des j-ten Streuzentrums und 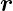 j ist
die Position dieses Streuzentrums in der Einheitszelle.
Der erste Faktor in der Gleichung (4.16) hängt nur vom
Oberflächennetz ab und nicht von der Struktur der
Einheitszelle. Dieser Faktor wird Gittersumme
j ist
die Position dieses Streuzentrums in der Einheitszelle.
Der erste Faktor in der Gleichung (4.16) hängt nur vom
Oberflächennetz ab und nicht von der Struktur der
Einheitszelle. Dieser Faktor wird Gittersumme
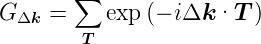 | (4.17) |
genannt. Der zweite Faktor in Gleichung (4.16) ist die geometrische Strukturamplitude
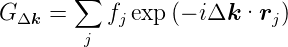 | (4.18) |
Da 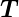 in der Oberfläche liegt, ist
in der Oberfläche liegt, ist
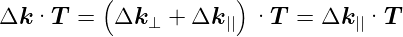 | (4.19) |
Also gilt
Diese Bedingungen heissen Laue-Bedingungen
Bei elastischer Streuung gilt
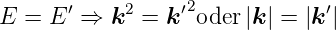 | (4.21) |
__________________________________________________________________________
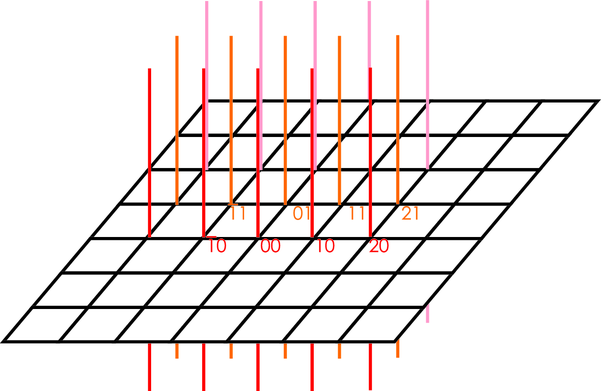
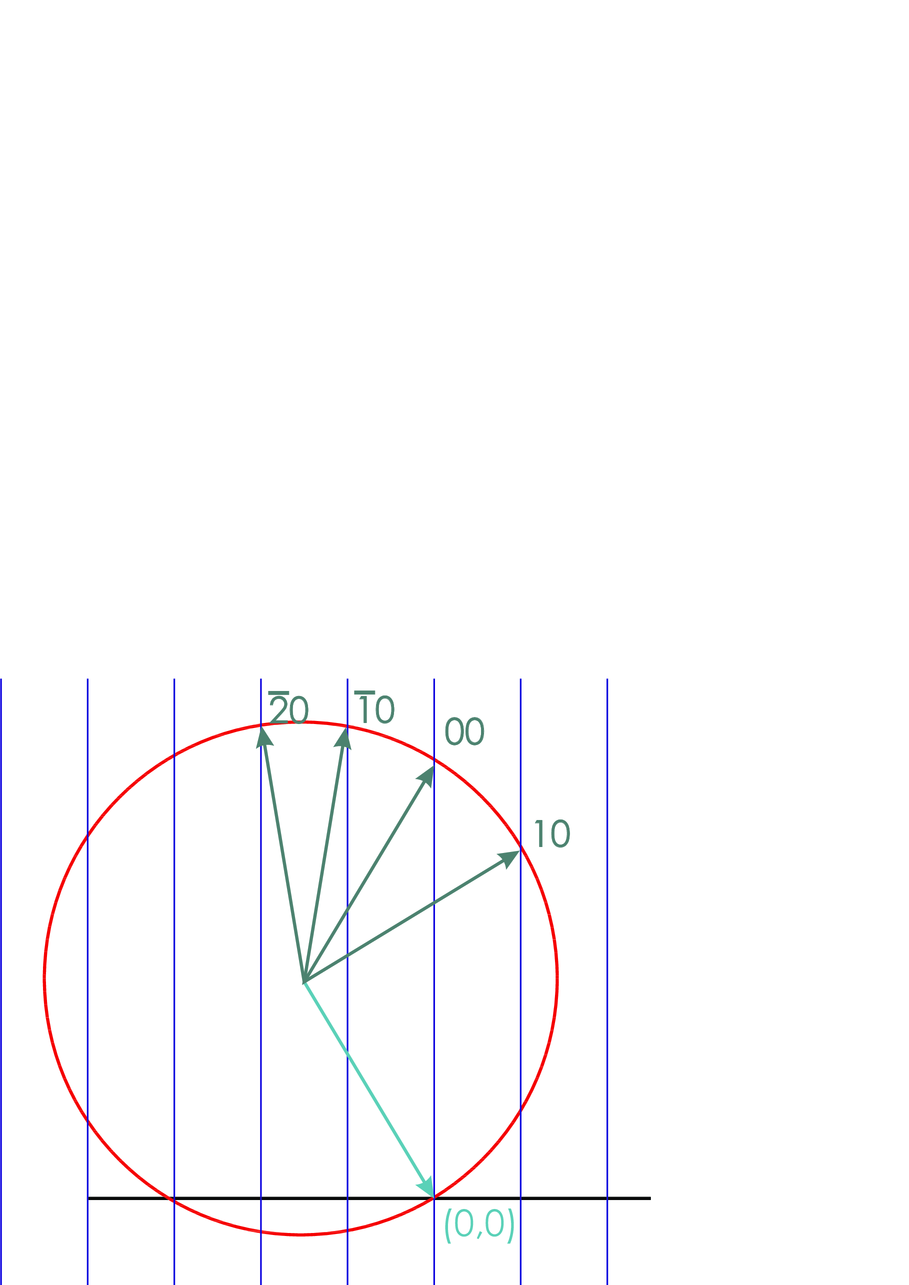
Ewald-Konstruktion für Oberflächennetze. Rechts wird ein Schnitt dargestellt. Oben in der rechten Darstellung sind die Indizes der Reflexe angegeben, unten ist der Ursprung des Koordinatensystems im reziproken Raum.
_____________________________________________________________________
Aus dieser Bedingung kann man die in der Abbildung gezeigte Ewald-Konstruktion für Oberflächennetze ableiten.
Dies ist ein fakultativer Abschnitt
LEED[JSY82] ist die am häufigsten angewandte Methode zur strukturellen Untersuchung periodischer Kristalloberflächen. Die Elektronen werden mit einer bestimmten, möglichst monochromatischen Energie aus einer wohldefinierten Richtung auf die Probe gesandt. Ihre de Broglie-Wellenlänge muss von der gleichen Grössenordnung wie die Gitterperiode an der Kristalloberfläche sein. Wenn man eine Periodizität von 0.1 nm annimmt, so ergibt sich
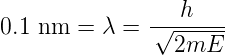 | (4.22) |
Daraus folgt für die Energie
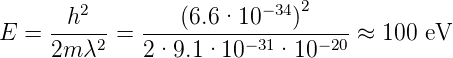 | (4.23) |
__________________________________________________________________________
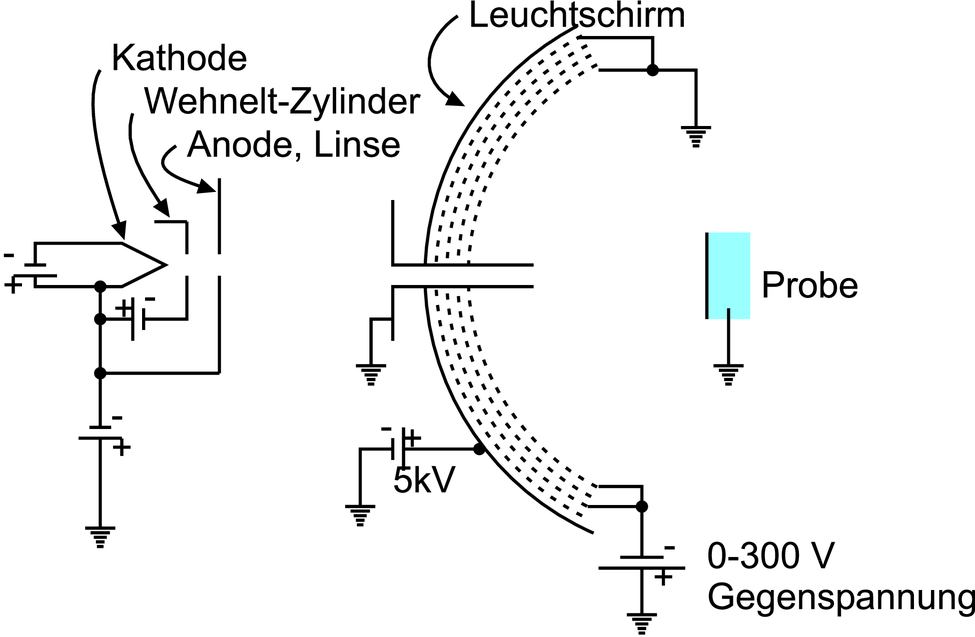
Aufbau eines LEED-Experimentes. Links ist die Elektronenkanone gezeigt. Rechts ist der schematische Aufbau des LEED-Schirms gezeigt.
_____________________________________________________________________
_____________________________________________________________________
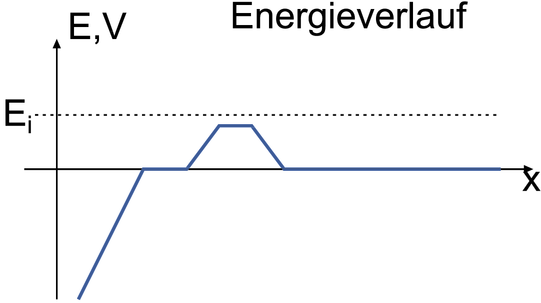
Energieverlauf im LEED-Detektor. Rechts ist der Zwischenraum zwischen der Probe und dem Detektor.
_____________________________________________________________________
Die obere Abbildung zeigt den Aufbau eines LEED. Die Elektronen stammen in der Regel aus einer thermischen Kathode. Nach der Beschleunigungsphase bewegen sich die Elektronen in einem feldfreien Raum bis zur Probe. Die rückgestreuten Elektronen nähern sich dem mit einer phosphoreszierenden Substanz belegten kugelkalottenförmigen Schirm in einem feldfreien Raum. Der Energieverlauf im LEED-Detektor ist schliesslich in der unteren Abbildung gezeigt.
Die Energieunschärfe bei der Emission muss mit der
thermischen Energie bei Raumtemperatur verglichen
werden. Diese ist ΔE ≈kT ≈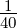 eV. Die Glühemission bei
T = 2000 K ist mit einer Energieunschärfe von ΔE ≈ 0.2 eV
behaftet und damit etwa acht mal grösser als kT bei
Raumtemperatur. Die Energieunschärfe der Feldemission bei
T = 300 K ist schliesslich gleich der thermischen Energie kT,
also ΔE ≈ 0.025 eV.
eV. Die Glühemission bei
T = 2000 K ist mit einer Energieunschärfe von ΔE ≈ 0.2 eV
behaftet und damit etwa acht mal grösser als kT bei
Raumtemperatur. Die Energieunschärfe der Feldemission bei
T = 300 K ist schliesslich gleich der thermischen Energie kT,
also ΔE ≈ 0.025 eV.
__________________________________________________________________________
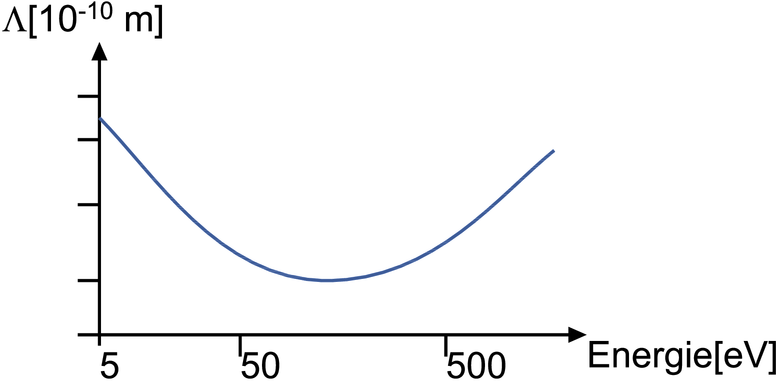
Eindringtiefe der Elektronen als Funktion der Energie
_____________________________________________________________________
Die Abbildung zeigt die Eindringtiefe der Elektronen als Funktion ihrer kinetischen Energie. Die Eindringtiefe ist für Elektronen mit einer Energie von etwa 100 eV minimal. Bei höheren Energien, wie sie zum Beispiel bei der Elektronenmikroskopie vorkommen ist die Eindringtiefe grösser. Sie nimmt über etwa 500 eV monoton mit der kinetischen Energie der Elektronen zu.
Für LEED verwendet man Elektronen mit einer kinetischen Energie von 20 − 500 eV. Die Eindringtiefe der Elektronen ist entsprechend kleiner als einen Nanometer.
__________________________________________________________________________
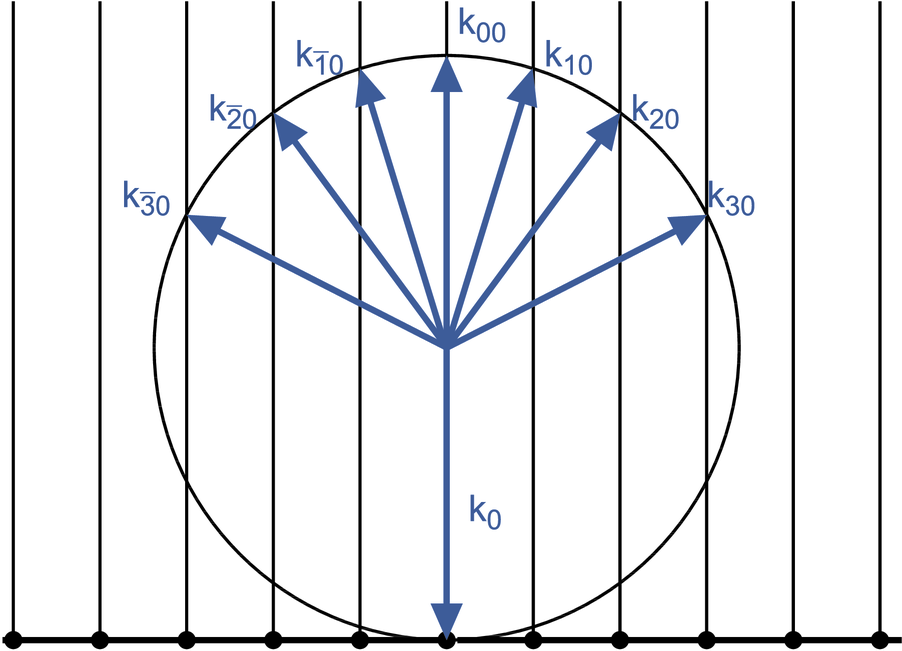
Ewaldkonstruktion für LEED
_____________________________________________________________________
Das durch die Wechselwirkung der langsamen Elektronen mit der Probe entstehende Beugungsbild kann mit Hilfe der Ewald-Konstruktion wie in der Abbildung gezeigt interpretiert werden.
Zwischen der periodischen Struktur der Probenoberfläche oder einer eventuell vorhandenen Überstruktur und der Überstruktur im reziproken Raum besteht folgender Zusammenhang:
Hier ist (siehe Physikalische Elektronik und Messtechnik) S die die Struktur der Oberfläche charakterisierende Matrix. Nach der Gleichung (4.25) kennt man mit Srez auch S.
Damit Beugungseffekte in der Abbildung mit Elektronen beobachtet werden können, muss die Kohärenzlänge der Elektronen grösser als die maximal möglichen Wegunterschiede sein. Wie bei Licht müssen zwei Arten von Kohärenz unterschieden werden.
__________________________________________________________________________
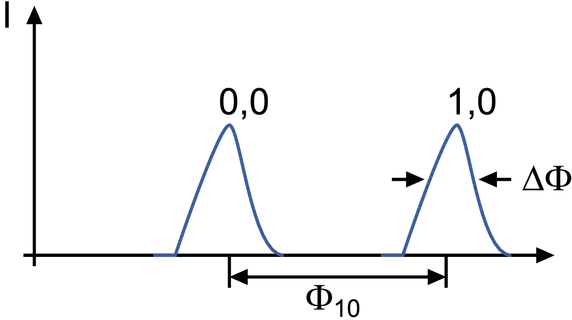
Beugungsmuster und Definitionen zur Transferweite.
_____________________________________________________________________
Aus Abbildung 4.3.1.3 kann die Transferweite t definiert werden.
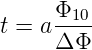 | (4.26) |
Mit ihr bezeichnet man die Breite des Elektronenstrahls, die bei perfekter Quelle und perfekter Abbildung die gleiche Breite der Leuchtflächen bewirkt wie der Elektronenstrahl im realen LEED.
Setzt man Zahlen ein, erhält man t ≈ 10 nm. Da Elektronen eine sehr kleine Kohärenzlänge haben und da sie als Fermionen nicht im gleichen Quantenzustand sein können,1 kann jedes Elektron nur mit sich selber interferieren.
__________________________________________________________________________

Schematische Skizze eines LEED-Bildes von Cu(110) (gezeichnet nach [JSY82]). Dies ist eine FCC-Struktur. Die Messung wurde bei 36 eV aufgenommen.
_____________________________________________________________________
_____________________________________________________________________

Schematische Skizze eines LEED-Bildes von Ni (111) bei einer Primärenergie von 205 eV(gezeichnet nach [JSY82]).
_____________________________________________________________________
__________________________________________________________________________
_____________________________________________________________________
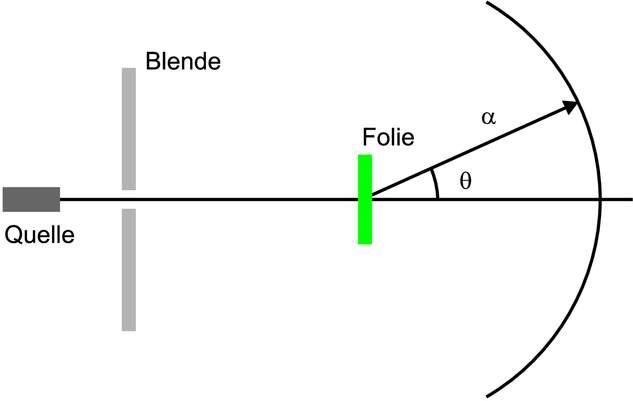
Bei der Rutherford-Streuung nach Abbildung 4.3.2 wird eine Quelle von α-Teilchen durch eine Lochblende auf eine Probe gesendet. Die Lochblende kollimiert den Strahl und verringert den Raumwinkel der Quelle. Die Probe wird in der Physik oft auch mit dem Wort Target bezeichnet. Die Fluchtlinie zur Quelle (gegeben durch die Quelle und die Blende) ist die z-Achse. Die gestreuten Teilchen bewegen sich im Winkel 𝜃 auf den Detektor zu. Bei ungeordneten Targets wie Gasen oder polykristallinen Materialien hängt der Streuwinkel 𝜃 nicht vom Azimut ab.
Rutherford konnte aus der Analyse seiner Streudaten schliessen, dass fast die ganze Masse eines Atoms in einem sehr kleinen, positiv geladenen Kern konzentriert ist und dass die negativ geladene sehr leichte Hülle die Grösse der Atome ausmacht. Bei Stössen ist die Wechselwirkung abhängig vom Massenverhältnis der Stosspartner. Die schweren α-Teilchen werden durch die Elektronen kaum gestört, so wie ein Vogel bei einer Kollision mit einem Auto den Weg des Autos kaum beeinflusst.
__________________________________________________________________________
_____________________________________________________________________
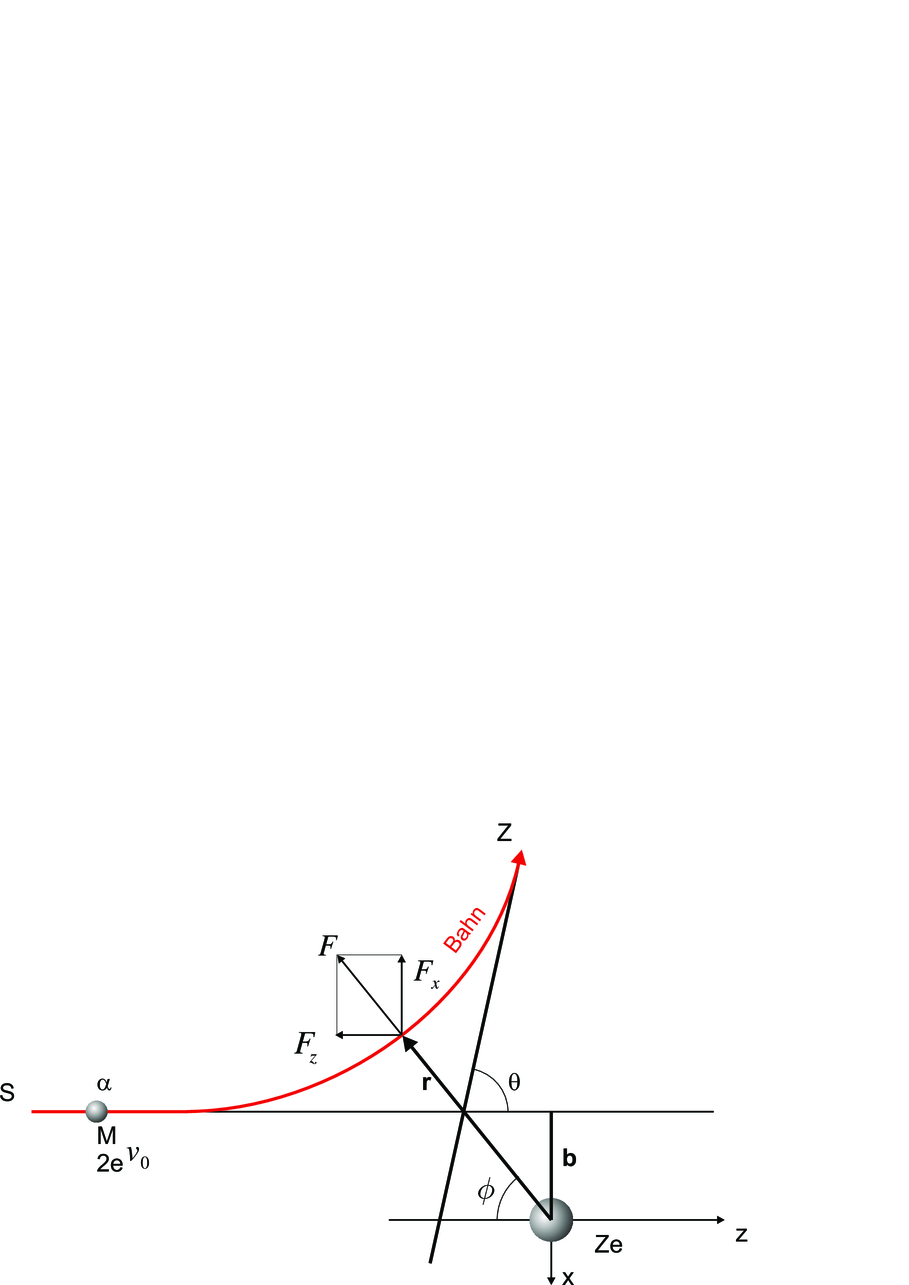
Zur Berechnung der Rutherford-Streuung verwenden wir ein
Koordinatensystem wie in der Abbildung 4.3.2. Das α-Teilchen
kommt aus 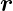 S =
S = 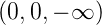 mit der Ursprungsgeschwindigkeit
mit der Ursprungsgeschwindigkeit
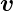 0 =
0 = 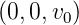 . Nach der Streuung bewegt sich das α-Teilchen
nach
. Nach der Streuung bewegt sich das α-Teilchen
nach 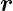 Z = lim a→∞
Z = lim a→∞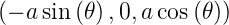 mit der
Geschwindigkeit
mit der
Geschwindigkeit 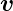 z =
z = 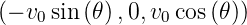 . Zwischen
dem Kern und dem α-Teilchen wirkt eine Zentralkraft, die
Coulombkraft
. Zwischen
dem Kern und dem α-Teilchen wirkt eine Zentralkraft, die
Coulombkraft
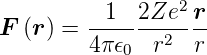 | (4.27) |
Die Kraft 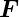 kann in zwei Komponenten entlang der
x-Achse und der z-Achse aufgespalten werden.
kann in zwei Komponenten entlang der
x-Achse und der z-Achse aufgespalten werden.
Die Coulomb-Kraft 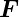 ist eine Zentralkraft. Deshalb ist der
Drehimpuls
ist eine Zentralkraft. Deshalb ist der
Drehimpuls 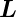 bezüglich des Koordinatenursprungs erhalten.
Als Zentralkraft ist die Coulomb-Kraft auch eine konservative
Kraft. Das heisst dass
bezüglich des Koordinatenursprungs erhalten.
Als Zentralkraft ist die Coulomb-Kraft auch eine konservative
Kraft. Das heisst dass 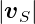 =
= 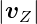 ist, da im Unendlichen die
Coulombkraft verschwindet.
ist, da im Unendlichen die
Coulombkraft verschwindet.
Der Anfangsdrehimpuls sowie der Drehimpuls an einem beliebigen Ort
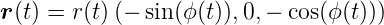
sind
Also
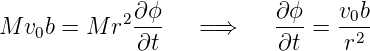 | (4.30) |
Weiter müssen wir die Newtonsche Bewegungsgleichung lösen. Die Newtonsche Bewegungsgleichung in die x-Richtung hat den Vorteil, dass die Anfangsbedingung vx,0 = 0 ist. Unter Verwendung von Gleichung (4.30) bekommen wir
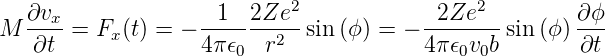 | (4.31) |
Diese Gleichung kann direkt integriert werden
Der Endwinkel ist ϕZ = π −𝜃. Die Endgeschwindigkeit ist vx,Z = −v0 sin(ϕZ) = −v0 sin(𝜃). Also lautet Gleichung (4.32)
Unter Verwendung von 1 + cos(𝜃) = sin(𝜃) cot(𝜃∕2) erhalten wir
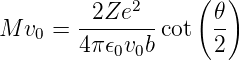 | (4.34) |
Der Stossparameter b hängt vom Streuwinkel 𝜃 ab
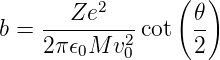 | (4.35) |
Wenn man annimmt, dass im kreisförmigen Intervall zwischen b und b + db eine gewisse Anzahl Teilchen eingestrahlt werden, dann treffen diese im Winkelsegment zwischen 𝜃 und 𝜃 + d𝜃 auf. Also benötigen wir auch
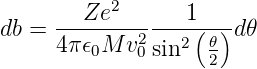 | (4.36) |
das Problem ist zylindersymmetrisch bezüglicher der z-Achse. Zwischen b und b + db ist die Fläche
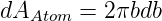 | (4.37) |
Das Target ist in der Regel eine Folie mit der Dicke DFolie, der bestrahlten Fläche AFolie und der Zahlendichte der Atome N.
Insgesamt streuen Ngesamt = DFolieAFolieN Teilchen. Die gesamte Fläche, die zur Streuung in den Bereich d𝜃 um 𝜃 beiträgt, ist
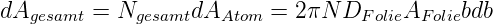 | (4.38) |
Wenn nun n α-Teilchen eintreffen, dann werden
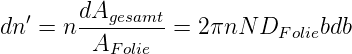 | (4.39) |
Teilchen gestreut.
An der Detektorfläche berechnen wir den bestrahlten Raumwinkel
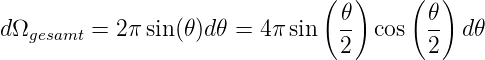 | (4.40) |
Der Detektor misst nur einen kleinen Raumwinkelbereich dΩ, da er in der Regel nur schmal ist. In den Detektor gelangen dann
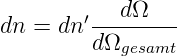 | (4.41) |
Teilchen. Alles zusammengefügt erhält man
die Streuformel von Rutherford
|
__________________________________________________________________________
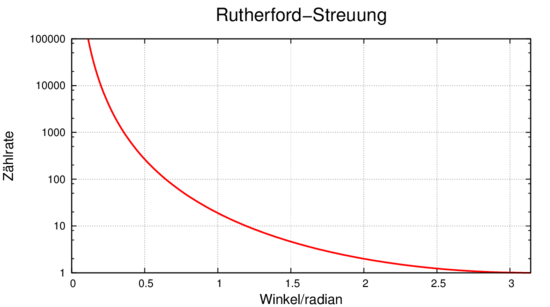
_____________________________________________________________________
Abbildung 4.3.2 zeigt die mit der Gleichung (4.42) berechnete Streukurve.
__________________________________________________________________________
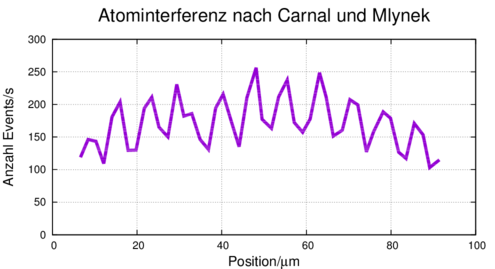
Zweistrahlinterferenz von Atomen (gezeichnet nach [CM91]).
_____________________________________________________________________
Die Experimente von Carnal und Mlynek [CM91] im Jahre 1991 haben gezeigt, dass auch kompliziertere Objekte wie Atome Interferenzerscheinungen zeigen. Neuerere Experimente haben gezeigt, dass auch mehratomige Moleküle wie ein Wellenpaket interferieren. Ausser dass die Wellenlänge enorm klein ist, gibt es nichts, was den Wellencharakter eines Fussballs verbieten würde.
 Lizenzinformationen
Lizenzinformationen