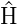 (Lösungen der Schrödingergleichung)
oder jedes anderen Operators nicht die räumliche
Verteilung eines Teilchens. Nach Niels Bohr und der
Kopenhagener Interpretation befindet sich ein Teilchen mit
Wahrscheinlichkeitsdichte
(Lösungen der Schrödingergleichung)
oder jedes anderen Operators nicht die räumliche
Verteilung eines Teilchens. Nach Niels Bohr und der
Kopenhagener Interpretation befindet sich ein Teilchen mit
Wahrscheinlichkeitsdichte 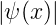 2 = ψ∗(x)ψ(x) am Ort
x.
2 = ψ∗(x)ψ(x) am Ort
x.

Wie oben ausgeführt, beschreiben die Eigenfunktionen
des Operators 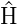 (Lösungen der Schrödingergleichung)
oder jedes anderen Operators nicht die räumliche
Verteilung eines Teilchens. Nach Niels Bohr und der
Kopenhagener Interpretation befindet sich ein Teilchen mit
Wahrscheinlichkeitsdichte
(Lösungen der Schrödingergleichung)
oder jedes anderen Operators nicht die räumliche
Verteilung eines Teilchens. Nach Niels Bohr und der
Kopenhagener Interpretation befindet sich ein Teilchen mit
Wahrscheinlichkeitsdichte 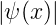 2 = ψ∗(x)ψ(x) am Ort
x.
2 = ψ∗(x)ψ(x) am Ort
x.
Wenn der Impuls px = ℏkx entlang der x-Achse eines Teilchens nicht scharf definiert ist, das heisst wenn das Teilchen nicht durch eine ebene Welle (unendlich ausgedehnt!) beschrieben wird, hat der Impuls des Teilchens eine Streuung Δpx∕2. Mit einer Fouriertransformation kann man den Ort ausrechnen, wenn bekannt ist, dass das Teilchen sich im Impulsraum zwischen px − Δpx∕2 ≤px ≤px + Δpx∕2 aufhält. Wir erwarten ein Resulat analog zur Beugung einer ebenen Welle an einem Spalt, also eine sinc(z) = sin(z)∕z-Funktion.
Wir betrachten nur den Ortsanteil der Wellenfunktion
ψ(x,t) = ψ0 exp 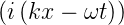 .
.
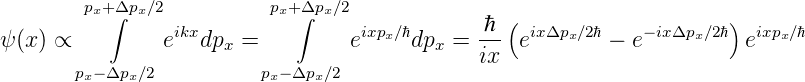 | (5.1) |
dieses Resultat kann umgeformt werden
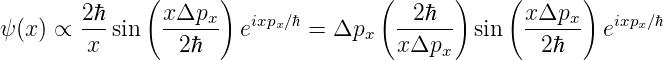 | (5.2) |
Die Amplitude der Ortswellenfunktion ψ(x) ist abhängig von der Position, also also keine echte ebene Welle. Die Amplitude proportional zu:
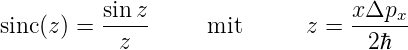
Die erste Nullstelle von sin(z)∕z liegt bei z = π. Wenn wir
annehmen, dass 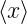 = 0 ist, können wir schreiben
= 0 ist, können wir schreiben
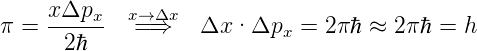 | (5.3) |
Das Produkt ΔxΔpx = h zeigt die realisierbare Genauigkeit der simultanen Orts- und Impulsbestimmung. Ein Wellenpaket mit einer Gauss’schen Einhüllenden ist in Abbildung 5.5.1 gezeigt. Bei diesem Wellenpakte kann gezeigt werden, dass das Produkt ΔxΔpx den minimal möglichen Wert annimmt.
__________________________________________________________________________
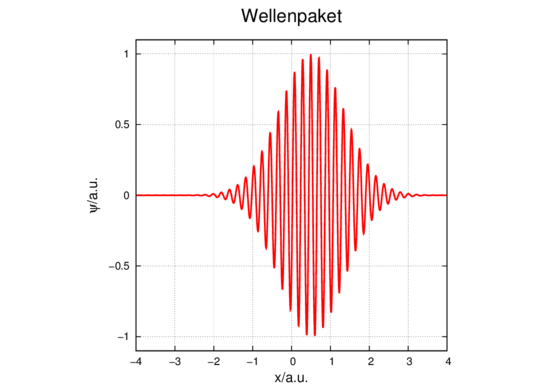
Wellenpaket.
_____________________________________________________________________
 Lizenzinformationen
Lizenzinformationen