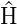 hat die Form
hat die Form

Wenn die potentielle Energie V (x) eine quadratisch von x
abhängt ist die Bewegung des Teilchens beschränkt und
analog zum Fall eines klassischen harmonischen Oszillators.
Der Operator 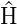 hat die Form
hat die Form
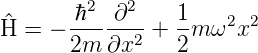 | (5.1) |
mit der potentiellen Energie
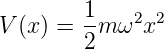 | (5.2) |
Die Lösungen der Schrödingergleichung sind stationär und haben, dem Separationsansatz entsprechend, die Form
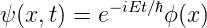 | (5.3) |
Damit können wir die zeitunabhängige Schrödingergleichung verwenden
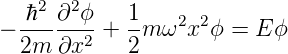 | (5.4) |
__________________________________________________________________________
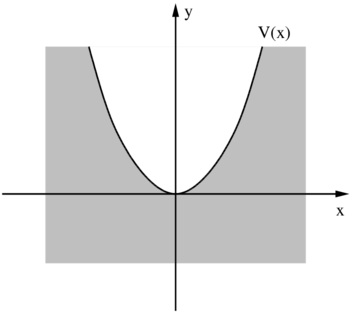
Mögliche Energiefunktion eines harmonischen Oszillators.
_____________________________________________________________________
Wir definieren drei Parameter und ersetzen die Variable x durch u
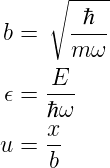 | (5.5) |
Die Gleichung 5.4 lautet dann (siehe auch [CH67, p. 280, Kap. 5, §10])
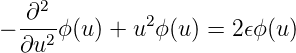 | (5.6) |
Um die Eigenfunktionen ϕn und die Eigenwerte 𝜖n (oder En) zu finden, definieren wir die folgenden Operatoren:
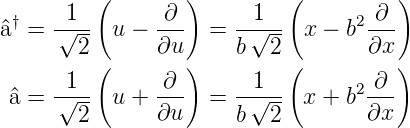 | (5.7) |
Die Operatoren 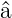 † und
† und 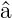 sind nicht hermitisch (also nicht
selbstadjungiert). Sie sind aber adjungiert zueinander.
Deshalb kann man mit
sind nicht hermitisch (also nicht
selbstadjungiert). Sie sind aber adjungiert zueinander.
Deshalb kann man mit
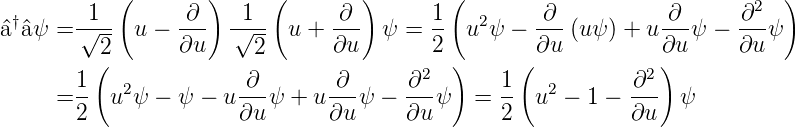
formal schreiben
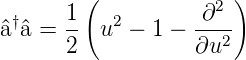 | (5.8) |
Also wird Gleichung (5.6)
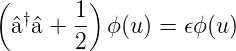 | (5.9) |
Die Hamiltonoperator kann mit den Operatoren 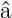 und
und 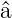 †
umgeschrieben werden
†
umgeschrieben werden
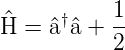 | (5.10) |
Der Kommutator der Operatoren 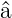 und
und 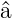 † hat den
Wert
† hat den
Wert
![[ †] † †
^a,^a = ^a^a − ^a ^a = 1](ap-2015481x.png) | (5.11) |
Die Eigenschaften des Kommutators zeigen, dass
![[^a,^a ] = 0](ap-2015482x.png) | (5.12) |
und
![[ ]
^a †,^a † = 0](ap-2015483x.png) | (5.13) |
Wir wollen nun untersuchen, wie die Gleichung (5.9) sich
ändert, wenn wir sie von links mit 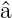 oder
oder 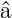 † multiplizieren.
Wir schreiben Gleichung (5.9) um
† multiplizieren.
Wir schreiben Gleichung (5.9) um
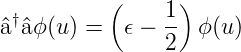 | (5.14) |
Multiplizieren wir Gleichung (5.14) von links mit 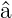 und
verwenden Gleichung (5.11) erhalten wir
und
verwenden Gleichung (5.11) erhalten wir
Wenn ϕ(u) eine Lösung der Gleichung (5.14)
mit dem Eigenwert (𝜖 − 1∕2) ist, ist 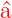 ϕ(u) eine
Lösung der gleichen Gleichung (5.14), aber mit dem
Eigenwert ϕ(u) eine
Lösung der gleichen Gleichung (5.14), aber mit dem
Eigenwert 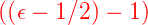 . Der Operator . Der Operator 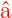 erniedrigt
den Eigenwert um 1. Er wird Absteigeoperator oder
Vernichtungsoperator genannt. erniedrigt
den Eigenwert um 1. Er wird Absteigeoperator oder
Vernichtungsoperator genannt. |
Multiplizieren wir Gleichung (5.14) von links mit 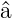 † und
verwenden Gleichung (5.11) erhalten wir
† und
verwenden Gleichung (5.11) erhalten wir
Wenn ϕ(u) eine Lösung der Gleichung (5.14)
mit dem Eigenwert (𝜖 − 1∕2) ist, ist 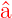 †ϕ(u) eine
Lösung der gleichen Gleichung (5.14), aber mit dem
Eigenwert †ϕ(u) eine
Lösung der gleichen Gleichung (5.14), aber mit dem
Eigenwert 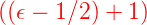 . Der Operator . Der Operator 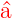 † erhöht den
Eigenwert um 1. Er wird Aufsteigeoperator oder
Erzeugungsoperator genannt. † erhöht den
Eigenwert um 1. Er wird Aufsteigeoperator oder
Erzeugungsoperator genannt. |
Wenn wir eine endliche Energieskala haben, muss es eine
kleinste Energie und damit auch einen kleinsten Eigenwert
geben. Das heisst, es muss eine Ortswellenfunktion ϕ0(u)
geben, auf die angewandt der Vernichtungsoperator 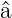 eine
Nullfunktion ergibt.
eine
Nullfunktion ergibt.
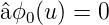 | (5.17) |
Wir verwenden die Definition von 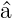 und erhalten
und erhalten
Die Konstante C ergibt sich aus der Normalisierungsbedingung
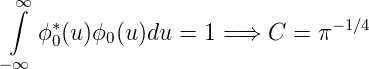
Die normierte Wellenfunktion des Grundzustandes des harmonischen Oszillators in den Koordinaten u und x ist
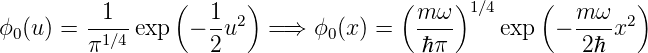 | (5.19) |
Ausgehend von ϕ0(u) können wir nun durch die wiederholte
Anwendung von 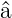 † auf ϕ
0(u) alle Lösungen generieren.
† auf ϕ
0(u) alle Lösungen generieren.
Die ersten nicht normierten Funktionen sind
Mit der Normalisierungsbedingung, dass das Integral über der Wahrscheinlichkeitsdichte gleich eins sein soll, bekommen wir
Aus 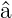 ϕ0(u) = 0 und Gleichung (5.14) folgt, dass
ϕ0(u) = 0 und Gleichung (5.14) folgt, dass
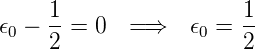 | (5.22) |
Allgemein ist also
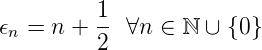 | (5.23) |
Wir erinnern uns an die Substitutionen in Gleichung (5.5). Deshalb sind die
Energieeigenwerte des harmonischen Oszillators
|
Die gleichabständigen Energieeigenwerte des harmonischen Oszillators sind für diesen charakteristisch. Der kleinste Energieeigenwert E0 hat den Wert ℏω∕2. Es ist nicht möglich, einen harmonischen Oszillator in Ruhe zu haben. Die minimale Energie E0 ist die Nullpunktsenergie. Sie bewirkt, dass harmonische Oszillatoren immer Energie enthalten, egal wie tief die Temperatur sinkt. Das heisst, die Boltzmannverteilung aus der klassischen Thermodynamik gilt nicht mehr.
Die Lösungen von Gleichung (5.14) können mit Hermite-Polynomen ausgedrückt werden.[CH67, p. 77, Kap. 2, §9, 4.]
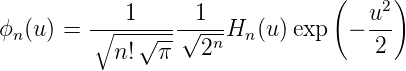 | (5.25) |
mit
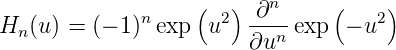 | (5.26) |
Die ersten (nicht normierbaren) Hermite-Polynome sind
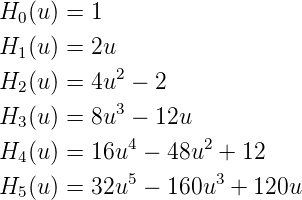 | (5.27) |
Die Normierungsbedingung ist erfüllt, da
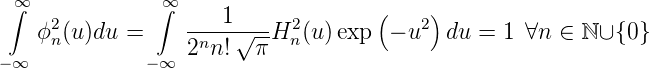
ist. Hermite-Polynome haben die folgenden Eigenschaften
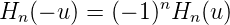 | (5.28) |
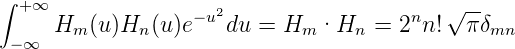 | (5.29) |
__________________________________________________________________________
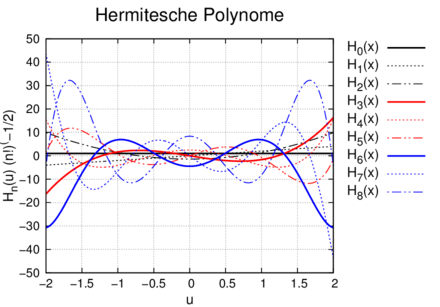
Die ersten acht Hermite-Polynome.
_____________________________________________________________________
Wenn wir die Substitutionen aus Gleichung (5.5) rückgängig machen, erhalten wir
Die Normierungsbedingung ist
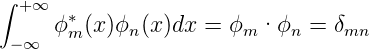 | (5.32) |
__________________________________________________________________________
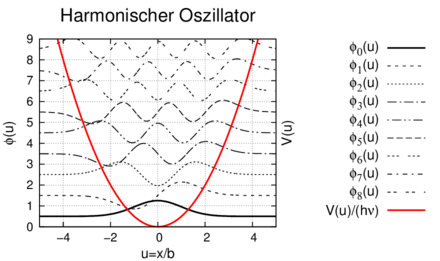
Wellenfunktionen des harmonischen Oszillators
_____________________________________________________________________
_____________________________________________________________________
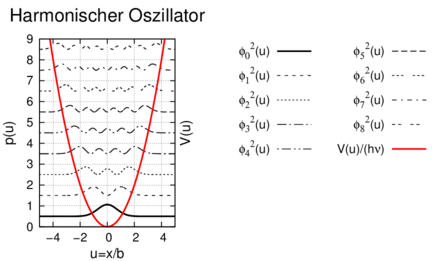
Wahrscheinlichkeitsdichte der Wellenfunktionen des harmonischen Oszillators
_____________________________________________________________________
__________________________________________________________________________
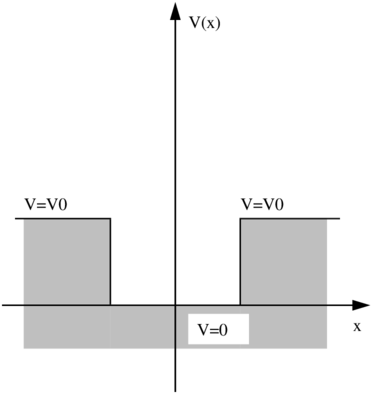
Potentialtopf.
_____________________________________________________________________
Der Fall eines Teilchens in einem endlichen Potentialtopf ist etwas komplizierter als der Fall des unendlichen. Die Wellenfunktion verschwindet nicht am Rand des Topfes. Wir müssen zwei Fälle betrachten: wenn die Energie höher als die Potentialwälle ist, also E > V 0 und wenn sie kleiner ist. Im ersten Falle haben wir zum Beispiel eine von links einlaufende Welle, die sich an den Diskontinuitäten des Potentials reflektiert. Diese Lösung müsste aus der Lösung des Potentialwalls ablesbar sein. Im zweiten Falle haben wir lokalisierte Wellenfunktionen.
______________________________________________________________________________________________________
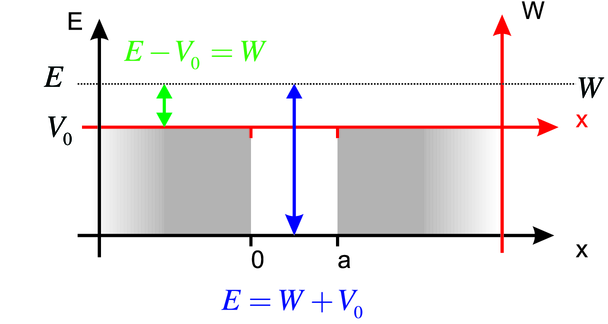
Transformation einer Potentialschwelle in einen Potentialtopf
_____________________________________________________________________
Die Lösungen sind in Gleichung (5.4) angegeben und werden hier nochmals wiederholt.
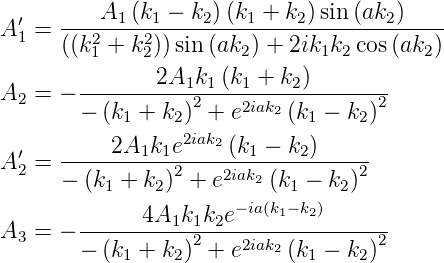
A1 stellt die einfallende Welle dar. der Wert ist frei wählbar. Die Energiewerte müssen aus Gleichung (5.5)
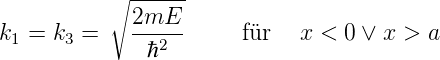 |
und Gleichung (5.6)
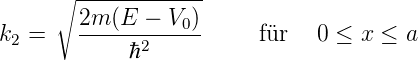 |
werden umskaliert mit E → E −V 0 ausserhalb und E −V 0 →E im Topf. Wir erhalten
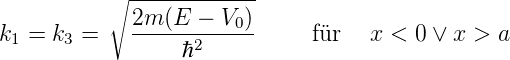 | (5.33) |
und
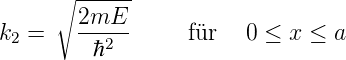 | (5.34) |
Daraus folgen die Transmissions- und Reflexionskoeffizienten T und R
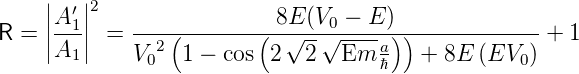 | (5.35) |
und
Die Transmissions- und Reflexionskoeffizienten sind also gleich wie bei einer Barriere, sofern E > V 0 ist. Eine kurze Kontrolle zeigt, dass R + T = 1 ist, wir also keine Teilchen verlieren. Sowohl die Reflexion wie auch die Transmission oszillieren mit der Breite der Barriere a. Die Gleichungen können noch vereinfacht werden:
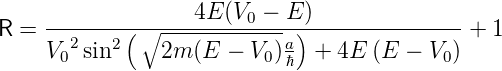 | (5.37) |
und
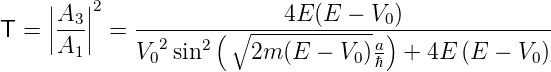 | (5.38) |
__________________________________________________________________________
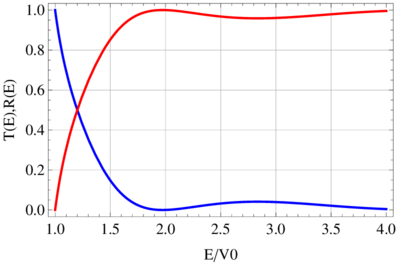
Transmission über einen Potentialtopf.
_____________________________________________________________________
Abbildung 5.10.3.1 zeigt den Transmissionskoeffizienten und den Reflexionskoeffizienten als Funktion der Energiedifferenz von E zu V 0.
Wenn die Energie des Teilchens E kleiner ist als die potentielle Energie der Wände E < V 0, kann die Schrödingergleichung mit dem allgemeinen Ansatz
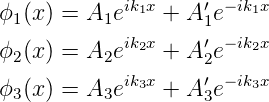 | (5.39) |
gelöst werden. Hier ist k1 = k3. Für x = 0 und x = a sind die Randbedingungen
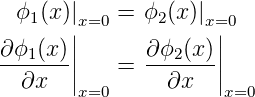 | (5.40) |
sowie
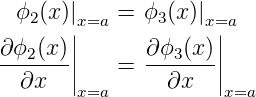 | (5.41) |
Von links und rechts kommen keine Wellen, also ist A1 = A′3 = 0. A2 oder A′2 können frei gewählt werden. Wir lassen A2 als freien Parameter. Dann ist bei x = 0
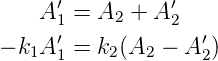 | (5.42) |
und bei x = a
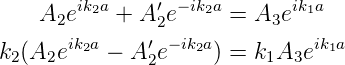 | (5.43) |
Beide Gleichungssysteme können gelöst werden und ergeben eine Beziehung zwischen A′1, A′2 als Funktion von A2 beziehungsweise für A3 und A′2 als Funktion von A2.
Die beiden Lösungen für A′2 müssen identisch sein, das heisst die Gleichung
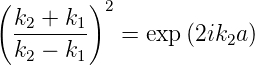 | (5.45) |
muss gelten. Da k2(E) und k1(E,V 0) beides Funktionen von
E sind, ist Gleichung (5.45) eine Bestimmungsgleichung für
die erlaubten Werte von E. Mit k2 = 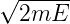 ∕ℏ und
k1 = i
∕ℏ und
k1 = i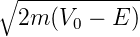 ∕ℏ (da E < V 0 ist) wird Gleichung
(5.45)
∕ℏ (da E < V 0 ist) wird Gleichung
(5.45)
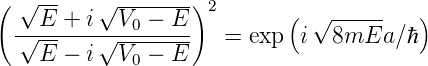 | (5.46) |
Gleichung (5.46) ist nicht analytisch lösbar. Bei den Lösungen muss sowohl der Realteil gleich sein wie auch der Imaginaärteil. Diese sind
Addiert man die quadrierte Gleichung (5.47a) zur quadrierten
Gleichung (5.47b), so erhält man 1 = 1. Es reicht also, die
numerische Lösung von Gleichung (5.47a) zu bestimmen. Mit
E∕V 0 = x2 und κ(V
0,a) = 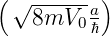 wird Gleichung
(5.47a)
wird Gleichung
(5.47a)
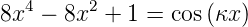 | (5.48) |
Die linke Seite der Gleichung ist invariant. x hat den
Wertebereich [0, 1). Die rechte Seite hängt von a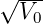 ab.
ab.
__________________________________________________________________________
Darstellung von 8x4 − 8x2 + 1 gegen cos(κx) in Abhängigkeit von κ
_______________________________________________________________
Abbildung 5.10.3.2 zeigt die linke und die rechte Seite der Gleichung 5.48. Die Schnittpunkte mit der roten Linie sind die Lösungen xi. Wenn κ zunimmt, gibt es mehr gebundene Lösungen. Ein zunehmendes κ bedeutet, dass entweder die Potentialtiefe V 0 zugenommen hat, oder aber die Breite des Topfes a.
__________________________________________________________________________
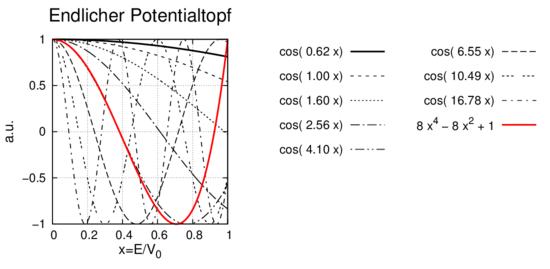
Nullstellen von 8x4 − 8x2 + 1 − cos(κx) = 0 in Abhängigkeit von κ
_______________________________________________________________
Abbildung 5.10.3.2 zeigt einen vergrösserten Ausschnitt zur Bestimmung der Nullstellen der Gleichung (5.48).
__________________________________________________________________________
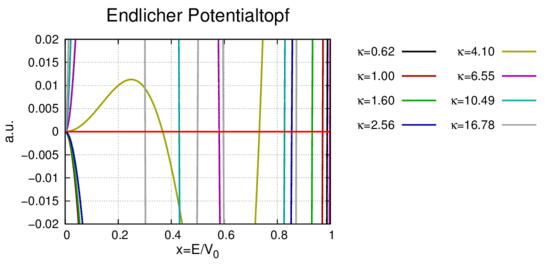
Relative Energieniveaus des Potentialtopfs als Funktion der Topfbreite a.
_____________________________________________________________________
Abbildung 5.10.3.2 zeigt die Energieniveaus bei konstantem V 0 als Funktion der Topfbreite a. Bei kleinem a existieren nur zwei Niveaus, E0 = 0 und E1 ≈V 0. Wenn a zunimmt, gibt es mehr Niveaus. Bei a = 4 a.u. sieht man, dass sich zwei Energieniveaus kreuzen. Bei einer vollen Betrachtung würde an dieser Stelle sich eine Bandlücke öffnen.
__________________________________________________________________________
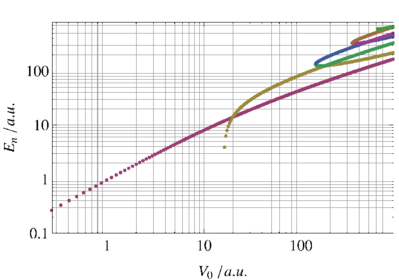
Energieniveaus des Potentialtopfs als Funktion der Wandhöhe V 0.
_____________________________________________________________________
Abbildung 5.10.3.2 zeigt die Energieniveaus bei konstantem a als Funktion der Wandhöhe V 0. Bei kleinem V 0 existieren nur zwei Niveaus, E0 = 0 (hier nicht angezeigt) und E1 ≈ V 0. Wenn V 0 zunimmt, gibt es mehr Niveaus. Die erste Kreuzung von energieniveaus sieht man bei V 0 = 16 a.u.
__________________________________________________________________________
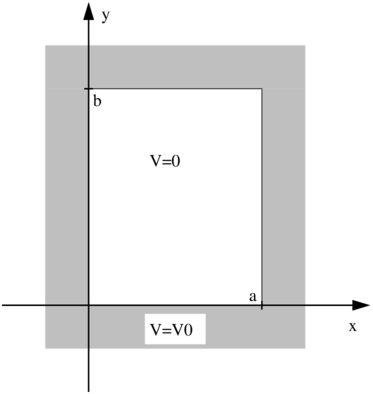
2D unendlicher Potentialkasten.
_____________________________________________________________________
Die Energieeigenwerte eines zweidimensionalen Potentialtopfs sind ähnlich quantisiert wie in dem Fall eines eindimensionalen Potentialtopfs mit unendlich hohen Wänden (siehe Abschnitt 5.7). Wenn der Topf die Dimensionen a und b hat (siehe Abbildung 5.10.4) sind die Energieeigenwerte
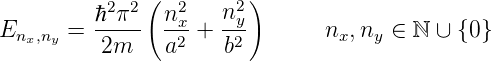 | (5.49) |
Die Eigenfunktionen lauten
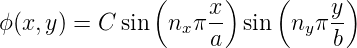 | (5.50) |
Wenn a∕b oder b∕a ganzzahlig sind, treten unterschiedliche Eigenfunktionen mit dem gleichen Energieeigenwert auf. Man sagt, die Eigenwerte seien entartet. Wenn zum Beispiel a∕b = 1 ist, dann sind die Energien zu den Eigenwerten (nx,ny) = (7, 1) und (nx,ny) = (5, 5) gleich.
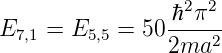 | (5.51) |
Beim eindimensionalen Potentialtopf mit endlichen Wandhöhen treten für gewisse Kombinationen von Topfbreiten a und Topfhöhen V 0 Kreuzungen von Niveaus auf. Dies führt wie gezeigt auch zu einer Entartung. Beim zweidimensionalen Potentialtopf mit endlich hohen Wänden tritt der gleiche Effekt auch auf.
 Lizenzinformationen
Lizenzinformationen