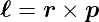

Als Literatur sind für dieses Kapitel insbesondere die Werke von Haken und Wolf[HW04], von Arfken und Weber[AW95] und das Internetskript von Komma[Kom96] zu empfehlen. In diesem Abschnitt wird die quantenmechanische Formulierung des Drehimpulses und seiner Anwendungen abgeleitet.
Klassisch ist der Bahndrehimpuls durch
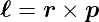 | (6.1) |
gegeben. In Komponenten geschrieben ist er
Wir ersetzen nun die Impulskomponenten durch die Operatoren
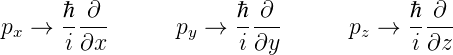
und erhalten für die Drehimpulsoperatoren
Das Quadrat des Drehimpulses ist
Für Vertauschungsrelationen zwischen den Operatoren Ω(1) und Ω(2) schreiben wir
![[ (1) (2)] (1) (2) (2) (1)
Ω ,Ω = Ω Ω − Ω Ω](ap-2015598x.png) | (6.7) |
Eine Möglichkeit diese Operatoren in Maple V zu definieren zeigt qm-defs.mw.
Nach den Rechnungen im Anhang F erhalten wir die Vertauschungsrelationen
Das elektrostatische Potential des Wasserstoffatoms für ein Elektron ist kugelsymmetrisch. Wir verwenden deshalb Kugelkoordinaten.
__________________________________________________________________________
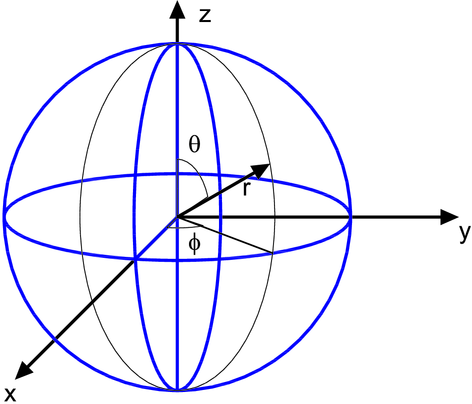
Definition der Kugelkoordinaten.
_____________________________________________________________________
Der Laplace-Operator in Kugelkoordinaten[BSMM08] ist
In Kugelkoordinaten lauten die Drehimpulsoperatoren
Die Schrödingergleichung für das Wasserstoffatom ist
![[ ]
ℏ2
− ----Δ + V(r) Ψ = EΨ
2me](ap-2015602x.png) | (6.11) |
wobei V (r) ein allgemeines, kugelsymmetrisches Potential ist.
Mit der Schreibweise von 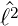 in Kugelkoordinaten (Gleichung
(6.10d)) und Gleichung (6.9)ist auch
in Kugelkoordinaten (Gleichung
(6.10d)) und Gleichung (6.9)ist auch
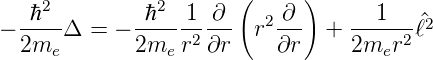 | (6.12) |
Wir beachten, dass Ableitungen nach einer Variablen ξ mit Funktionen vertauschen, die nicht von ξ abhängig sind und setzen
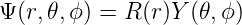 | (6.13) |
Die Schrödingergleichung des Wasserstoffatoms lautet dann
Da ![[ ]
ℓ^2, ^ℓz](ap-2015607x.png) = 0 ist, können sowohl die Eigenwerte von
= 0 ist, können sowohl die Eigenwerte von 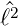 wie auch von
wie auch von 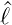 z gleichzeitig scharf gemessen werden. Mit
anderen Worten, die resultierende Wellenfunktion kann als
Produkt zweier Funktionen geschrieben werden.
z gleichzeitig scharf gemessen werden. Mit
anderen Worten, die resultierende Wellenfunktion kann als
Produkt zweier Funktionen geschrieben werden.
Eine scharf messbare Funktion bedeutet, dass es eine Eigenwertgleichung gibt. Wir haben also zwei dieser Eigenwertgleichungen:
wobei die Wahl des Eigenwertes ℏ2w, beziehungsweise ℏm aus Bequemlichkeit so gewählt wurde.
Nach Haken-Wolf [HW04, pp. 145-147] kann dies gezeigt
werden, indem wir auf Gleichung (6.15a) von links den
Operator 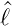 z und auf Gleichung (6.15b) von links den
Operator
z und auf Gleichung (6.15b) von links den
Operator 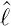 2 anwenden. Voraussetzung ist, dass Y (𝜃,ϕ)
sowohl eine Eigenfunktion von
2 anwenden. Voraussetzung ist, dass Y (𝜃,ϕ)
sowohl eine Eigenfunktion von 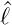 2 wie auch von
2 wie auch von 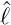 z ist, die
Erwartungswerte beider Grössen scharf gemessen werden
können.
z ist, die
Erwartungswerte beider Grössen scharf gemessen werden
können.
Wir subtrahieren Gleichung (6.16a) von Gleichung (6.16b) und erhalten
![^ℓ2^ℓY (𝜃,ϕ )− ^ℓ ^ℓ2Y (𝜃,ϕ) = (^ℓ2^ℓ − ^ℓℓ^2) Y (𝜃, ϕ) = [^ℓ2,ℓ^]
z z z z z
= ℏm ℏ2wY (𝜃,ϕ) − ℏ2w ℏmY (𝜃,ϕ )
( 2 2 )
= ℏm ℏ w − ℏ wℏm Y (𝜃,ϕ) = 0](ap-2015616x.png) | (6.17) |
Wenn also eine Wellenfunktion Y (𝜃,ϕ) eine Eigenfunktion zweier Operatoren ist, müssen die Operatoren kommutieren. Um zu zeigen, dass der verschwindende Kommutator zweier Operatoren bedeutet, dass alle Eigenfunktionen gemeinsam sind, kann wie im Buch von Schwindt [Sch13, pp. 53-57] vorgegangen werden.
m und w sind einheitenlose Zahlen, die noch bestimmt werden
müssen. Eine Mapledatei zum Berechnen der Lösungen
(Orbitale) ist hydrogen.mw. Das Original stammt von Prof.
i.R. Dr. rer.nat.Fritz Metz von der Universität Konstanz
https://www.chemie.uni-konstanz.de/forschung/arbeitsgruppen/ehemalige-
arbeitsgruppenleiter/. und hiess „hydrogen.mws“. Die
Webseite ist seit 2016 leider nicht mehr zugänglich.
Unter der Annahme, dass w bekannt ist, lautet die Gleichung für den Radialteil
![[ ( ) ]
ℏ2 1 ∂ ∂ ℏ2w
− ---- -2--- r2--- + V (r) + -----2 R (r) = E ·R (r)
2me r ∂r ∂r 2mer](ap-2015617x.png) | (6.18) |
wobei me zum Beispiel die Masse eines Elektrons ist. Prinzipiell könnte me aber auch die Masse jedes anderen passenden Elementarteilchens sein. Nach Arfken und Weber[AW95, 736] schreibt man
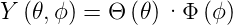 | (6.19) |
Die Kugelflächenfunktion Y 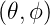 wird als Produkt einer
nur vom Winkel zum „Nordpol“ abhängigen Funktion Θ
wird als Produkt einer
nur vom Winkel zum „Nordpol“ abhängigen Funktion Θ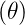 und einer azimutalen Funktion Φ
und einer azimutalen Funktion Φ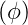 . Aus Gleichung (6.15b)
folgt
. Aus Gleichung (6.15b)
folgt
und
Weiter bekommt man für den azimutalen Anteil der Wellenfunktion
Die Lösungen der Gleichung (6.22) sind
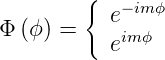 | (6.23) |
Dies sind orthogonale Funktionen, da
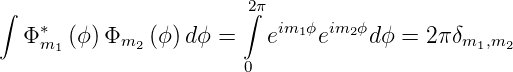 | (6.24) |
Wenn der Raum um den Winkel ϕ = 2π gedreht wird, muss aus Symmetriegründen wieder eine zur ursprünglichen Funktion identische Observable Φ∗Φ entstehen. Also muss
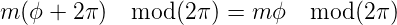 | (6.25) |
sein. Die Funktion Modulo trägt der Tatsache Rechnung,
dass die Winkelfunktionen 2π-periodisch sind. Gleichung
(6.25) gilt dann, wenn m ganzzahlig ist. Die Observable ist
dann auf dem Intervall 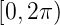 eindeutig bestimmt.
eindeutig bestimmt.
Wenn die Transformationseigenschaft des Wellenfunktion so wäre, dass der Erwartungswert, also die Observable, bei einer Drehung um 2π das Vorzeichen wechselt, dann könnte m auch halbzahlig sein: Dies wäre dann eine Spinfunktion.
Wir kennen nun m. Um w und Θ(𝜃) zu bestimmen, subtrahieren wir Gleichung (6.21) von (6.15a)
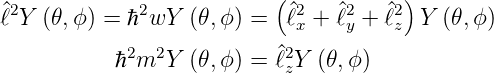
Für Y (𝜃,ϕ) = Θ(𝜃)Φ(ϕ) ergibt sich
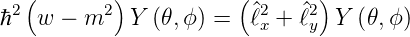 | (6.26) |
Es hat sich eingebürgert, die folgenden Bezeichnungen zu verwenden
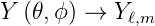 | (6.27) |
Um eine Beziehung zwischen w und m zu erhalten, multiplizieren wir von links mit Y ∗(𝜃,ϕ) und integrieren über die Kugeloberfläche. Weiter schreiben wir anstelle von w wℓ um klarzumachen, dass eine Abhängigkeit von ℓ besteht und dass wℓ keine Kreisfrequenz ist.
Hier wurde die Seite mit wℓ −m2 berechnet. Die noch nicht berechnete rechte Seite besteht aus zwei addierten Integralen. Wir brauchen die Operatoren
und damit
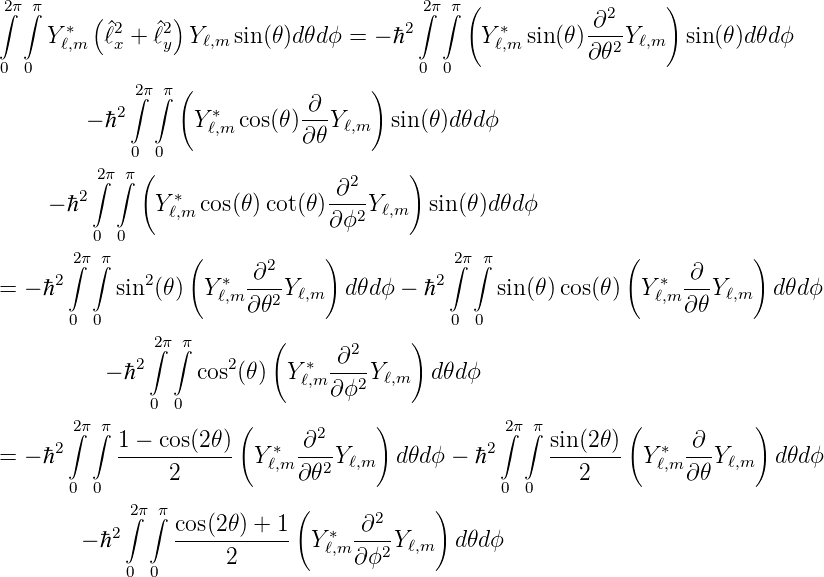 | (6.32) |
Durch partielle Integration folgt nach Haken, Wolf[HW04], dass das Integral in (6.32) über 𝜃 und ϕ ≥ 0 ist. Damit ist mit (6.28)
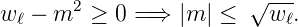 | (6.33) |
Mit der Identität
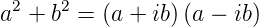 | (6.34) |
kann man die Operatoren
definieren. Es folgt
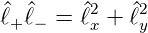 | (6.36) |
und weiter
Wir wenden 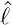 ± auf
± auf 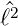 Y ℓ,m an
Y ℓ,m an
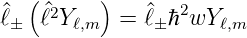 | (6.38) |
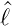 ± und
± und 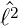 sind vertauschbar, also gilt
sind vertauschbar, also gilt
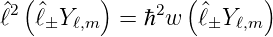 | (6.39) |
d.h. wenn Y ℓ,m eine Eigenfunktion von 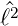 ist, dann ist auch
ist, dann ist auch
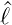 ±Y ℓ,m eine Eigenfunktion von
±Y ℓ,m eine Eigenfunktion von 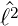 . Aus der Azimutalgleichung
(6.15b) erhalten wir
. Aus der Azimutalgleichung
(6.15b) erhalten wir
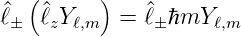 | (6.40) |
sowie aus Gleichung (6.37b)
Also ist
 | (6.42) |
und
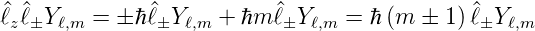 | (6.43) |
Damit ist auch 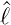 ±Y ℓ,m eine noch nicht normierte
Eigenfunktion zur Azimutalgleichung, aber mit dem neuen
Eigenwert ℏ(m ± 1). Die Normierung kann über
±Y ℓ,m eine noch nicht normierte
Eigenfunktion zur Azimutalgleichung, aber mit dem neuen
Eigenwert ℏ(m ± 1). Die Normierung kann über
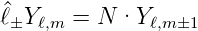 | (6.44) |
berechnet werden, wobei N eine Normierungskonstante ist.
Weiter gilt die folgende Beziehung:
In einem Magnetfeld ist die Frequenzänderung der Übergänge in einem Atom proportional zu m (Zeemanneffekt, siehe Abschnitt 6.5.3). Da für ein endliches Magnetfeld diese Änderungen endlich sein müssen, fordern wir, dass es für m Minimal- und Maximalwerte geben muss. Dann gilt auch
Da Y ℓ,mmax ⇔ 0 ist, folgt
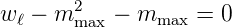 | (6.47) |
Aus
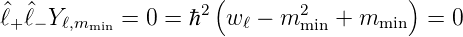 | (6.48) |
folgt weiter
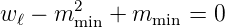 | (6.49) |
Löst man Gleichung (6.47) und Gleichung (6.49) beide wℓ auf und setzt sie gleich, erhält man
Da mmax ≥ mmin ist, folgt mmax + mmin = 0. Wegen
Gleichung (6.44) erhöht sich m bei jeder Anwendung von 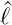 +
auf Y ℓ,m um den Wert eins. Deshalb muss mmax −mmin eine
ganze Zahl sein. Dies geht nur, wenn
+
auf Y ℓ,m um den Wert eins. Deshalb muss mmax −mmin eine
ganze Zahl sein. Dies geht nur, wenn
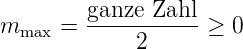 | (6.51) |
mindestens halbzahlig ist.
Andererseits muss Φ∗Φ auf dem Intervall 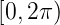 eindeutig
und stetig differenzierbar sein (unabhängig von der Wahl
des Nullpunktes). Deshalb muss m ganzzahlig sein. Wir
definieren: mmax = ℓ ∈ℕ∪{0}.
eindeutig
und stetig differenzierbar sein (unabhängig von der Wahl
des Nullpunktes). Deshalb muss m ganzzahlig sein. Wir
definieren: mmax = ℓ ∈ℕ∪{0}.
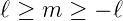 | (6.52) |
mit
Damit haben wir die beiden Eigenwertgleichungen
und
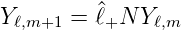 | (6.55) |
mit der Normierung
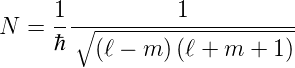 | (6.56) |
Die Tatsache, dass auch halbzahlige ℓ eine Lösung sein könnten, wenn nur die Eindeutigkeitsbedingung für m erfüllt wäre, deutet darauf hin, dass es eventuell noch weitere Effekte geben könnte. Zum Beispiel ermöglicht das Elektron mit seinem halbzahligen Eigendrehimpuls diese zusätzlichen Lösungen.
Die bis jetzt in kartesischen Koordinaten definierten Drehimpulsoperatoren können auch durch die Differentialoperatoren in Kugelkoordinaten ausgedrückt werden.
Wir wissen schon, dass Y ℓ,m die Form
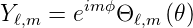 | (6.58) |
haben muss. Wir setzen nach Arfken und Weber [AW95]
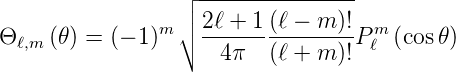 | (6.59) |
Pℓm(x) ist eine zugeordnete Legendre-Funktion, die aus der Legendre-Funktion mit
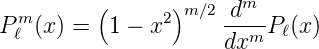 | (6.60) |
berechnet werden kann. Die Definition der Legendre-Funktion lautet [AW95]
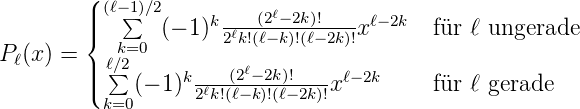 | (6.61) |
Weiter muss
sein. Wir berechnen nun, welche Wirkung die Erzeugungs- und Vernichtungsoperatoren ausüben. In sphärischen Koordinaten haben wir
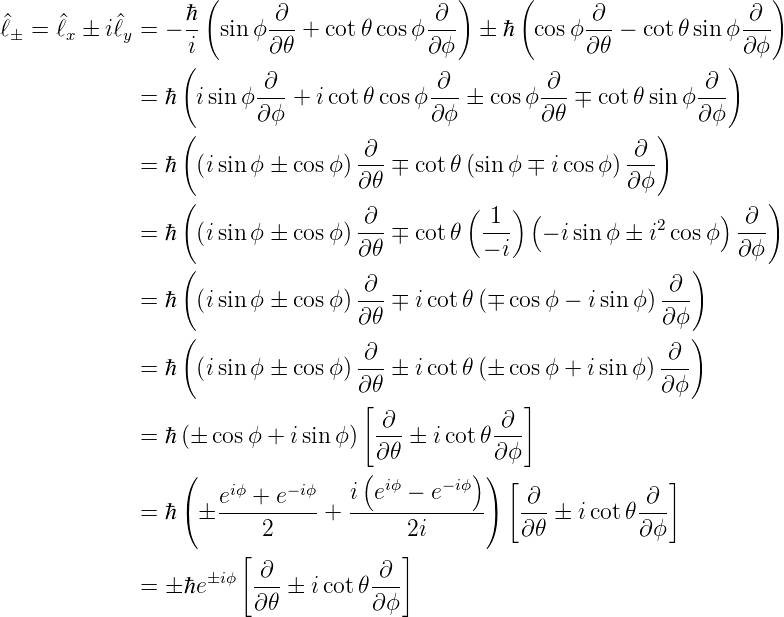
Wir setzen in die beiden Relationen für 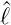 − und
− und 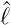 + die
Funktion Y ℓ,m = eimϕΘ
ℓ,m(𝜃) ein und erhalten
+ die
Funktion Y ℓ,m = eimϕΘ
ℓ,m(𝜃) ein und erhalten
Für m = −ℓ wird
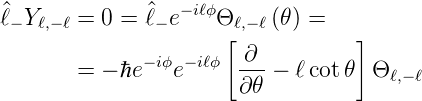
Wir erhalten die Differentialgleichung
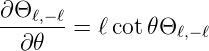 | (6.64) |
Deren Lösung lautet
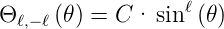 | (6.65) |
Die Lösungen müssen normiert sein, also ist
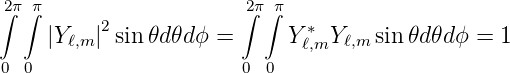 | (6.66) |
Deshalb ist die Integrationskonstante aus Gleichung (6.65)
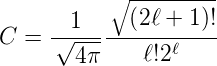 | (6.67) |
Mit dem Erzeugungsoperator
![[ ]
^ iϕ -∂-
ℓ+Yℓ,m = ℏe ∂ 𝜃 − m cot 𝜃 Y ℓ,m](ap-2015684x.png) | (6.68) |
können alle Funktionen konstruieren werden. Wenn ℓ = 0 ist, ist
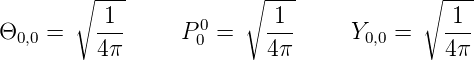
Mit den Rekursionsrelationen erhalten wir
Darstellungen dieser Wellenfunktionen finden Sie im Anhang A.1.
Der Radialteil der Wellenfunktion (6.14) ist
![[ 2 ( ) 2 ]
− -ℏ---1 d-- r2-d- + ℏ-ℓ-(ℓ +-1) + V (r) R (r) = E·R (r)
2me r2 dr dr 2mer2](ap-2015687x.png) | (6.70) |
Diese Gleichung gilt für alle sphärisch symmetrischen Potentiale. Wir verwenden
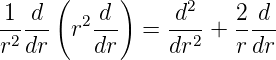 | (6.71) |
und Multiplizieren die Gleichung (6.70) mit 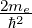
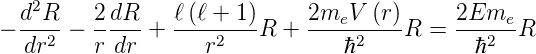 | (6.72) |
wir setzen
und erhalten aus Gleichung (6.72) die skalierte Gleichung
![2 [ ]
d-R- + 2-dR- + A − V^ (r) − ℓ-(ℓ +-1) R = 0
dr2 r dr r2](ap-2015692x.png) | (6.75) |
Wir betrachten den Grenzfall: r−→∞ und verwenden den
Ansatz R =  . Für die Ableitungen gilt
. Für die Ableitungen gilt
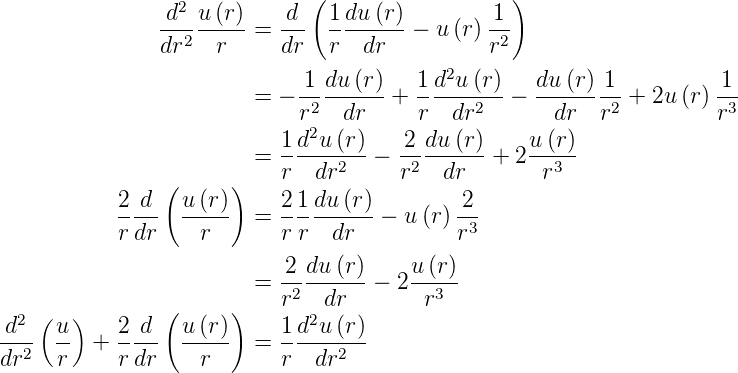
Zusammen erhalten wir
oder mit r ⇔ 0
![[ ]
d2u ℓ(ℓ + 1 )
--2-+ A − ^V (r) − ----2--- u = 0
dr r](ap-2015696x.png) | (6.77) |
Im Grenzfall r → ∞ muss das Potential null sein, also
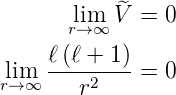
Im Grenzfall r →∞ lautet Gleichung (6.77)
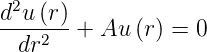 | (6.78) |
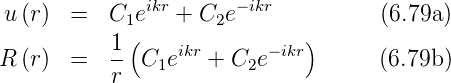
Zusammen mit der zeitlichen Lösung 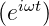 haben wir
ein- und auslaufende Kugelwellen.
haben wir
ein- und auslaufende Kugelwellen.
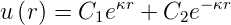 | (6.80) |
Da die Lösung für r →∞ gegen Null gehen muss, muss C1 = 0 sein. Also ist
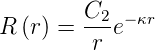 | (6.81) |
die Lösung für gebundene Zustände.
Die gefundenen allgemeinen Lösungen gelten nur für r →∞. Die Form der Lösung hängt allein von der Asymptotik des Potentials ab. Die Lösungen für r → 0 hängen jedoch von der Form des Potentials V (r) ab und sind für jedes Potential anders.
Mit den allgemeinen Lösungen für ein beliebiges Potential V (r) können wir nun die Lösungen für das Wasserstoffatom berechnen
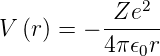 | (6.82) |
Wir wenden die Variablentransformation
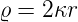 | (6.83) |
mit der Definition für E < 0 aus Gleichung (6.73)
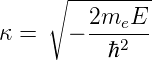 | (6.84) |
Weiter setzen wir
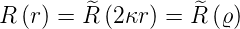 | (6.85) |
Mit
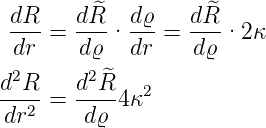
wird der Radialteil der Wellengleichung (6.70)
mit
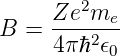 | (6.87) |
Zur Lösung von Gleichung (6.86) verwenden wir den Exponentialansatz
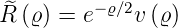 | (6.88) |
Zuerst berechnen wir die einzelnen Ableitungen
Wir setzen den Exponentialansatz in Gleichung (6.86) ein, verwenden die Ableitungen aus Gleichung (6.89) und spalten e−ϱ∕2 > 0 ab.
Gleichung (6.90) kann mit dem Rekursionsansatz gelöst werden
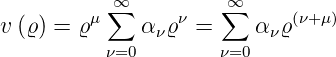 | (6.91) |
wobei α0 ⇔ 0 ist. Eingesetzt erhalten wir
Für ν = 0 tritt nur μ auf. Für ν = 0 bekommen wir
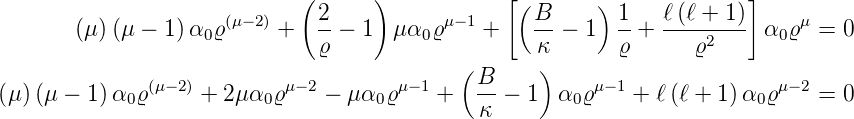
Die Gleichung gilt dann allgemein, wenn die Koeffizienten von ϱμ−2 für jedes ν getrennt gleich null sind. Wir erhalten so eine Gleichung für μ
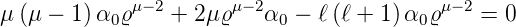 | (6.93) |
Vereinfacht erhalten wir
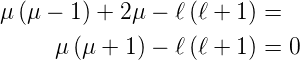
Wir wissen aus den Lösungen für Y ℓ,m, dass ℓ ≥ 0 ist. Die Lösungen für μ sind
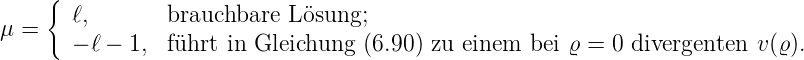 | (6.94) |
Die Bestimmungsgleichungen enthalten für μ bei ν = 0 enthalten auch höhere Potenzen von ϱ. Diese sind aber nicht vollständig, da auch die Summanden bei ν = 1 Koeffizienten mit diesen Potenzen haben. Nun kann man in Gleichung (6.92) μ = ℓ einsetzen und für ein bestimmtes ν die Beziehungen zwischen den ανs aufschreiben. Die Vorfaktoren des niedrigsten Exponenten ν + ℓ − 2 liefern eine Rekursionsgleichung
Wir setzen
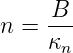 | (6.96) |
wobei κ durch κn ersetzt wurde, da κ von n abhängt. Mit dieser Abkürzung erhält man aus Gleichung (6.95)
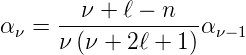 | (6.97) |
Es gibt 2 Lösungstypen:
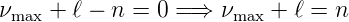 | (6.98) |
Aus dem Zähler von Gleichung (6.97) ergibt sich die Forderung
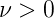 | (6.99) |
Also ist das ganzzahlige ν mindestens eins. Zusammen erhalten wir aus (6.98) und (6.99) die Bedingung
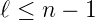 | (6.100) |
In der ganzen Rekursionskette ist α0 frei wählbar. Dieser Koeffizient ergibt die Amplitude. Die ersten αν sind für α0 = 1
___________________________________________________________________________
| n = 1 | n = 2 | n = 3 | ||||||||
| ℓ = | 0 | 0 | 1 | 0 | 1 | 2 | 0 | 1 | 2 | 3 |
| ν = 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| ν = 1 | 0 | −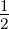 | 0 | −1 | −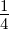 | 0 | −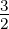 | −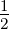 | −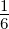 | 0 |
| ν = 2 | 0 | 0 | 0 | 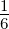 | 0 | 0 | 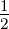 | 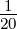 | 0 | 0 |
| ν = 3 | 0 | 0 | 0 | 0 | 0 | 0 | −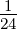 | 0 | 0 | 0 |
| ν = 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
_____________________________________________________________________
| Die ganzzahligen Indizes heissen
|
Die zu den Haupt- und Drehimpulsquantenzahlen gehörigen nicht normierten Funktionen sind
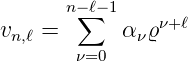 | (6.101) |
___________________________________________________________________________
| n | ℓ | vn,ℓ |
| 1 | 0 | v1,0 = α0ϱ0+0 = 1 |
| 2 | 0 | v2,0 = α0ϱ0+0 + α
1ϱ1+0 = 1 −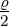 |
| 1 | v2,1 = α0ϱ0+1 = ϱ | |
| 3 | 0 | v3,0 = α0ϱ0+0 + α
1ϱ1+0 + α
2ϱ2+0 = 1 −ϱ + 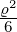 |
| 1 | v3,1 = α0ϱ0+1 + α
1ϱ1+1 = ϱ −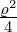 |
|
| 2 | v3,2 = α0ϱ0+2 = ϱ2 | |
| 4 | 0 | v4,0 = α0ϱ0+0 + α
1ϱ1+0 + α
2ϱ2+0 + α
3ϱ3+0 = 1 −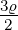 + + 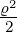 − −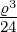 |
| 1 | v4,1 = α0ϱ0+1 + α
1ϱ1+1 + α
2ϱ2+1 = ϱ −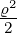 + + 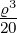 |
|
| 2 | v4,2 = α0ϱ0+2 + α
1ϱ1+2 = ϱ2 −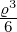 |
|
| 3 | v4,3 = α0ϱ0+3 = ϱ3 | |
_______________________________________________________________
Die normierten radialen Eigenfunktionen als Funktion der dimensionslosen Variablen ϱ sind
___________________________________________________________________________
| n | ℓ | 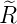 n,l(ϱ) n,l(ϱ) |
| 1 | 0 | 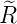 1,0(ϱ) = 1,0(ϱ) = 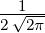 e−ϱ∕2 e−ϱ∕2 |
| 2 | 0 | 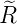 2,0(ϱ) = 2,0(ϱ) = 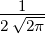 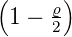 e−ϱ∕2 e−ϱ∕2 |
| 1 | 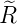 2,1(ϱ) = 2,1(ϱ) = 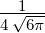 ϱe−ϱ∕2 ϱe−ϱ∕2 |
|
| 3 | 0 | 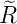 3,0(ϱ) = 3,0(ϱ) = 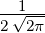 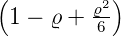 e−ϱ∕2 e−ϱ∕2 |
| 1 | 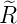 3,1(ϱ) = 3,1(ϱ) = 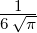 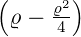 e−ϱ∕2 e−ϱ∕2 |
|
| 2 | 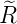 3,2(ϱ) = 3,2(ϱ) = 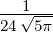 ϱ2e−ϱ∕2 ϱ2e−ϱ∕2 |
|
| 4 | 0 | 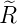 4,0(ϱ) = 4,0(ϱ) = 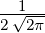 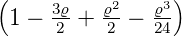 e−ϱ∕2 e−ϱ∕2 |
| 1 | 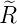 4,1(ϱ) = 4,1(ϱ) = 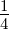 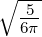 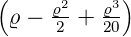 e−ϱ∕2 e−ϱ∕2 |
|
| 2 | 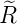 4,2(ϱ) = 4,2(ϱ) = 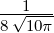 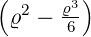 e−ϱ∕2 e−ϱ∕2 |
|
| 3 | 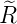 4,3(ϱ) = 4,3(ϱ) = 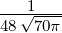 ϱ3e−ϱ∕2 ϱ3e−ϱ∕2 |
|
| 5 | 0 | 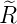 5,0(ϱ) = 5,0(ϱ) = 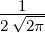 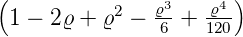 e−ϱ∕2 e−ϱ∕2 |
| 1 | 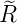 5,1(ϱ) = 5,1(ϱ) = 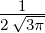 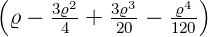 e−ϱ∕2 e−ϱ∕2 |
|
| 2 | 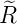 5,2(ϱ) = 5,2(ϱ) = 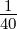 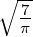 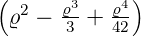 e−ϱ∕2 e−ϱ∕2 |
|
| 3 | 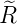 5,3(ϱ) = 5,3(ϱ) = 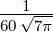 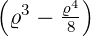 e−ϱ∕2 e−ϱ∕2 |
|
| 4 | 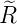 5,4(ϱ) = 5,4(ϱ) = 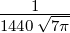 ϱ4e−ϱ∕2 ϱ4e−ϱ∕2 |
_______________________________________________________________
_______________________________________________________________
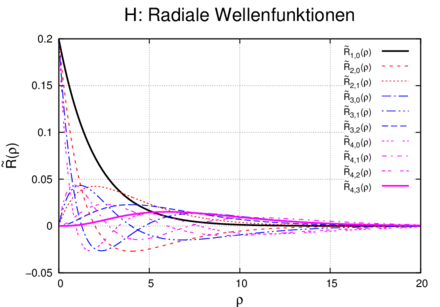
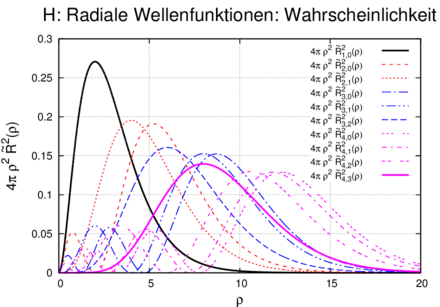
Oben: normierte radiale Wellenfunktionen  des
Wasserstoffs. Unten: Wahrscheinlichkeitsdichte
4πϱ2
des
Wasserstoffs. Unten: Wahrscheinlichkeitsdichte
4πϱ2 1,02(ϱ) der Wasserstoffwellenfunktionen abhängig
vom Kernabstand.
1,02(ϱ) der Wasserstoffwellenfunktionen abhängig
vom Kernabstand.
_____________________________________________________________________
Abbildung 6.3.2.3 zeigt für n = 1 bis n = 4 die radialen
normierten Wellenfunktionen des Wasserstoffs. 4πϱ2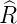 1,02(ϱ)
hat bei ϱ = 2 ein Maximum. Das bedeutet, dass das
Wasserstoffatom im Grundzustand etwa einen Durchmesser
von 106 pm hat (siehe auch Gleichung (6.108)), was eben
ϱ = 2 entspricht. Der Kerndurchmesser ist 105 mal kleiner,
also in der Darstellung nicht sichtbar.
1,02(ϱ)
hat bei ϱ = 2 ein Maximum. Das bedeutet, dass das
Wasserstoffatom im Grundzustand etwa einen Durchmesser
von 106 pm hat (siehe auch Gleichung (6.108)), was eben
ϱ = 2 entspricht. Der Kerndurchmesser ist 105 mal kleiner,
also in der Darstellung nicht sichtbar.
Mit der Rücksubstitution ϱ = 2κnr bekommen wir die radialen Eigenfunktionen des Wasserstoffatoms
___________________________________________________________________________
| n | ℓ | Rn,l(r) |
| 1 | 0 | R1,0(r) = 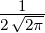 e−κ1r e−κ1r |
| 2 | 0 | R2,0(r) = 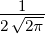 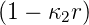 e−κ2r e−κ2r |
| 1 | R2,1(r) = 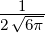 κ2re−κ2r κ2re−κ2r |
|
| 3 | 0 | R3,0(r) = 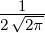 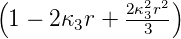 e−κ3r e−κ3r |
| 1 | R3,1(r) = 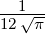 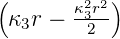 e−κ3r e−κ3r |
|
| 2 | R3,2(r) = 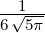 κ32r2e−κ3r κ32r2e−κ3r |
|
| 4 | 0 | R4,0(r) = 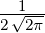 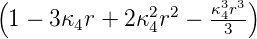 e−κ4r e−κ4r |
| 1 | R4,1(r) = 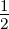 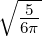 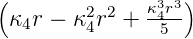 e−κ4r e−κ4r |
|
| 2 | R4,2(r) = 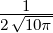 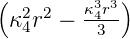 e−κ4r e−κ4r |
|
| 3 | R4,3(r) = 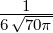 κ43r3e−κ4r κ43r3e−κ4r |
|
| 5 | 0 | R5,0(r) = 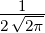 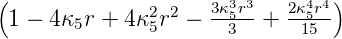 e−κ5r e−κ5r |
| 1 | R5,1(r) = 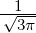 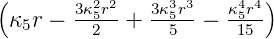 e−κ5r e−κ5r |
|
| 2 | R5,2(r) = 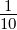 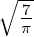 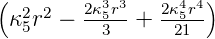 e−κ5r e−κ5r |
|
| 3 | R5,3(r) = 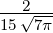 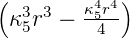 e−κ5r e−κ5r |
|
| 4 | R5,4(r) = 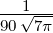 κ54r4e−κ5r κ54r4e−κ5r |
_____________________________________________________________________
Die Konstante κn in Tabelle 6.3.2.3 ist
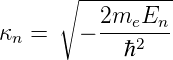 |
gesetzt. Mit Gleichung (6.87) und Gleichung (6.96) kann der n-te Energieeigenwert berechnet werden.
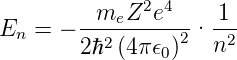 | (6.102) |
Wir können nun auch κn mit En ausdrücken
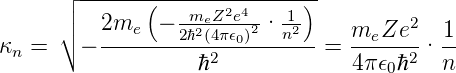 | (6.103) |
Schliesslich haben wir
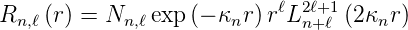 | (6.104) |
Dabei ist Nn,ℓ ein Normierungsfaktor und
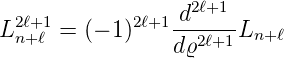 | (6.105) |
eine Funktion (zugeordnetes Laguerre-Polynom), die aus einem Laguerrschen Polynom
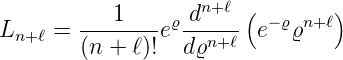 | (6.106) |
durch Ableiten erzeugt werden kann.
Die Grösse
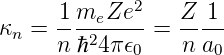 | (6.107) |
ist ein inverser Radius. Der Kehrwert 1∕κn gibt die radiale Längenskala der Wellenfunktion dar. Je grösser κn ist, desto näher zum Kern wird die Wellenfunktion zusammengedrückt. Bei Integraltransformationen wie der Fouriertransformation tauchen äquivalente Grössen auf: Dort werden sie Wellenzahlen genannt.
Der inverse Radius κn hängt von der 1∕n ab und der Kernladung Z ab. Der von der Quantenzahl n und der Kernladungszahl Z unabhängige Radius a0, der Bohrsche Radius, hat den Wert
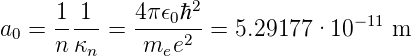 | (6.108) |
___________________________________________________________________________
| n | ℓ | Rn,ℓ(r) |
| 1 | 0 | R1,0(r) = 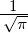 κ13∕2e−κ1r = κ13∕2e−κ1r = 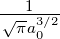 e−r∕a0 e−r∕a0 |
| 2 | 0 | R2,0(r) = 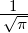 κ23∕2 κ23∕2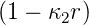 e−κ2r = e−κ2r = 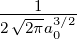 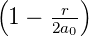 e−r∕(2a0) e−r∕(2a0) |
| 1 | R2,1(r) = 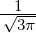 κ23∕2κ
2re−κ2r = κ23∕2κ
2re−κ2r = 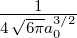 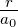 e−r∕(2a0) e−r∕(2a0) |
|
| 3 | 0 | R3,0(r) = 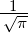 κ33∕2 κ33∕2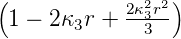 e−κ3r = e−κ3r = 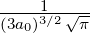 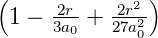 e−r∕(3a0) e−r∕(3a0) |
| 1 | R3,1(r) = 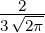 κ33∕2 κ33∕2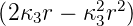 e−κ3r = e−κ3r = 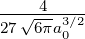 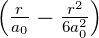 e−r∕(3a0) e−r∕(3a0) |
|
| 2 | R3,2(r) = 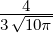 κ33∕2κ
32r2e−κ3r = κ33∕2κ
32r2e−κ3r = 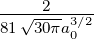 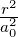 e−r∕(3a0) e−r∕(3a0) |
|
| 4 | 0 | R4,0(r) = 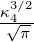 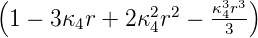 e−κ4r = e−κ4r = 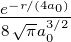 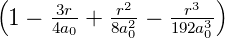 |
| 1 | R4,1(r) = 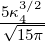 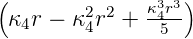 e−κ4r = e−κ4r = 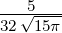 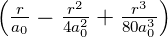 e−r∕(4a0) e−r∕(4a0) |
|
| 2 | R4,2(r) = 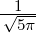 κ43∕2 κ43∕2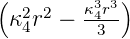 e−κ4r = e−κ4r = 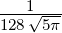 κ43∕2 κ43∕2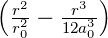 e−r∕(4a0) e−r∕(4a0) |
|
| 3 | R4,3(r) = 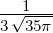 κ43∕2κ
43r3e−κ4r = κ43∕2κ
43r3e−κ4r = 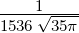 κ43∕2 κ43∕2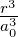 e−r∕(4a0) e−r∕(4a0) |
|
_____________________________________________________________________
Die normierten radialen Wellenfunktionen sind in Tabelle 6.3.2.3 dargestellt. Bei Hyperphysics gibt es eine schöne Darstellung dieser Funktionen. Eine Skizze dieser Wellenfunktionen findet sich auch im Anhang A.2.
Die vollständige Wellenfunktion eines durch n, ℓ und m gegebenen Zustandes eines Wasserstoffatoms ist
mit
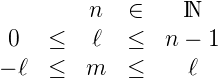 |
Die Wasserstoffwellenfunktion ist dann
|
wobei
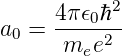
der Bohrsche Radius und
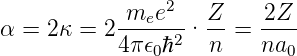
ist. Die Wasserstofforbitale[AW95] sind
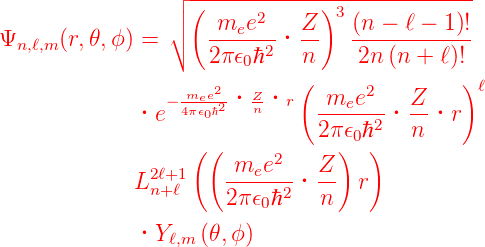
|
Es gibt Autoren, die schreiben
|
| Versuch zur Vorlesung: | |
| Orbitalmodelle: Stehende Wellen auf runder Wasseroberfläche (Versuchskarte AT-60) | |
| Versuch zur Vorlesung: | |
| Orbital-Modelle: Styropormodelle von Ladungswolken (Versuchskarte AT-61) | |
Die folgende Ausarbeitung folgt der Behandlung von Gordon Baym[Bay69, 66]. Eine analoge Darstellung findet sich im Buch von Landau und Lifschitz [LL79, 46].
In der Quantenmechanik ist es üblich Skalarproduckte mit Brakets zu beschreiben. Die Definitionen sind:
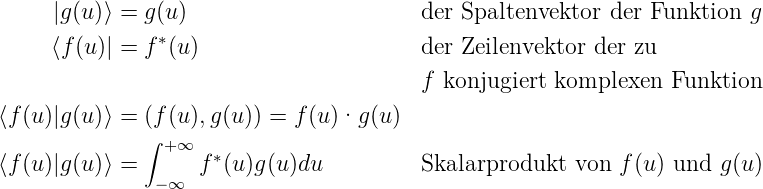
Ohne Angabe der Variablen (man muss sie sich denken!) kann auch geschrieben werden
Nun seien 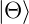 und
und 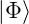 normierte Wellenfunktionen, das
heisst
normierte Wellenfunktionen, das
heisst 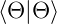 = 1 und
= 1 und 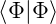 = 1.
= 1.
Behauptung:
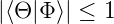 | (6.113) |
Beweis:
Sei
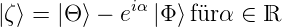 |
Die Reihenfolge der Wellenfunktionen darf nicht geändert werden, Zahlen dürfen vor das Skalarprodukt gezogen werden. Dann ist
Gleichheit gilt also nur, wenn 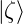 = 0. Wir erinnern uns an
die Definition des Skalarproduktes in (6.112). Deshalb
gilt
= 0. Wir erinnern uns an
die Definition des Skalarproduktes in (6.112). Deshalb
gilt
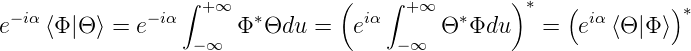 | (6.115) |
In (6.114) ist die rechte Seite eine reelle Zahl, aufgrund der Konstruktion der Gleichung. Nach dieser Überlegung, und nach Gleichung (6.115) haben die Imaginärteile der beiden Summanden unterschiedliches Vorzeichen, sind aber gleich gross. Wir wählen das beliebige α so, dass
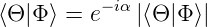 | (6.116) |
ist. Dann kann die letzte Zeile von Gleichung (6.114) so umgeschrieben werden:
Damit ist die Behauptung gezeigt:
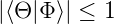 | (6.118) |
Bei nicht normierten Funktionen verwendet man
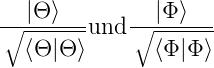 |
Aus Gleichung (6.113) erhält man
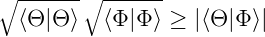 | (6.119) |
Aus Gleichung (6.114) erhält man
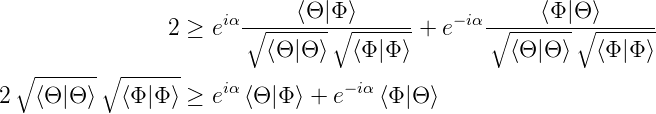
und damit
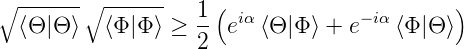 | (6.120) |
Die Standardabweichungen der Wellenfunktion  der
Orts- und Impulsoperatoren sind
der
Orts- und Impulsoperatoren sind
wobei für die Erwartungswerte wie üblich nach Gleichung (6.112) gilt:
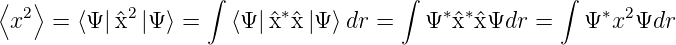 |
Wir nehmen an, dass das zu untersuchende Teilchen die
Wellenfunktion 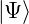 hat. Wir definieren
hat. Wir definieren
Dann ist mit der Definition des Skalarproduktes (6.112)
Aus Gleichung (6.120) erhält man mit eiα = −i und der
Annahme, dass 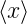 = 0 und
= 0 und 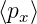 = 0 (was sich immer durch
eine Galilei-Transformation erreichen lässt.)
= 0 (was sich immer durch
eine Galilei-Transformation erreichen lässt.)
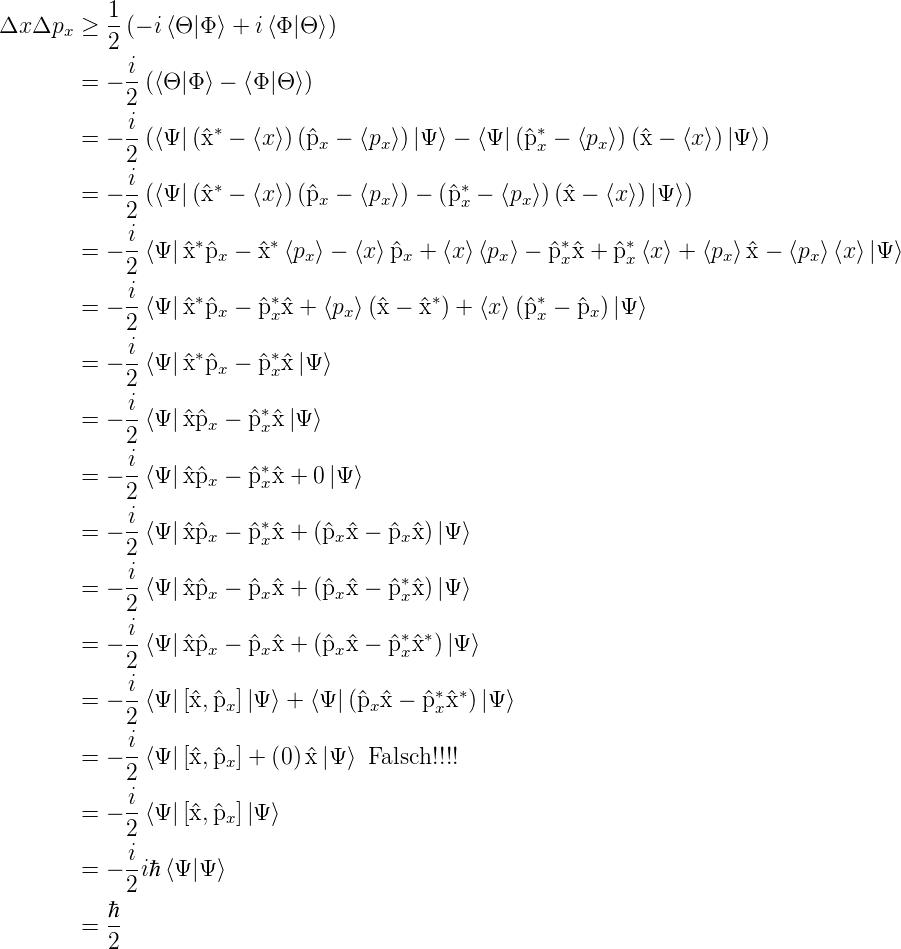
Unschärferelation oder Unbestimmtheitsrelation
|
Wir haben bei der Berechnung mit den Operatoren 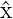 und
und
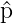 x verwendet, dass
x verwendet, dass 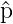 x rein imaginär ist.
x rein imaginär ist.
Nach Landau und Lifschitz [LL79, 46] folgt aus
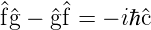 | (6.125) |
wobei 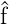 und
und 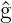 beliebige Operatoren zu den klassischen
Grössen f und g sind und bei der
beliebige Operatoren zu den klassischen
Grössen f und g sind und bei der 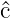 der Operator zur
klassischen Grösse c (der Poisson-Klammer) ist, dass im
klassischen Grenzfall alle Operatoren vertauschbar sind. In
zweiter Näherung kann der Operator
der Operator zur
klassischen Grösse c (der Poisson-Klammer) ist, dass im
klassischen Grenzfall alle Operatoren vertauschbar sind. In
zweiter Näherung kann der Operator 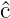 als Multiplikation mit
c aufgefasst werden, so dass
als Multiplikation mit
c aufgefasst werden, so dass
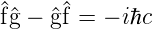 | (6.126) |
und in Analogie zu den Impulsen
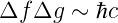 | (6.127) |
Man schliesst also, dass für allgemeine Operatoren 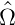 1 und
1 und
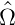 2, bei denen man über eine Transformation
2, bei denen man über eine Transformation 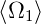 = 0 und
= 0 und
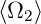 = 0 erreichen kann, die Unbestimmtheitsrelation
gilt
= 0 erreichen kann, die Unbestimmtheitsrelation
gilt
|
Für allgemeine durch Matrizen dargestellte Operatoren
muss die komplexe Konjugation 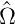 ∗
durch die Adjungation
∗
durch die Adjungation 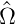 †
ersetzt werden, also durch die Transposition der Matrix und
der gleichzeitigen Konjugation.
†
ersetzt werden, also durch die Transposition der Matrix und
der gleichzeitigen Konjugation.
Beim Wasserstoffatom hatten wir drei Quantenzahlen
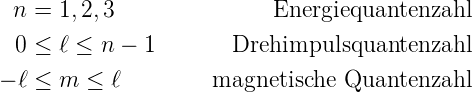
Diese drei Quantenzahlen beschreiben den atomaren Zustand des Wasserstoffatoms. Das Rydberg-Gesetz besagt, dass für hochangeregte Zustände nur die Energiequantenzahl n wichtig sei. Das bedeutet, dass alle Drehimpuls- oder ℓ- und alle magnetischen oder m-Zustände die gleiche Energie haben.
| Zustände zu verschiedenem ℓ oder m, die alle die gleiche Energie haben, heissen entartet. Die Anzahl Zustände bei verschiedenem ℓ oder m mit der gleichen Energie ist die Entartung. |
Es stellen sich die folgenden Fragen:
Um sich den Antworten zu nähern, ist es instruktiv
nochmals die Kepler-Gesetze zu betrachten. Diese beschreiben
geschlossene Planetenbahnen, wenn das Potential sich wie
1∕r verhält. jede Abweichung des Potentials von einem
 -Gesetz bewirkt eine Perihel-Drehung, also auch dann
wenn mehr als ein Planet um das Zentralgestirn sich
bewegen.
-Gesetz bewirkt eine Perihel-Drehung, also auch dann
wenn mehr als ein Planet um das Zentralgestirn sich
bewegen.
__________________________________________________________________________
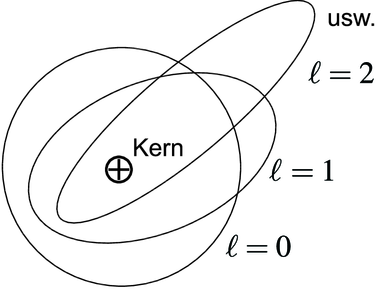
Sommerfeld-Bild: Modell eines Atoms mit einem „Leuchtelektron“
_____________________________________________________________________
Abbildung 6.3.5 zeigt verschiedene Keplerbahnen, wobei die Bahn mit der grössten Exzentrizität die Bahn des Leuchtelektrons sei. Abbildung 6.3.5 zeigt eine Skizze eines Leuchtelektrons auf einer Rydbergbahn zusammen mit dem Kern und der ihn abschirmenden Elektronenwolke
__________________________________________________________________________
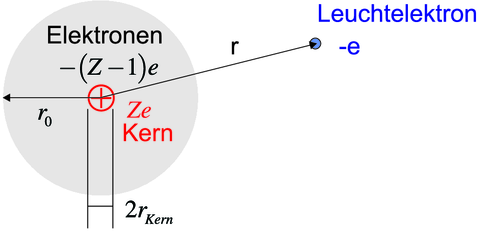
Atom mit einem Leuchtelektron
_____________________________________________________________________
Bei Atomen mit einem Elektron auf einer Rydbergbahn,
wenn also r »r0 gilt, ist die Coulombkraft Fc = −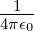
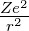 unabhängig von der inneren Struktur des Atoms. Andererseits
ist auch ganz in der Nähe des Kernes, das heisst für
r ≈rKern, die Coulombkraft einfach. Sie muss Fc = −
unabhängig von der inneren Struktur des Atoms. Andererseits
ist auch ganz in der Nähe des Kernes, das heisst für
r ≈rKern, die Coulombkraft einfach. Sie muss Fc = −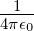
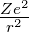 sein.
sein.
__________________________________________________________________________
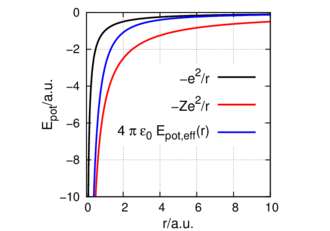
Skizze: Coulombpotential und effektives Potential
_____________________________________________________________________
Abbildung 6.3.5 zeigt eine Skizze des Übergangs vom geschirmten Potential für ein Elektron für r »r0 zum reinen Coulombpotential eines Kerns mit der Ladung Ze. Die genaue Form des effektiven Potentials ist schwierig.
Die Existenz eines effektiven Potentials bedeutet, dass ein Elektron innen sich auf einer Bahn zu einem anderen Coulombpotential als aussen bewegt. Die Energie hängt also nun vom Drehimpuls ab. ℓ = 0 ist eine Kreisbahn, die von einer einzigen effektiven Ladung bestimmt ist., ℓ > 0 bedeutet, dass das Elektron sich in Potentialen zu verschiedenen Energien aufhält. Damit ändert sich die Energie und die Abschirmung hebt die Energieentartung auf.
__________________________________________________________________________
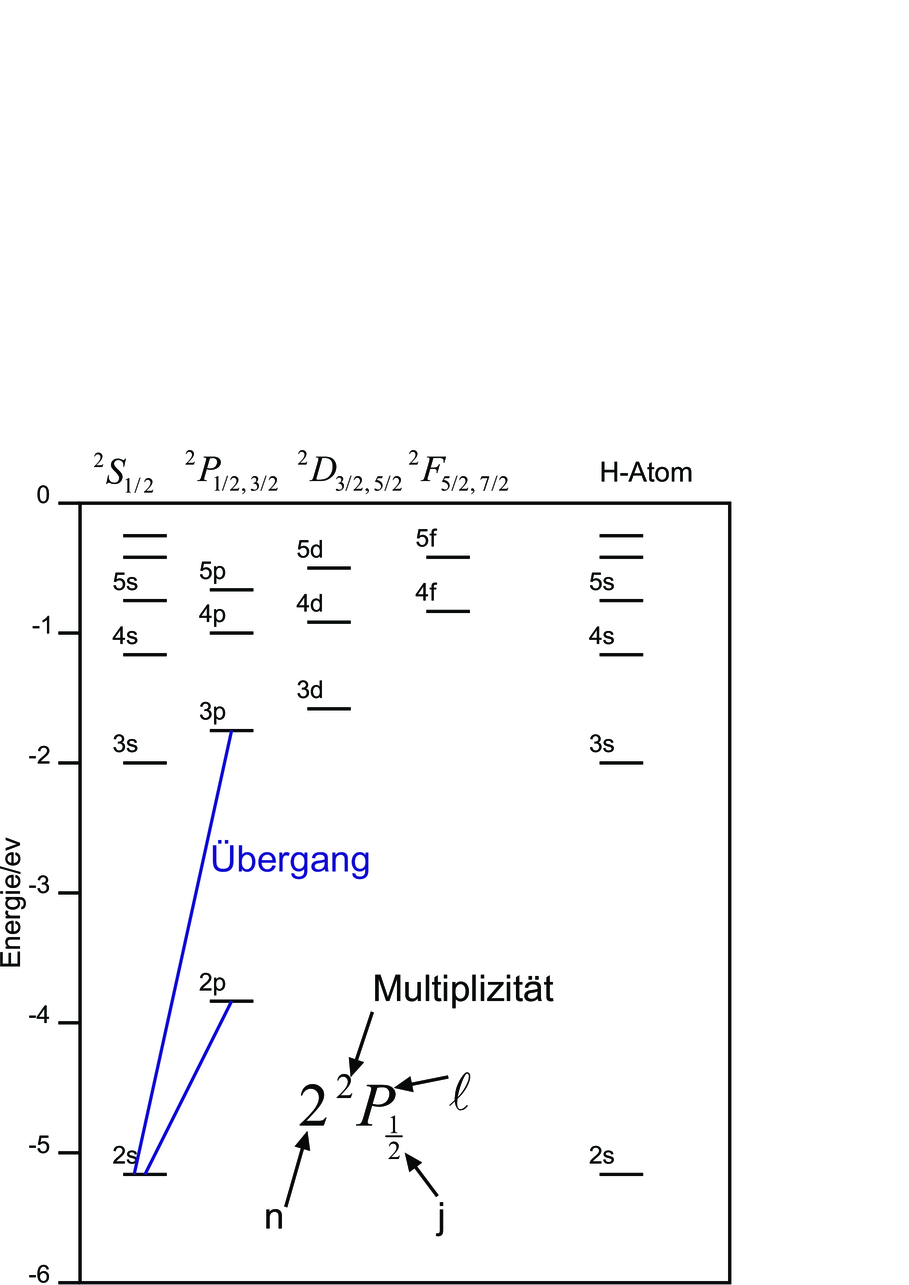
Grotrian-Diagramm für Lithium
_____________________________________________________________________
Energieniveaus werden üblicherweise mit Grotrian-Diagrammen (siehe Abbildung 6.3.5) dargestellt. Die Bedeutung der Symbole ist in Tabelle 6.3.5 zusammengefasst.
___________________________________________________________________________
| Buchstabe | Drehimpuls | Name |
| s | ℓ = 0 | sharp |
| p | ℓ = 1 | principal |
| d | ℓ = 2 | diffuse |
| f | ℓ = 3 | fundamental |
| g | ℓ = 4 |  |
_____________________________________________________________________
Es gibt die folgende Konvention:
Bei den Alkaliatomen kann man empirisch Serienformeln angeben, die analog zur Balmerserie sind. Für die Energien der einzelnen Zustände gilt:
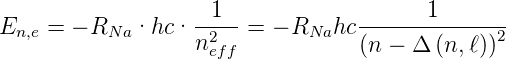 | (6.129) |
neff = n − Δ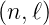 ist dabei eine im Allgemeinen nicht
ganzzahlige Hauptquantenzahl. Δ(n,ℓ) ist der zu n und ℓ
gehörende .
ist dabei eine im Allgemeinen nicht
ganzzahlige Hauptquantenzahl. Δ(n,ℓ) ist der zu n und ℓ
gehörende .
Die Quantenzustände werden als Absorptions- oder Emissionslinien untersucht. Bei Absorptionslinien ist unter Normalbedingungen nur der Grunzustand eines Atoms besetzt: man beobachtet also ausschliesslich die nur die Hauptserie aus Resonanzlinien. Die gelbe D-Linie des Natriumatoms wird durch den Übergang 3s → 3p erzeugt. Die mit Grossbuchstaben bezeichnete Gesamtheit aller s- beziehungsweise p-Terme ist beim Natrium
___________________________________________________________________________
| Hauptserie | 3S ↔nP | |
| Nebenserien | 3P ↔nS | |
| 3P ↔ nD | mit n ≥ 3 | |
___________________________________________________________________________
Beim K-Atom ist die Elektronenkonfiguration der inneren Elektronen eine Ar-Konfiguration. Dazu kommt ein äusseres Leuchtelektron. Die Konfiguration des K-Atoms besteht aus zwei s-Elektronen mit n = 1, bezeichnet als 1s2. Dann folgen zwei s-Elektronen mit n = 2, die mit 2s2 angegeben werden. Weiter gibt es sechs p-Elektronen (2p6) mit n = 2, zwei s-Elektronen mit n = 3, also 3s2 und sechs p-Elektronen mit n = 3 angegeben mit 3p6. Kurz gibt man das als
![1s2 2s2 2p6 3s2 3p6 = ⇒ [Ar ]](ap-2015921x.png) | (6.130) |
In der ganzen Konfiguration ist neben der [Ar]-Edelgaskonfiguration noch ein Elektron unberücksichtigt. Dieses könnte sich sowohl in einem [Ar]3d1 oder [Ar]4s1 sein. Welche Konfiguration hat die kleinste Gesamtenergie? Das s-Elektron hat eine höhere Wahrscheinlichkeit, sich nahe am Kern aufzuhalten als das d-Elektron. Es bewegt sich also mehr im unabgeschirmten, potentialmässig tiefer liegenden Teil des Wechselwirkungspotentials, liegt also bei einer tieferen Energie (siehe auch Abbildung 6.3.5). Obwohl das d-Elektron eine stabilere Konfiguration zu haben scheint, ist die Konfiguration des K [Ar]4s1.
__________________________________________________________________________
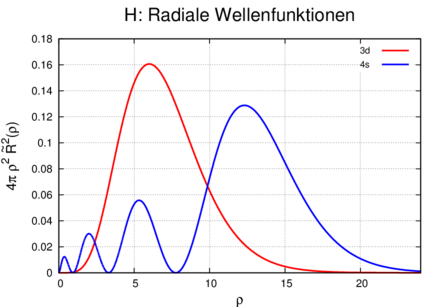
Radiale Wellenfunktionen des Wasserstoffatoms gewichtet mit der Oberfläche der kugelschale beim Radius ρ.
_____________________________________________________________________
Die Wahrscheinlichkeitsdichte berechnet aus der Wellenfunktion gibt die Aufenthaltswahrscheinlichkeit in den drei Dimensionen des Raumes. Nach Einstein und seinen Relativitätstheorien kommt dazu als vierte Dimension die Zeit. Die Zustände eines Elektrons im Wasserstoffatom sind weiter durch die Energie charakterisiert, also eine fünfte Dimension, aber mit diskreten Werten. Im gleiche Sinne stellt die Länge des Bahndrehimpuls eine sechste Dimension, die z-Komponente eine 7. Dimension mit diskreten Werten und die z-Komponente des Spins die 8. Dimension.
Diese Überlegungen sind äquivalenbt zu denen in der theoretischen Mechanik oder der Thermodynamik, wo ein Massenpunkt durch sechs Koordinaten in einem sechsdimensionalen Raum beschrieben werden, durch drei Orts- und drei Impulskoordinaten.
| Wenn nun ein Elektron in einem Atom von einem Zustand einer Energie in einen Zustand einer anderen Energie übergeht, ändert sich sein Ort nicht. |
________________________________________________________________
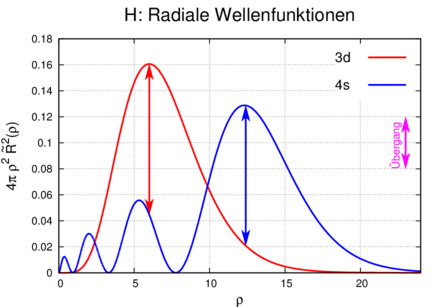
Übergänge zwischen Zuständen am Beispiel der radialen Wellenfunktionen des Wasserstoffatoms gewichtet mit der Oberfläche der Kugelschale beim Radius ρ.
_____________________________________________________________________
Abbildung 6.3.6 zeigt eine Skizze dieses Vorganges. In der Abbildung sind diskrete Linien eingezeichnet. Diese sollen das Franck-Condon-Prinzip, das insbesondere auch für Moleküle gilt, verdeutlichen.
Wie immer in der Quantenmechanik sollten wir mit Wahrscheinlichkeiten argumentieren. Zum Beispiel gibt die blaue Linie in 6.3.6 die Wahrscheinlichkeitsdichte für den 4s-Zustand. Die rote Linie ist die entsprechende Zustandsdichte für den 3d-Zustand.
Die Wahrscheinlichkeit eines Überganges ist das Produkt der Wahrscheinlichkeit des Ausgangszustandes und der Wahrscheinlichkeit des Endzustandes. Wenn Sie in einem Saal den Platz wechseln wollen, benötigen Sie einen freien Stuhl als Ziel.
Um die Wahrscheinlichkeit des Überganges aus dem Zustand x in den Zustand y zu berechnen, müssen die Übergangmatrixelemente berechnet werden, also
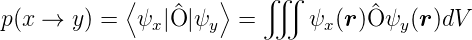 | (6.131) |
Dabei ist 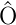 der Operator, der den Übergang beschreibt, also
zum Beispiel ein Dipoloperator oder ein Quadrupoloperator.
der Operator, der den Übergang beschreibt, also
zum Beispiel ein Dipoloperator oder ein Quadrupoloperator.
Durch die Emission des Photons (oder auch durch seine Absorption) bekommt das Atom einen Impuls (Rückstoss). Aber: Im Augenblick des Überganges bleibt das Elektron beschrieben durch seine Wellenfunktion am Ort.
Oftmals werden wegen der Übersichtlichkeit Übergänge örtlich schräg gezeichnet, zum Beispiel in Grotrian-Diagrammen (siehe zum Beispiel Abbildung 6.3.5). Lassen Sie sich dadurch nicht verwirren!
 Lizenzinformationen
Lizenzinformationen