| Radiale
Wellenfunktion n = 1 ℓ = 0 ⇒ 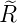 1,0(ϱ) = 1,0(ϱ) =
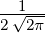 e−ϱ∕2 e−ϱ∕2 | 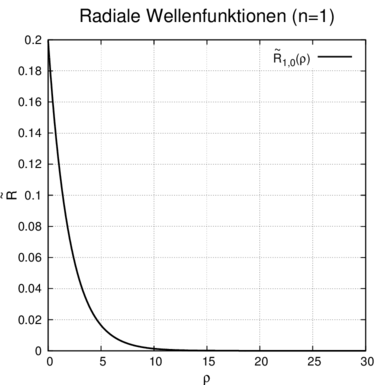 |
| Radiale
Wellenfunktion n = 2 ℓ = 0 ⇒ 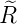 2,0(ϱ) = 2,0(ϱ) =
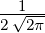 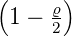 e−ϱ∕2 e−ϱ∕2 ℓ = 1 ⇒ 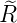 2,1(ϱ) = 2,1(ϱ) =
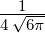 ϱe−ϱ∕2 ϱe−ϱ∕2 | 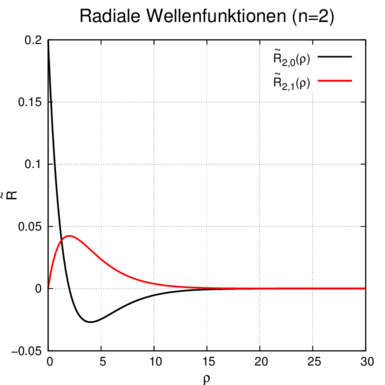 |
| Radiale
Wellenfunktion n = 3 ℓ = 0 ⇒ 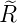 3,0(ϱ) = 3,0(ϱ) =
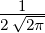 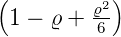 e−ϱ∕2 e−ϱ∕2
ℓ = 1 ⇒ 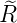 3,1(ϱ) = 3,1(ϱ) =
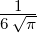 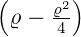 e−ϱ∕2 e−ϱ∕2 ℓ = 2 ⇒ 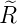 3,2(ϱ) = 3,2(ϱ) =
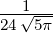 ϱ2e−ϱ∕2 ϱ2e−ϱ∕2 | 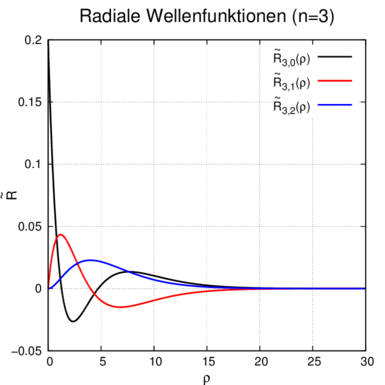 |
| Radiale
Wellenfunktion n = 4 ℓ = 0 ⇒ 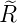 4,0(ϱ) = 4,0(ϱ) =
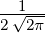 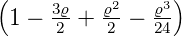 e−ϱ∕2 e−ϱ∕2
ℓ = 1 ⇒ 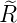 4,1(ϱ) = 4,1(ϱ) =
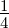 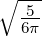 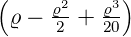 e−ϱ∕2 e−ϱ∕2
ℓ = 2 ⇒ 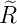 4,2(ϱ) = 4,2(ϱ) =
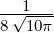 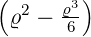 e−ϱ∕2 e−ϱ∕2 ℓ = 3 ⇒ 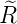 4,3(ϱ) = 4,3(ϱ) =
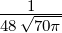 ϱ3e−ϱ∕2 ϱ3e−ϱ∕2 | 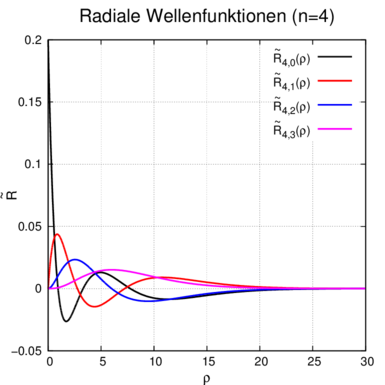 |
| Radiale
Wellenfunktion n = 5 ℓ = 0 ⇒ 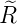 5,0(ϱ) = 5,0(ϱ) =
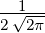 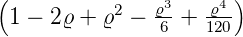 e−ϱ∕2 e−ϱ∕2
ℓ = 1 ⇒ 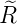 5,1(ϱ) = 5,1(ϱ) =
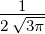 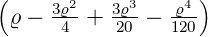 e−ϱ∕2 e−ϱ∕2
ℓ = 2 ⇒ 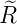 5,2(ϱ) = 5,2(ϱ) =
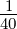 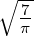 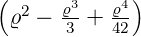 e−ϱ∕2 e−ϱ∕2
ℓ = 3 ⇒ 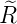 5,3(ϱ) = 5,3(ϱ) =
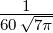 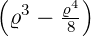 e−ϱ∕2 e−ϱ∕2 ℓ = 4 ⇒ 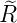 5,4(ϱ) = 5,4(ϱ) =
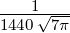 ϱ4e−ϱ∕2 ϱ4e−ϱ∕2 | 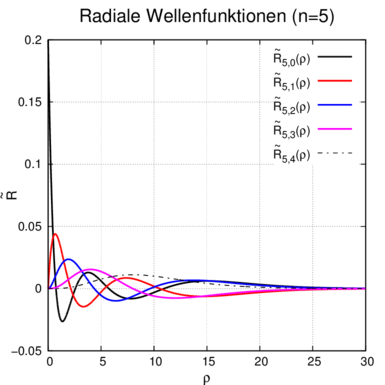 |

 Lizenzinformationen
Lizenzinformationen