__________________________________________________________________________
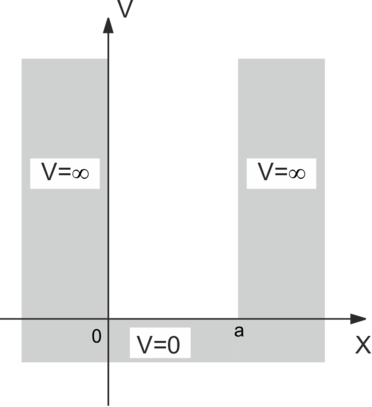
Potentialtopf mit unendlich hohen Wänden.
_____________________________________________________________________

__________________________________________________________________________

Potentialtopf mit unendlich hohen Wänden.
_____________________________________________________________________
Die zeitunabhängige Schrödingergleichung erlaubt die Berechnung der Wellenfunktion eines Teilchens in einem unendlichen tiefen Potentialtopf (Abb. 5.7). Die Breite des Topfes ist a. Wir nehmen als Ansatz die Funktion ψ(x,t) = ϕ(x)e−iωt. Die zeitunabhängige Schrödingergleichung lautet
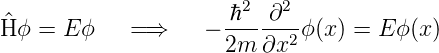 | (5.1) |
Dabei haben wir die Potentialfunktion
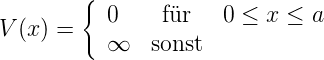 | (5.2) |
Im Potentialtopf für 0 ≤ x ≤ a haben die Lösungen die Form
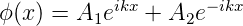 | (5.3) |
mit k = 2π∕λ. Die beide Terme entsprechen zwei harmonischen Wellen, die sich in der negativen und der positiven Richtung der x-Achse ausbreiten. Die Potentialfunktion V in den Wänden des Potentialtopfs hat den Wert unendlich. Dann sind die Amplituden der Lösungen der Schrödingergleichung innerhalb der Wände des Topfes null. Mit anderen Worten, die Wellenfunktion soll für ϕ(x ≤ 0) = 0 und ϕ(x ≥ a) = 0 verschwinden. Die Randbedingungen ergeben
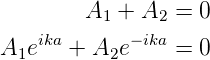 | (5.4) |
Wenn wir die obigen Gleichungen nach A1 und A2 auflösen, bekommen wir
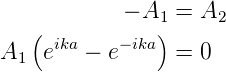 | (5.5) |
Nun ist eika − e−ika = 2i sin 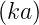 . Wir erhalten also
. Wir erhalten also
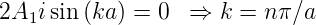 | (5.6) |
mit n ∈ ℤ. Die Lösung der Schrödingergleichung für den Potentialtopf hat also die Form
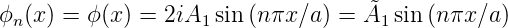 | (5.7) |
Wenn wir den Ansatz unter Berücksichtigung der Randbedingungen in die Schrödingergleichung (5.1) einsetzen
können die dazugehörigen Energieeigenwerte gefunden werden
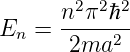 | (5.9) |
Die Wellenfunktion ϕn(x) muss auf 1 normiert sein, da
wir das Teilchen sicher im gesamten Raum finden. Aus
∫
0aϕ∗
n(x)·ϕn(x)dx = 1 erhalten wir den Wert der Konstanten
Ã1 = 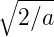 oder A1 =
oder A1 = 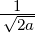 .
.
| Die Einschränkung (Lokalisierung) der Wellenfunktion auf ein beschränktes Gebiet, den Potentialkasten, bedingt die Quantisierung der Teilchenenergie. |
 Lizenzinformationen
Lizenzinformationen