Weiter: Abbildungsverzeichnis Oben: Vorlesungsskript PHYS 70357 Elektrizitätslehre Zurück: Versuche Skript: PDF-Datei Übungen: Blätter
Die Korrekturen hier sind in dieser aktuellen Version ausgeführt. Wenn Sie eine Version vom 1. 10. 2004 haben, sind unten die richtigen Gleichungen angegeben. Sollten Sie einen älteren Ausdruck haben, übernehmen Sie bitte die Daten.
![[*]](crossref.gif) , Gleichung (2.75):
, Gleichung (2.75):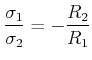 |
![[*]](crossref.gif) , Abschnitt 12:
, Abschnitt 12: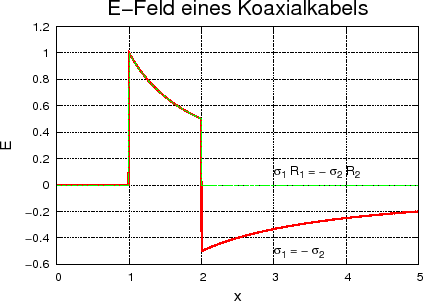 |
||||
 |
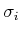 |
|||
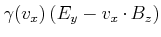 |
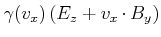 |
![[*]](crossref.gif) , Abschnitt 2.8.1:
, Abschnitt 2.8.1:
![\includegraphics[width=0.5\textwidth]{elektrostatik-035}](img387.gif)
Schematische Darstellung des Flächenladungsversuches.
|
In der Abbildung 2.28 wird der Messprozess schematisch gezeigt. Eine Kugel mit dem Radius ![]() wird auf die Spannung
wird auf die Spannung ![]() aufgeladen. Die kleine Kugel mit dem Radius
aufgeladen. Die kleine Kugel mit dem Radius ![]() wird mit der grossen Kugel in Kontakt gebracht. Nach kurzer Zeit haben beide Kugeln gegen Erde (unendlich) das Potential
wird mit der grossen Kugel in Kontakt gebracht. Nach kurzer Zeit haben beide Kugeln gegen Erde (unendlich) das Potential
![]() . Wenn wir annehmen, dass die kleine Kugel eine unwesentliche Störung der grossen Kugel ist, ist die Kapazität der beiden Kugeln
. Wenn wir annehmen, dass die kleine Kugel eine unwesentliche Störung der grossen Kugel ist, ist die Kapazität der beiden Kugeln
Die Flächenladungsdichte der beiden Kugeln im Kontakt ist durch
Die Kugel hat nach der Trennung ein anderes Potential gegen unendlich, nämlich
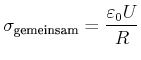
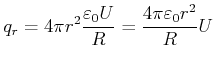 |
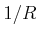 |
Aus Gleichung (2.105) und Gleichung (2.106) erhalten wir
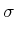 |
Die Kugel wird schliesslich auf das Ladungsmessgerät (eigentlich ein Strom-Integrierer) aufgebracht. Die gemessene Ladung ist proportional zu ![]() und damit proportional zu
und damit proportional zu
![]() gemeinsam.
gemeinsam.
![[*]](crossref.gif) , Gleichung (3.98):
, Gleichung (3.98):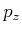 |
|||
![[*]](crossref.gif) , Gleichung (3.102):
, Gleichung (3.102):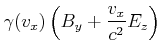 |
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2:
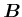 |
![[*]](crossref.gif) , Abschnitt 28:
, Abschnitt 28: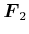
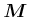
![[*]](crossref.gif) , Abschnitt 13:
, Abschnitt 13:Das Vektorpotential
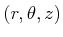
ergibt das magnetische Feld für einen in der ![]() -Richtung laufenden Strom
-Richtung laufenden Strom ![]()
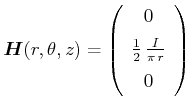
In Zylinderkoordinaten
![]() gehört zum Magnetfeld
gehört zum Magnetfeld
das Vektorpotential
![[*]](crossref.gif) , Gleichung (2.53):
, Gleichung (2.53): |
![[*]](crossref.gif) , Gleichung (3.145):
, Gleichung (3.145):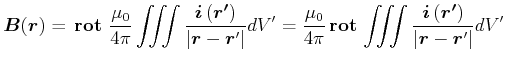 |
![[*]](crossref.gif) , Abschnitt 13:
, Abschnitt 13: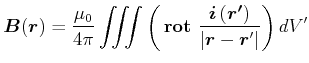 |
Nun bezieht sich die Rotation nur auf ![]() , nicht aber auf
, nicht aber auf ![]() . Deshalb kann sie unter das Integral gezogen werden.
. Deshalb kann sie unter das Integral gezogen werden.
 |
Nun gilt für die Rotation eines Produktes (Siehe Bronstein, Taschenbuch der Mathematik [BSMM00, pp. 468])
Hier ist der Vektor
![]() bezüglich der Rotation eine Konstante, da er nur von
bezüglich der Rotation eine Konstante, da er nur von ![]() und nicht von
und nicht von ![]() abhängt. Weiter darf die Ableitung irgend eines Punktes nicht davon abhängen dass das Koordinatensystem um einen Konstanten Vektor verschoben wurde. Wir rechnen deshalb die Ableitungen in der Rotation, beziehungsweise im Gradienten, nicht bezüglich
abhängt. Weiter darf die Ableitung irgend eines Punktes nicht davon abhängen dass das Koordinatensystem um einen Konstanten Vektor verschoben wurde. Wir rechnen deshalb die Ableitungen in der Rotation, beziehungsweise im Gradienten, nicht bezüglich ![]() sondern bezüglich des verschobenen Koordinatensystems
sondern bezüglich des verschobenen Koordinatensystems
![]() aus. Es bleibt also
aus. Es bleibt also
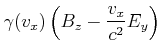 |
||
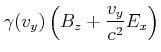 |
||
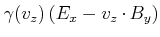 |
||
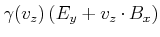 |
||
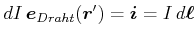 |
Wir betrachten nun einen infinitesimal dünnen Strom
![]() .
.
![]() ist ein Einheitsvektor entlang des Drahtes. Da
ist ein Einheitsvektor entlang des Drahtes. Da ![]() überall null ist ausser auf dem eindimensionalen Draht, wird aus dem Volumenintegral ein eindimensionales Integral. Wieder ist es für die Integration egal, ob wir
überall null ist ausser auf dem eindimensionalen Draht, wird aus dem Volumenintegral ein eindimensionales Integral. Wieder ist es für die Integration egal, ob wir ![]() von
von ![]() oder von
oder von
![]() abhängen lassen.
abhängen lassen.
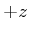 |
Diese Gleichung ist bekannt als das Gesetz von Biot-Savart. Mit ihm kann man das Feld einer beliebigen Leiteranordnung berechnen.
Auch wenn sie physikalisch keine Bedeutung hat, kann es sinnvoll sein in Zwischenschritten die differentielle Formulierung zu verwenden, nämlich die Formel von Laplace.
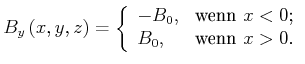 |
![[*]](crossref.gif) , Gleichung (3.178):
, Gleichung (3.178):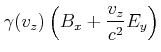 |
||
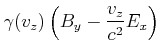 |
||
![[*]](crossref.gif) , Gleichung (4.18):
, Gleichung (4.18):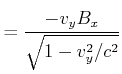 |
|||||
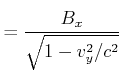 |
![[*]](crossref.gif) , Abschnitt 4.1.5:
, Abschnitt 4.1.5:
Da ![]() konstant ist, schreiben wir
konstant ist, schreiben wir ![]() und
und ![]() als Funktion des Winkels
als Funktion des Winkels ![]()
Der Strom ![]() soll im Gegenuhrzeigersinn umlaufen, also in positiver Richtung. Ein Längenelement entlang des Kreisringes ist
soll im Gegenuhrzeigersinn umlaufen, also in positiver Richtung. Ein Längenelement entlang des Kreisringes ist
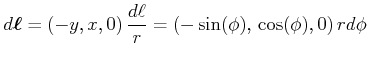
Das Vektorprodukt
![]() ergibt
ergibt
![[*]](crossref.gif) , Gleichung (5.13):
, Gleichung (5.13): |
|||
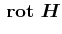 |
![[*]](crossref.gif) , Gleichung (5.14):
, Gleichung (5.14):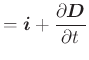 |
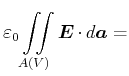 |
||
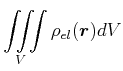 |
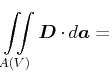 |
||
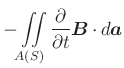 |
|||
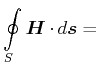 |
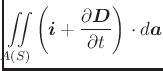 |
![[*]](crossref.gif) , Gleichung (6.63):
, Gleichung (6.63):![[*]](crossref.gif) , Gleichung (6.64):
, Gleichung (6.64):![[*]](crossref.gif) , Gleichung (6.65):
, Gleichung (6.65):![[*]](crossref.gif) , Gleichung (6.75):
, Gleichung (6.75):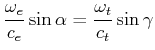 |
![[*]](crossref.gif) , Gleichung (6.79):
, Gleichung (6.79):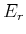 |
![[*]](crossref.gif) , Abschnitt 6.7.2:
, Abschnitt 6.7.2:
![\includegraphics[width=0.9\textwidth]{em-wellen-010}](img1922.gif)
Darstellung der Richtungen der elektrischen Felder für die
|
Im Grenzfall
![]() müssen die Resultate für die
müssen die Resultate für die ![]() - und
- und ![]() -Polarisation übereinstimmen. Lässt man in Gleichung (6.99)
-Polarisation übereinstimmen. Lässt man in Gleichung (6.99) ![]() gegen null gehen, ergibt sich für das reflektierte elektrische Feld
gegen null gehen, ergibt sich für das reflektierte elektrische Feld ![]() . Andererseits ist der Grenzwert des elektrischen Feldes
. Andererseits ist der Grenzwert des elektrischen Feldes ![]() für
für ![]() gegen Null bei Gleichung (6.87) negativ. Dies ist korrekt, da nach der Abbildung 6.16 die Vektoren für beide Polarisationen in unterschiedliche Richtungen zeigen. Die beiden Werte
gegen Null bei Gleichung (6.87) negativ. Dies ist korrekt, da nach der Abbildung 6.16 die Vektoren für beide Polarisationen in unterschiedliche Richtungen zeigen. Die beiden Werte ![]() und
und ![]() sind die Vorfaktoren. Also zeigen die beiden elektrischen Felder der reflektierten Wellen identisch.
sind die Vorfaktoren. Also zeigen die beiden elektrischen Felder der reflektierten Wellen identisch.
Wenn in der Gleichung Gleichung (6.99) für ![]() der Nenner
der Nenner
![]() ist, divergiert der Nenner, Wir erhalten also
ist, divergiert der Nenner, Wir erhalten also
![]() . Dies ist der Brewster-Winkel.
. Dies ist der Brewster-Winkel.
![[*]](crossref.gif) , Abschnitt 13:
, Abschnitt 13:
Othmar Marti