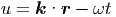

Es gibt eine grosse Klasse von Funktionen (skalar oder vektoriell), die die Wellenleitergleichung lösen. Im Folgenden besprechen wir skalare Funktionen, die aber auch als eine Vektorkomponente aufgefasst werden können. Alle Funktionen, die nur von einer skalaren Variablen
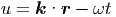 | (6.1) |
abhängen lösen die Wellengleichung, wenn sie
genügend oft stetig differenzierbar sind. Wir betrachten
die Funktion f(u) = f(u(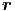 ,t)). und setzen sie in
c2Δf(u(
,t)). und setzen sie in
c2Δf(u(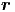 ,t)) = (∂2∕∂t2)f(u(
,t)) = (∂2∕∂t2)f(u(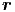 ,t)) ein. Die Kettenregel der
Differentiation ergibt für u =
,t)) ein. Die Kettenregel der
Differentiation ergibt für u =  ·
·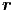 −ωt = kxx + kyy + kzz −ωt
−ωt = kxx + kyy + kzz −ωt
Die letzte Umformung in Gleichung (6.3) beruht auf
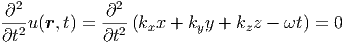 |
Da (∂∕∂t)u = −ω ist, ist auch
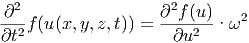 | (6.4) |
Analog erhalten wir für die Raumkomponente x
Also ist wieder mit 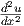 = 0 und zyklisch für x,y,z
= 0 und zyklisch für x,y,z
Damit lautet die Wellengleichung mit Gleichung (6.3), Gleichung (6.6), Gleichung (6.4) und Gleichung (6.7)
Damit können wir sagen:
Jede Funktion  (u) mit u = (u) mit u = 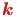 · · − ωt ist eine
Lösung der Wellengleichung − ωt ist eine
Lösung der Wellengleichung
sofern
gilt. |
Aus den Gleichungen (6.3) kann die Orientierung von 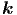 ,
, 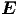 und
und 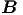 berechnet werden. Wir verwenden die Gleichungen
(6.9) und (6.10) und schreiben alle Ableitungen nach x, y, z
und t als Kettenableitungen zuerst nach u. Wenn
berechnet werden. Wir verwenden die Gleichungen
(6.9) und (6.10) und schreiben alle Ableitungen nach x, y, z
und t als Kettenableitungen zuerst nach u. Wenn 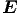 (u) aus
der Wellengleichung bekannt ist, verwenden wir die II.
Maxwellgleichung aus (6.3) und erhalten
(u) aus
der Wellengleichung bekannt ist, verwenden wir die II.
Maxwellgleichung aus (6.3) und erhalten
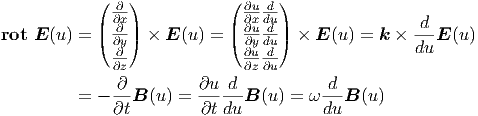
Wir haben dabei verwendet, dass du∕dx = kx,
du∕dy = ky, du∕dz = kz und du∕dt = −ω. Damit ist auch
(du∕dx,du∕dz,du∕dz)T = (k
x,ky,kz)T = 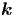 . Integrieren wir
die Gleichung (6.11) nach u erhalten wir
. Integrieren wir
die Gleichung (6.11) nach u erhalten wir
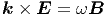 | (6.12) |
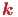 , ,  und und  bilden in dieser Reihenfolge ein
rechtshändiges Dreibein. Die drei Vektoren stehen
paarweise rechtwinklig aufeinander. bilden in dieser Reihenfolge ein
rechtshändiges Dreibein. Die drei Vektoren stehen
paarweise rechtwinklig aufeinander. |
Hätten wir die die Wellengleichung für 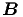 gelöst, hätten wir
die Beziehung
gelöst, hätten wir
die Beziehung
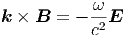 | (6.13) |
bekommen. Diese Beziehung (6.13) ist aber unter Verwendung von (6.10) identisch mit (6.12).
Betragsmässig haben wir im Vakuum weiter die Beziehung
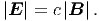 | (6.14) |
 Lizenzinformationen
Lizenzinformationen