Fraunhofersche und Fresnelsche Beugung

(Siehe Hecht, Optik [Hec, pp. 650, 710]) (Siehe Tipler, Physik [TM04, pp. 1131]) (Siehe Sommerfeld, Theoretische Physik Band IV, Optik [Som78, pp. 206])

Berechnung der Fresnelbeugung an einer Halbebene.

Bei der Beugung interferiert Licht von Kugelwellen aus allen Punkten mit den Koordinaten $x'$ im Beobachtungspunkt mit der Koordinate $x$. Für eine einzelne Teilwelle ist der Weg

$$s = \sqrt{D^2+(x-x')^2}$$ (5..91)

Entsprechend ist die komplexe Amplitude am Punkt $x$ gegeben durch

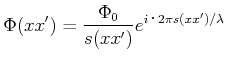$$\Phi(x,x') = \frac{\Phi_0}{s(x,x')}e^{i\cdot 2\pi s(x,x')/\lambda}$$ (5..92)

Die Amplitude am Punkt $x$ ist dann nach Huygens

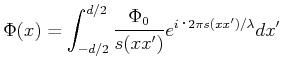$$\Phi(x) = \int_{-d/2}^{d/2} \frac{\Phi_0}{s(x,x')}e^{i\cdot 2\pi s(x,x')/\lambda} dx'$$ (5..93)

da wir Kugelwellen haben. Diese Gleichung kann numerisch gelöst werden. Es existieren die folgenden Näherungen:

Fresnelsche Näherung

(Siehe Hecht, Optik [Hec, pp. 710]) (Siehe Sommerfeld, Theoretische Physik Band IV, Optik [Som78, pp. 206])

Wir betrachten nur Orte, bei denen $\vert x-x'\vert \ll D$ sind. Dann ist

$$s \approx D + \frac{(x-x')^2}{2D}$$ (5..94)

und $1/s \approx 1/D$. Das heisst auch, dass die Phase ist proportional zu $(x-x')^2$. Unser Integral wird dann

$$\Phi(x) = \frac{\Phi_0}{D}\int_{-d/2}^{d/2} e^{i \cdot 2 \pi s(x,... ... = \frac{\Phi_0}{D}\int_{-d/2}^{d/2} e^{i\cdot 2\pi[D+ (x'-x)^2/2D]\lambda} dx'$$ (5..95)

und

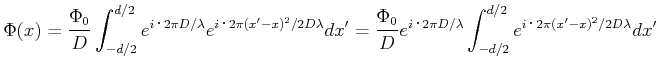$$\Phi(x) = \frac{\Phi_0}{D}\int_{-d/2}^{d/2} e^{i\cdot 2\pi D/\lam... ...^{i\cdot 2\pi D/\lambda}\int_{-d/2}^{d/2} e^{i\cdot 2\pi(x'-x)^2/2D\lambda} dx'$$ (5..96)

Mit der Variablentransformation $\xi = x'-x$ und damit den Grenzen $\xi_u = -d/2-x$ und $\xi_o=d/2-x$ wird das Integral zu

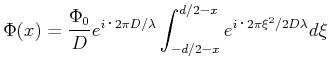$$\Phi(x) = \frac{\Phi_0}{D}e^{i\cdot 2\pi D/\lambda}\int_{-d/2-x}^{d/2-x} e^{i\cdot 2\pi\xi^2/2D\lambda} d\xi$$ (5..97)

Das verbleibende Integral $\int_{-d/2-x}^{d/2-x} e^{i\cdot 2\pi\xi^2/2D\lambda} d\xi$ kann als Summe und Differenz der Fresnelschen Integrale geschrieben werden. Wir verwenden, dass $e^{i\alpha} = \cos\alpha + i\sin\alpha$ ist.

Dieses Integral, nach Real- und Imaginärteil aufgetrennt und normiert ergibt die Fresnelschen Integrale

$$C(w) = \int_0^w \cos\left(\frac{\pi}{2}\tau^2\right) d\tau$$

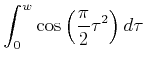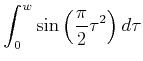$$S(w) = \int_0^w \sin\left(\frac{\pi}{2}\tau^2\right) d\tau$$ (5..98)

Die Funktion $\Phi(x)$ kann als Differenz zweier Fresnelscher Integrale geschrieben werden

$$\Phi(x) = K \left[C\left((d/2-x)\cdot k\right)-C\left((-d/2-x)\cdot k\right)\right]$$

$$ +i\cdot K \left[S\left((d/2-x)\cdot k\right)-S\left((-d/2-x)\cdot k\right)\right]$$ (5..99)

wobei $K$ eine von der Intensität abhängige Konstante ist.

Die Cornu-Spirale. Aufgetragen ist die parametrische Kurve $(C(w),S(w))$ mit $-\infty \leq w \leq \infty$. Die linke untere Spirale entspricht $w=-\infty$, die rechte obere Spirale $w=\infty$.

Die durch $F(w) = C(w) + iS(w)$ definierte Ortskurve ist die Cornu-Spirale. Dies e-Funktion beschreibt eine längentreue Abbildung der reellen Achse $w$ auf die komplexe $C,S$-Ebene. Mit dieser Konstruktion kann auf einfachem graphischem Wege das Beugungsmuster konstruiert werden. Dazu zeichnet man vom Ortspunkt der unteren Integrationsgrenze zum Ortspunkt der oberen Integrationsgrenze eine Linie. Deren Länge gibt die Amplitude, deren Winkel zur reellen Achse die Phase. Damit kann das Fresnel-Beugungsbild eines Spalts berechnet werden.

Fresnelsches Beugungsmuster an einem Spalt der Breite 1. Links die Amplitude und rechts die Intensität.

Wenn man die untere Integrationsgrenze nach $-\infty$ gehen lässt und bei der oberen Integrationsgrenze $d$ gegen Null gehen lässt, bekommt man das Beugungsbild an einer Kante. Wir tragen nun die Strecke vom Zentrum der linken Spirale ( $F(-\infty) = -1/2 ( 1+i)$) aus zum Ortspunkt korrespondierend zu $x$ ab. Wir sehen, dass im Schattenbereich (bis der bewegliche Ortspunkt $0,0$ erreicht) die Amplitude monoton zunimmt. Dann beginnt eine Oszillation, die als die Interferenzmuster im hellen Bereich beobachtet werden kann.

Fresnelsches Beugungsmuster an einer Halbebene. Links die Amplitude und rechts die Intensität.

Fraunhofer-Beugung

Die Gleichung (5.94) kann weiter vereinfacht werden, wenn $\vert x'\vert \ll \vert x\vert$ ist. Dann bekommen wir

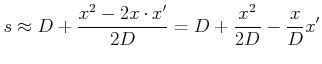$$s \approx D +\frac{x^2 -2 x\cdot x'}{2D} = D + \frac{x^2}{2D} - \frac{x}{D} x'$$ (5..100)

Nun ist die optische Distanz $s$ eine lineare Funktion von $x'$. Die Approximation gilt nur, wenn das Beugungsobjekt klein gegen die Distanz zum Objekt und der Grösse des Beugungsmusters ist. Diese Fernfeld-Approximation nennt man die Fraunhofer-Näherung.

Vergleich

(Siehe Pérez, Optik [Pér96, pp. 327])

Die bis jetzt besprochenen Beugungseffekte haben die folgenden Eigenschaften:

Fraunhofersche Beugung

1. Ebene Wellen fallen so auf einen Spalt, dass ihre Strahlen senkrecht auf ihn treffen. Damit sind die Amplituden und die Phasen der nach dem Huygensschen Prinzip emittierten Wellen gleich.
2. Das Beugungsbild wird auf einem weit entfernten Schirm beobachtet. Die von Punktquellen ausgehenden Strahlen treffen ungefähr parallel auf den Schirm.

Ist eine der obigen Bedingungen nicht erfüllt, spricht man von Fresnelscher Beugung. Eine andere Formulierung der Bedingungen der Fraunhoferschen Beugung ist

1. Der Abstand $R$ von der Quelle zum Beugungsobjekt ist sehr viel grösser als die charakteristische Länge $d$ des Beugungsobjekts.
2. Der Abstand $R'$ vom Beobachter zum Beugungsobjekt ist sehr viel grösser als die charakteristische Länge $d$ des Beugungsobjekts.

Vergleich der Fresnelbeugung (rot) mit der Fraunhoferbeugung (schwarz) für Spaltweiten von $0.1$ und $1$.

Vergleich der Fresnelbeugung (rot) mit der Fraunhoferbeugung (schwarz) für Spaltweiten von $2$ und $3$.

Vergleich der Fresnelbeugung (rot) mit der Fraunhoferbeugung (schwarz) für Spaltweiten von $4$ und $5$.