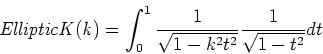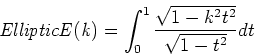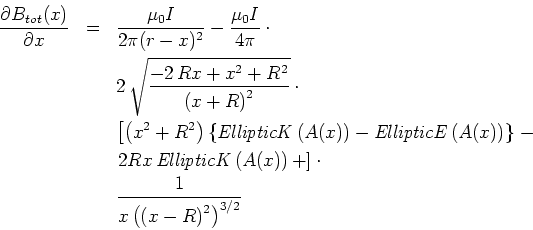

Up: Grundkurs IIIb für Physiker
Übungsblatt 06
Grundkurs IIIb für Physiker
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
20. 1. 2003 oder 27. 1. 2003
Quellenfreiheit, Hall-Effekt,
Lorentztransformation, das Faradaysche Induktionsgesetz,
Energie des Magnetfeldes, PDF-Datei
- Ein Koaxialkabel bestehe aus zwei sehr dünnwandigen Zylindern mit den Radien
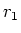 (innen) und
(innen) und 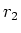 (aussen).
Der Strom
(aussen).
Der Strom 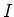 fliesse im inneren Zylinder hin und im äusseren Zylinder zurück.
fliesse im inneren Zylinder hin und im äusseren Zylinder zurück.
![\includegraphics[width=0.3\textwidth]{ue-06-02.eps}](img4.gif)
- verwenden Sie das Ampèresche Gesetz, um
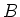 zu berechnen. Zeigen Sie, dass
zu berechnen. Zeigen Sie, dass 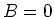 ist,
ausser zwischen den Leitern.
ist,
ausser zwischen den Leitern.
- Zeigen Sie, dass die magnetische Energiedichte zwischen den Zylindern
ist.
- Berechnen Sie die magnetische Energie in einem Zylinderschalen-Volumenelement
der Länge
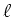 mit dem Volumen
mit dem Volumen
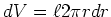 , und zeigen Sie durch Integration, dass
die gesamte magnetische Energie im Volumen der Länge
, und zeigen Sie durch Integration, dass
die gesamte magnetische Energie im Volumen der Länge 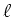
ist.
- Verwenden Sie das Resultat von 1c und die Beziehung
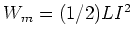 um zu zeigen,
dass die Selbstinduktivität pro Längeneinheit
um zu zeigen,
dass die Selbstinduktivität pro Längeneinheit
ist.
- Die Schaltung
![\includegraphics[width=0.5\textwidth]{ue-06-01.eps}](img13.gif)
habe einen Widerstand von
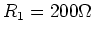 sowie
sowie 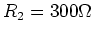 . Wenn der Schalter
. Wenn der Schalter  im Kreis 1
geschlossen wird, fliesst im Kreis 2 die Gesamtladung
im Kreis 1
geschlossen wird, fliesst im Kreis 2 die Gesamtladung
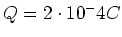 durch das Galvanometer. Nach
langer Zeit betrage die Stromstärke im ersten kreis
durch das Galvanometer. Nach
langer Zeit betrage die Stromstärke im ersten kreis 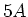 . Berechnen Sie die Gegeninduktivität der beiden
Spulen.
. Berechnen Sie die Gegeninduktivität der beiden
Spulen.
- Der Stab in der Abbildung
![\includegraphics[width=0.5\textwidth]{ue-06-05.eps}](img19.gif)
habe den Widerstand 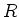 und der Widerstand der Schienen sowie die Kontaktwiderstände seien
vernachlässigbar. An die Punkte
und der Widerstand der Schienen sowie die Kontaktwiderstände seien
vernachlässigbar. An die Punkte 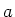 und
und 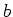 werde eine Spannungsquelle mit vernachlässigbarem
Innenwiderstand so angeschlossen, dass der Strom im Stab nach unten fliesst. Zum Zeitpunkt
werde eine Spannungsquelle mit vernachlässigbarem
Innenwiderstand so angeschlossen, dass der Strom im Stab nach unten fliesst. Zum Zeitpunkt 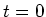 sei
der Stab in Ruhe.
sei
der Stab in Ruhe.
- Bestimmen Sie die Kraft auf den Stab als Funktion der Geschwindigkeit
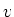 und formulieren Sie das
zweite Newtonsche Gesetz für den Stab, wenn er die Geschwindigkeit
und formulieren Sie das
zweite Newtonsche Gesetz für den Stab, wenn er die Geschwindigkeit 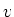 hat.
hat.
- Zeigen Sie, dass der Stab eine endliche Endgeschwindigkeit erreicht, und stellen sie für diese eine
Beziehung auf.
- Wie gross ist die Stromstärke, wenn der Stab seine Endgeschwindigkeit erreicht?
- Magnetfeld einer Leiteranordnung
![\includegraphics[width=0.3\textwidth]{ue-06-03.eps}](img25.gif)
- Bestimmen Sie das Magnetfeld am Punkt
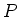 im Abstand
im Abstand 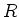 vom stromdurchflossenen Leiter.
vom stromdurchflossenen Leiter.
- Verwenden Sie das Resultat um die Feldstärke in der Mitte eines Polygons mit
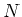 Seiten zu
berechnen.
Seiten zu
berechnen.
- Zeigen Sie, dass für grosse
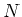 , die Lösung in diejenige für ein Magnetfeld in der Mitte
eines stromdurchflossenen Kreises übergeht.
, die Lösung in diejenige für ein Magnetfeld in der Mitte
eines stromdurchflossenen Kreises übergeht.
- In Elektromotoren schaltet man bisweilen einen Widerstand in Reihe zum Rotor, um den Anfangsstrom zu begrenzen, wenn
der Motor seine Nenndrehzahl noch nicht erreicht hat. Der Widerstand wird abgeschaltet, wenn der Motor
mit normaler Drehzahl läuft.
- Ein Motor habe den Widerstand
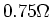 und nehme
und nehme 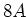 bei
bei 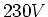 auf. Wie gross muss der
Zusatzwiderstand bemessen sein, damit der Anfangsstrom
auf. Wie gross muss der
Zusatzwiderstand bemessen sein, damit der Anfangsstrom 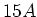 nicht überschreitet?
nicht überschreitet?
- Wie gross ist die Gegeninduktionsspannung, wenn der Motor seine Nenndrehzahl erreicht hat
und der Widerstand abgeschaltet ist?
- Zeigen Sie: Durch eine Spule mit
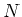 Windungen und dem Widerstand
Windungen und dem Widerstand 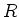 fliesst stets die gesamte Ladung
fliesst stets die gesamte Ladung
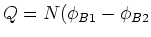 , wenn sich der Fluss von
, wenn sich der Fluss von 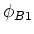 auf
auf 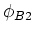 ändert, unabhängig davon
wie dies geschieht.
ändert, unabhängig davon
wie dies geschieht.
- Ein unendlich langer Draht ist wie
![\includegraphics[width=0.3\textwidth]{ue-06-04.eps}](img35.gif)
gebogen. Der ringförmige Teil habe den Radius 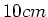 und sei
und sei 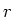 vom geraden Teil entfernt.
vom geraden Teil entfernt.
- Wie gross muss
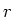 , so dass im Kreismittelpunkt das Magnetfeld verschwindet?
, so dass im Kreismittelpunkt das Magnetfeld verschwindet?
- Wie gross ist der Magnetfeldgradient in die Richtung des eingezeichneten Vektors
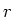 am
Kreismittelpunkt?
am
Kreismittelpunkt?
-
- Für
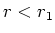 ist das magnetische Feld null, weil hier kein Strom fliesst.
Für einen Kreis mit dem Radius
ist das magnetische Feld null, weil hier kein Strom fliesst.
Für einen Kreis mit dem Radius
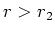 ist der resultierende Strom, der durch die Kontur fliesst, gleich null;
damit ist auch
ist der resultierende Strom, der durch die Kontur fliesst, gleich null;
damit ist auch  gleich null. Für
gleich null. Für 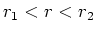 ergibt sich aus dem Ampère-Gesetz
ergibt sich aus dem Ampère-Gesetz
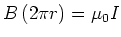 und damit
und damit
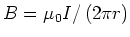 .
.
- Die magnetische Energiedichte ist
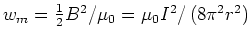 .
.
- Die gesamte magnetische Energie im Volumen zwischen den Zylindern ist
.
- Für die magnetische Energie können wir auch schreiben
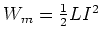 . Daraus folgt
. Daraus folgt
![$L/\ell=\left[ \mu_{0}/\left( 2\pi\right) \right] \ln r_{2}/r_{1}$](img46.gif) .
.
- Aufgrund der Definition der Gegeninduktivität
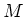 können wir für den zweiten Stromkreis schreiben
können wir für den zweiten Stromkreis schreiben
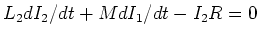 . Wir integrieren beide Seiten dieser Gleichung über die Zeit. Für den ersten
Term ergibt sich
. Wir integrieren beide Seiten dieser Gleichung über die Zeit. Für den ersten
Term ergibt sich
.
Entsprechend gilt für den zweiten Term
Schliesslich erhalten wir für den dritten Term
.
Daraus folgt
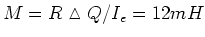 .
.
-
- Wir berechnen zunächst den durch den Stab fliessenden Strom. Die Spannungsquelle
liefert eine Spannung
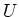 , und
der Stab induziert aufgrund seiner Bewegung eine Gegenspannung mit dem Betrag
, und
der Stab induziert aufgrund seiner Bewegung eine Gegenspannung mit dem Betrag 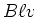 . Also ist die
resultierende Spannung
. Also ist die
resultierende Spannung 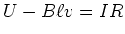 . Daraus folgt
. Daraus folgt
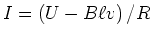 . Wegen dieses Stromes im Stab
wirkt auf ihn durch das magnetische Feld die Kraft
. Wegen dieses Stromes im Stab
wirkt auf ihn durch das magnetische Feld die Kraft
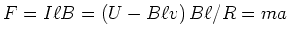 .
.
- Die Endgeschwindigkeit
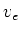 tritt auf, wenn
tritt auf, wenn  ist, also wenn gilt
ist, also wenn gilt
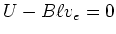 . Daraus folgt
. Daraus folgt
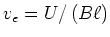 .
.
- Bei der Endgeschwindigkeit ist der Strom im Stab
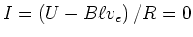 .
.
-
- Die unendlich langen geraden Abschnitte tragen zum Feld nichts bei, weil sie auf Geraden verlaufen, die durch
den Beobachtungspunkt gehen. Für den
kurzen Abschnitt gilt
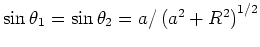 und damit
und damit
.
- Wir stellen uns den kurzen Abschnitt als eine Seite eines regelmässigen N-Ecks vor. Dann ist, vom Mittelpunkt
des Vielecks aus gesehen, der Winkel über jedem Abschnitt gleich
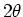 . Der gesamte Winkel im Vieleck ist
. Der gesamte Winkel im Vieleck ist
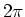 . Für ein
. Für ein 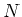 -Eck folgt daraus
-Eck folgt daraus
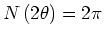 und
und 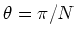 . Das Feld im Mittelpunkt des
N-Ecks ist dann
. Das Feld im Mittelpunkt des
N-Ecks ist dann
.
Der erste Faktor 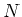 rührt daher, dass jede der N Seiten den gleichen Beitrag zum Feld liefert. Für sehr grosses N
ist der Winkel
rührt daher, dass jede der N Seiten den gleichen Beitrag zum Feld liefert. Für sehr grosses N
ist der Winkel 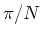 sehr klein; dann gilt
sehr klein; dann gilt
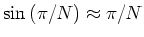 und damit
und damit
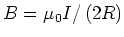 , genau wie im Mittelpunkt einer kreisförmigen Schleife.
, genau wie im Mittelpunkt einer kreisförmigen Schleife.
-
- Anfangs liegt keine Gegeninduktionsspannung vor, und der Strom ist
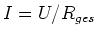 . Mit
. Mit 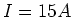 ist
ist
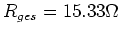 . Daher ist der Widerstand, der in Reihe zum Motor zu schalten ist,
. Daher ist der Widerstand, der in Reihe zum Motor zu schalten ist,
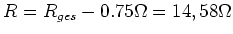 .
.
- Bei normaler Drehzahl ist der Spannungsabfall über dem Motor
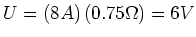 . Weil der Motor mit 230 V betrieben wird, entsteht eine Gegenspannung von 224 V.
. Weil der Motor mit 230 V betrieben wird, entsteht eine Gegenspannung von 224 V.
- Wenn sich der Fluss ändert, wird ein Strom induziert, für den gilt
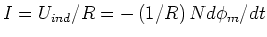 . Wegen
. Wegen 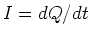 ist die Ladung, die die Spule passiert, gegeben durch
ist die Ladung, die die Spule passiert, gegeben durch
.
Dies gilt unabhängig davon, wie sich der Fluss von einem Wert zum anderen ändert.
-
- Das gesamte Feld in diesem System entsteht durch Überlagerung der Felder eines geraden Leiters und einer Schleife.
Das Feld des geraden Leiters hat den Betrag
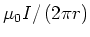 und weist aus der Papier-Ebene
heraus. Für den kreisförmigen Teil ist das Feld
und weist aus der Papier-Ebene
heraus. Für den kreisförmigen Teil ist das Feld
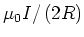 ;es weist in die Papier-Ebene hinein.
Hier ist
;es weist in die Papier-Ebene hinein.
Hier ist 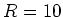 cm der Radius der Schleife. Damit die Felder einander aufheben, muss gelten
cm der Radius der Schleife. Damit die Felder einander aufheben, muss gelten
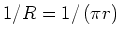 bzw.
bzw. 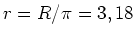 cm.
cm.
- Das Feld des Kreises mit dem Radius
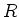 für einen Punkt ausserhalb des Zentrums ist
für einen Punkt ausserhalb des Zentrums ist
Wir parametrisieren den Kreis mit
und setzen das
neue Zentrum zu
Dann ist
und
Der vom Kreis herrührende Strom erzeugt das Magnetfeld
Das gesamte Magnetfeld ist dann
oder
mit
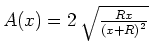 und mit
und mit
- Elliptisches Integral erster Art
-
- Elliptisches Integral zweiter Art
-
Wir leiten nach 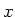 ab und erhalten
ab und erhalten
Übungsblatt 06
Grundkurs IIIb für Physiker
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html uebungsblatt06
The translation was initiated by marti on 2003-02-03


Up: Grundkurs IIIb für Physiker
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.3\textwidth]{ue-06-02.eps}](img4.gif)
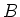 zu berechnen. Zeigen Sie, dass
zu berechnen. Zeigen Sie, dass 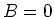 ist,
ausser zwischen den Leitern.
ist,
ausser zwischen den Leitern.
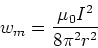
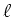 mit dem Volumen
mit dem Volumen
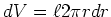 , und zeigen Sie durch Integration, dass
die gesamte magnetische Energie im Volumen der Länge
, und zeigen Sie durch Integration, dass
die gesamte magnetische Energie im Volumen der Länge 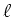
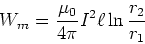
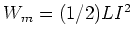 um zu zeigen,
dass die Selbstinduktivität pro Längeneinheit
um zu zeigen,
dass die Selbstinduktivität pro Längeneinheit
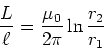
![\includegraphics[width=0.5\textwidth]{ue-06-01.eps}](img13.gif)
![\includegraphics[width=0.5\textwidth]{ue-06-05.eps}](img19.gif)
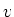 und formulieren Sie das
zweite Newtonsche Gesetz für den Stab, wenn er die Geschwindigkeit
und formulieren Sie das
zweite Newtonsche Gesetz für den Stab, wenn er die Geschwindigkeit 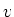 hat.
hat.
![\includegraphics[width=0.3\textwidth]{ue-06-03.eps}](img25.gif)
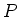 im Abstand
im Abstand 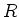 vom stromdurchflossenen Leiter.
vom stromdurchflossenen Leiter.
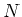 Seiten zu
berechnen.
Seiten zu
berechnen.
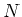 , die Lösung in diejenige für ein Magnetfeld in der Mitte
eines stromdurchflossenen Kreises übergeht.
, die Lösung in diejenige für ein Magnetfeld in der Mitte
eines stromdurchflossenen Kreises übergeht.
![\includegraphics[width=0.3\textwidth]{ue-06-04.eps}](img35.gif)
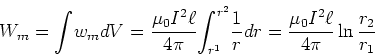
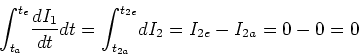
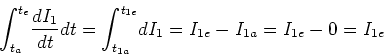
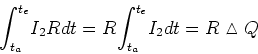
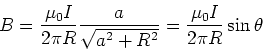
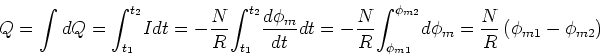
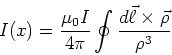
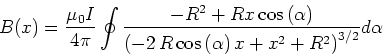
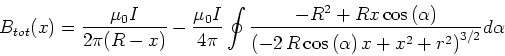
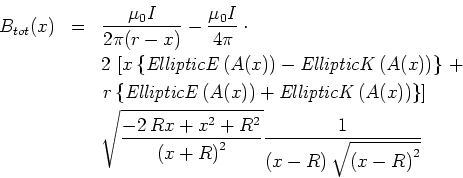
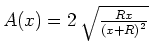 und mit
und mit