



Next: Hall-Effekt
Up: Elektrische Ströme
Previous: Die magnetische Kraft
Unterabschnitte
(Siehe Leisi, Klassische Physik II[Lei98, 98])
Versuch zur Vorlesung: Fadenstrahlrohr EM-11
Um nicht immer die Lorentz-Transformation ausrechnen zu müssen , führen wir die magnetische
Feldstärke oder die magnetische Induktion
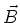 ein. Ein magnetisches Feld lenkt Elektronen ab. Wie wir schon früher gesehen haben, ist eine
Bewegung der Ladungsträger für die magnetische Kraft notwendig. Wird das Magnetfeld der
Helmholtzspulen so gedreht, dass es parallel zur Bewegungsrichtung der Elektronen liegt,
verschwindet die Magnetkraft. Das folgende Kraftgesetz
ein. Ein magnetisches Feld lenkt Elektronen ab. Wie wir schon früher gesehen haben, ist eine
Bewegung der Ladungsträger für die magnetische Kraft notwendig. Wird das Magnetfeld der
Helmholtzspulen so gedreht, dass es parallel zur Bewegungsrichtung der Elektronen liegt,
verschwindet die Magnetkraft. Das folgende Kraftgesetz
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{
\...
...quation}
\vec F_L = q \cdot \vec v \times \vec B
\end{equation}}\end{minipage}}](img718.gif)
beschreibt die magnetischen Kräfte auf Elektronen. Die Kraft 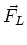 heisst Lorentz-Kraft.
heisst Lorentz-Kraft.
Durch den Vergleich von Gleichung (3.98) und Gleichung (3.96) kann man für die magnetische Feldstärke
einer linienförmigen Stromverteilung schreiben
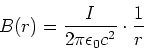 |
(3.96) |
Die Induktionskonstante
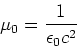 |
(3.97) |
ermöglicht es Gleichung (3.99) kompakter zu schreiben
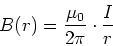 |
(3.98) |
|
Lage der magnetischen Induktion zum Strom und zur Geschwindigkeit der Ladung.
|
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{
D...
...tung, Finger zeigen in die Richtung der magnetischen Induktion).}\end{minipage}}](img724.gif)
Mathematisch kann man 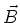 aus einem Linienelement
aus einem Linienelement 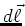 , das parallel zum Leiter und
damit zum Strom ist, und das in die Flussrichtung des Stromes zeigt und aus dem Vektor
, das parallel zum Leiter und
damit zum Strom ist, und das in die Flussrichtung des Stromes zeigt und aus dem Vektor 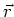 , der vom
Leiterelement zum Ort, an dem das Magnetfeld betrachtet werden sollte, zeigt, berechnen
, der vom
Leiterelement zum Ort, an dem das Magnetfeld betrachtet werden sollte, zeigt, berechnen
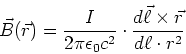 |
(3.99) |
Versuch zur Vorlesung: Magnetische Feldlinien EM-50
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Di...
...r Mittelpunkt der kreisf{\uml o}rmigen Feldlinien ist der
Strom.}\end{minipage}}](img727.gif)
Die Kraft zwischen zwei stromdurchflossenen Leitern kann neu berechnet werden. Mit
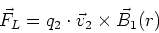 |
(3.100) |
wobei 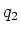 eine Ladung im Leiter 2 ist, und mit
eine Ladung im Leiter 2 ist, und mit 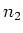 der Ladungsträgerdichte im Leiter 2,
der Ladungsträgerdichte im Leiter 2, 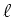 die
betrachtete Länge,
die
betrachtete Länge, 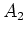 der Querschnitt des Leiters und
der Querschnitt des Leiters und
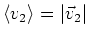 , bekommt man
, bekommt man
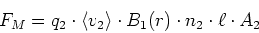 |
(3.101) |
Der Strom im Leiter 2 ist nun aber
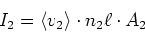 |
(3.102) |
Damit ist
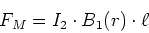 |
(3.103) |
Wenn wir Gleichung (3.101) einsetzen, bekommen wir
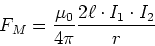 |
(3.104) |
Diese Gleichung wird zur Definition der Einheit der magnetischen Induktion im SI-System verwendet.
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{
\...
...ation}
\frac{\mu_0}{4\pi} = 10^{-7}\frac{N}{A^2}
\end{equation}}\end{minipage}}](img737.gif)
Materialien
Übungsblatt 05 vom 12. 12. 2002
(HTML
oder
PDF)
Folien zur Vorlesung am 12. 12. 2002 (PDF)
Die Einheit der magnetischen Induktion ist
![\begin{displaymath}[B]= Tesla = T = \frac{N\cdot s}{C \cdot m} = \frac{N}{A m}= \frac{V\cdot s}{m^2}
\end{displaymath}](img739.gif) |
(3.105) |
- Die gesamte Kraft einer bewegten Ladung
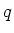 in einer beliebigen Ladungs- und Stromverteilung ist
in einer beliebigen Ladungs- und Stromverteilung ist
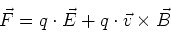 |
(3.106) |
Dies ist das Kraftgesetz der Elektrodynamik
- Das magnetische Feld ist kein fundamentales Feld, sondern eine relativistische Korrektur zu dem
elektrostatischen Feld.
Die Kraft auf einen stromdurchflossenen Leiter in einem beliebigen Magnetfeld kann mit dem Gesetz von
Biot-Savart berechnet werden.
|
Berechnung der Kraft auf ein Leiterelement.
|
Der Betrag des Vektors 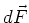 , der senkrecht auf
, der senkrecht auf
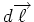 und senkrecht auf
und senkrecht auf 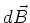 steht, ist
steht, ist
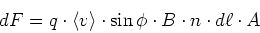 |
(3.107) |
wobei 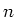 die Dichte der Ladungsträger und
die Dichte der Ladungsträger und 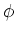 der Winkel zwischen
der Winkel zwischen 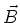 und
und
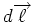 ist. Mit der Stromdichte
ist. Mit der Stromdichte
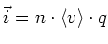 erhalten wir
erhalten wir
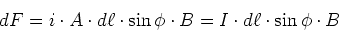 |
(3.108) |
Die vektorielle Schreibweise der Biot-Savart-Kraft ist
demnach
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{
\...
...ation}
d\vec F = I\cdot d\vec \ell \times \vec B
\end{equation}}\end{minipage}}](img750.gif)
Beispiele
- Die Kraft für eine beliebig geformte geschlossene Leiterschleife in einem homogenen Magnetfeld ist
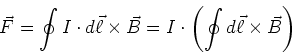 |
(3.109) |
Da das Linienintegral
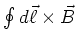 über eine geschlossene Schleife null ist (die positiven und die negativen Anteile heben
sich auf) ist
über eine geschlossene Schleife null ist (die positiven und die negativen Anteile heben
sich auf) ist 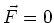 .
.
- Das Drehmoment auf eine Leiterschlaufe in einem homogenen Magnetfeld kann durch summieren der
Kraftanteile auf die vier Segmente berechnet werden.
Versuch zur Vorlesung: Elektromotor Applet
Versuch zur Vorlesung: Lorentz-Kraft EM046
|
Drehmoment auf eine Leiterschleife im homogenen Magnetfeld
|
Bezüglich 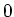 ist die Situation symmetrisch. Die in der Zeichnung vertikalen Leiterelemente liefern
kollineare sich aufhebende Kräfte. Die horizontalen Segmente ergeben das Drehmoment
ist die Situation symmetrisch. Die in der Zeichnung vertikalen Leiterelemente liefern
kollineare sich aufhebende Kräfte. Die horizontalen Segmente ergeben das Drehmoment
Das gesamte Drehmoment ist
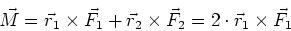 |
(3.111) |
Das Drehmoment 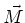 liegt in der Ebene der Leiterschlaufe. Wenn
liegt in der Ebene der Leiterschlaufe. Wenn 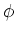 der Winkel zwischen der
Normalen auf die Ebene der Leiterschlaufe und
der Winkel zwischen der
Normalen auf die Ebene der Leiterschlaufe und 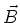 ist, gilt mit
ist, gilt mit
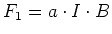 :
:
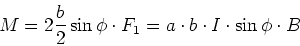 |
(3.112) |
Wir definieren das magnetische Moment 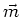 so, dass es senkrecht auf die Ebene der Leiterschlaufe steht und dass
so, dass es senkrecht auf die Ebene der Leiterschlaufe steht und dass
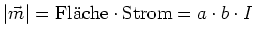 ist. Damit ist
ist. Damit ist
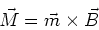 |
(3.113) |
Das Drehmoment auf eine Leiterschlaufe im homogenen Magnetfeld wird in
Drehspulinstrumenten, in Motoren oder bei der
Sichtbarmachung von Magnetfeldern mit Eisenfeilspänen verwendet.
- Die potentielle Energie einer um den Winkel
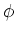 gegenüber dem Magnetfeld verdrehten
stromdurchflossenen Leiterschlaufe wird berechnet, indem man von
gegenüber dem Magnetfeld verdrehten
stromdurchflossenen Leiterschlaufe wird berechnet, indem man von 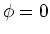 ausgeht und die Schlaufe
langsam zum Winkel
ausgeht und die Schlaufe
langsam zum Winkel 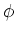 dreht. Die Arbeit, um von
dreht. Die Arbeit, um von 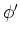 nach
nach 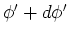 zu drehen ist
zu drehen ist
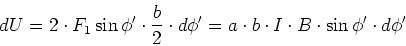 |
(3.114) |
Damit erhalten wir
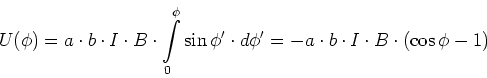 |
(3.115) |
Wenn wir
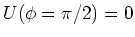 wählen haben wir
wählen haben wir
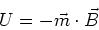 |
(3.116) |
Ein weiteres Beispiel einer Kraftwirkung auf Ladungen ist das Barlowsche Rad.
Versuch zur Vorlesung: Barlowsches Rad EM004
(Siehe Leisi, Klassische Physik II[Lei98, 104])
Beim unendlich ausgedehnten geraden Leiter war das durch einen Strom 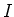 erzeugte Magnetfeld durch
kreisförmige Magnetfeldlinien mit der Stärke
erzeugte Magnetfeld durch
kreisförmige Magnetfeldlinien mit der Stärke
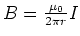 charakterisiert, wobei das
charakterisiert, wobei das 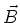 -Feld tangential zu den Kreisen liegt. Das Linienintegral entlang der Feldlinien, also entlang des Kreises
-Feld tangential zu den Kreisen liegt. Das Linienintegral entlang der Feldlinien, also entlang des Kreises
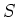 , ergibt
, ergibt
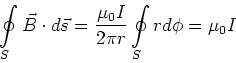 |
(3.117) |
Dieses Linienintegral ist unabhängig von 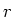 . Die Behauptung ist, das die obige Gleichung, ein einfacher Fall
des Ampèreschen Durchflutungsgesetzes, allgemeingültig ist.
. Die Behauptung ist, das die obige Gleichung, ein einfacher Fall
des Ampèreschen Durchflutungsgesetzes, allgemeingültig ist.
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Am...
...imits_{A(S)}\!\!\!\!\!\!\int \vec i \cdot d\vec a
\end{equation}}\end{minipage}}](img775.gif)
Der Beweis geht in mehreren Schritten:
- Eine beliebige Kurve
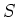 um einen geraden Leiter
um einen geraden Leiter
-
![\includegraphics[width=0.5\textwidth]{strom-009.eps}](img776.gif)
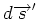 ist die Projektion des Weglängenelementes
ist die Projektion des Weglängenelementes
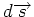 auf der Kurve
auf der Kurve 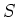 auf die in der
auf die in der
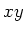 -Ebene liegende Projektion der Kurve
-Ebene liegende Projektion der Kurve 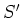 . Es ist
. Es ist
da 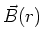 keine Komponente in die
keine Komponente in die 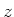 -Richtung hat. Es ist
-Richtung hat. Es ist
und damit
- Eine beliebige Kurve
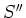 , die den Leiter nicht umschliesst
, die den Leiter nicht umschliesst
- Es ist
Das bedeutet, dass Ströme durch Leiter, die nicht vom Integrationsweg 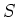 umschlossen werden, keinen
Beitrag zum Integral geben.
umschlossen werden, keinen
Beitrag zum Integral geben.
- Eine beliebige Kurve
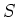 um eine beliebige Stromverteilung
um eine beliebige Stromverteilung
- Wir betrachten viele Ströme
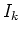 , die
von der Integrationskurve
, die
von der Integrationskurve 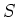 umschlossen werden. Wegen der Linearität des Problems gilt
umschlossen werden. Wegen der Linearität des Problems gilt
wobei diejenigen Ströme, die mit dem Umlaufsinn von 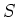 eine Rechtsschraube bilden, positiv zu zählen sind.
eine Rechtsschraube bilden, positiv zu zählen sind.
Beispiel
Ein zylindrischer Leiter mit dem Radius 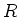 soll homogen vom Strom
soll homogen vom Strom 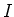 durchflossen werden. Aus
Symmetriegründen sind die Magnetfeldlinien konzentrische Kreise um den Leiter. Ausserhalb des Leiters (
durchflossen werden. Aus
Symmetriegründen sind die Magnetfeldlinien konzentrische Kreise um den Leiter. Ausserhalb des Leiters (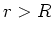 )
haben wir
)
haben wir
Innerhalb des Leiters (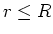 ) gilt
) gilt
Mit dem Stokeschen Satz (Gleichung (A.3) ) kann man die Integralform des Ampèreschen Gesetzes umschreiben
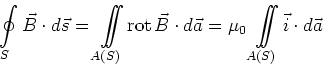 |
(3.118) |
Da diese Gleichungen für alle Integrationsflächen 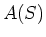 gelten müssen, muss auch die differentielle Form des
Ampèreschen Gesetzes gelten
gelten müssen, muss auch die differentielle Form des
Ampèreschen Gesetzes gelten
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{
\...
...{equation}
\textrm{rot} {}\vec B = \mu_0 \vec i
\end{equation}}\end{minipage}}](img794.gif)
Beispiel: homogene Stromverteilung in einem unendlich ausgedehnten Leiter
|
Magnetfeld einer homogenen Stromverteilung in einer dünnen Platte. Links: die Geometrie zur
Berechnung, Mitte: das Magnetfeld eines homogenen Stromflusses und Rechts: das Magnetfeld zweier antiparallel
von Strom durchflossener Platten.
|
Wir definieren eine lineare Stromdichte
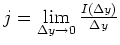 . Das Stromfeld können wir uns als Parallelschaltung vieler linearer Leiter vorstellen. Aus dem
Superpositionsprinzip folgt, dass
. Das Stromfeld können wir uns als Parallelschaltung vieler linearer Leiter vorstellen. Aus dem
Superpositionsprinzip folgt, dass
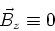 |
(3.119) |
Das resultierende Feld dieser Superposition muss in der 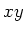 -Ebene liegen. Auf den beiden Seiten senkrecht
zur Platte finden sich immer zwei Stromfäden, die die
-Ebene liegen. Auf den beiden Seiten senkrecht
zur Platte finden sich immer zwei Stromfäden, die die 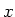 -Komponente kompensieren. Wenn wir später das
Ampèresche Gesetz auf diese beiden Seiten anwenden, gibt es keine Komponente von
-Komponente kompensieren. Wenn wir später das
Ampèresche Gesetz auf diese beiden Seiten anwenden, gibt es keine Komponente von 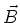 parallel zur Seite:
dieser Teil des Linienintegrals ist null.
parallel zur Seite:
dieser Teil des Linienintegrals ist null.
Wir betrachten weiter das Feld 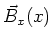 und
und 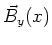 im Abstand
im Abstand 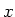 von der Platte. Wir werden zwei
Symmetrieoperationen an:
von der Platte. Wir werden zwei
Symmetrieoperationen an:
- Wir drehen die Platte um
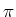 um die
um die 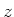 -Achse. Die neue Situation (Ströme) ist identisch mit der
Ursprungssituation. Deshalb muss
-Achse. Die neue Situation (Ströme) ist identisch mit der
Ursprungssituation. Deshalb muss
sein.
- Wir drehen die Platte um
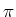 um die
um die 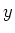 -Achse und drehen gleichzeitig die Flussrichtung des
Stromes um
-Achse und drehen gleichzeitig die Flussrichtung des
Stromes um
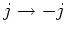 . Die Endsituation ist ununterscheidbar von der am Anfang. Also gilt auch
. Die Endsituation ist ununterscheidbar von der am Anfang. Also gilt auch
und
.
Mit den beiden Symmetrieüberlegungen folgt:
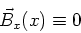 |
(3.120) |
Um 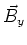 zu bestimmen, nehmen wir an, dass unser Integrationspfad
zu bestimmen, nehmen wir an, dass unser Integrationspfad 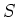 symmetrisch bezüglich der Platte
ist. Das Ampèresche Gesetz sagt
symmetrisch bezüglich der Platte
ist. Das Ampèresche Gesetz sagt
Das Resultat ist unabhängig von 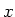 und homogen im Raum. Die Magnetfeldlinien sind
parallel zur Platte und links und rechts antiparallel (siehe Abbildung oben Mitte).
und homogen im Raum. Die Magnetfeldlinien sind
parallel zur Platte und links und rechts antiparallel (siehe Abbildung oben Mitte).
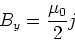 |
(3.121) |
Bei zwei antiparallel von Strom durchflossenen Platten ist das Magnetfeld auf den Raum zwischen den Platten
beschränkt.
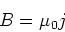 |
(3.122) |
Anwendungsbeispiele: Streifenleiter, Koaxialkabel
(Siehe Leisi, Klassische Physik II[Lei98, 111])
In diesem Abschnitt soll gezeigt werden, dass das Magnetfeld quellenfrei
ist.
|
Integrationsfläche zur Analyse der Quellenfreiheit des Magnetfeldes
|
Da überall auf der Integrationsfläche 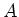 gilt:
gilt:
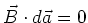 , ist
, ist
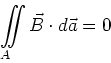 |
(3.123) |
Materialien
Folien zur Vorlesung am 19. 12. 2002 (PDF)
Wir verallgemeinern das Resultat, indem wir einen Zylinder mit beliebiger Grund- und Deckfläche nehmen. Auf
der Grund und Deckfläche gilt das vorherige Argument, so dass
ist.
|
Integration über die Mantelfläche.
|
An der Mantelfläche gilt mit
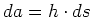
und damit
Damit gilt auch für allgemeine Zylinderflächen
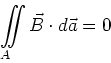 |
(3.124) |
Mit diesem Resultat zeigt man, dass dieses Integral für beliebige Flächen um einen Leiter null ist.
Schliesslich zeigt man, dass das Resultat auch für beliebige Stromverteilungen gilt. Mit dem Gaussschen Satz
(Gleichung (A.1) ) zeigt man
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Qu...
...orm
\begin{equation}
\textrm{div} {}\vec B = 0
\end{equation} }\end{minipage}}](img820.gif)
Die Quellenfreiheit des magnetischen Feldes bedeutet, dass es keine magnetischen
Ladungen gibt und dass die Feldlinien im Endlichen geschlossen sind.
(Siehe Leisi, Klassische Physik II[Lei98, 114])
Versuch zur Vorlesung: Magnetfeld von Leitern Em021
Jedes Magnetfeld muss das Ampèresche Gesetz
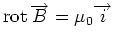 und die Quellenfreiheit
und die Quellenfreiheit
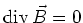 erfüllen. Analog zur Poissongleichung Gleichung (2.69) soll
auch für das Magnetfeld eine Potentialgleichung gelten. Mit dem Vektorpotential
erfüllen. Analog zur Poissongleichung Gleichung (2.69) soll
auch für das Magnetfeld eine Potentialgleichung gelten. Mit dem Vektorpotential
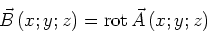 |
(3.125) |
werden beide Gleichungen erfüllt. Wegen der Vektoridentität
 |
(3.126) |
ist die Quellenfreiheit bei beliebiger Wahl von 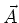 garantiert. Mit der zweiten Vektoridentität
garantiert. Mit der zweiten Vektoridentität
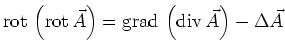 bekommen wir aus
dem Ampèrschen Gesetz
bekommen wir aus
dem Ampèrschen Gesetz
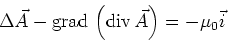 |
(3.127) |
Das Vektorpotential 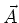 kann immer so gewählt werden, dass
kann immer so gewählt werden, dass
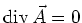 gilt. Das Vektorpotential
ist nicht eindeutig bestimmt. Nehmen wir an, dass ein Vektorpotential mit
gilt. Das Vektorpotential
ist nicht eindeutig bestimmt. Nehmen wir an, dass ein Vektorpotential mit
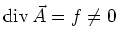 existiert. Dann existiert auch ein Vektorfeld
existiert. Dann existiert auch ein Vektorfeld 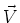 mit
mit
mit einer eindeutigen Lösung, denn die obigen Gleichungen sind formal äquivalent zur Elektrostatik.
Wir definieren Ein Vektorpotential
Wegen Gleichung (3.138) gilt dann
Dies bedeutet, dass das neue Vektorpotential das gleiche 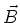 -Feld erzeugt wie das ursprüngliche. Wegen
Gleichung (3.138) gilt auch
-Feld erzeugt wie das ursprüngliche. Wegen
Gleichung (3.138) gilt auch
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Zu...
...A'$ gefunden werden, so dass
$\textrm{div} {}\vec A = 0$ ist.}\end{minipage}}](img837.gif)
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Da...
...ml o}renden Potentiale nennt man
\textbf{Eichung}\index{Eichung}}\end{minipage}}](img838.gif)
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{In...
...{Quantenmechanik} rechnet man bevorzugt mit dem
Vektorpotential.}\end{minipage}}](img839.gif)
Aus der Gleichung für das Vektorpotential einer Stromverteilung
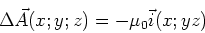 |
(3.129) |
kann man die Umkehrfunktion berechnen und erhält, analog zur Elektrostatik,
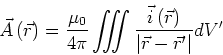 |
(3.130) |
Wenn wir mit
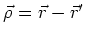 den Abstand von einem Beobachtungspunkt
den Abstand von einem Beobachtungspunkt 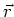 zu
einem Punkt
zu
einem Punkt 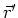 mit der Stromdichte
mit der Stromdichte
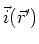 eines linearen Leiterstückes
eines linearen Leiterstückes
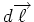 bezeichnen und
bezeichnen und
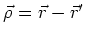 setzen, ist der Beitrag zum magnetischen Feld
setzen, ist der Beitrag zum magnetischen Feld
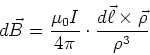 |
(3.131) |
Durch Integration der Formel von Laplace oder des Gesetzes von
Biot-Savart bekommt man
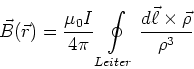 |
(3.132) |
Mit diesem Gesetz kann man das Magnetfeld einer beliebigen Spule berechnen. Achtung: nur die
integrale Form hat eine physikalische Bedeutung! Die Formel von Laplace wird über das Vektorpotential
berechnet.

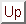



Next: Hall-Effekt
Up: Elektrische Ströme
Previous: Die magnetische Kraft
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() ein. Ein magnetisches Feld lenkt Elektronen ab. Wie wir schon früher gesehen haben, ist eine
Bewegung der Ladungsträger für die magnetische Kraft notwendig. Wird das Magnetfeld der
Helmholtzspulen so gedreht, dass es parallel zur Bewegungsrichtung der Elektronen liegt,
verschwindet die Magnetkraft. Das folgende Kraftgesetz
ein. Ein magnetisches Feld lenkt Elektronen ab. Wie wir schon früher gesehen haben, ist eine
Bewegung der Ladungsträger für die magnetische Kraft notwendig. Wird das Magnetfeld der
Helmholtzspulen so gedreht, dass es parallel zur Bewegungsrichtung der Elektronen liegt,
verschwindet die Magnetkraft. Das folgende Kraftgesetz
![]() heisst Lorentz-Kraft.
heisst Lorentz-Kraft.
![\includegraphics[width=0.7\textwidth]{strom-006.eps}](img723.gif)
![]() aus einem Linienelement
aus einem Linienelement ![]() , das parallel zum Leiter und
damit zum Strom ist, und das in die Flussrichtung des Stromes zeigt und aus dem Vektor
, das parallel zum Leiter und
damit zum Strom ist, und das in die Flussrichtung des Stromes zeigt und aus dem Vektor ![]() , der vom
Leiterelement zum Ort, an dem das Magnetfeld betrachtet werden sollte, zeigt, berechnen
, der vom
Leiterelement zum Ort, an dem das Magnetfeld betrachtet werden sollte, zeigt, berechnen
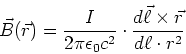
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Di...
...r Mittelpunkt der kreisf{\uml o}rmigen Feldlinien ist der
Strom.}\end{minipage}}](img727.gif)
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{
\...
...ation}
\frac{\mu_0}{4\pi} = 10^{-7}\frac{N}{A^2}
\end{equation}}\end{minipage}}](img737.gif)
![\includegraphics[width=0.7\textwidth]{strom-007.eps}](img741.gif)
![]() , der senkrecht auf
, der senkrecht auf
![]() und senkrecht auf
und senkrecht auf ![]() steht, ist
steht, ist
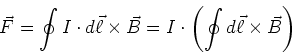
![\includegraphics[width=0.7\textwidth]{strom-008.eps}](img754.gif)
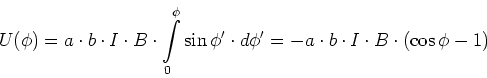
![]() erzeugte Magnetfeld durch
kreisförmige Magnetfeldlinien mit der Stärke
erzeugte Magnetfeld durch
kreisförmige Magnetfeldlinien mit der Stärke
![]() charakterisiert, wobei das
charakterisiert, wobei das ![]() -Feld tangential zu den Kreisen liegt. Das Linienintegral entlang der Feldlinien, also entlang des Kreises
-Feld tangential zu den Kreisen liegt. Das Linienintegral entlang der Feldlinien, also entlang des Kreises
![]() , ergibt
, ergibt
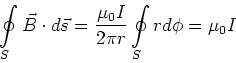
![\includegraphics[width=0.5\textwidth]{strom-009.eps}](img776.gif)
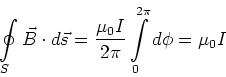
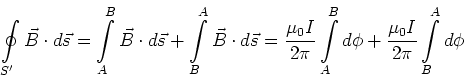
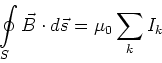
![]() soll homogen vom Strom
soll homogen vom Strom ![]() durchflossen werden. Aus
Symmetriegründen sind die Magnetfeldlinien konzentrische Kreise um den Leiter. Ausserhalb des Leiters (
durchflossen werden. Aus
Symmetriegründen sind die Magnetfeldlinien konzentrische Kreise um den Leiter. Ausserhalb des Leiters (![]() )
haben wir
)
haben wir
![]() ) gilt
) gilt
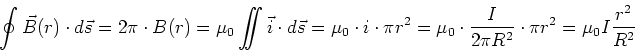
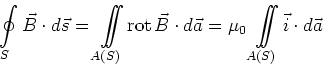
![\includegraphics[width=0.9\textwidth]{strom-014.eps}](img795.gif)
![]() . Das Stromfeld können wir uns als Parallelschaltung vieler linearer Leiter vorstellen. Aus dem
Superpositionsprinzip folgt, dass
. Das Stromfeld können wir uns als Parallelschaltung vieler linearer Leiter vorstellen. Aus dem
Superpositionsprinzip folgt, dass
![]() und
und ![]() im Abstand
im Abstand ![]() von der Platte. Wir werden zwei
Symmetrieoperationen an:
von der Platte. Wir werden zwei
Symmetrieoperationen an:
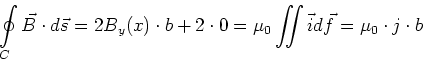
![\includegraphics[width=0.4\textwidth]{strom-010.eps}](img810.gif)
![]() gilt:
gilt:
![]() , ist
, ist
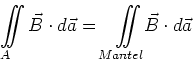
![\includegraphics[width=0.5\textwidth]{strom-011.eps}](img815.gif)
![]()
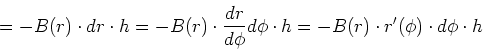
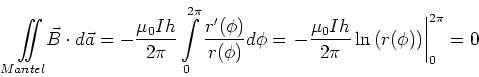
![]() und die Quellenfreiheit
und die Quellenfreiheit
![]() erfüllen. Analog zur Poissongleichung Gleichung (2.69) soll
auch für das Magnetfeld eine Potentialgleichung gelten. Mit dem Vektorpotential
erfüllen. Analog zur Poissongleichung Gleichung (2.69) soll
auch für das Magnetfeld eine Potentialgleichung gelten. Mit dem Vektorpotential
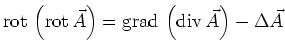 bekommen wir aus
dem Ampèrschen Gesetz
bekommen wir aus
dem Ampèrschen Gesetz
![]() kann immer so gewählt werden, dass
kann immer so gewählt werden, dass
![]() gilt. Das Vektorpotential
ist nicht eindeutig bestimmt. Nehmen wir an, dass ein Vektorpotential mit
gilt. Das Vektorpotential
ist nicht eindeutig bestimmt. Nehmen wir an, dass ein Vektorpotential mit
![]() existiert. Dann existiert auch ein Vektorfeld
existiert. Dann existiert auch ein Vektorfeld ![]() mit
mit
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Zu...
...A'$ gefunden werden, so dass
$\textrm{div} {}\vec A = 0$ ist.}\end{minipage}}](img837.gif)
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Da...
...ml o}renden Potentiale nennt man
\textbf{Eichung}\index{Eichung}}\end{minipage}}](img838.gif)
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{In...
...{Quantenmechanik} rechnet man bevorzugt mit dem
Vektorpotential.}\end{minipage}}](img839.gif)
![]() den Abstand von einem Beobachtungspunkt
den Abstand von einem Beobachtungspunkt ![]() zu
einem Punkt
zu
einem Punkt ![]() mit der Stromdichte
mit der Stromdichte
![]() eines linearen Leiterstückes
eines linearen Leiterstückes
![]() bezeichnen und
bezeichnen und
![]() setzen, ist der Beitrag zum magnetischen Feld
setzen, ist der Beitrag zum magnetischen Feld