
In diesem Abschnitt wollen wir aus einer mikroskopische Betrachtung einen Zusammenhang zwischen der relativen
Dielektrizitätszahl und der Polarisierbarkeit ableiten. Die Polarisation eines Atoms
oder Moleküls hängt von der Polarisierbarkeit ![]() sowie vom lokalen elektrischen Feld
sowie vom lokalen elektrischen Feld
![]() ab. Dieses lokale Feld ist die Summe aus dem externen Feld
ab. Dieses lokale Feld ist die Summe aus dem externen Feld ![]() sowie dem Feld aller
anderen Dipole am Beobachtungsort,
sowie dem Feld aller
anderen Dipole am Beobachtungsort, ![]() .
.
| (2.114) |
Die Polarisation hängt vom lokalen Feld
![]() wie folgt ab:
wie folgt ab:
wobei ![]() die Dichte der induzierten Dipole ist.
die Dichte der induzierten Dipole ist.
![\includegraphics[width=0.7\textwidth]{elektrostatik-033}](img583.gif)
|
Zur Berechnung von ![]() und damit
und damit
![]() betrachten wir ein homogenes Dielektrikum mit
betrachten wir ein homogenes Dielektrikum mit
![]() , bei dem ein kugelförmiges kleines Volumen mit dem Radius
, bei dem ein kugelförmiges kleines Volumen mit dem Radius ![]() entfernt wurde.
In diesem Volumen berechnen wir das lokale Feld[Som78, 68],das von einem externen Feld
entfernt wurde.
In diesem Volumen berechnen wir das lokale Feld[Som78, 68],das von einem externen Feld ![]() in der
in der ![]() -Richtung hervorgerufen wird. Das Dielektrikum erzeugt an der
Oberfläche des Hohlraums eine Ladungsdichte
-Richtung hervorgerufen wird. Das Dielektrikum erzeugt an der
Oberfläche des Hohlraums eine Ladungsdichte
![]() , analog wie eine Ladungsdichte
und ein elektrisches Feld mit
, analog wie eine Ladungsdichte
und ein elektrisches Feld mit
![]() zusammenhängt. Nach dem Coulombgesetz (Gleichung (2.5) ) ist
der Beitrag von
zusammenhängt. Nach dem Coulombgesetz (Gleichung (2.5) ) ist
der Beitrag von ![]() gegeben durch
gegeben durch
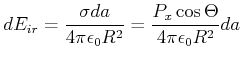 |
(2.116) |
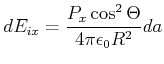 |
(2.117) |
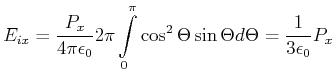 |
(2.118) |
| (2.120) |
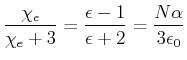 |
(2.121) |
Die Rechnung verläuft folgendermassen
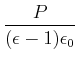 |
|||
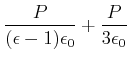 |
|||
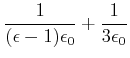 |
|||
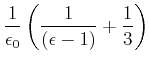 |
|||
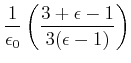 |
|||
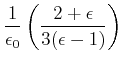 |
|||
