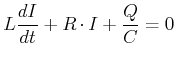




Next: Elektromotoren
Up: Das Faradaysche Induktionsgesetz
Previous: Kirchhoffsche Gesetze
Contents
Index
| Dieser Stoff wurde am 3. 2. 2005
behandelt |
![\includegraphics[height=8mm]{icon-mat}](img217.gif) |
Materialien
Folien zur Vorlesung vom 03. 02. 2005: PDFSeminar vom 03. 02. 2004: Aufgabenblatt 07
(HTML
oder
PDF)
|
In diesem Abschnitt betrachten wir die Wirkung von cosinusförmigen Wechselspannungen
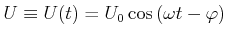 |
(4.338) |
Die Zeitskala für die Wechselspannung wird so gewählt, dass 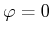 ist. Weiter setzen wir voraus, dass die
zeitliche Änderung aller Grössen so gering sind, dass wir wie im stationären Falle rechnen können. Wir dies den
quasistationären Fall.
ist. Weiter setzen wir voraus, dass die
zeitliche Änderung aller Grössen so gering sind, dass wir wie im stationären Falle rechnen können. Wir dies den
quasistationären Fall.
|
Definition von Strömen und Spannungen bei Wechselspannungen
|
Da bei Wechselspannungen a priori keine Stromrichtung vorgegeben ist, definiert man, zum Beispiel wie in der
Abbildung oben, die Stromrichtung zu einem bestimmten Zeitpunkt, hier für 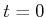 . Zu jedem Zeitpunkt muss die
Spannung im Stromkreis insgesamt null sein. Also ist
. Zu jedem Zeitpunkt muss die
Spannung im Stromkreis insgesamt null sein. Also ist
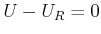 |
(4.339) |
und mit dem Ohmschen Gesetz
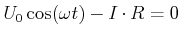 |
(4.340) |
oder
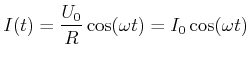 |
(4.341) |
Der Strom und die Spannung erreichen immer dann einen Extremwert, wenn 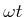 ein ganzzahliges Vielfaches von
ein ganzzahliges Vielfaches von
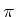 ist. Der durch einen Widerstand fliessende Strom ist in Phase mit der Spannung.
ist. Der durch einen Widerstand fliessende Strom ist in Phase mit der Spannung.
Die momentane Leistung am Widerstand ist
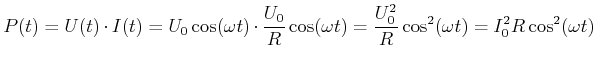 |
(4.342) |
Der Mittelwert der Leistung ist (
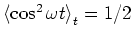 )
)
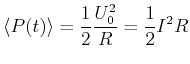 |
(4.343) |
Unter dem Effektivwert der Spannung (des Stromes) versteht man diejenige Gleichspannung, die an einem Ohmschen
Widerstand die gleiche Verlustleistung erzeugt. Also ist für sinusförmige Spannungen
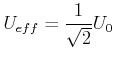 |
(4.344) |
beziehungsweise
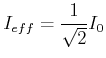 |
(4.345) |
Für beliebige Spannungsverläufe (Stromverläufe) ist der Effektivwert (auch rms-Wert von ''Root Mean Square'')
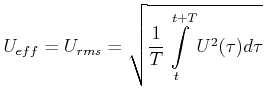 |
(4.346) |
wobei 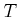 eine Zeit ist, die bei periodischen Signalen der Periodendauer entspricht und bei zufälligen Signalen
lang gegenüber der charakteristischen Zeitdauer der Schwankungen sein muss. Für Ströme gilt die analoge Formel
eine Zeit ist, die bei periodischen Signalen der Periodendauer entspricht und bei zufälligen Signalen
lang gegenüber der charakteristischen Zeitdauer der Schwankungen sein muss. Für Ströme gilt die analoge Formel
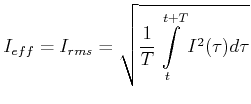 |
(4.347) |
|
Spule mit Wechselspannung
|
Wir verwenden Gleichung (4.25) um die Spannung über der Spule zu berechnen. Die induzierte Spannung ist der
Flussänderung entgegengesetzt. Sie wirkt so, dass die Zunahme des Stromes bei zunehmender Anregungsspannung
gebremst wird. Deshalb ist
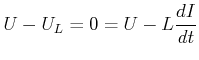 |
(4.348) |
Setzen wir
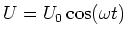 ein, erhalten wir
ein, erhalten wir
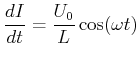 |
(4.349) |
und damit
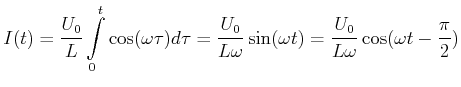 |
(4.350) |
Der Strom hat also den Scheitelwert
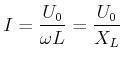 |
(4.351) |
wobei
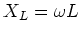 die Impedanz oder der induktive Widerstand der Spule ist. Die Einheit der Impedanz ist
gleich wie die Einheit des Widerstandes, das Ohm. Der Strom folgt der Spannung mit einer Phasenverschiebung von
die Impedanz oder der induktive Widerstand der Spule ist. Die Einheit der Impedanz ist
gleich wie die Einheit des Widerstandes, das Ohm. Der Strom folgt der Spannung mit einer Phasenverschiebung von
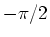 . Für die Effektivwerte gilt
. Für die Effektivwerte gilt
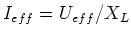 , da für sinusförmige Spannungen und Ströme der gleiche
Faktor zur Umrechnung von Scheitelwerten zu Effektivwerten verwendet werden muss.
, da für sinusförmige Spannungen und Ströme der gleiche
Faktor zur Umrechnung von Scheitelwerten zu Effektivwerten verwendet werden muss.
Die momentan dissipierte Leistung an einer Spule ist
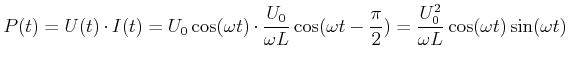 |
(4.352) |
Die dissipierte Leistung kann sowohl positiv wie auch negativ sein. Die mittlere dissipierte Leistung ist
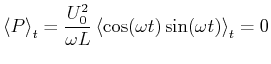 |
(4.353) |
Im Mittel wird also keine Leistung an einer Spule dissipiert.
|
Kondensator mit Wechselspannung
|
Beim Kondensator ist 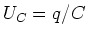 . Diese Spannung muss gleich der treibenden Spannung sein.
. Diese Spannung muss gleich der treibenden Spannung sein.
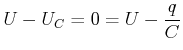 |
(4.354) |
Wir setzen 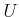 ein und erhalten
ein und erhalten
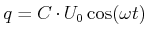 |
(4.355) |
Der Strom ist dann für den Strom
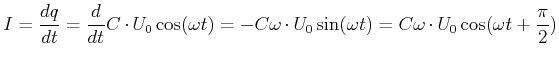 |
(4.356) |
Wir nennen
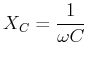 |
(4.357) |
die Impedanz des Kondensators. Der Scheitelwert des Stromes ist
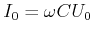 |
(4.358) |
Analog wie bei der Spule gilt die Gleichung
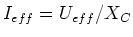 mit der gleichen Begründung auch für
Kondensatoren. Die momentan dissipierte Leistung ist
mit der gleichen Begründung auch für
Kondensatoren. Die momentan dissipierte Leistung ist
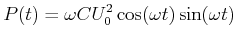 |
(4.359) |
Sie ist, analog wie bei der Spule, positiv oder negativ. Deshalb ist die mittlere dissipierte Leistung
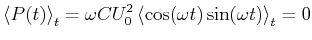 |
(4.360) |
Der Kondensator soll zur Zeit 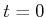 auf die Spannung
auf die Spannung 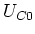 aufgeladen sein. Zur Zeit
aufgeladen sein. Zur Zeit 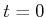 wird der Schalter
geschlossen. Die Differentialgleichung dieser Schaltung lautet:
wird der Schalter
geschlossen. Die Differentialgleichung dieser Schaltung lautet:
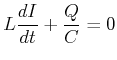 |
(4.361) |
Wir differenzieren einmal und bekommen
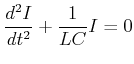 |
(4.362) |
Dies ist die aus der Mechanik bekannte Schwingungsdifferentialgleichung. Durch Analogieschluss sieht man, dass die
Resonanzfrequenz
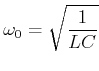 |
(4.363) |
ist.
|
Schwingkreis mit Widerstand
|
Der gedämpfte Schwingkreis enthält neben dem Kondensator und der Spule auch einen Widerstand. Die
Differentialgleichung des gedämpften Schwingkreises ist
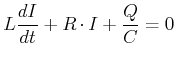 |
(4.364) |
Wir differenzieren einmal und bekommen
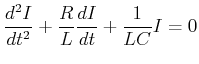 |
(4.365) |
Analog zur Mechanik ist die
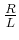 der Dämpfungsterm. Das in der Mechanik berechnete Verhalten eines
schwingungsfähigen Systems gilt auch für den elektrischen Schwingkreis.
der Dämpfungsterm. Das in der Mechanik berechnete Verhalten eines
schwingungsfähigen Systems gilt auch für den elektrischen Schwingkreis.
Wenn der elektrische Schwingkreis von einer Wechselspannungsquelle getrieben wird, ergeben sich die gleichen
Phänomene wie bei einem getriebenen Pendel, also auch eine Resonanz.
Anwendungen
- Schwingkreise zur Signalfilterung in Radioempfängern
- Verhalten von langen Leitungen
- Verhalten elektrischer Maschinen





Next: Elektromotoren
Up: Das Faradaysche Induktionsgesetz
Previous: Kirchhoffsche Gesetze
Contents
Index
Marti
2011-10-13

![\includegraphics[width=0.3\textwidth]{magnetismus-009}](img1181.gif)
![]() . Zu jedem Zeitpunkt muss die
Spannung im Stromkreis insgesamt null sein. Also ist
. Zu jedem Zeitpunkt muss die
Spannung im Stromkreis insgesamt null sein. Also ist
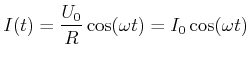
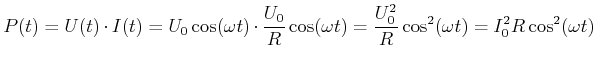
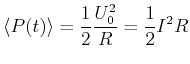
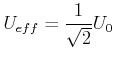
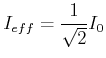
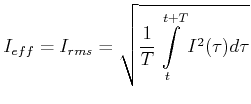
![\includegraphics[width=0.3\textwidth]{magnetismus-010}](img1194.gif)
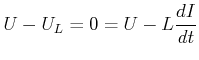
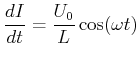
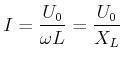
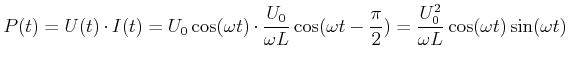
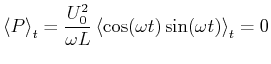
![\includegraphics[width=0.3\textwidth]{magnetismus-011}](img1205.gif)
![]() . Diese Spannung muss gleich der treibenden Spannung sein.
. Diese Spannung muss gleich der treibenden Spannung sein.
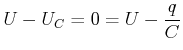
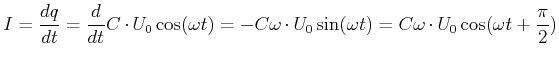
![\includegraphics[width=0.3\textwidth]{magnetismus-012}](img1215.gif)
![]() auf die Spannung
auf die Spannung ![]() aufgeladen sein. Zur Zeit
aufgeladen sein. Zur Zeit ![]() wird der Schalter
geschlossen. Die Differentialgleichung dieser Schaltung lautet:
wird der Schalter
geschlossen. Die Differentialgleichung dieser Schaltung lautet:
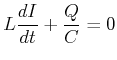
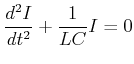
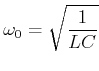
![\includegraphics[width=0.3\textwidth]{magnetismus-013}](img1220.gif)