


Licht ist eine transversale elektromagnetische Welle.
Das heisst, dass das elektrische und das magnetische
Feld senkrecht zur Ausbreitungsrichtung schwingen. Die
Wellengleichung für das elektrische Feld und damit auch für
Licht ist durch 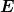 (
(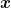 ,t) =
,t) = 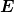 0(
0(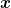 ) cos(
) cos(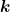 (
(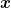 )·
)·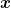 - ωt) gegeben.
Die Tatsache, dass wir eine Transversalwelle haben erfordert,
dass
- ωt) gegeben.
Die Tatsache, dass wir eine Transversalwelle haben erfordert,
dass 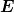 0 der Bedingung
0 der Bedingung
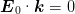 | (4.1) |
gilt.
Wenn wir nun, ohne Einschränkung der Allgemeinheit, die Ausbreitungsrichtung der Welle in die x-Richtung legen, dann sind
Diese Wahl erfüllt die Bedingung der Transversalität.
| Es gibt zwei mögliche orthogonale
Orientierungen von 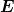 0 sowie die daraus
folgenden Linearkombinationen. Die Richtung,
in die 0 sowie die daraus
folgenden Linearkombinationen. Die Richtung,
in die 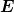 0 zeigt ist die Polarisationsrichtung. 0 zeigt ist die Polarisationsrichtung. |

__________________________________________________________________________
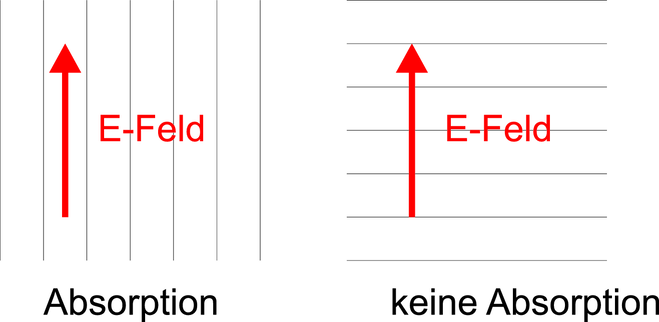
Polarisation durch Absorption in einem Drahtpolarisator
_____________________________________________________________________
Wenn das elektrische Feld einer Mikrowellen entlang eines Drahtes zeigt, kann dieses Feld im Draht Ladungen bewegen und so Energie abgeben. Die Intensität der Welle und damit die die Absorption hängen von der Polarisation ab.
Ebenso gibt es Moleküle mit Doppelbindungen zwischen den Kohlenstoffatomen, bei denen π-Elektronen beweglich sind, die wie Drähte wirken. Werden diese Moleküle orientiert zu einer Folie gemacht, so erhält man eine polarisierende Folie.
__________________________________________________________________________
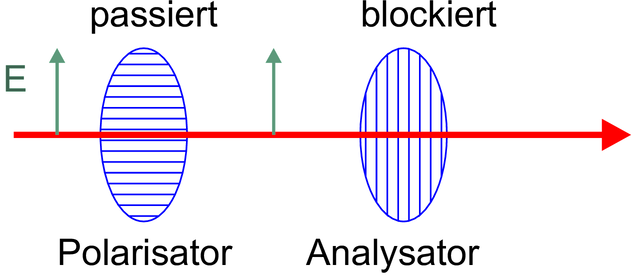
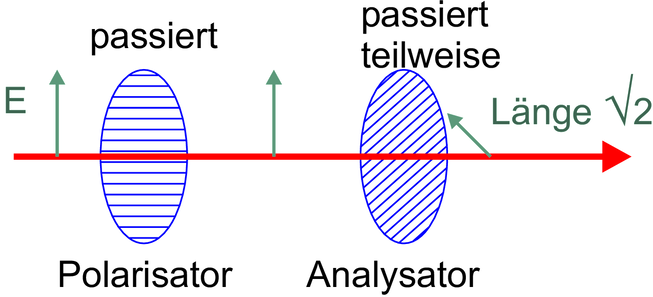
Licht durch einen Polarisator und einen Analysator mit gekreuzten Polarisationsrichtungen. Darunter die gleiche Anordnung, aber der Analysator ist nun um π∕4 gedreht.
_____________________________________________________________________
Bei einer Anordnung von Analysator und Polarisator
polarisiert der Polarisator das Licht. Der Analysator lässt nur
die Projektion des 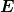 -Feldes auf seine Durchlassachse durch.
Für die Amplitude gilt
-Feldes auf seine Durchlassachse durch.
Für die Amplitude gilt
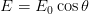 | (4.2) |
wobei θ der Winkel zwischen den Polarisationsrichtungen
von Polarisator und Analysator ist. Da die Intensität durch
I = 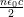 E2 ist und somit proportional zum Quadrat der
Amplitude I ∝ E2, gilt für die Intensität
E2 ist und somit proportional zum Quadrat der
Amplitude I ∝ E2, gilt für die Intensität
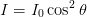 | (4.3) |
(Gesetz von Malus). Wenn zwischen gekreuzten Polarisatoren und Analysatoren eine optisch aktive Substanz eingebracht wird, kann mit dieser Anordnung die Grösse der optischen Aktivität gemessen werden3 .
__________________________________________________________________________

Dichroismus in einem NaV O4Mn-Kristall (gezüchtet von A. Lentz, fotographiert von M. Pietralla).
_____________________________________________________________________

 | Versuch zur Vorlesung: |
| Sonnenuntergang (Versuchskarte O-042) | |
_______________________________________________
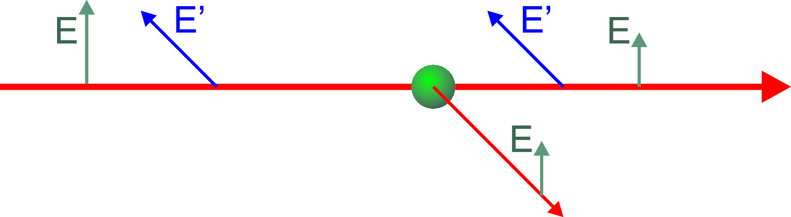
Polarisation durch Streuung an einem Teilchen
_____________________________________________________________________
Wenn Licht von links auf ein streuendes Teilchen (z.B. ein
Wassertröpfchen) fällt, dann kann nur die Komponente des
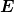 -Feldes, die auch senkrecht zur Streurichtung steht, eine
Lichtwelle anregen. Die dazu senkrechte Komponente würde
eine propagierende, longitudinal polarisierte Welle erzeugen.
Propagierende, longitudinale Lichtwellen stehen aber im
Widerspruch zu den Maxwellschen Gleichungen und treten
deshalb nicht auf.
-Feldes, die auch senkrecht zur Streurichtung steht, eine
Lichtwelle anregen. Die dazu senkrechte Komponente würde
eine propagierende, longitudinal polarisierte Welle erzeugen.
Propagierende, longitudinale Lichtwellen stehen aber im
Widerspruch zu den Maxwellschen Gleichungen und treten
deshalb nicht auf.

 | Versuch zur Vorlesung: |
| Spiegelanalysator (Versuchskarte O-115) | |
_______________________________________________
_____________________________________________________________________
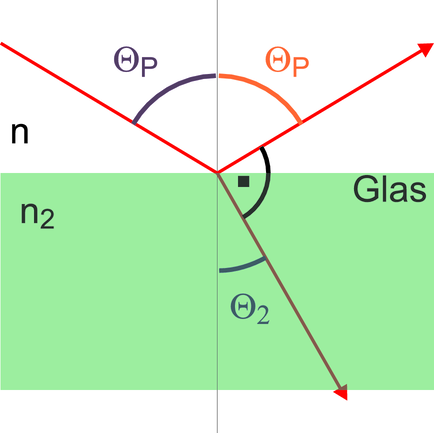
Wenn Licht in ein dichteres Medium eindringt und es zur Reflexion (Siehe Abschnitt 4.2) und zur Brechung kommt gelten zwei Gesetze
Wenn nun der Winkel zwischen dem gebrochenen Licht und
dem reflektierten Licht π∕2 ist, haben wir wieder die Situation
wie bei der Streuung: im reflektierten Licht kann keine
Lichtwelle angeregt werden, deren Polarisationsrichtung (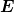 !)
in der durch den einfallenden und gebrochenen Lichtstrahl
definierten Einfallsebene liegt. Das heisst, der reflektierte
Strahl ist vollkommen polarisiert mit der Polarisationsebene
senkrecht zur Einfallsebene. Der Winkel θP heisst nach seinem
Entdecker Brewster-Winkel. Eine Betrachtung der Winkel in
der Abbildung ergibt, dass θP + θ2 = π∕2 ist. Damit wird der
Brewster-Winkel
!)
in der durch den einfallenden und gebrochenen Lichtstrahl
definierten Einfallsebene liegt. Das heisst, der reflektierte
Strahl ist vollkommen polarisiert mit der Polarisationsebene
senkrecht zur Einfallsebene. Der Winkel θP heisst nach seinem
Entdecker Brewster-Winkel. Eine Betrachtung der Winkel in
der Abbildung ergibt, dass θP + θ2 = π∕2 ist. Damit wird der
Brewster-Winkel
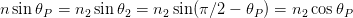 | (4.4) |
und damit
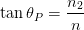 | (4.5) |
Für Glas (n2 = 1.5) gegen Luft (n = 1) ist θP = arctan(1.5) = 0.3128π = 56.310. Der Brewster-Winkel wird zum Beispiel beim Resonator von Gaslasern angewandt um die Polarisationsrichtung zu definieren.

 | Versuch zur Vorlesung: |
| Doppelbrechung (Versuchskarte O-005) | |
Viele Materialien haben isotrope optische Eigenschaften. Analog zu den elastomechanischen Eigenschaften von isotropen Materialien, die durch den Elastizitätsmodul E beschrieben werden, werden isotrope optische Materialien durch eine Brechzahl n = ε2 beschrieben. Die mechanischen Eigenschaften anisotroper Materialien werden durch Tensoren beschrieben. Analog werden optische Eigenschaften anisotroper Medien durch Tensoren ε oder n beschrieben. Die Mathematik sagt, dass solche Tensoren in einem Hauptachsensystem nur Komponenten auf ihren Hauptdiagonalen haben. Für den Brechungsindex heisst dies, dass nicht einer, n sondern drei Indizes n1, n2 und n3 angegeben werden müssen.
___________________________________________________________________________
| Material | Anwendung |
| Kalkspat | |
| Quarz | |
| Flüssigkristalle | Anzeigen ... |
| Plexiglas unter
mechanischer
Spannung | Spannungsuntersuchung |
| usw. | |
_____________________________________________________________________
_____________________________________________________________________
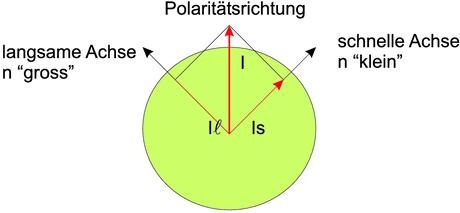
Wirkungsweise eines λ∕4-Plättchens oder eines λ∕2-Plättchens
_____________________________________________________________________
Bei einem λ∕4- oder einem λ∕2-Plättchen wird die Polarisationsrichtung des einfallenden Lichtes so gewählt, dass sie π∕4 zu den beiden Hauptachsen mit nschnell < nlangsam ist. Dann wird die eine Welle wie in der unten stehenden Zeichnung gezeigt, langsamer propagiert als die andere (die rote). Es entsteht eine Phasenverschiebeung, die bei λ∕4-Plättchen gerade eine viertel Wellenlänge ausmacht. Das Licht ist dann zirkular polarisiert.
__________________________________________________________________________
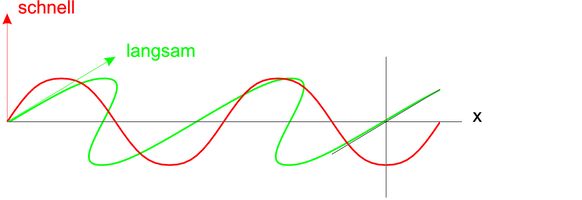
Wellen in einem λ∕4-Plättchen
_____________________________________________________________________
Ist der Gangunterschied λ∕2, wie in der oben stehenden Zeichnung, dann wird die Polarisationsrichtung um π∕2 gedreht.
Wir beschreiben kohärentes Licht durch die Gleichung
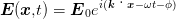 | (4.6) |
wobei 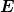 0·
0·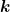 = 0 ist (Transversalität) und
= 0 ist (Transversalität) und 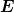 0 die
Polarisationsrichtung angibt. ϕ ist die Phase, die die
Anfangsbedungung am Ort 0 und zur Zeit 0 angibt.
0 die
Polarisationsrichtung angibt. ϕ ist die Phase, die die
Anfangsbedungung am Ort 0 und zur Zeit 0 angibt.
Ohne Einschränkung der Allgemeinheit können wir
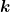 = (k; 0; 0) setzen. Dann ist
= (k; 0; 0) setzen. Dann ist 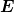 0 = (0; Ey; Ez) die möglichen
Polarisationsrichtungen. Der Vektor des elektrischen Feldes
hat also nur Komponenten in die y- und die z-Richtung.
0 = (0; Ey; Ez) die möglichen
Polarisationsrichtungen. Der Vektor des elektrischen Feldes
hat also nur Komponenten in die y- und die z-Richtung.
Unser dichroitisches Plättchen habe die schnelle Achse (Brechungsindex n1) entlang y′ und die langsame Achse (Brechungsindex n2) entlang z′ und die Dicke ℓ. Die x-Achse sollen übereinstimmen. Das gestrichene Koordinatensystem sei um den Winkel α gegen das ungestrichene verdreht. Dann ist
| x′ | = x | ||
| y′ | = y cos(α) - z sin(α) | ||
| z′ | = y sin(α) + z cos(α) | (4.7) |
Für Licht mit einer beliebigen Polarisation und einer Ausbreitung entlang der x-Achse muss das elektrische Feld auf das gestrichene Koordinatensystem projiziert werden. Am Anfang des Plättchens sei zudem die Phase ϕ = 0. Wir bekommen dann
| Ey′ | = Ey cos α - Ez sin α | ||
| Ez′ | = Ey sin α + Ez cos α | (4.8) |
Die Feldkomponente mit der Polarisation Ey′ breitet sich
mit der Geschwindigkeit c1 = c∕n1 aus, die Polarisation
Ez′ mit der Geschwindigkeit c2 = c∕n2. Damit sind die
Wellenlängen der Polarisation entlang y′ λ1 = λ∕n1 = 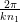 =
= 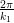 und entlang z′ λ2 = λ∕n1 =
und entlang z′ λ2 = λ∕n1 = 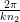 =
= 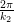 . Für die
. Für die 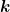 gilt
dann
gilt
dann
| k1 | = n1k | ||
| k2 | = n2k | (4.9) |
Die Laufzeit durch ein Plättchen der Dicke ℓ ist dann t1 = ℓ∕c1 = ℓn1∕c und t2 = ℓ∕c2 = ℓn2∕c. Wir betrachten zu einer feststehenden Zeit (praktischerweise t = 0) das Wellenmuster. Am Ausgang des Plättchens haben wir
| Ey′(ℓ,0) | = Ey′eik1ℓ = E y′ein1kℓ | ||
| Ez′(ℓ,0) | = Ez′eik2ℓ = E y′ein2kℓ | (4.10) |
Der Phasenunterschied der beiden Wellen ist die Differenz der Argumente der Exponentialfunktion, also ϕ(ℓ)(n2 -n1)kℓ Wir können also auch schreiben
| Ey′(ℓ,0) | = Ey′ein1kℓ | ||
| Ez′(ℓ,0) | = Ez′ein1kℓeiϕ(ℓ) | (4.11) |
Wenn wir den gemeinsamen Faktor abspalten, dann wird die z′-Komponente gegen der y′-Komponente um ϕ(ℓ) phasenverschoben. Diese neuen Polarisationen müssen wir auf das x,y,z-Koordinatensystem mit
| x | = x′ | ||
| y | = y′ cos(α) + z′ sin(α) | ||
| z | = -y′ sin(α) + z′ cos(α) | (4.12) |
projizieren. Damit ist
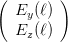 | = 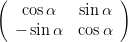 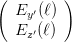 | ||
= 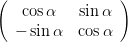 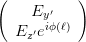 | |||
= 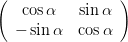 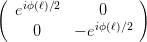 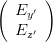 | (4.13) | ||
= 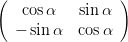 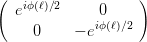 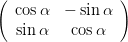 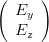 |
Ausmultipliziert erhält man für die Matrix
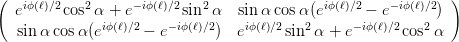 | (4.14) |
oder (nur für die Matrix)
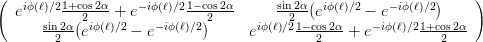 | (4.15) |
Wir vereinfachen und erhalten die Matrix
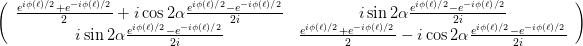 | (4.16) |
und erhalten
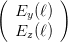 = = | |||||
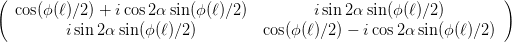 | |||||
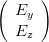 | (4.17) |
Wir betrachten nun den Spezialfall, dass α = π∕4 und ϕ(ℓ) = π∕2 ist. Die obige Matrix wird dann
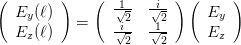 | (4.18) |
oder
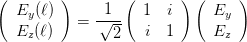 | (4.19) |
Eine Lichtwelle, die nur in y-Richtung polarisiert ist, wird zu einer Welle, die sowohl in die y wie auch in die z-Richtung polarisiert ist, aber mit einem Phasenfaktor von π∕2. Die Wellengleichung ist dann
| Ey(x,t) | = Ey cos(kx - ωt) | ||
| Ez(x,t) | = Ez cos(kx - ωt - π∕2) = Ez sin(kx - π∕2) | (4.20) |
Diese Art Wellen heisst zirkular polarisierte Welle. Es gibt zwei Arten, mit rechtsläufigem und linksläufigem Drehsinn. Ein dichroitisches Objekt, dass die obigen Eigenschaften hat, heisst λ∕4-Plättchen.
__________________________________________________________________________
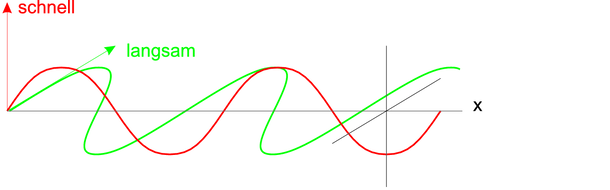
Wellen in einem λ∕2-Plättchen
_____________________________________________________________________
Der zweite wichtige Spezialfall ist α = π∕4 und ϕ(ℓ) = π. Die obige Matrix wird dann
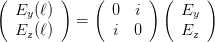 | (4.21) |
Licht mit einer Polarisationsrichtung in y-Richtung wird in Licht mit einer Polarisationsrichtung z überführt. Eine solche Anordnung heisst λ∕2-Plättchen. Zwei λ∕4-Plättchen hintereinander geschaltet haben die gleiche Wirkung. Anwendung: optisches Lesesystem in CDs.

Wir wollen in diesem Abschnitt mögliche Darstellungen des Polarisationszustandes des Lichtes beschreiben. Die Darstellung in diesm Abschnitt und den folgenden Unterabschnitten folgt Perez [Pér96].
Ohne Einschränkung der Allgemeinheit können wir annehmen, dass Licht sich entlang der x-Achse in einem kartesischen Koordinatensystem ausbreitet. Licht wird dann durch
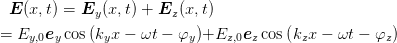 | (4.22) |
mit ky dem Wellenvektor der Welle mit einem elektrischen Feld in die y-Richtung. kz ist analog definiert. Durch eine Verschiebung der Zeitachse kanne rreicht werden, dass φy = 0 ist. Nur die Differenz der der Phasen ϕ = φy - φz = -φz ist relevant. Gleichung (4.22) lautet dann
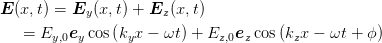 | (4.23) |
Mit dem Additionstheorem cos(α +β) = cos α cos β -sin α sin β erhalten wir
![E (x,t) = Ey (x, t) + Ez (x,t)
= Ey,0ey [cos (kyx)cos (ωt ) + sin(kyx )sin (ωt)]
+ Ez,0ez [cos (kzx)cos (ωt - ϕ) + sin (kzx)sin(ωt - ϕ )]](op-2015-2016195x.png) | (4.24) |
Wir können die Welle aus Gleichung (4.24) an irgend einem Ort untersuchen, z.B. bei x = 0. Dann lautet Gleichung (4.24)
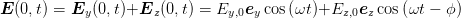 | (4.25) |
Gleichung (4.25) beschreibt eine Ellipse. Die folgende Abbildung 4.5.5 zeigt verschiedene Kurven als Funktion der Phasenverschiebung ϕ.
__________________________________________________________________________
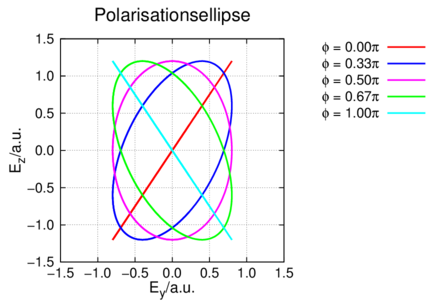
Gezeigt wird die Abhängigkeit von der Phase ϕ. Die Werte sind ω = 1, Ey,0 = 0.8 und Ez,0 = 1.2.
_____________________________________________________________________
Im Laborsystem ist die Ellipse durch
| Ey(t) | = Ey,0 cos 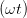 | Ez(t) | = Ez,0 cos 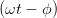 | (4.26) |
| und | ||||
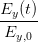 | = cos 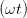 | 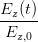 | = cos 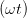 cos cos 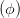 + sin + sin 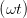 sin sin 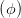 | (4.27) |
beschrieben, wobei ein Additionstheorem für den cos angewandt wurde. Wir setzen cos(ωt) in die zweite Gleichung ein und erhalten
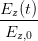 | = 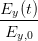 cos cos 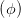 + + 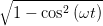 sin sin 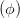 | ||
= 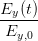 cos cos 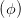 + + 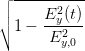 sin sin 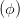 | (4.28) | ||
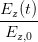 - -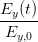 cos cos 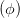 | = 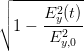 sin sin 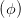 | ||
| und | |||
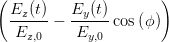 2 2 | = 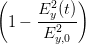 sin 2 sin 2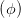 | (4.29) | |
Wird die Gleichung (4.29) neu geordnet, bekommen wir
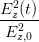 + + 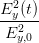 cos 2 cos 2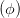 - 2 - 2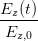 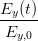 cos cos 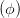 | = sin 2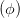 - -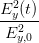 sin 2 sin 2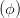 | (4.30) |
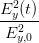 + + 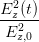 - 2 - 2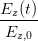 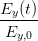 cos cos 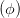 | = sin 2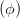 | (4.31) |
Nach Bronstein [?, p. 212, Kurven 2. Ordnung] kann bei einer Kurve vom Typ ax2 + 2bxy + cy2 = f der Typ der Kegelschnittkurve bestimmt werden, wenn die folgenden Kennzahlen berechnet werden:
| Δ | = 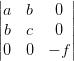 | δ | = 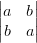 | S | = a + c | (4.32) |
berechnet werden. Für Δ ⇔ 0, δ > 0 und Δ·S < 0 beschreibt die Kurve eine Ellipse. Wir haben mit den Koeffizienten aus Gleichung (4.31)
| Δ | = 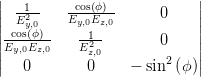 | = -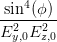 | (4.33) | |
| δ | = 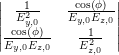 | = 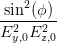 | (4.34) | |
| S | = 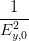 + + 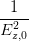 | (4.35) |
Da alle Koeffizienten reell sind, haben wie für ϕ ⇔ πn, n ∈ ℤ die Beziehungen Δ < 0 oder Δ ⇔ 0, δ > 0 und S·Δ < 0.
Ausser für ϕ ⇔ πn, n ∈ ℤ beschreibt das allgemeine
elektrische Feld 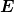 (t) eine Ellipse. Das heisst, dass es möglich
ist, diese Ellipse auf ihre Hauptachse zu transformieren. Eine
Ellipse wird in ihrem Hauptachsensystem durch
(t) eine Ellipse. Das heisst, dass es möglich
ist, diese Ellipse auf ihre Hauptachse zu transformieren. Eine
Ellipse wird in ihrem Hauptachsensystem durch
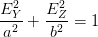 | (4.36) |
beschrieben, wobei a die Länge der grossen Hauptachse und
b die Länge der kleinen Hauptachse ist, also mit 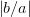 ≤ 1.
Das Vorzeichen von ϕ gibt den Drehsinn des elektrischen
Feldes.
≤ 1.
Das Vorzeichen von ϕ gibt den Drehsinn des elektrischen
Feldes.
Für ϕ = πn, n ∈ℤ haben wir lineare Polarisation, das heisst nach (4.31)
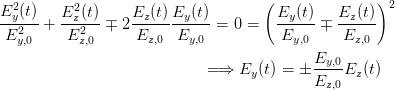 | (4.37) |
__________________________________________________________________________
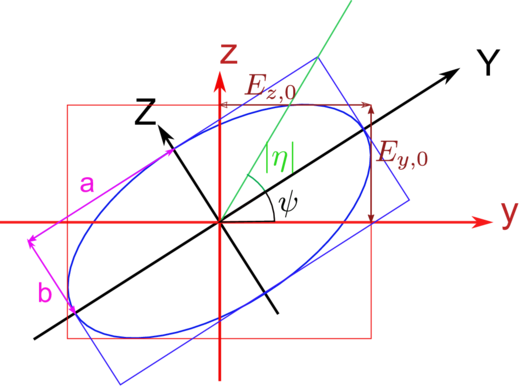
Koordinatensysteme zur Berechnung der elliptischen Polarisation. Das Laborsystem wird mit kleinen (roten) Buchstaben bezeichnet, das Eigensystem der Ellipse mit grossen (schwarzen) Buchstaben. Die weiteren Variablen werden im Text erklärt.
_____________________________________________________________________
Im Folgenden wollen wir die Darstellung der vom elektrischen
Feld abgefahrenen Ellipse in ihrem Hauptachsensystem
und im Laborsystem vergleichen. Das Laborsystem wird
durch die Einheitsvektoren  y und
y und  z aufgespannt, das
Hauptachsensystem durch
z aufgespannt, das
Hauptachsensystem durch  Y und
Y und  Z. In den beiden
Systemen lauten die Gleichungen für die Ellipse (siehe auch
Abbildung 4.5.5)
Z. In den beiden
Systemen lauten die Gleichungen für die Ellipse (siehe auch
Abbildung 4.5.5)
| Ey(t) | = Ey,0 cos 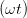 | EY (t) | = a cos 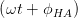 | (4.38) |
| Ez(t) | = Ez,0 cos 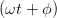 | EZ(t) | = b cos 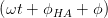 | (4.39) |
| ELabor(t) | = Ey(t) y + Ez(t) y + Ez(t) z z | EHS(t) | = EY (t) Y + EZ(t) Y + EZ(t) Z Z | (4.40) |
mit  y·
y· z = 0 und
z = 0 und  Y ·
Y · Z = 0. Die Intensität, gemittelt
über die Zeit ist
Z = 0. Die Intensität, gemittelt
über die Zeit ist
| ILabor | = 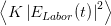 = K = K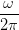 ∫
02π∕ω ∫
02π∕ω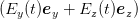 2dt 2dt | ||
= K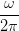 ∫
02π∕ω ∫
02π∕ω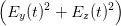 dt dt | |||
= K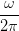 ∫
02π∕ω ∫
02π∕ω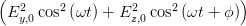 dt dt | |||
= K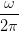 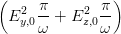 = = 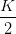 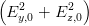 | (4.41) |
| IHS | = 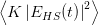 = K = K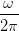 ∫
02π∕ω ∫
02π∕ω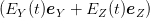 2dt 2dt | ||
= K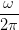 ∫
02π∕ω ∫
02π∕ω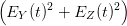 dt dt | |||
= K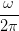 ∫
02π∕ω ∫
02π∕ω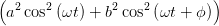 dt dt | |||
= K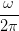 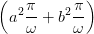 = = 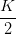 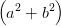 | (4.42) |
Dabei ist K eine (vom Einheitensystem abhängige) Konstante.
Also haben wir die Beziehung
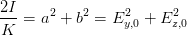 | (4.43) |
Im Hauptachsensystem lautet die Ellipsengleichung
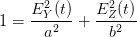 | (4.44) |
Diese transformieren wir jetzt in das Laborsystem mit der Drehmatrix
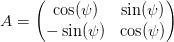 | (4.45) |
Damit haben wir die Beziehungen
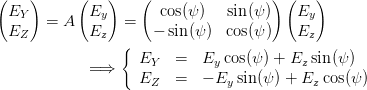 | (4.46) |
Wir setzen nun Gleichung (4.46) in Gleichung (4.44) ein und erhalten
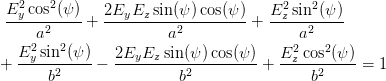 | (4.47) |
Wir fassen ähnliche Terme in Gleichung (4.47) zusammen und können diese Gleichung so mit Gleichung (4.31) vergleichen
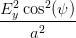 | + 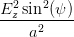 + + 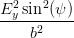 + + 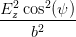 | ||
+ 2EyEz sin(ψ) cos(ψ)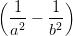 = 1 = 1 | (4.48) | ||
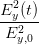 | + 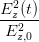 - 2 - 2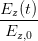 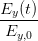 cos cos 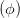 = sin 2 = sin 2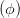 | (4.49) |
Der Vergleich der Gleichungen (4.48) und (4.49) ergibt die Beziehungen
Koeffizient von Ey2: 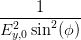 | = 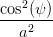 + + 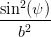 | (4.50) |
Koeffizient von Ez2: 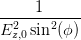 | = 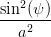 + + 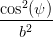 | (4.51) |
Koeffizient von EyEz: 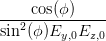 | = - cos(ψ) sin(ψ)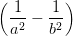 | (4.52) |
Die Addition von Gleichungen (4.50) und (4.51) ergibt
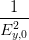 + + 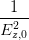 | = sin 2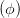 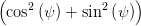 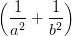 | ||
sin 2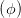 | = 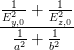 = = 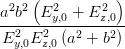 = = 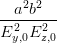 | (4.53) |
wobei Gleichung (4.43) verwendet wurde. Weiter erhalten wir aus Gleichung (4.53) mit Gleichung (4.43)
| ± ab | = Ey,0Ez,0 sin 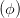 | (4.54) | |
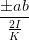 | = ±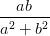 = ± = ±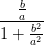 = = 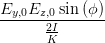 | ||
= 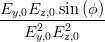 = = 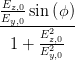 | (4.55) |
Wir definieren nun die Winkel (siehe Abbildung 4.5.5) mit Hilfe der Amplituden
tan 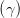 | := 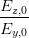 | tan 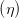 | := ±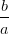 | (4.56) |
Weiter verwenden wir die Identität [?]
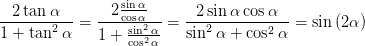 | (4.57) |
und erhalten mit der Gleichung (4.55) multipliziert mit 2
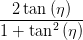 | = 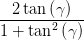 sin sin 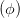 | ||
sin 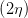 | = sin 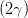 sin sin 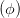 | (4.58) |
Eine weitere Beziehung gewinnen wir aus Gleichung (4.52) (mit sin(2α) = 2 sin α cos α) und Gleichung (4.54)
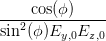 | = - sin sin 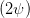 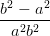 = = 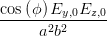 | ||
sin 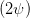 | = 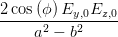 | (4.59) |
Wir suchen ψ(Ey,0,Ez,0,ϕ). Dazu müssen noch a2 und b2 eliminiert werden. Wir haben
| a2 - b2 | = 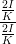 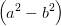 = = 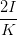 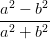 | ||
= 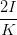 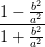 = = 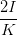 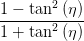 | |||
= 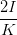 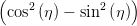 = = 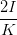 cos cos 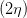 | (4.60) |
Andererseits folgt aus der Definition von γ und mit sin 2α = tan 2α∕(1 + tan 2α)
Ey,0 sin 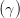 | = Ez,0 cos 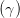 | ||
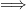 Ey,0 sin 2 Ey,0 sin 2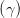 | = E
z,0 sin 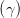 cos cos 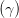 = =  Ez,0 sin Ez,0 sin 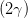 | ||
sin 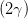 | = 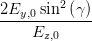 = = 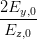 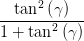 = = 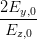 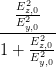 | ||
= 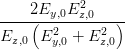 = = 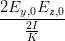 | (4.61) |
Weiter ist mit den Gleichungen (4.58) und (4.61)
| a2 - b2 | = 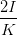 cos cos 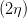 = = 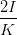  = = 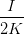 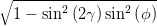 | ||
=  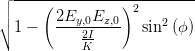 = 2 = 2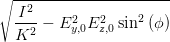 | |||
= 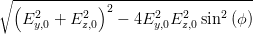 | (4.62) |
Damit lautet Gleichung (4.59)
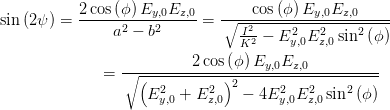 | (4.63) |
und mit Gleichung (4.43)
cos 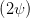 | = 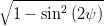 = = 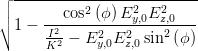 | ||
= 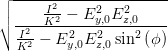 = = 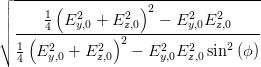 | |||
= 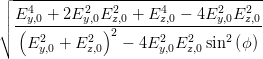 | |||
= 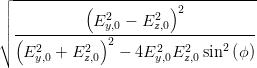 | |||
= 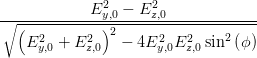 | (4.64) |
Aus den Gleichungen (4.63) und (4.64) bekommen wir
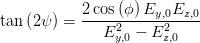 | (4.65) |
Damit sind alle Parameter in der Abbildung 4.5.5 bestimmt.

Wir haben eine Lichtwelle, die durch das elektrische Feld Ey,0 entlang der y-Achse, Ez,0 entlang der z-Achse und durch die Phase ϕ bestimmt ist. Da die y-und z-Achse orthogonal sind, kann man für die Gesamtintensität nach (4.41) auch schreiben
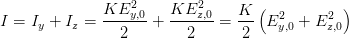 | (4.66) |
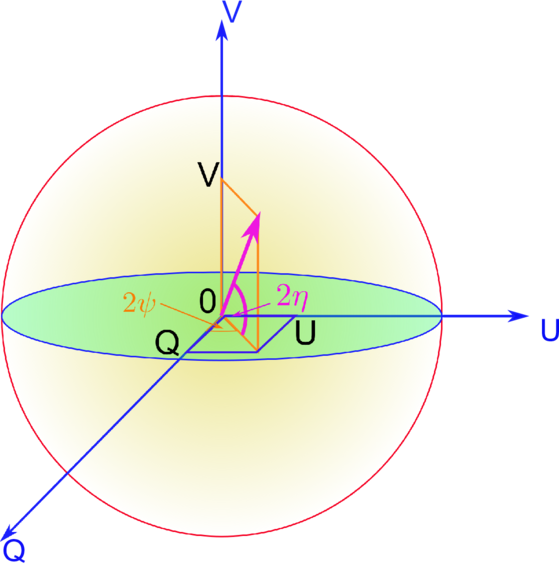
Dies ist der erste von drei Parametern nach Poincaré [?,
Kapitel 12]. Als zweiten Parameter verwendet Poincaré den
Winkel ψ = ∠( y,
y, Y ), also die Drehung der Ellipse. Der dritte
Parameter ist tan(η) = ±b∕a, also das Verhältnis der
Hauptachsen des vom elektrischen Felde beschriebenen
Ellipsoids. Wegen
Y ), also die Drehung der Ellipse. Der dritte
Parameter ist tan(η) = ±b∕a, also das Verhältnis der
Hauptachsen des vom elektrischen Felde beschriebenen
Ellipsoids. Wegen 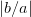 ≤ 1 ist auch
≤ 1 ist auch  ≤ π∕4.
≤ π∕4.
__________________________________________________________________________
_____________________________________________________________________
Poincaré hat deshalb die folgenden drei Parameter definiert (siehe auch Abbildung 4.5.5.1):
Die Definitionsbereiche der Winkel sind 0 ≤ ψ ≤ π (die Ellipse ist symmetrisch um die grosse Hauptachse) und -π∕4 ≤ η ≤ π∕4. Damit spannen die Gleichungen (4.67) eine Kugel auf.
Jeder Polarisationszustand zu einer Welle mit der Intensität I wird durch einen Punkt auf oder innerhalb der Kugel repräsentiert.
Weiter gilt:
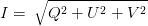 | (4.68) |
Welche Zustände gibt es auf der Poincaré-Kugel? Dazu schreiben wir mit Gleichung (4.66) die Gleichungen für sin(2ψ) (4.63), für cos((2ψ) (4.64) sowie für sin(2η) (4.58) und cos(2η) auf die Variablen Iy, Iz und ϕ um. Wir brauchen dazu noch Gleichung (4.56) und den ersten Teil von Gleichung (4.58).
sin 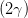 | = 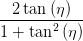 = = 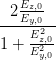 = = 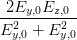 = = 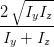 | (4.69a) | |
sin 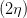 | = sin 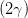 sin sin 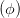 = = 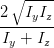 sin sin 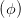 | (4.69b) | |
cos 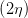 | = 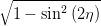 = = 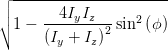 | ||
= 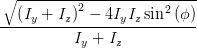 = = 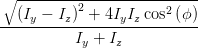 | (4.69c) | ||
sin 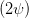 | = 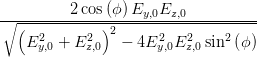 = = 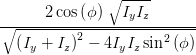 | ||
= 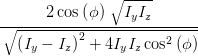 | (4.69d) | ||
cos 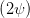 | = 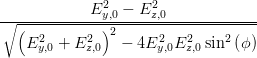 = = 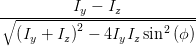 | ||
= 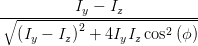 | (4.69e) |
Setzen wir (4.69) in (4.67) ein, erhalten wir
___________________________________________________________________________
| Polarisation | Iy | Iz | ϕ | Vektor (Q,U,V )∕I |
| Linear in y | I | 0 | 0 | (1, 0, 0) |
| Linear in z | 0 | I | 0 | (-1, 0, 0) |
| Linear 45° | I∕2 | I∕2 | 0 | (0, 1, 0) |
| Linear -45° | I∕2 | I∕2 | π | (0,-1, 0) |
| Zirkular links | I | I | π∕2 | (0, 0, 1) |
| Zirkular rechts | I | I | -π∕2 | (0, 0,-1) |
_____________________________________________________________________

Die Grössen Q, U und V können durch die Messung mit verschiedenen Polarisatorstellungen bestimmt werden.
__________________________________________________________________________
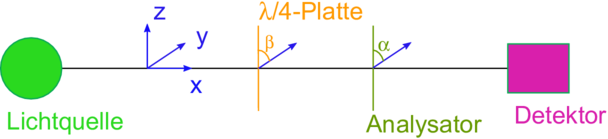
Messung der Stokes-Parameter.
_____________________________________________________________________
Wie Abbildung 4.5.5.2 zeigt braucht man zur Messung der Stokes-Parameter einen einstellbaren Analysator, eine drehbahre λ∕2-Platte und einen Detektor. Sei α der Winkel der Polarisationsebene des Analysators zur y-Achse, β der Winkel der Λ∕2-Platte zur y-Achse. Wir messen nun die Intensitäten bei α = 0 und β = 0, also I0,0, bei α = π∕4 und β = 0, also Iπ∕4,0, bei α = π∕4 und β = π∕4, also Iπ∕4,π∕4, bei α = π∕2 und β = 0, also Iπ∕2,0, α = 3π∕4 oder, was äquivalent ist bei α = -π∕4 und β = 0, also I-π∕4,0 und schliesslich bei α = -π∕4 und β = π∕4, also I-π∕4,π∕4.
Wir verwenden (4.27)
| Ey(t) | = Ey,0 cos 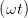 | Ez(t) | = Ez,0 cos 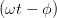 | (4.71) |
Ein Polarisator im Winkel α erzeugt eine Welle mit dem
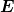 -Feld
-Feld
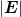 (α,t) (α,t) | = E(α,t) = Ey(t) cos(α) + Ez(t) sin(α) | ||
= Ey,0 cos 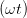 cos(α) + Ez,0 cos cos(α) + Ez,0 cos 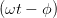 sin(α) sin(α) | (4.72) | ||
| (4.73) |
und damit bei einer Rechnung mit komplexen Wellen
Die Stokes-Parameter I, Q, U und V bekommen wir nun mit
| I | = Iy + Iz = I0,0 + Iπ∕2,0 | (4.80) |
| Q | = Iy - Iz = I0,0 - Iπ∕2,0 | (4.81) |
| U | = 2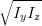 cos cos 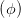 = Iπ∕4,π∕4 - I-π∕4,π∕4 = Iπ∕4,π∕4 - I-π∕4,π∕4 | (4.82) |
| V | = 2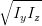 sin sin 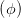 = I-π∕4,0 - Iπ∕4,0 = I-π∕4,0 - Iπ∕4,0 | (4.83) |
Es gibt noch weitere Möglichkeiten, durch die Messung der Intensitäten bei verschiedenen Polarisationsrichtungen den Polarisationszustand zu bestimmen (siehe z. B. Hecht [Hec05] oder Born und Wolf [?])
Müller 1948 [?] schlug vor, die Stokes-Parameter als Vektoren zu schreiben, also
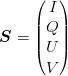 | (4.84) |
Damit werden ausgewählte Polarisationen (siehe auch Tabelle 4.5.5.1) geschrieben:
___________________________________________________________________________
| Polarisation | Stokes-Vektor | Polarisation | Stokes-Vektor |
| Linear in y | 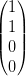 | Linear in z | 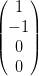 |
| Linear 45° | 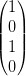 | Linear -45° | 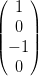 |
| Zirkular links | 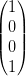 | Zirkular rechts | 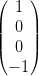 |
_____________________________________________________________________
Schliesslich verwendet man noch die Definition für den
Die Polarisation von Licht und deren Modifikation durch λ∕4 und λ∕2-Platten wird häufig mit Stokes-Vektoren und Müller-Matrizen beschrieben [?, Abschnitt 9.5]

Die Änderung der Polarisation von kohärentem Licht beim Durchgang durch Polarisatoren oder doppelbrechende Materialien kann mit Jones-Vektoren und Jones-Matrizen beschrieben werden. Jones-Vektoren und Jones-Matrizen sind eine Verallgemeinerung der obigen Rechnung. Formal läuft dies darauf hinaus, dass wir den Ausgangszustand als Vektor beschreiben und auf ihn die Operatoren der polarisationsändernden Objekte anwenden.
Aus der Darstellung im vorhergehenden Kapitel geht hervor, dass nur die y- und die z-Richtung die Polarisation beschreiben. Wir können also Zweiervektoren verwenden. Weiter soll die Phase der Welle als komplexe Zahl dargestellt werden. Schliesslich normieren wir die Länge des Vektors auf 1. Eine Welle polarisiert in die y-Richtung wird also durch den Vektor
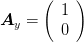 | (4.86) |
dargestellt. Rechtszirkular polarisiertes Licht wird durch
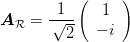 | (4.87) |
beschrieben.
| Jones-Vektoren | Beschreibung |
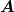 y = y = 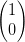 | Linear polarisiert in y-Richtung |
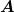 z = z = 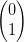 | Linear polarisiert in z-Richtung |
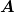 R = R = 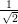 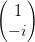 | Rechtshändig zirkular polarisiert |
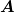 L = L = 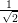 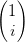 | Linkshändig zirkular polarisiert |
Polarisationen in andere Richtungen können durch die Anwendung von Drehmatrizen berechnet werden. Die Drehung aus dem Koordinatensystem y,z nach y′,z′ wird durch
| y′ | = y cos(α) - z sin(α) | ||
| z′ | = y sin(α) + z cos(α) | (4.88) |
beschrieben. Die Drehmatrix lautet also
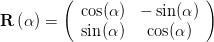 | (4.89) |
Ein um den Winkel α zu y-Achse linear polarisierter Strahl wird durch
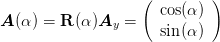 | (4.90) |
beschrieben. Ein linearer Polarisator in y-Richtung wird durch
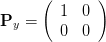 | (4.91) |
beschrieben. Die Wirkung eines um den Winkel α gedrehten Polarisators kann berechnet man, indem man das Koordinatensystem um -α dreht, den Polarisator in der y-Ebene anwendet und mit α zurückdreht.
| P(α) | = R(α)PyR(-α) | (4.92) | |
= 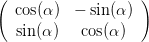 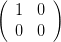 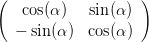 | |||
= 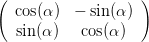 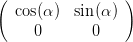 | |||
= 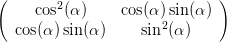 | (4.93) |
Die Jones-Matrix des linearen Polarisators in die z-Richtung lautet also
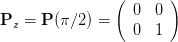 |
Die zirkulare Polarisation wird durch die beiden homogenen Polarisatoren PR und PL erzeugt.
| PR | =  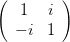 | (4.94) | |
| PL | =  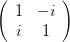 |
Das λ∕4 mit der schnellen Achse entlang der y-Richtung wird durch
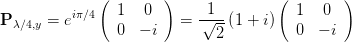 | (4.95) |
Mit der Gleichung (4.17) hatten wir ein schräg stehendes λ∕4-Plättchen berechnet. Die Gleichung ist aber allgemeiner: sie beschreibt ein Verzögerungselement von ϕ gedreht um α zur y-Achse.
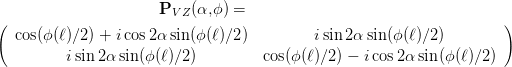 | (4.96) |
Das Verzögerungselement mit der schnellen Achse parallel zur y-Achse ist durch
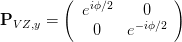 | (4.97) |
gegeben. Die folgende Tabelle zeigt aus Gleichung (4.96) berechenbaren Elemente.
| Jones-Matrix | Bedeutung |
Pλ∕4,y = eiπ∕4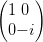 | λ∕4-Plättchen mit der schnellen Achse in y |
Pλ∕4,z = eiπ∕4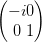 | λ∕4-Plättchen mit der schnellen Achse in z |
| Pλ∕4(α) = R(α)Pλ∕4,yR(-α) | λ∕4-Plättchen mit der schnellen Achse gedreht um α bezüglich y |
Pλ∕2,y = Pλ∕4,yPλ∕4,y =  | λ∕2-Plättchen mit der schnellen Achse in y |
Pλ∕2,z = Pλ∕4,zPλ∕4,z = 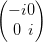 | λ∕2-Plättchen mit der schnellen Achse in z |
| Pλ∕2(α) = R(α)Pλ∕2,yR(-α) | λ∕2-Plättchen mit der schnellen Achse gedreht um α bezüglich y |
Wenn ein Lichtstrahl mit der Polarisation 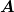 durch die
Objekte T1,T2,…,Tn geht, ist die resultierende Welle
durch die
Objekte T1,T2,…,Tn geht, ist die resultierende Welle
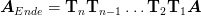 | (4.98) |
Mit den oben angegebenen Polarisations- und Rotationsmatrizen können die meisten Polarisationsprobleme berechnet werden.
(Siehe Gerthsen, Physik [?, pp. 535])
__________________________________________________________________________
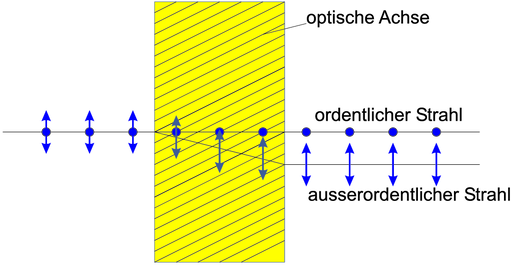
Aufspaltung eines Lichtstrahls in einem doppelbrechenden Material wie Kalkspat
_____________________________________________________________________
_____________________________________________________________________

Doppelbrechung in einem NaV O4Mn-Kristall (gezüchtet von A. Lentz, fotographiert von M. Pietralla). Gezeigt wird, dass die drei Kristallrichtungen eines sechseckig scheinenden Kristalls nicht äquivalent sind.
_____________________________________________________________________
Viele Kristalle sind nicht isotrop. Es gib auch in diesen
Kristallen Achsen, die eine höhere Symmetrie aufweisen, als die
anderen Achsen. Diese Achse wird Hauptachse genannt. Alle
physikalischen Eigenschaften eines Kristalls, also auch die
optischen Eigenschaften, müssen die Symmetrie des Kristalls
haben. Die physikalischen Eigenschaften und insbesondere die
Lichtgeschwindigkeit sind in allen Ebenen senkrecht zur
Hauptachse isotrop. Dabei ist die Lichtgeschwindigkeit aber
von der Polarisationsrichtung des Lichtes abhängig. In
Richtung der Hauptachse ist die Lichtgeschwindigkeit
unabhängig von der Polarisationsrichtung c0. Licht, das sich
senkrecht zur Polarisationsrichtung ausbreitet, bewegt sich
ebenfalls mit c0, wenn der  -Vektor in Richtung der
Hauptachse zeigt, die Polarisationsrichtung also senkrecht zur
Hauptachse liegt. Dieses licht heisst ordentliches Licht.
Licht mit der anderen Polarisationsrichtung läuft im
Kalkspat schneller, und zwar mit cao = 1.116c0. Dieses Licht
heisst ausserordentliches Licht. Wenn die Einfallsrichtung
dazwischen liegt, ist die Geschwindigkeit des ordentlichen
Lichts immer noch c0, die des ausserordentlichen Lichts liegt
zwischen c0 und cao.
-Vektor in Richtung der
Hauptachse zeigt, die Polarisationsrichtung also senkrecht zur
Hauptachse liegt. Dieses licht heisst ordentliches Licht.
Licht mit der anderen Polarisationsrichtung läuft im
Kalkspat schneller, und zwar mit cao = 1.116c0. Dieses Licht
heisst ausserordentliches Licht. Wenn die Einfallsrichtung
dazwischen liegt, ist die Geschwindigkeit des ordentlichen
Lichts immer noch c0, die des ausserordentlichen Lichts liegt
zwischen c0 und cao.
Die Wellenflächen des ordentlichen Lichts stammend von einer punktförmigen Quelle sind also Kugelflächen, während die Wellenflächen des ausserordentlichen Lichts Rotationsellipsoide sind, deren Rotationsachse mit der Hauptachse parallel ist. Bei Kalkspat ist das Rotationsellipsoid abgeplattet, das Material heisst einachsig negativ. Bei Quarz ist das Rotationsellipsoid länglich (die ordentliche Lichtgeschwindigkeit ist grösser als die ausserordentliche.). Man nennt Quarz deshalb einachsig positiv.
Wenn Licht senkrecht auf eine Fläche fällt, die schräg zur Hauptachse liegt, müssen zwei verschiedene Konstruktionen verwendet werden:
Da die resultierenden Flächen Tangentenflächen sind, bleibt die Richtung des ordentlichen Lichtes senkrecht zur Oberfläche, während das ausserordentliche Licht sich schräg weiter ausbreitet. Zur Berechnung des Lichtweges müssen Tensoren verwendet werden.
__________________________________________________________________________
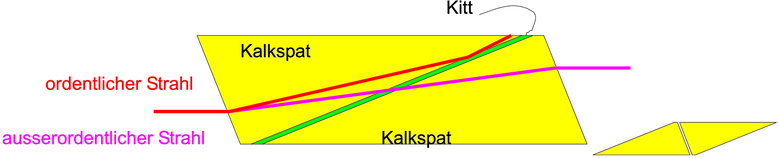
Das Nicolsche Prisma, kurz Nicol, ist eine Anwendung der Doppelbrechung zur Polarisation. Der spitze Winkel ist 680, der abgeflachte Winkel genau 900. Die optische Achse liegt senkrecht zur Längsachse in der Bildebene. Das Nicol-Prisma entsteht aus dem rechts gezeigten länglichen Kalkspatkristall, der diagonal geschnitten wird. Er wird mit einem Kitt, dessen Brechungsindex wie der Brechungsindex des ausserordentlichen Strahls ist, wieder zusammengeklebt. der ausserordentliche Strahl geht dann ohne grössere Ablenkung durch das Nicol-Prisma, während der ordentliche Strahl am Kitt totalreflektiert wird und aus dem Strahlengang verschwindet.
_____________________________________________________________________
In der Technik war die spannungsinduzierte Doppelbrechung lange das einzige Mittel, unzulässige Beanspruchungen in Bauteilen festzustellen.
 | Versuch zur Vorlesung: |
| Spannungsdoppelbrechung (Versuchskarte O-008) | |
 Lizenzinformationen
Lizenzinformationen