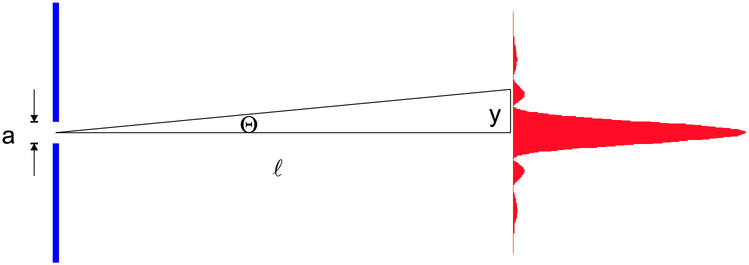
_______________________________________________
Berechnung des Beugungsmusters an einem Einzelspalt.
_____________________________________________________________________
| Literatur | |
In diesem Abschnitt wird die Beugung an einem Einzelspalt näherungsweise berechnet. Dabei verwenden wir die Methode, Phasen und Amplituden in der komplexen Ebene aufzuaddieren.
| Versuch zur Vorlesung: | |
| Beugung am Einzelspalt (Versuchskarte O-050) | |
_______________________________________________
Berechnung des Beugungsmusters an einem Einzelspalt.
_____________________________________________________________________
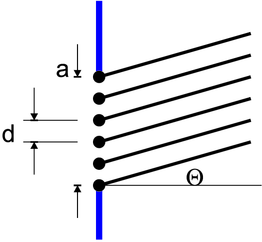
Wir definieren den Winkel Θ genau so wie in der Zeichnung
| Literatur | |
Wir betrachten N + 1 punktförmige Lichtquellen in einem Spalt der Breite a. Ihr Abstand ist d = a∕N. Der Phasenunterschied zwischen zwei Lichtquellen in die Richtung Θ ist
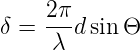 | (3.1) |
__________________________________________________________________________
_____________________________________________________________________
Der gesamte Phasenunterschied ist
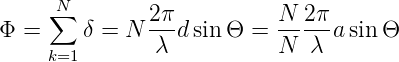 | (3.2) |
oder
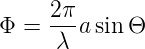 | (3.3) |
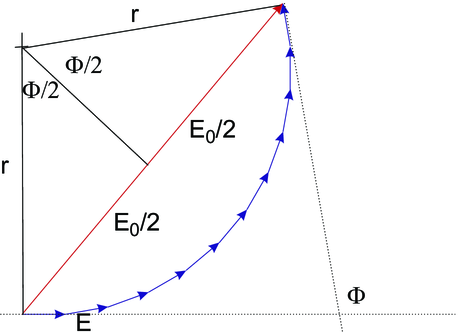
Wie hängt nun die Amplitude von Φ ab?
Die Amplitude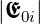 
resultiert aus der Addition von N + 1
Einzelamplituden E. Aus der Abbildung ist ersichtlich,
dass
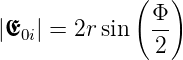 | (3.4) |
Für den Winkel Θ = 0 ist Emax = E(Φ = 0) = N·E. Die Amplituden der einzelnen Quellen sind unabhängig von der Beobachtungsrichtung. Deshalb ist auch die Bogenlänge Emax = N·E = rΦ. Wir lösen nach r auf und setzen ein.
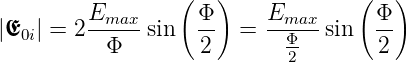 | (3.5) |
Wenn wir berücksichtigen, dass I =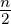 
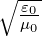E2 ist und wir
I0 =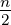 
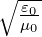Emax2 setzen, erhalten wir für die Intensität
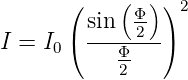 | (3.6) |
Wenn wir Φ einsetzen, bekommen wir
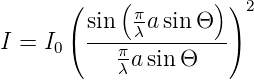 | (3.7) |
__________________________________________________________________________
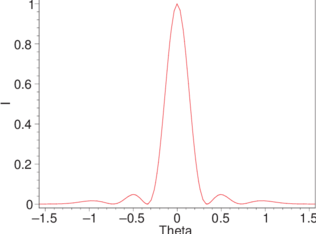
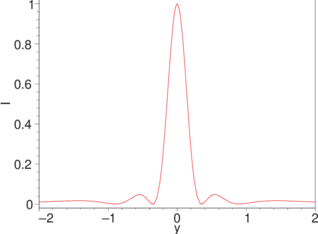
Beugungsmuster als Funktion des Ablenkwinkels und, rechts, als Funktion des Abstandes von der optischen Achse.
_____________________________________________________________________
Wir können mit Θ(y) = arctan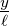 
das Beugungsmuster für
einen ebenen Schirm berechnen. Soll das Beugungsmuster in
Funktion von Θ betrachtet werden, muss es mit einer
Sammellinse (Schirm im Brennpunkt) betrachtet werden.
__________________________________________________________________________
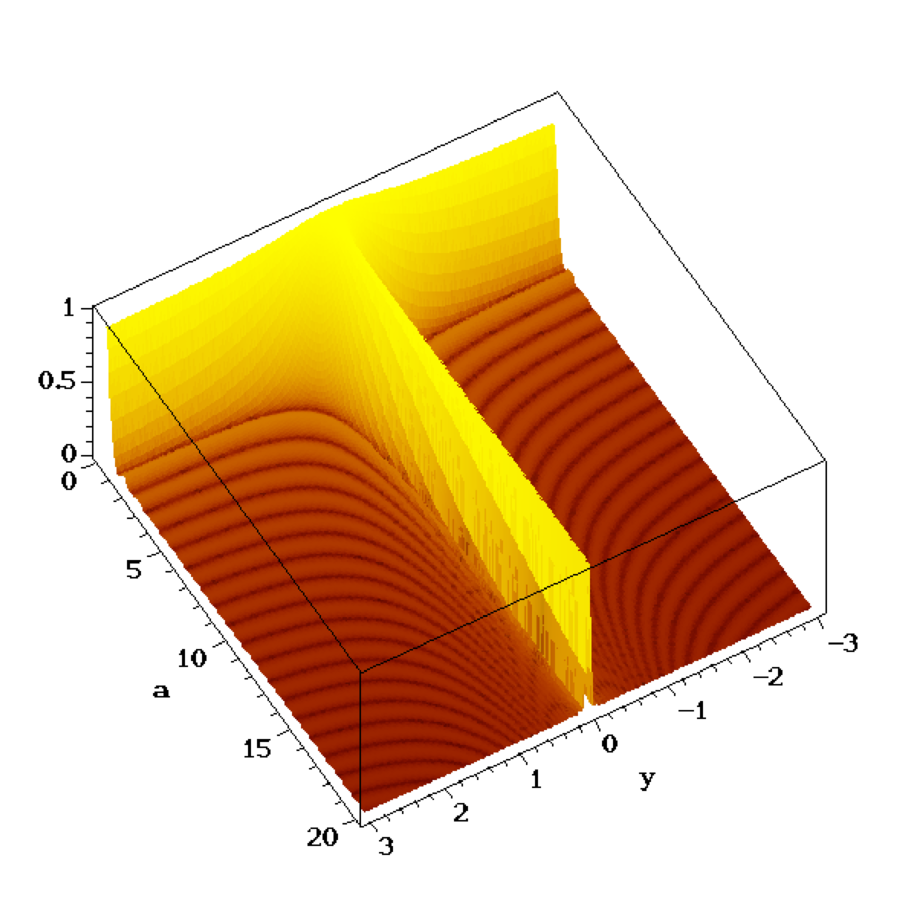
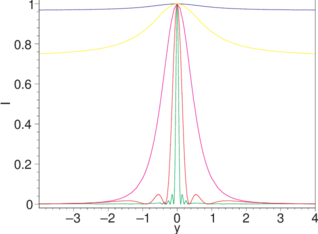
Beugungsmuster als Funktion der Spaltbreite. Links kontinuierlich und rechts für die Breiten a = 0.1,0.3,1,3,10
__________________________________________________________________________
Die Lage der Beugungsmaxima und -minima ist gegeben durch Φ∕2 = kπ, k = ±1,±2,… für die Minima und Φ∕2 = (k + 1∕2)π, k = ±1,±2… sowie Φ = 0 für die Maxima.
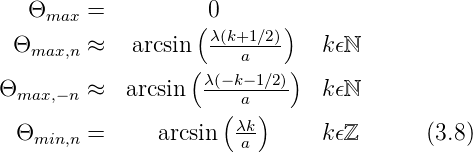
Die Amplitude in den Nebenmaxima Θmax,n bekommt man durch Ableitung und auf Null setzen. Ungefähr liegen diese Maxima in der Mitte zwischen den Minima. Die Amplitude ist dort ungefähr
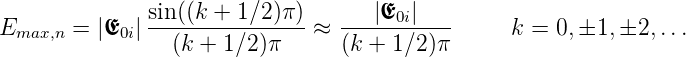 | (3.9) |
Damit gilt für die Intensitäten der Nebenmaxima
![I
Imax,n = ------0-----2 k = 0,±1, ±2,...
[(k + 1∕2 )π]](op-2016-2017395x.png) | (3.10) |
___________________________________________________________________________
| Φ∕2 | Art | Amplitude bezogen auf I0 |
| 0 | Maximum | 1 |
| ±π | Minimum | 0 |
| ≈±3π∕2 | Maximum | ≈ |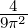
| ±2π | Minimum | 0 |
| ≈±5π∕2 | Maximum | ≈ |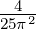
| ≈±7π∕2 | Maximum | ≈ |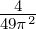
| ≈±9π∕2 | Maximum | ≈ |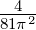
_____________________________________________________________________
Die genaue Lage der Extrema kann man durch
![[ ]2
-∂- sin(Φ-∕2) sin(Φ-∕2)cos(Φ-∕2)- sin2(Φ∕2-)
0 = ∂ Φ Φ∕2 = 4 Φ2 − 8 Φ3](op-2016-2017400x.png) | (3.11) |
oder vereinfacht für Φ ⇔ 0
![( ) [ ( ) ( ) ]
0 = sin Φ- Φ cos Φ- − 2 sin Φ-
2 2 2](op-2016-2017401x.png) | (3.12) |
bestimmt werden. Nullstellen gibt es für sin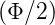 
= 0 und
für Φ cos 
− 2 sin 
= 0 oder
Dies folgt aus der Analyse der zweiten Ableitung
![2 [ ]2 2
-∂-- sin-(Φ∕2-) 2((Φ--−--6)cos(Φ)-−-4Φ-sin(Φ)-+-6)-
∂Φ2 Φ ∕2 = Φ4
Φ⇔0 ( )
= Φ2 − 6 cos(Φ) − 4Φ sin(Φ) + 6](op-2016-2017406x.png) | (3.14) |
Für Φ = 2kπ mit k ∈ ℤ∖{0} ist die zweite Ableitung positiv, es sind also Minima. Die anderen Lösungen müssen also Maxima sein.
Für grosse Beugungsordnungen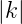 
→∞ geht die Lage der
Maxima gegen Φ = (2k − 1)π. In der Nähe der optischen
Achse sind sie verschoben.
Lizenzinformationen
