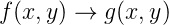

| Literatur | |
| Versuch zur Vorlesung: | |
| Auflösungsvermögen eines Mikroskops (Versuchskarte O-001) | |
Wir verwenden die Tatsache, dass optische Systeme in den einfachsten Fällen lineare Systeme sind und verwenden die in Abschnitt 3.3.3 eingeführte Fouriertransformation, hier aber in zwei Dimensionen. Wenn f(x,y) und g(x,y) Intensitätsverteilungen senkrecht zur optischen Achse sind, und f die Ausgangsverteilung und g die Bildverteilung ist, schreibt man für die Abbildung
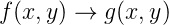 | (3.1) |
Die Abbildung ist linear, das heisst, wenn f1 →g1 und f2 →g2 ist, ist
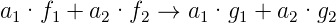 | (3.2) |
Wir nennen 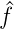 (u,v) die Fouriertransformation von f(x,y).
Im Zusammenhang mit der Fourieroptik ist die Bezeichnung
(u,v) die Fouriertransformation von f(x,y).
Im Zusammenhang mit der Fourieroptik ist die Bezeichnung
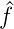 (
(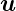 ) = F(
) = F(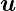 ) üblich, also keine Grossbuchstaben wie oftmals
verwendet. Es gilt
) üblich, also keine Grossbuchstaben wie oftmals
verwendet. Es gilt
![∬
f (x,y) = ^f(u,v)e2πi[ux+vy]dudv
∬
f^(u,v) = f(x,y)e− 2πi[ux+vy]dxdy (3.3)](op-2016-2017507x.png)
Wir schreiben 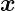 = (x,y) und
= (x,y) und 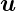 = (u,v) Die
Fouriertransformation lässt sich dann kompakt schreiben
als
= (u,v) Die
Fouriertransformation lässt sich dann kompakt schreiben
als
![∬
f(x ) = f^(u)e2πi[u·x ]du
∬
^f(u ) = f (x)e−2πi[u·x ]dx (3.4)](op-2016-2017510x.png)
| Literatur | |
| Versuch zur Vorlesung: | |
| Fourier-Transformation (Versuchskarte O-067) | |
Ein Lichtfleck an der Position 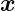 ′ der Eingangsebene erzeugt
eine Intensitätsverteilung in der Ausgangsebene, die sowohl
vom Beobachtungspunkt
′ der Eingangsebene erzeugt
eine Intensitätsverteilung in der Ausgangsebene, die sowohl
vom Beobachtungspunkt 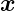 wie auch von
wie auch von 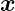 ′ abhängt. Die
Impulsantwort ist
′ abhängt. Die
Impulsantwort ist
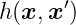 | (3.5) |
Ein optisches System ist translationsinvariant, wenn
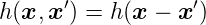 | (3.6) |
gilt. Bei einem kontinuierlichen linearen optischen System gilt zwischen der Bildebene und der Eingangsebene die Beziehung
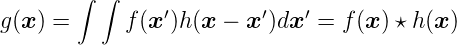 | (3.7) |
Dies ist das Faltungstheorem (Siehe auch Gleichung (3.3)) aus der Fourieroptik. Im Fourierraum wird aus einer Faltung eine Multiplikation, also
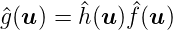 | (3.8) |
Wenn die optische Übertragung kohärent verläuft, dann verwendet man die oben definierte kohärente Übertragungsfunktion, die Amplituden verknüpft. Ist die Übertragung nicht kohärent, muss man mit Intensitäten rechnen.
__________________________________________________________________________
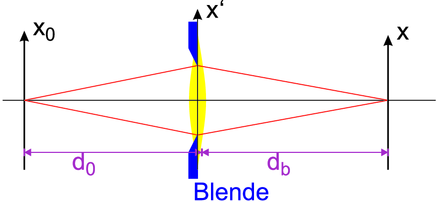
Berechnung der Beugung an einer Öffnung
_____________________________________________________________________
Das entstehende Beugungsbild eines Punktes ist das Fraunhofersche Beugungsmuster der Blendenöffnung. Die inkohärente Impulsantwort wird
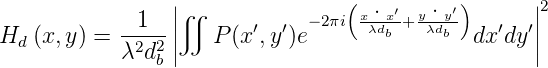 | (3.9) |
Dies bedeutet, dass Hd proportional zum Betragsquadrat der Fouriertransformation der Pupillenfunktion P ist.
Für eine kreisförmige Öffnung ist die Pupillenfunktion
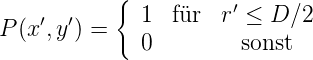 | (3.10) |
wobei D den Durchmesser der Öffnung und r′ = 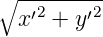 den Radius darstellt.
den Radius darstellt.
Die Rechnung ist in Polarkoordinaten einfacher.
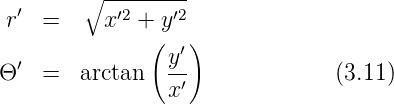
sowie in der Bildebene
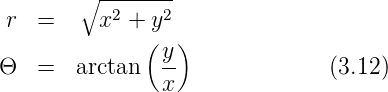
Mit ρb = r∕(λdb) bekommt man
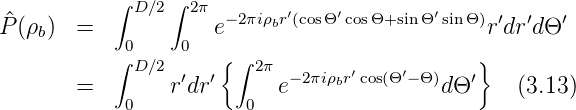
Dabei ist die Grösse
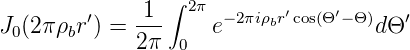 | (3.14) |
die sogenannte Besselfunktion nullter Ordnung. Die Fouriertransformation einer runden Pupille wird also
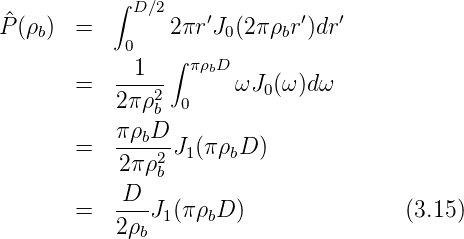
J1(α) = ∫ 0αωJ 0(ω)dω ist die Besselfunktion erster Ordnung. Mit r = λdbρb, Θ und S = πD2∕4, der Pupillenfläche, bekommt man für die komplexe Amplitude
![[ ]
^ 2J1-(πρbD-)
ψ (r) = P (ρb) = S πρbD
[ ]2
2 2 2J1(πρbD-)-
I(r) = K |ψ (r)| = KS π ρbD (3.16)](op-2016-2017526x.png)
Die Intensitäten als Funktion von X = ρbD sind
| X | 0 | 1.22 | 1.63 | 2.33 | 2.68 | 3.33 |
![[2J1(πX )∕ (πX )]](op-2016-2017527x.png) 2 2 | 1 | 0 | 0.017 | 0 | 0.004 | 0 |
_______________________________________________
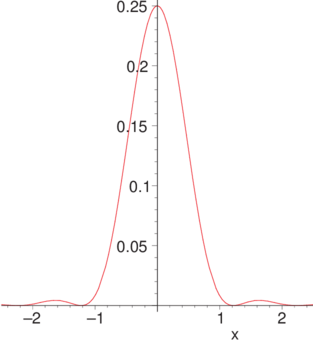
Die Beugung an einer ringförmigen Apertur.
_____________________________________________________________________
Bei der Beugungsfigur an einer kreisförmigen Öffnung mit
dem Durchmesser d ist das erste Minimum bei sin Θ = 1.22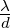 .
.
__________________________________________________________________________
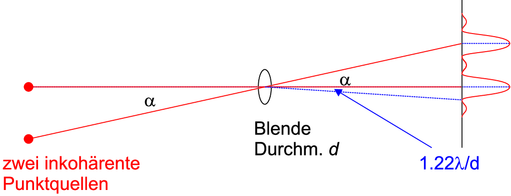
Abbildung zweier punktförmiger, inkohärenter Quellen durch eine Blende mit der Öffnung d.
_____________________________________________________________________
Bei dem sogenannten kritischen Winkel αK, der durch
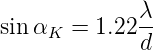 | (3.17) |
gegeben ist, fällt das Minimum der einen Beugungsfigur gerade auf das Maximum der anderen. Das obige Kriterium wird das Rayleighsche Auflösungskriterium genannt.
__________________________________________________________________________
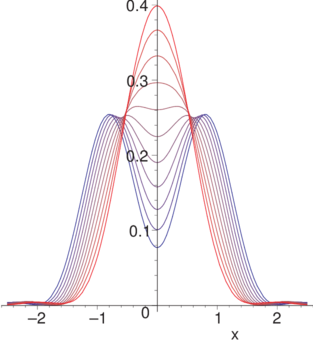
Form der Intensität bei der Überlagerung zweier inkohärenter Punktquellen. Der Abstand variiert von 0.6 (rot) bis 1.6 (blau) in Schritten von 0.1.
_____________________________________________________________________
Diese Abbildung zeigt, dass die Definition des Auflösungsvermögens an das mögliche Signal-Rausch-Verhältnis gebunden ist. Mit modernen Detektoren mit 16 Bit Auflösung sind deshalb leicht bessere Grenzen der Auflösung möglich.
__________________________________________________________________________
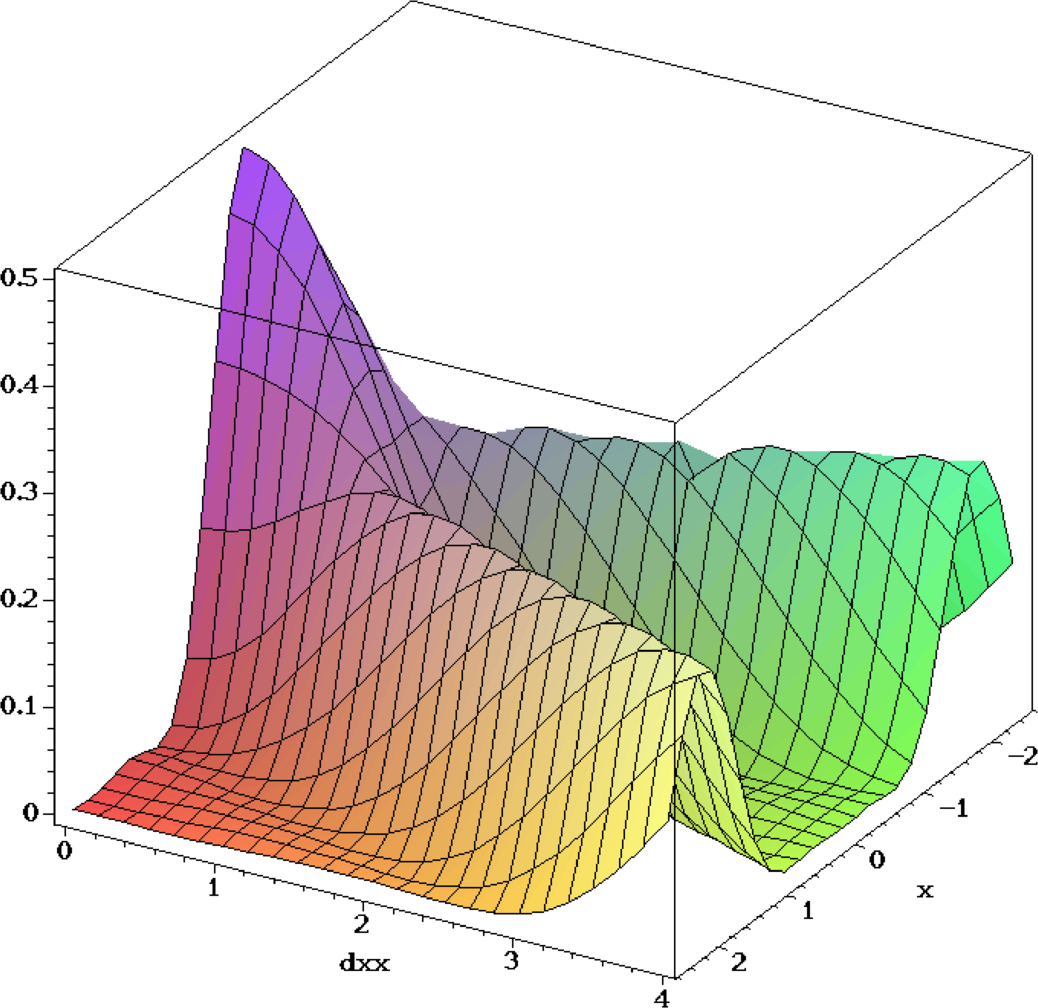

Querschnitt zweier inkohärenter Punktquellen als Funktion des Abstandes (links) und Bild der Intensitätsverteilung bei einem Abstand von 1.
_____________________________________________________________________
Wenn das zu untersuchende Objekt in ein Medium mit dem
Brechungsindex n eingebettet ist, dann verbessert sich die
Auflösung auf sin αK = 1.22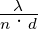 , da in diesem Medium die
Wellenlänge ja λ′ = λ∕n ist.
, da in diesem Medium die
Wellenlänge ja λ′ = λ∕n ist.
 Lizenzinformationen
Lizenzinformationen