__________________________________________________________________________
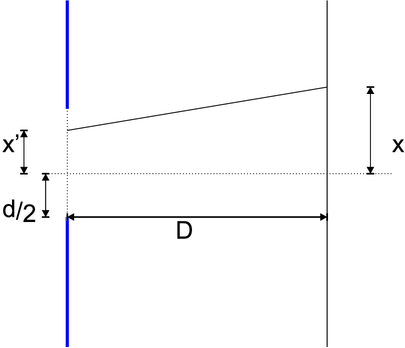
Berechnung der Fresnelbeugung an einer Halbebene.
_____________________________________________________________________

| Literatur | |
Hier wird die Diskussion des Fresnel-Huygensschen Prinzips (siehe Abschnitt 3.4) wieder aufgenommen. Bei der damaligen Betrachtung wurde angenommen, dass sich der Abstand zwischen einem Punkt in der Quellebene und einem Punkt in der Beobachtungsebene kaum ändert (siehe Gleichung (3.4)).
__________________________________________________________________________

Berechnung der Fresnelbeugung an einer Halbebene.
_____________________________________________________________________
Bei der Beugung interferiert Licht von Kugelwellen aus allen Punkten mit den Koordinaten x′ im Beobachtungspunkt mit der Koordinate x. Für eine einzelne Teilwelle ist der Weg
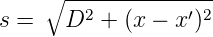 | (3.1) |
Entsprechend ist die komplexe Amplitude am Punkt x gegeben durch
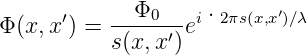 | (3.2) |
Die Amplitude am Punkt x ist dann nach Fresnel-Huygens
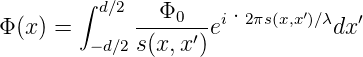 | (3.3) |
da wir Kugelwellen haben. Diese Gleichung kann numerisch gelöst werden. Es existieren die folgenden Näherungen:
Bei beiden Näherungen wird nur das rein imaginäre Argument der der Exponentialfunktion approximiert. Der Faktor 1∕s wird beide Male konstant gesetzt, das heisst, die Amplitudenvariation wegen der unterschidlichen Distanzen wird vernachlässigt.
| Literatur | |
Wir betrachten nur Orte, bei denen |x −x′|«D sind. Dann ist
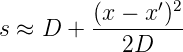 | (3.4) |
und 1∕s ≈ 1∕D. Das heisst auch, dass die Phase ist proportional zu (x −x′)2. Unser Integral wird dann
![Φ0 ∫ d∕2 i·2πs(x,x′)∕λ ′ Φ0 ∫ d∕2 i·2 π[D+ (x′−x)2∕2D]λ ′
Φ(x ) = --- e dx = --- e dx
D −d∕2 D − d∕2](op-2016-2017422x.png) | (3.5) |
und
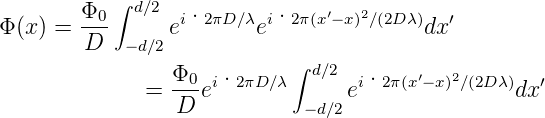 | (3.6) |
Mit der Variablentransformation ξ = x′−x und damit den Grenzen ξu = −d∕2 −x und ξo = d∕2 −x wird das Integral zu
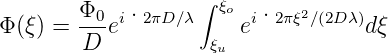 | (3.7) |
Das verbleibende Integral ∫ ξuξoei·2πξ2∕2Dλdξ kann als Summe und Differenz der Fresnelschen Integrale geschrieben werden. Wir verwenden, dass eiα = cos α + i sin α ist.
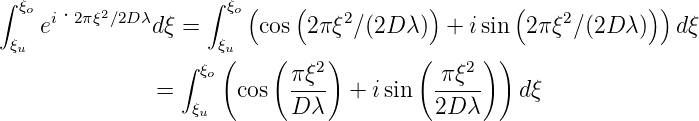 | (3.8) |
Dieses Integral, nach Real- und Imaginärteil aufgetrennt und normiert ergibt die Fresnelschen Integrale
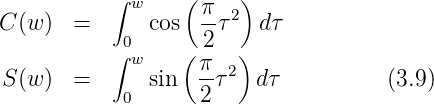
Die Funktion Φ(x) kann als Differenz zweier Fresnelscher Integrale geschrieben werden
![Φ(x ) = K [C ((d∕2 − x)·k ) − C ((− d∕2 − x)·k )]
+i·K [S ((d∕2 − x)·k ) − S ((− d∕2 − x)(·3k.1)]0)](op-2016-2017427x.png)
wobei K eine von der Intensität abhängige Konstante ist.
__________________________________________________________________________
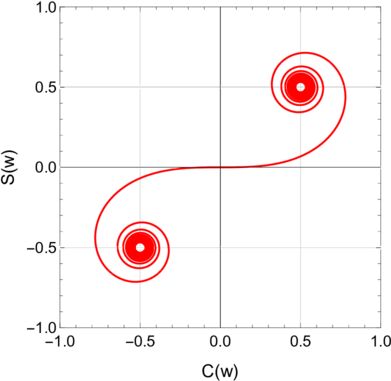
Die Cornu-Spirale. Aufgetragen ist die parametrische Kurve (C(w),S(w)) mit −∞≤w ≤∞. Die linke untere Spirale entspricht w = −∞, die rechte obere Spirale w = ∞.
_____________________________________________________________________
Die durch F(w) = C(w) + iS(w) definierte Ortskurve ist die Cornu-Spirale. Dies e-Funktion beschreibt eine längentreue Abbildung der reellen Achse w auf die komplexe C,S-Ebene. Mit dieser Konstruktion kann auf einfachem graphischem Wege das Beugungsmuster konstruiert werden. Dazu zeichnet man vom Ortspunkt der unteren Integrationsgrenze zum Ortspunkt der oberen Integrationsgrenze eine Linie. Deren Länge gibt die Amplitude, deren Winkel zur reellen Achse die Phase. Damit kann das Fresnel-Beugungsbild eines Spalts berechnet werden.
__________________________________________________________________________
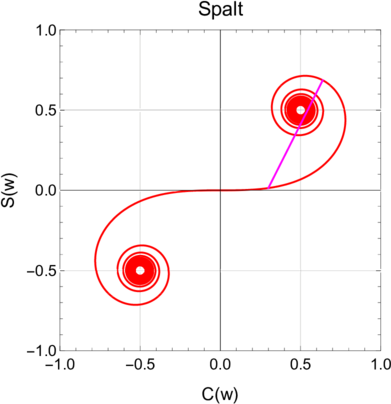
Cornu-Spirale mit einem Spalt der Breite 1.0 = w2 −w1, hier von w1 = 0.3 bis w2 = 1.3.
_____________________________________________________________________
_____________________________________________________________________
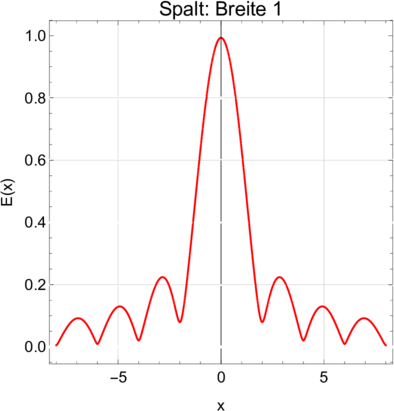
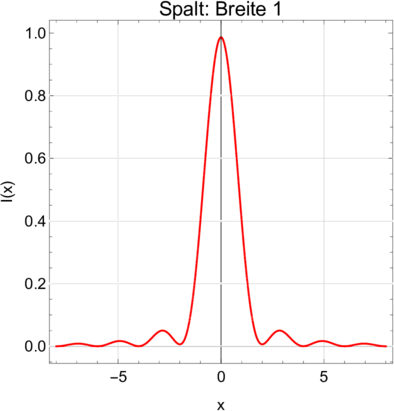
Fresnelsches Beugungsmuster an einem Spalt der Breite 1. Links die Amplitude und rechts die Intensität, die einzige direkt beobachtbare Grösse.
_____________________________________________________________________
Wenn man die untere Integrationsgrenze nach −∞ gehen lässt und bei der oberen Integrationsgrenze d gegen Null gehen lässt, bekommt man das Beugungsbild an einer Kante. Wir tragen nun die Strecke vom Zentrum der linken Spirale (F(−∞) = −1∕2(1 + i)) aus zum Ortspunkt korrespondierend zu x ab. Wir sehen, dass im Schattenbereich (bis der bewegliche Ortspunkt 0, 0 erreicht) die Amplitude monoton zunimmt. Dann beginnt eine Oszillation, die als die Interferenzmuster im hellen Bereich beobachtet werden kann.
Abbildung 3.11.1 zeigt eine ausgewählte Position in der Cornu-Spirale. Ersichtlich ist in der Abbildung und in Abbildung 3.11.1, dass bei einer einfallenden Intensität mit dem Betrage 2 das transmittierte Licht an gewissen Orten eine höhere Intensität hat
__________________________________________________________________________
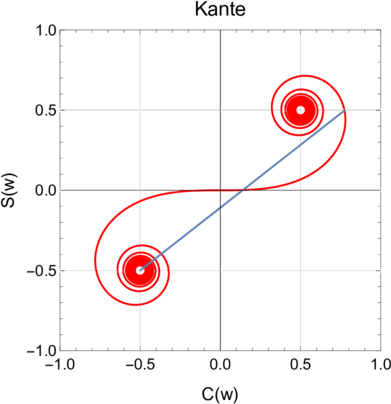
Cornu-Spirale für eine Kante. Die Linie geht von w1 = −∞ nach w2 = 1.06.
_____________________________________________________________________
_____________________________________________________________________
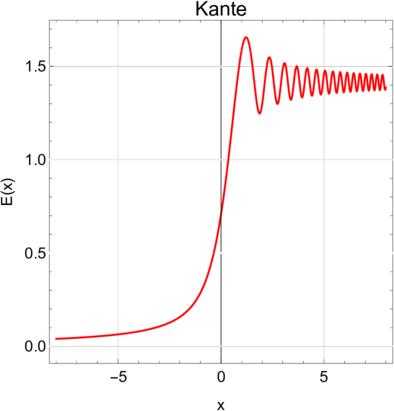
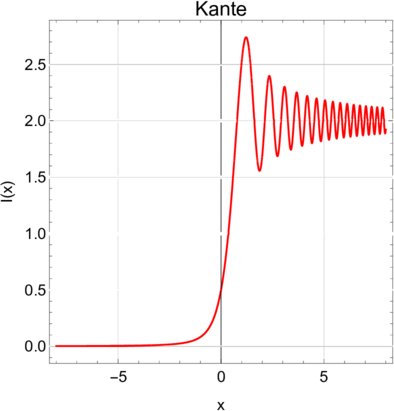
Fresnelsches Beugungsmuster an einer Halbebene. Links die Amplitude und rechts die Intensität, die einzige direkt beobachtbare Grösse.
_____________________________________________________________________
| Literatur | |
Jacques Babinet hat im 19. Jahrhundert beobachtet, dass die Beugungsmuster komplementärer Beugungsobjekte identisch sind. Abbildung 3.11.2 zeigt ein Beispiel komplementärer Beugungsobjekte.
__________________________________________________________________________

Zwei komplementäre Beugungsobjekte zur Illustration von Babinets Prinzip.
_____________________________________________________________________
Anhand der Cornu-Spirale in Abbildung 3.11.1 kann nach Hecht [Hec05, p. 817] das Babinetsche Prinzip verstanden werden.
__________________________________________________________________________
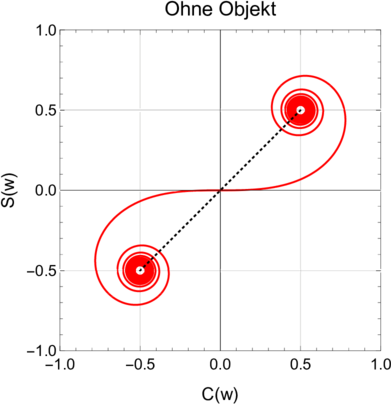
Ohne beugendes Objekt erstreckt sich die Phase in der Cornu-Spirale von −(1 + i)∕2 bis (1 + i)∕2.
_____________________________________________________________________
Abbildung 3.11.2 zeigt die Amplitude und Phase ohne Beugungsobjekt. Bei einem Spalt bekommen wir eine Situation wie in Abbildung 3.11.1.
__________________________________________________________________________
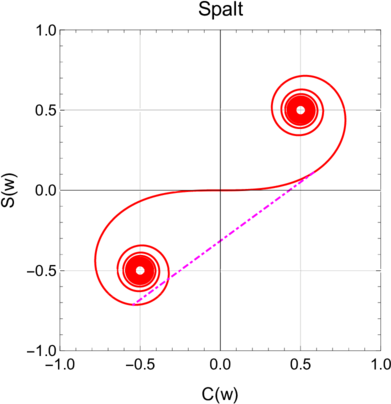
Phase in der Cornu-Spirale für w1 = −1.4 und w2 = 0.6, also w = 2.
_____________________________________________________________________
Abbildung 3.11.2 zeigt die Phase bei einem Spalt. Die Beugung an der linken Kante und an der rechten Kante des komplementären Streifens mit gleicher Breite wie die Spaltbreite kann wie in Abbildung 3.11.1 dargestellt werden.
__________________________________________________________________________
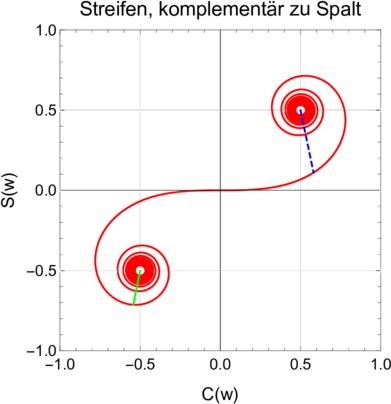
Beugung an den beiden Kanten einer Linie mit der Breite w = 2 und den Werten w = −1.4 (links) und w = 0.6 (rechts).
_____________________________________________________________________
Die einzelnen Linien in den Abbildungen 3.11.2 bis 3.11.2 stellen Amplitude und Phase des elektrischen Feldes dar. Das Babinetsche Prinzip besagt nun, dass die elektrischen Felder nach der Beugung an einem Spalt summiert mit den elektrischen Feldern nach der Beugung an einem Streifen das elektrische Feld ohne Beugungsobjekt geben müssen.
__________________________________________________________________________
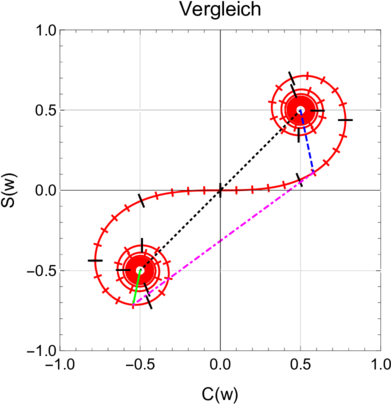
Illustration des Babinetschen Prinzips anhand der Beugung an einem Spalt (Abb. 3.11.2) addiert zur Beugung an einem Streifen (Abb. 3.11.2). Diskussion nach Hecht [Hec05, p. 817].
_____________________________________________________________________
In der Abbildung 3.11.2 (nach Hecht [Hec05, p. 817]) wird
gezeigt, dass der 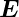 -Feldvektor der ungestörten Lichtwelle
(schwarz) die Summe aus den
-Feldvektor der ungestörten Lichtwelle
(schwarz) die Summe aus den 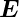 -Feldern der Beugung am
Spalt (magenta) und der Beugung an den zwei Kanten des
Streifens (grün und blau) ist.
-Feldern der Beugung am
Spalt (magenta) und der Beugung an den zwei Kanten des
Streifens (grün und blau) ist.
Die Gleichung (3.4) kann weiter vereinfacht werden, wenn
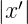 ⋘
⋘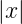 ist. Dann bekommen wir
ist. Dann bekommen wir
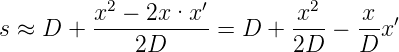 | (3.11) |
und 1∕s ≈ 1∕D. Nun ist die optische Distanz s eine lineare Funktion von x′. Die Approximation gilt nur, wenn das Beugungsobjekt klein gegen die Distanz zu Objekt und der Grösse des Beugungsmusters ist. Diese Fernfeld-Approximation nennt man die Fraunhofer-Näherung.
Das heisst, dass die Phase proportional zu C + x′ ist. Unser Integral wird dann
![Φ0 ∫ d∕2 i·2πs(x,x′)∕λ ′ Φ0 ∫ d∕2 i·2 π[D+ x2−-xx′]λ ′
Φ(x ) = --- e dx = --- e 2D D dx
D −d∕2 D − d∕2](op-2016-2017433x.png) | (3.12) |
und
![∫ d∕2 [ x2]
Φ(x ) = Φ0- ei·2π D+ 2D ∕λe−i·2πxx′∕(2Dλ)dx′
D −d∕2 [ ]
Φ i· (2π∕λ) D+-x2 ∫ d∕2 [ πx ]
= -0-e 2D exp − i·----x′ dx ′
D −d∕2 D λ](op-2016-2017434x.png) | (3.13) |
Würde das Integral von −∞ nach +∞ laufen, hätten wir eine Fouriertransformation.
Um aus Gleichung (3.13) ein Integral über ℝ zu machen, brauchen wir eine Fensterfunktion. Die Heaviside-Θ-Funktion erlaubt dies. Sie berechnet sich aus der Delta-Funktion über
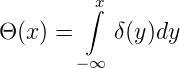 | (3.14) |
Die Fensterfunktion oder Spaltfunktion gS(x) kann dann aus der Subtraktion zweier verschobener Θ-Funktionen erzeugt werden:
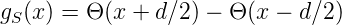 | (3.15) |
Gleichung (3.13) wird mit Gleichung (3.15) umgeschrieben:
Damit ist klar, dass die Fraunhofer-Näherung für das Amplituden-Beugungsmuster eines Spaltes die inverse Fouriertransformation (Rücktransformation) der Spaltfunktion multipliziert mit einem Phasenfaktor ist. Die inverse Fouriertransformation der Spaltfunktion ist
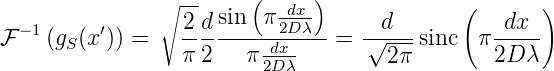 | (3.17) |
Dabei ist sinc(x) = 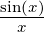 eine übliche Kurzschreibweise.
eine übliche Kurzschreibweise.
Die Amplitude Φ hier ist zum Beispiel das elektrische Feld E. Dann ist die beobachtbare Intensität wie im Abschnitt 2.3 gegeben.
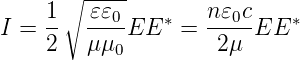 | (3.18) |
Wir bekommen also für das Beugungsmuster der Intensität beim Einzelspalte in der Fraunhofer-Näherung
| Literatur | |
Die bis jetzt besprochenen Beugungseffekte haben die folgenden Eigenschaften:
Ist eine der obigen Bedingungen nicht erfüllt, spricht man von Fresnelscher Beugung. Eine andere Formulierung der Bedingungen der Fraunhoferschen Beugung ist
|
________________________________________________________________
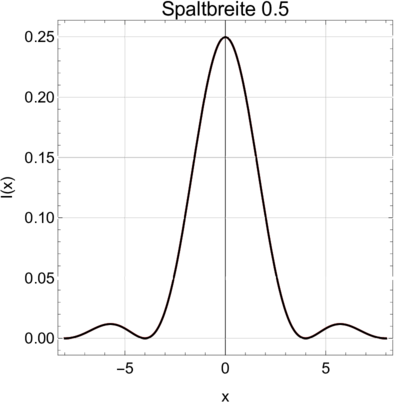
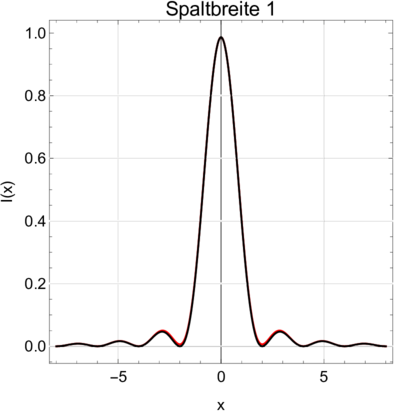
Vergleich der Fresnelbeugung (rot) mit der Fraunhoferbeugung (schwarz) für Spaltweiten von 0.5 und 1.
_____________________________________________________________________
_____________________________________________________________________
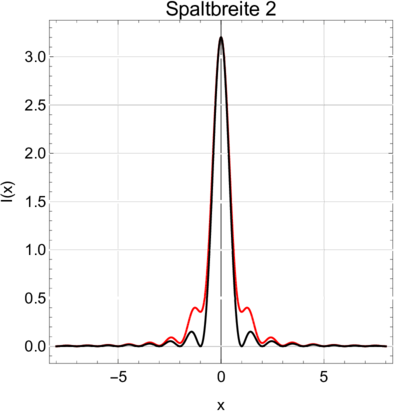
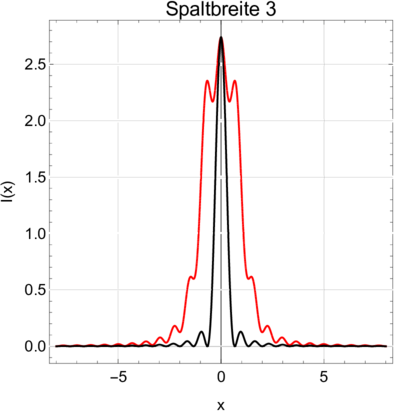
Vergleich der Fresnelbeugung (rot) mit der Fraunhoferbeugung (schwarz) für Spaltweiten von 2 und 3.
_____________________________________________________________________
_____________________________________________________________________
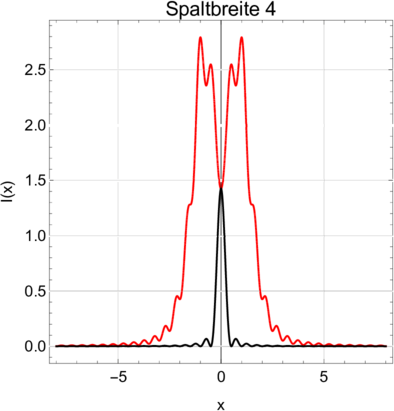
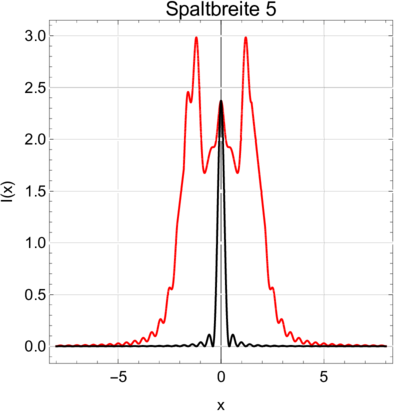
Vergleich der Fresnelbeugung (rot) mit der Fraunhoferbeugung (schwarz) für Spaltweiten von 4 und 5.
_____________________________________________________________________
_____________________________________________________________________
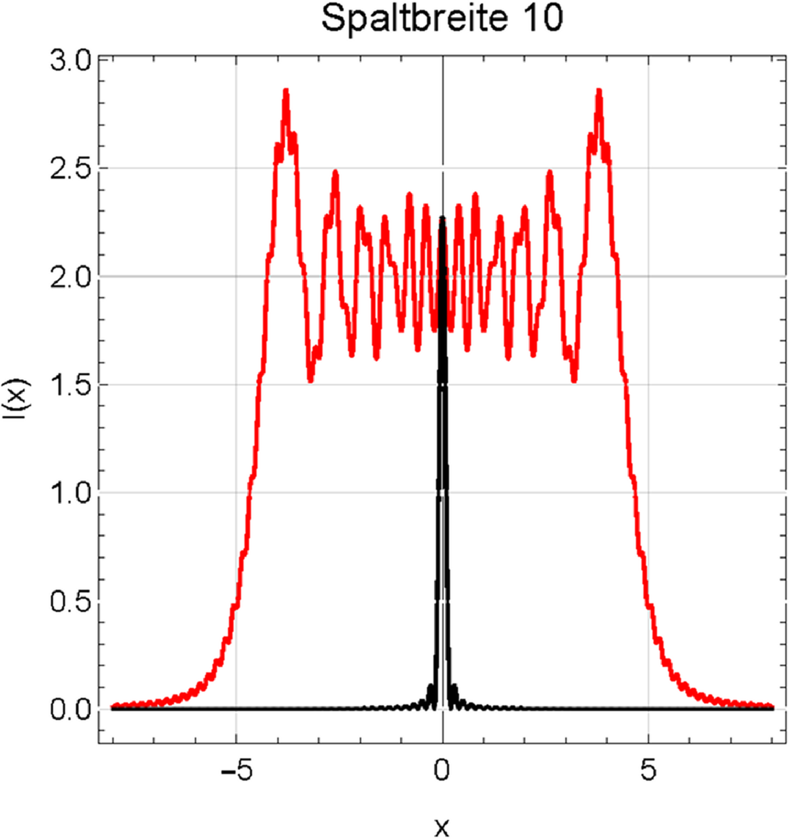
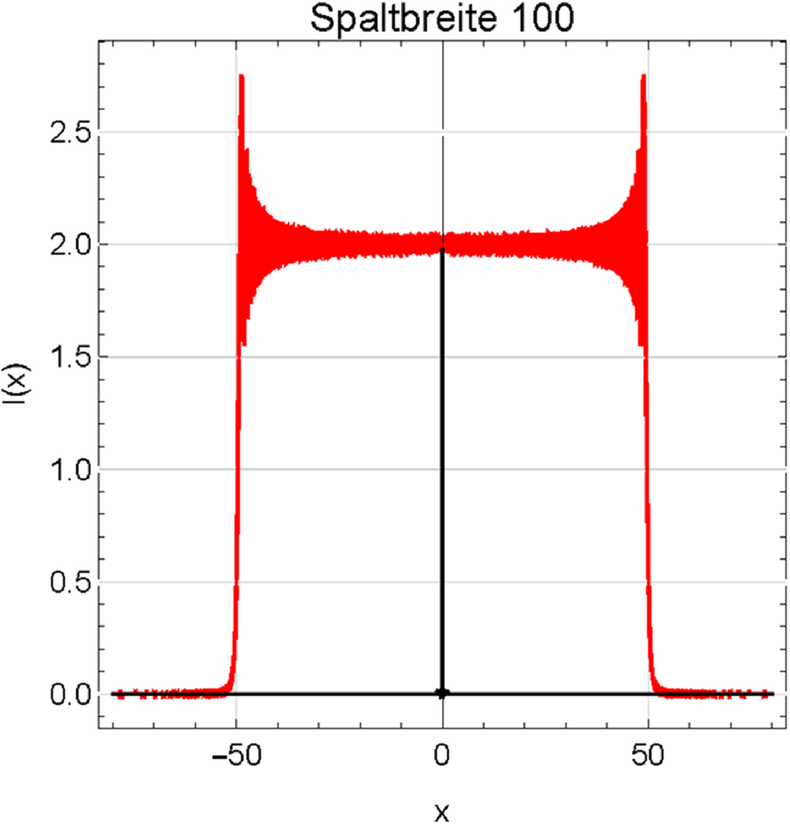
Vergleich der Fresnelbeugung (rot) mit der Fraunhoferbeugung (schwarz) für Spaltweiten von 10 und 100. Beachten Sie die geänderte x-Achse bei der Spaltbreite 100.
_____________________________________________________________________
Sehr schön ist aus den Abbildungen zu ersehen, dass sich die transmittierte Intensität bei sehr breiten Spalten wie aus der geometrischen Optik erwartet verhält. Das Überschwingen an den Kanten in Abbildung 3.11.4 ist auch von Fouriertransformationen bekannt. Es heisst Gibbs-Phänomen und entsteht immer, wenn bei Integraltransformationen (Fourier oder eben die Wellentheorie der Beugung) die Bedingung der beliebig oft stetigen Differenzierbarkeit verletzt ist.
| Literatur | |
Wenn die Polarisation der Lichtwelle nicht relevant ist, kann die vektorielle Wellengleichung, wie sie aus den Maxwellgleichungen abgeleitet wird, als skalare Wellengleichung geschrieben werden. Beim Fresnel-Huygenschen Prinzip wir die anregende Welle in eine unendliche Anzahl von Punktstörungen aufgeteilt. Diese punktförmigen Anregungen beinhalten nun alle räumlichen Frequenzen.
Der alternative Ansatz von Kirchhoff analysiert die in der Anregung und dem Beugungshindernis vorhandenen Frequenzen und berechnet so das Beugungsmuster über eine Fourieranalyse.
Kirchhoff betrachtet skalare monochromatische Wellen [Hec05, p. 820], [AW95]. Diese haben die Form
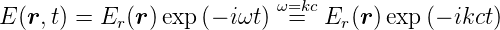 | (3.20) |
und sind die Lösung der skalaren Form der vektoriellen Wellengleichung (2.1). Wird Gleichung (3.20) eingesetzt, ergibt sich die rein räumliche partielle Differentialgleichung
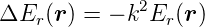 | (3.21) |
Gleichung (3.21) wird in der Literatur Helmholtz-Gleichung genannt. Nach Hecht [Hec05, pp. 1041-1042] kann die Gleichung mit dem zweiten Greenschen Satz gelöst werden. Nach [AW95, pp. 58-60] beruht dies auf dem Gaussschen Satz
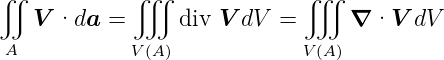 | (3.22) |
mit einer geschlossenen Oberfläche A. Weiter werden die Identitäten für Vektorableitungen
Die Differenz der beiden Gleichungen eliminiert das Skalarprodukt der Gradienten
oder in Integralform
Nach Hecht [Hec05, p. 1041] nimmt man nun an, dass u und v die Helmholtzgleichung (3.21) lösen, dass also Δu = −k2u und Δv = −k2v ist. Dann ist die linke Seite von Gleichung (3.25) null, also haben wir
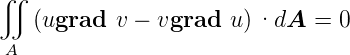 | (3.26) |
__________________________________________________________________________
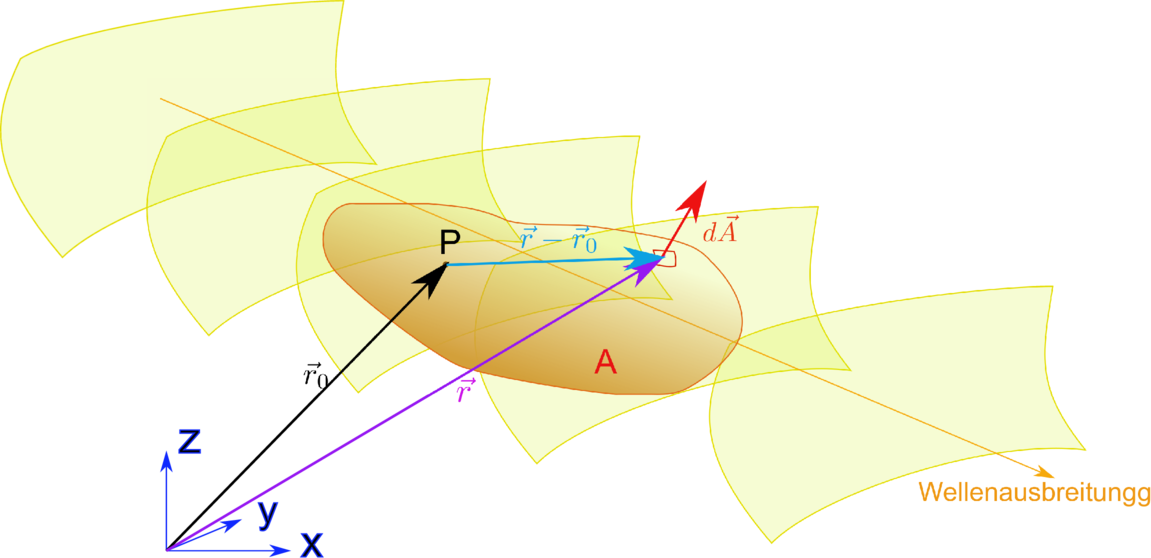
Geometrie zur Herleitung des Kirchhoffschen Integralsatzes (Adaptiert aus [Hec05, pp. 819 ff]).
_____________________________________________________________________
Danach wird u = Er( ) gesetzt und v als Kugelwelle um
den Nullpunkt
) gesetzt und v als Kugelwelle um
den Nullpunkt
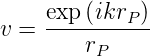 | (3.27) |
Dabei ist 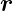 p =
p = 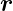 −
−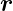 0 der Vektor eines Beobachtungspunktes
vom Punkt P und rP der dazugehörige Abstand. P
soll innerhalb der geschlossenen Fläche A liegen. In
Kugelkoordinaten ist
0 der Vektor eines Beobachtungspunktes
vom Punkt P und rP der dazugehörige Abstand. P
soll innerhalb der geschlossenen Fläche A liegen. In
Kugelkoordinaten ist
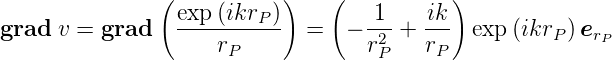 | (3.28) |
 rP zeigt von P weg nach aussen. Wir subtrahieren also
eine kleine Kugelfläche A mit dem Kugelmittelpunkt bei P
von A und schliessen so die Divergenz aus. Dann lassen
wir A → 0 gehen. Auf der Kugeloberfläche A lautet der
Gradient
rP zeigt von P weg nach aussen. Wir subtrahieren also
eine kleine Kugelfläche A mit dem Kugelmittelpunkt bei P
von A und schliessen so die Divergenz aus. Dann lassen
wir A → 0 gehen. Auf der Kugeloberfläche A lautet der
Gradient
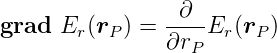 | (3.29) |
Damit wird der Integrand von Gleichung (3.26) innerhalb der kleinen Kugel A
Dieser Integrand soll über eine Kugelfläche A mit dem
Radius rP integriert werden. Alle Vektoren sind weiter radial,
so dass für eine beliebige, gutartige Funktion 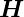 sie Beziehung
sie Beziehung
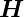 ·d
·d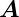 = HrP 2dΩ geschrieben werden kann, wobei dΩ ein
Raumwinkelelement ist. Im Grenzfall A → 0 oder rP → 0
nimmt Er(
= HrP 2dΩ geschrieben werden kann, wobei dΩ ein
Raumwinkelelement ist. Im Grenzfall A → 0 oder rP → 0
nimmt Er(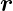 P ) einen konstanten Wert an, nämlich den Wert
Er,P am Ort des Punktes P. Weiter geht exp
P ) einen konstanten Wert an, nämlich den Wert
Er,P am Ort des Punktes P. Weiter geht exp 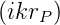 in diesem Falle gegen 1. Die Terme mit rP gehen nach
Null.
in diesem Falle gegen 1. Die Terme mit rP gehen nach
Null.
Wir haben also
Mit 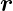 P =
P = 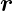 −
−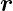 0 kann der Kirchhoffsche Integralsatz so
geschrieben werden:
0 kann der Kirchhoffsche Integralsatz so
geschrieben werden:
Der Kirchhoffsche Integralsatz besagt, dass die skalare Amplitude des elektrischen Feldes aus dem Feld auf einer Integrationsfläche berechnet werden kann.
__________________________________________________________________________
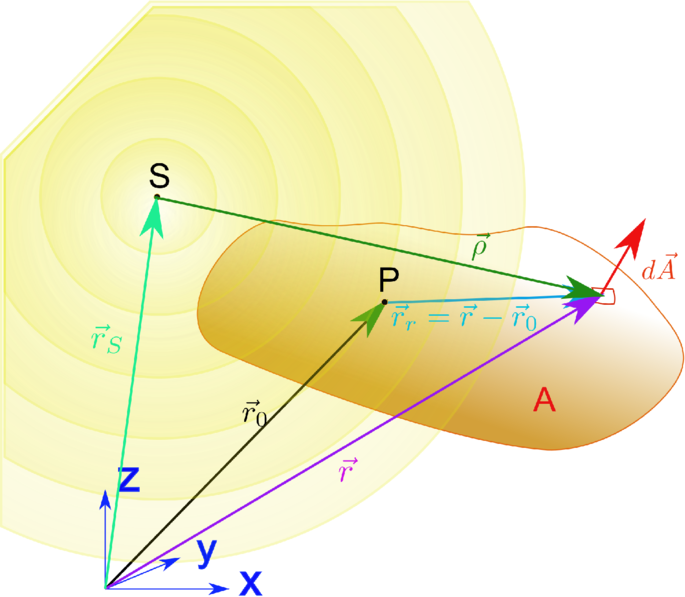
Sizze der Geometrie der Kirchhoff-Theorie (Adaptiert aus [Hec05, pp. 819 ff]).
_____________________________________________________________________
Im Weitern betrachtet man jetzt nach Hecht [Hec05, p. 820]
eine ungestörte Kugelwelle, die von einem Punkt S mit dem
Ortsvektor 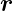 S ausgeht. Dann wird
S ausgeht. Dann wird 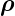 =
= 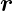 −
−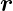 S gesetzt die
Funktion Er(
S gesetzt die
Funktion Er(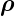 ,t) = Er(ρ,t)
,t) = Er(ρ,t)
![[ ]
E (ρ,t) = E^ (ρ)exp (− iωt) = E exp-(ikρ) exp(− iωt)
r r 0 ρ](op-2016-2017474x.png) | (3.34) |
angesetzt. Weiter setzen wir
Wenn nun wie in der makroskopischen Optik λ «ρ = 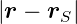 und λ «rp =
und λ «rp = 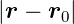 ist, wenn also die Ausdehnungen der
Objekte gross gegen die Wellenlänge sind, können die
quadratischen Terme vernachlässigt werden und Gleichung
(3.33) lautet dann mit k = 2π∕λ dann:
ist, wenn also die Ausdehnungen der
Objekte gross gegen die Wellenlänge sind, können die
quadratischen Terme vernachlässigt werden und Gleichung
(3.33) lautet dann mit k = 2π∕λ dann:
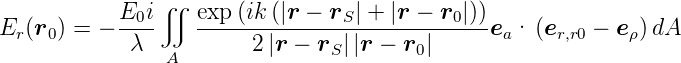 | (3.36) |
Gleichung (3.36) gilt nicht für die Nanooptik, die Wechselwirkung zwischen Nanoteilchen und auch nicht für Mikrowellen.
Hecht [Hec05, p. 824] schliesst aus Gleichung (3.36), dass das Fresnel-Huygenssche Prinzip direkt aus der skalaren Wellengleichung hergeleitet werden kann. Er gibt an, dass bei dieser Herleitung aus der Wellengleichung ein zusätzlicher Phasenfaktor π∕2 entsteht, der in der normalen Ableitung fehlt. Dieser Phasenfaktor ist dann wichtig, wenn die gebeugte Welle mit einer Referenzwelle interferieren soll.
 Lizenzinformationen
Lizenzinformationen