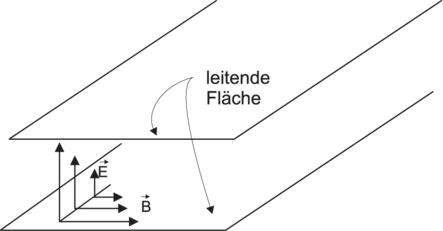
| Abbildung 4.138.: | Schematische Darstellung einer plattengeführten elektromagnetischen Welle. |

Ebene Wellen (Siehe im Anhang Abschnitt A.4) können zwischen zwei Metallplatten problemlos geführt werden. Abb. 4.138 zeigt, dass, wenn das elektrische Feld senkrecht zu den Platten steht, dies mit den Randbedingungen vereinbar ist. Der Abstand der Platten kann so klein man will gewählt werden, Leitung hat man immer noch. Die in der Abbildung gezeigte Welle heisst TEM-Plattenwelle.
| TEM
Wellentyp | Koaxialleitung | Streifenleitung |
|
| Leiter-Grundform |  | 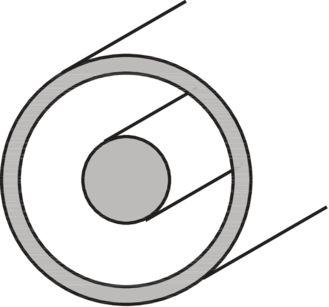 | 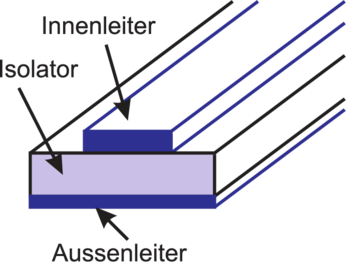 |
| elektrische
und
magnetische
Feldlinien | 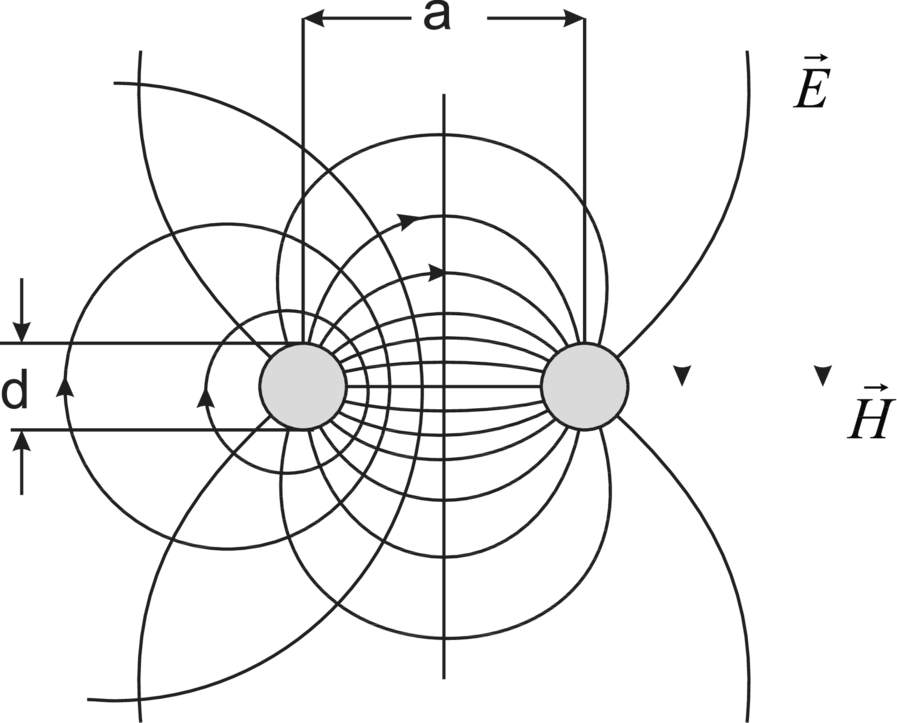 | 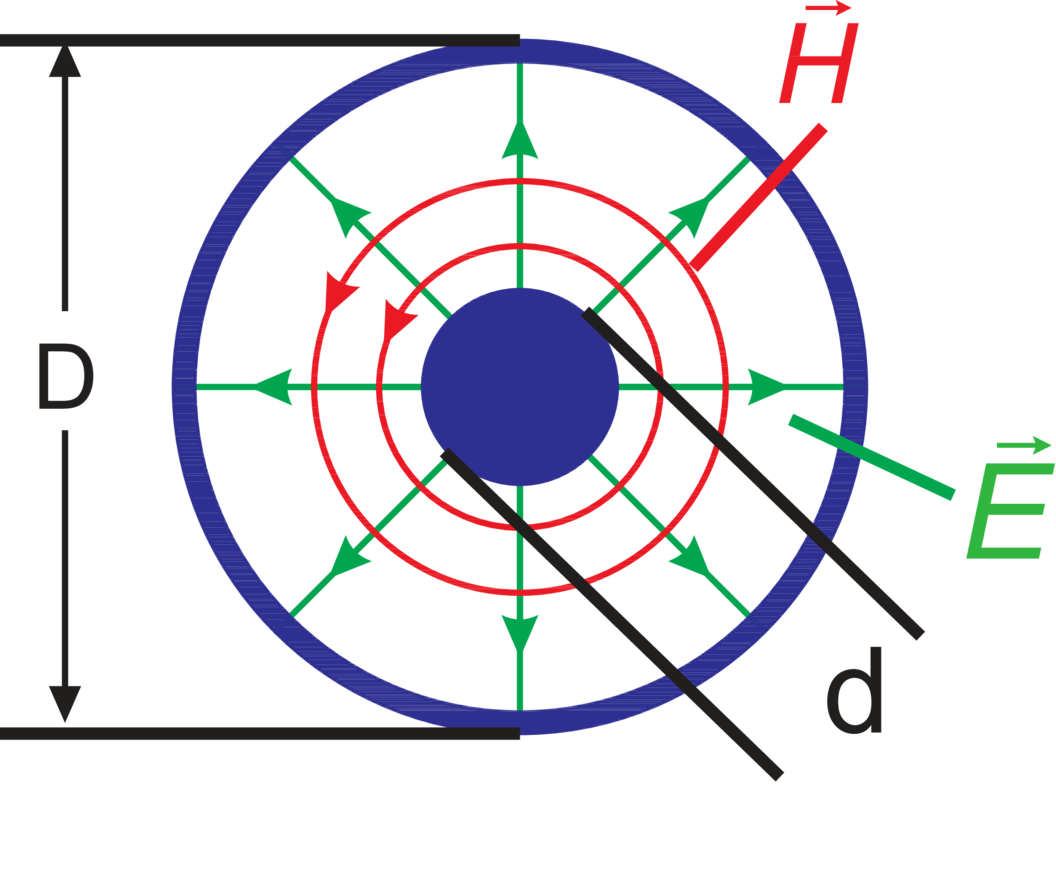 | 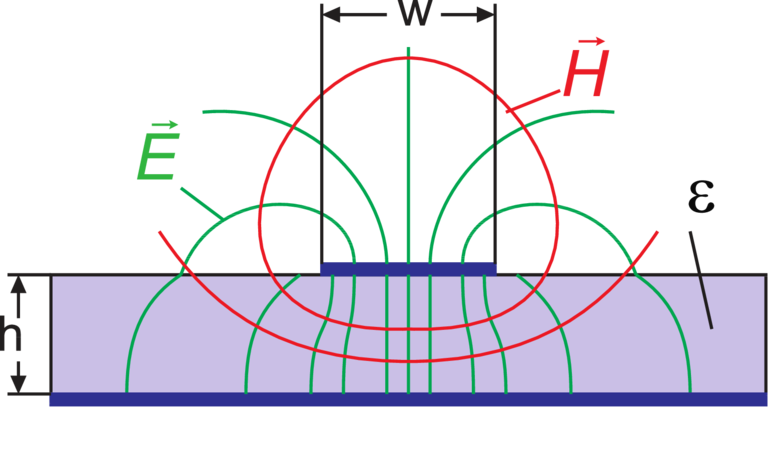 |
| Leitungs-Wellenwiderstand | Z = 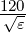 · ln · ln 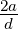 [Ω]
für a > 2.5·d [Ω]
für a > 2.5·d | Z =
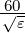 · ln · ln 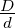 [Ω] [Ω] | Z = 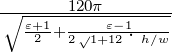 · ·
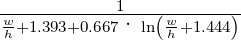 [Ω] für w ≥h
[Ω] für w ≥h |
| Variationen
in den
Ausführungsformen |  Anwendung als Antennenleitung bei hohen Frequenzen (Z = 240Ω,Z = 300Ω) | Der Aussenleiter
wird meist
als Drahtgeflecht
ausgeführt.
(Z = 50Ω,Z =
60Ω,Z =
75Ω,Z = 200Ω) | 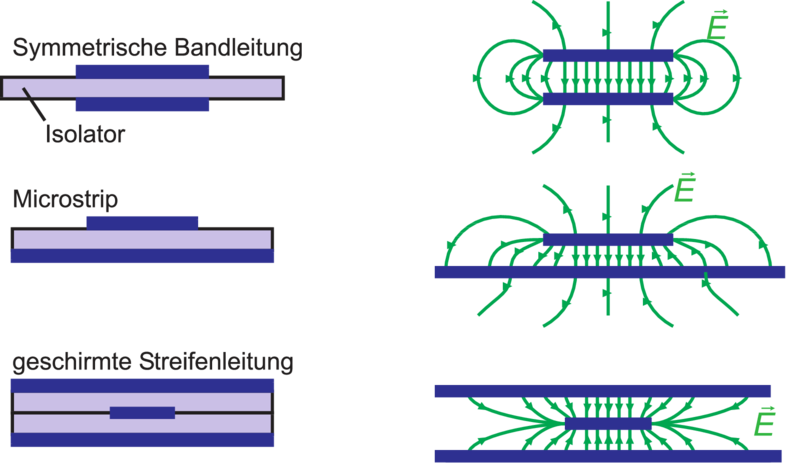 |
| Tabelle 4.7.: | Homogene Leitungen, deren Abmessungen klein gegen die Wellenlänge sind |
Tabelle 4.7 zeigt eine Zusammenstellung verschiedener Wellenleiter, bei denen die Dimensionen klein gegen die Wellenlänge sind.
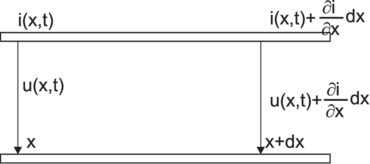
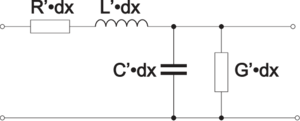
| Abbildung 4.139.: | Links die Darstellung eines Wellenleiters. Spannung und Strom ändern sich bei einer Verschiebung um dx um die entsprechenden infinitesimalen Grösse. Rechts das Ersatzschaltbild. |
Nach Abb. 4.139 kann man Zweidrahtleitungen, Koaxialleitungen und Streifenleitungen mit folgendem phänomenologischen Ansatz[Wei95] behandeln: Die Änderung der Spannung u(x,t) und des Stromes i(x,t) längs der Leiterstrecke dx geschieht wegen
Dies ist das in Abb. 4.139, rechts, angegebene Ersatzschaltbild. Für die Strom-und Spannungsänderung erhalten wir
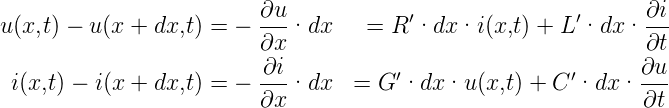
Die Leitungsgleichungen in differentieller Form lauten also
Wenn Gleichung (4.1) nach x und Gleichung (4.2) nach t abgeleitet werden, können die Gleichungen kombiniert werden zur Leitungs-Wellengleichung10 oder Telegraphengleichung.
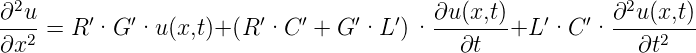 | (4.3) |
oder für den Strom
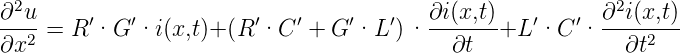 |
Lösungen der Leitungs-Wellengleichung bekommt man mit dem Ansatz u(x,t) = u(ω)·e−γx·eiωt + c.c. sowie i(x,t) = i(ω)·e−γx·ejωt + c.c.
Damit wird die Fortpflanzungskonstante
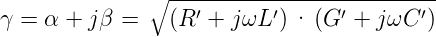 | (4.4) |
Setzt man den Ansatz in Gleichungen (4.1) und (4.2) ein, so sind die komplexen Amplituden
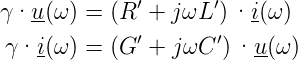
Der Quotient aus komplexer Spannungsamplitude und Stromamplitude ist der Leitungs-Wellenwiderstand
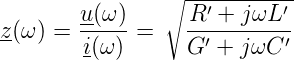 | (4.5) |
Bei einer verlustlosen Leitung (R′ = 0, G′ = 0) ist
γ = α + jβ = jω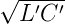 , also rein imaginär. Die Dämpfung ist
null (α = 0) und β ≡ ω∕cph = ω
, also rein imaginär. Die Dämpfung ist
null (α = 0) und β ≡ ω∕cph = ω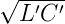 . Damit ist der
Wellenwiderstand der verlustlosen Leitung
. Damit ist der
Wellenwiderstand der verlustlosen Leitung
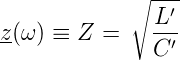 | (4.6) |
und die Phasengeschwindigkeit der Leitungswelle
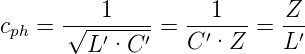 | (4.7) |
Als allgemeine Lösung setzen wir eine hin- und eine herlaufende Welle an.
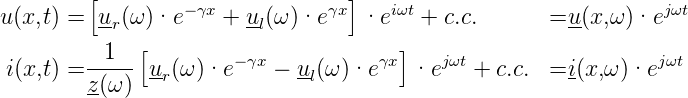
Man erhält diese Gleichungen, indem Gleichung (4.5) benutzt wird. Eine nach links laufende Welle kehrt dabei die Stromrichtung um.
Unter Verwendung der Koordinaten in Abb. 4.140 bekommt man für x2
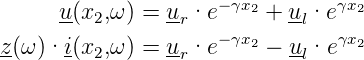
Wir können diese Gleichungen nach ur und ul auflösen und erhalten
Eingesetzt in unseren Ansatz ergibt sich
Diese Gleichung kann auch in Matrixschreibweise angegeben werden
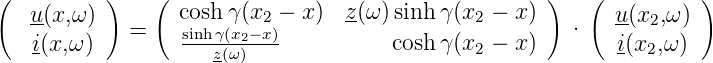 | (4.12) |
Damit stehen die Leitungsgleichungen in Vierpol-Kettenform da (siehe auch Abb. 4.140, rechts).
Mit den Leitungsgleichungen können
Im zweiten Fall wendet man die Gleichung (4.12) an und erhält für die Anordnung nach Abb. 4.141
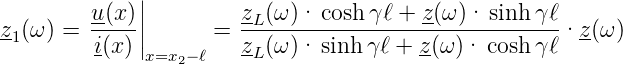 | (4.13) |
Für ein verlustloses Leitungsstück gilt die Gleichung (4.6), z(ω) ≡Z und die dazu führenden Überlegungen so dass die Gleichungen (4.10) und (4.11)
wird. Analog ergibt sich für die Widerstandstransformation nach Gleichung (4.13)
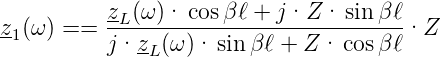 | (4.16) |
Bei einer kurzgeschlossenen, verlustlosen Leitung (dann ist zL(ω) = 0) ist die Eingangsimpedanz mit Gleichung (4.16) durch
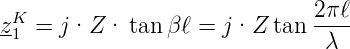 | (4.17) |
gegeben. Die Schaltung und der Eingangswiderstand sind in Abb. 4.142 angegeben. Die Eingangsimpedanz wird zweckmässigerweise als Funktion von ℓ∕λ angegeben. Man findet folgendes Verhalten:
Dann wiederholt sich dieses Verhalten.
In Abb. 4.143 links ist gezeigt, dass man mit einer einzelnen Stichleitung eine konzentrierte Impedanz z1K erzeugen kann. Auf der rechten Seite in dieser Abbildung sieht man, dass eine ℓ = λ∕4-Leitung als verlustfreie Stütze für eine Lecherleitung dienen kann.
Wenn eine Leitung der Impedanz Z an einen Verbraucher der Impedanz zL angeschlossen werden muss, dann kann man diese Anpassung erreichen, indem man wie in Abb. 4.144 eine Leitung variabler Länge und eine Stichleitung mit verschiebbarem Kurzschluss verwendet. Eine vollständige Anpassung an den komplexen Verbraucher zL ist mit drei Stichleitungen im Abstand λ∕4 möglich. Dabei muss, anders als in Abb. 4.144 der Abstand zum Verbraucher nicht geändert werden. Die Berechnung erfolgt, indem man die obigen Formeln abschnittsweise anwendet. Alternativ kann man mit einem Smith-Diagram die Aufgabe graphisch lösen.
Bei einer offenen, verlustlosen Leitung (dann ist zL(ω) = ∞) ist die Eingangsimpedanz mit Gleichung (4.16) durch
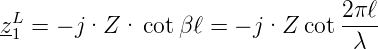 | (4.18) |
gegeben. Die Schaltung und der Eingangswiderstand sind in Abb. 4.145 angegeben. Die Eingangsimpedanz wird zweckmässigerweise als Funktion von ℓ∕λ angegeben. man findet folgendes Verhalten:
Dann wiederholt sich dieses Verhalten.
Wie Abb. 4.146 zeigt, kann man eine vollständige Anpassung einer Leitung mit der Impedanz Za an eine Leitung der Impedanz Zb erreichen, wenn man, nach Gleichung (4.16) ein Zwischenstück der Länge λ∕4 mit dem Wellenwiderstand
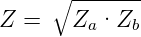 | (4.19) |
einfügt. Ein analoges Beispiel ist die Vergütung von Linsen.
Zur Entspiegelung bringt man, wie in Abb. 4.146, Mitte,
gezeigt eine Schicht der Dicke λ∕4 mit dem Brechungsindex
n = 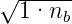 =
= 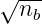 . Dies ist äquivalent zur Gleichung (4.18),
da für ebene elektromagnetische Wellen gilt:
. Dies ist äquivalent zur Gleichung (4.18),
da für ebene elektromagnetische Wellen gilt:
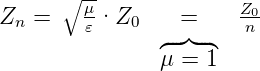 | (4.20) |
Weiter kann man aus den obigen Gleichungen ableiten, dass bei hohen Frequenzen 50 Ω-Messkabel stets mit der Nennimpedanz abgeschlossen werden müssen. Wenn zum Beispiel ein 1-Meter-Kabel mit der Dielektrizitätszahl 𝜀 = 1 mit einem hochomigen Anschluss (z.B. ein Oszilloskop) verbunden wird, dann liegt am Eingang der Leitung bei etwa 53 MHz ein Kurzschluss vor.
Aus den Maxwellgleichungen (siehe Anhang A.1) sowie den Materialgleichungen für isotrope Materialien

erhält man die skalaren Gleichungen
Unter der Annahme, dass sich die Wellen in die
x-Richtung ausbreiten (Siehe Abb. 4.147), dass eine
TEM-Welle und dass eine homogene Leitung vorliegt
(d.h. 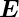
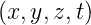 =
= 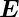
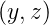 e−γx+jωt + c.c. sowie
e−γx+jωt + c.c. sowie
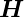
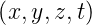 =
= 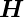
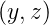 e−γx+jωt + c.c. mit γ = α + jβ der
Fortpflanzungskonstanten, wobei α die Dämpfungskonstante
und β der Wellenvektor ist) reduzieren sich die Gleichungen
auf
e−γx+jωt + c.c. mit γ = α + jβ der
Fortpflanzungskonstanten, wobei α die Dämpfungskonstante
und β der Wellenvektor ist) reduzieren sich die Gleichungen
auf
Die Fortpflanzungskonstante γ erhalten wir durch die Kombination der Gleichungen (4.30), (4.31), (4.33) und (4.34).
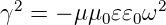 | (4.37) |
oder
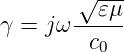 | (4.38) |
wobei c0 die Vakuumlichtgeschwindigkeit ist.
Weiter wird
Also ist das Amplitudenverhältnis an einem beliebigen Ort.
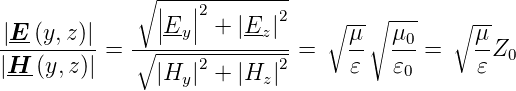 | (4.41) |
mit Z0 = 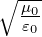 = 120π
= 120π![[Ω ]](phys_elektr1022x.png) ≈ 377Ω der Wellenwiderstand des
Vakuums. Also ist in einer TEM-Welle das Amplitudenverhältnis
zwischen elektrischem und magnetischem Feld überall gleich
dem einer ebenen Welle!
≈ 377Ω der Wellenwiderstand des
Vakuums. Also ist in einer TEM-Welle das Amplitudenverhältnis
zwischen elektrischem und magnetischem Feld überall gleich
dem einer ebenen Welle!
Das 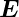 -Feld ist rotationsfrei in der yz-Ebene, da die
x-Komponente
-Feld ist rotationsfrei in der yz-Ebene, da die
x-Komponente
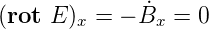
und da auch Hx = 0 ist.
Damit kann man das 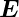 -Feld mit einem elektrostatischen
Potential φ darstellen, also
-Feld mit einem elektrostatischen
Potential φ darstellen, also
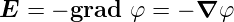 | (4.42) |
Zusammen mit div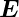 =
=  ·
·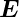 = 0 bekommt man die
Potentialgleichung
= 0 bekommt man die
Potentialgleichung
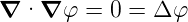 | (4.43) |
Also ist das 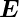 -Feld bei TEM-Wellen einem statischen
-Feld bei TEM-Wellen einem statischen
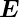 -Feld, beschrieben durch die Elektrostatik und die
Potentialtheorie, äquivalent (Siehe auch Abb. 4.148)
.
-Feld, beschrieben durch die Elektrostatik und die
Potentialtheorie, äquivalent (Siehe auch Abb. 4.148)
.
Das 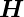 -Feld steht überall senkrecht zum
-Feld steht überall senkrecht zum 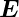 -Feld,
da
-Feld,
da
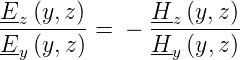 | (4.44) |
Jeder der beiden Koeffizienten kann mit tan α dargestellt
werden. Da die 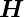 -Feldlinien stets senkrecht zu den
-Feldlinien stets senkrecht zu den
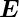 -Feldlinien stehen, verlaufen sie entlang der Potentiallinien
des elektrostatischen Potentials.
-Feldlinien stehen, verlaufen sie entlang der Potentiallinien
des elektrostatischen Potentials.
Wir gehen nun zu integralen Grössen über (Die Integrationswege sind in 4.149 gezeigt). Es liegt, da aus Ex = 0 auch Ḋx = 0 folgt, ein reiner Leitungsstrom vor.
An der Stelle x ist er
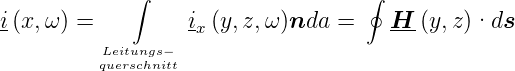 | (4.45) |
Für die Spannung folgt
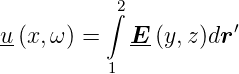 | (4.46) |
Das Vierpol-Ersatzschaltbild eines verlustfreien Leiterstückes wird durch einen Kapazitätsbelag C′ und einen Induktivitätsbelag L′ charakterisiert. Der Wellenwiderstand ist dann
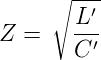 | (4.47) |
und die Phasengeschwindigkeit
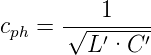 | (4.48) |
Zur Berechnung des Kapazitätsbelages (siehe Abb. 4.150, links) ermitteln wir auf einem Leiterstück der Länge dx die Ladung Q = Q′dx. Aus den Maxwellschen Gleichungen in Integralform
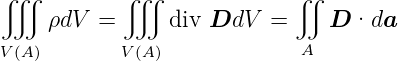
Das erste Integral ergibt (siehe Abb. 4.150, links)
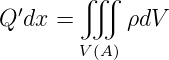
Das Oberflächenintegral über A kann in drei Teile aufgeteilt
werden. Die zwei Zylinderendflächen tragen nichts zum
Integral bei, da dort 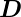 tangential zur Oberfläche ist. Allein
die Zylindermantelfläche trägt zum Integral bei. Das in
Abb. 4.150, links, eingezeichnete Flächenelement hat die
Seiten
tangential zur Oberfläche ist. Allein
die Zylindermantelfläche trägt zum Integral bei. Das in
Abb. 4.150, links, eingezeichnete Flächenelement hat die
Seiten 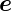 xdx und d
xdx und d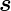 , wobei d
, wobei d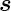 das Linienelement entlang
des Zylinderumfangs ist. Die Richtung von d
das Linienelement entlang
des Zylinderumfangs ist. Die Richtung von d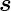 folgt mit
der rechten-Hand-Regel aus der Richtung von
folgt mit
der rechten-Hand-Regel aus der Richtung von 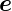 x. Der
Normalenvektor auf das Flächenelement steht senkrecht auf
d
x. Der
Normalenvektor auf das Flächenelement steht senkrecht auf
d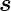 und
und 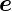 x. Also ist der Normalenvektor
x. Also ist der Normalenvektor
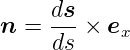
Die Fläche ist da = dsdx. Also erhalten wir
Mit C′·dx = Q′·dx∕u wird die Kapazität
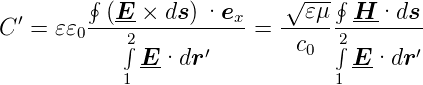 | (4.50) |
da 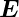 =
= 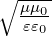
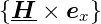 ist. Weiter haben wir die
Vektoridentität
ist. Weiter haben wir die
Vektoridentität
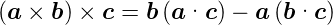
verwendet. Wir setzen 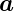 ≡
≡ 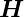 ,
, 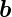 ≡
≡ 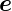 x und
x und 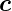 ≡ d
≡ d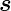 und
erhalten
und
erhalten
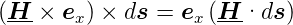
da 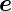 x ⊥d
x ⊥d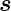 ist.
ist.
Um den Induktivitätsbelag zu ermitteln (siehe Abb. 4.150, rechts), berechnet man den Fluss ϕ zwischen der Stelle x und x + dx
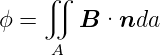 | (4.51) |
wobei über eine fiktive Fläche A zwischen den beiden Leitern integriert wurde. Das Flächenelement hat die Grösse da = dxdr. Der Normalenvektor wird durch
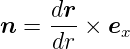
gegeben. Also ist
Da die Induktivität L längs der Strecke dx gegeben ist
durch L = L′·dx = ϕ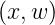 ·dx∕i(x,ω) folgt für den
Induktivitätsbelag
·dx∕i(x,ω) folgt für den
Induktivitätsbelag
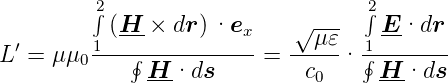 | (4.53) |
weil 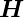 =
= 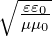
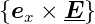 ist.
ist.
Für den Leitungswellenwiderstand erhalten wir
Weiter ist die Phasengeschwindigkeit
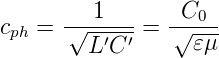 | (4.55) |
Die Leitung von elektromagnetischen Wellen bei hohen Frequenzen ist mit gewöhnlichen Kabeln nicht mehr möglich. Üblich für die niedrigeren Frequenzen sind Hohlleiter und für die ganz hohen Frequenzen Streifenleiter.
Einige Bauformen sind in der Abb. 4.151 dargestellt. Prinzipiell sind alle Bauformen möglich. In der Praxis werden jedoch nur
Die letzteren werden aber nur für sehr spezielle Leitungsprobleme verwendet, unter anderem da durch ihre hohe Symmetrie keine Polarisationserhaltung garantiert ist.
Aus den Maxwell-Gleichungen und den üblichen
Randbedingungen lassen sich leicht die möglichen
Wellenleitermoden bestimmen. Da die 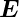 -Felder an
den Wänden eine Knotenlinie haben müssen, muss
transversal mindestens eine halbe Wellenlänge in
den Hohlleiter passen. Deshalb gibt es eine untere
Grenzfrequenz, unter der eine Wellenführung nicht möglich
ist11 .
Die unterste Mode (die mit der längsten Wellenlänge) in einem
rechteckförmigen Wellenleiter wird die TE10-Mode oder
auch die H10-Mode genannt. Die erste Bezeichnung stammt
daher, dass das
-Felder an
den Wänden eine Knotenlinie haben müssen, muss
transversal mindestens eine halbe Wellenlänge in
den Hohlleiter passen. Deshalb gibt es eine untere
Grenzfrequenz, unter der eine Wellenführung nicht möglich
ist11 .
Die unterste Mode (die mit der längsten Wellenlänge) in einem
rechteckförmigen Wellenleiter wird die TE10-Mode oder
auch die H10-Mode genannt. Die erste Bezeichnung stammt
daher, dass das 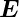 -Feld senkrecht zur Ausbreitungsrichtung
steht, also transversal ist. Die zweite Bezeichnung besagt, dass
das
-Feld senkrecht zur Ausbreitungsrichtung
steht, also transversal ist. Die zweite Bezeichnung besagt, dass
das 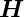 -Feld eine longitudinale Komponente hat, eine
Komponente die nur in einer geführten Welle existieren
kann. Bei beiden gibt der erste Index die Zahl der halben
Sinusbögen über der längeren Seite an, der zweite die Zahl der
halben Sinusbögen über der kürzeren Seite. Abb. 4.152 zeigt
die dazugehörigen Feldlinienbilder.
-Feld eine longitudinale Komponente hat, eine
Komponente die nur in einer geführten Welle existieren
kann. Bei beiden gibt der erste Index die Zahl der halben
Sinusbögen über der längeren Seite an, der zweite die Zahl der
halben Sinusbögen über der kürzeren Seite. Abb. 4.152 zeigt
die dazugehörigen Feldlinienbilder.
Durch die Wechselwirkung mit den Wänden ist die Wellenausbreitung in einem Wellenleiter dispersiv. Abb. 4.153 zeigt die Phasengeschwindigkeit als Funktion der Wellenlänge. Unterhalb der unteren Grenzfrequenz ωgr, bei der λ0∕2 = a ist, gibt es keine Wellenausbreitung. Die Amplitude wird exponentiell gedämpft. Oberhalb der der Grenzfrequenz wird die Wellenausbreitung durch die Wandströme und deren resistive Verluste gedämpft. Die Verluste sind für die Grundmode TE10 minimal. Die beste Transmission erreicht man mit supraleitenden Wellenleitern. Ab 2ωgr wird die TE20-Mode auch geführt. Typischerweise verwendet man bei Wellenleitern nicht den ganzen möglichen Bereich, in dem nur die Grundmode geführt wird, sondern nur 1.25·ωgr…1.9·ωgr. Die untere Grenzfrequenz rührt von den divergierenden Verlusten für ω → ωgr+ her, die obere von der Tatsache, dass auch unterhalb von 2ωgr die TE20-Mode eine merkbare Amplitude bekommt. Weiter ist in diesem Bereich die Änderung der Phasengeschwindigkeit minimal, die Dispersion also gering12 .
Für die Wellenlänge λL im Hohlleiter gilt die Formel
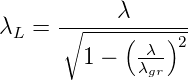 | (4.56) |
wobei λgr die zur Grenzfrequenz ωgr gehörige Wellenlänge ist.
Elektromagnetische Wellen werden einerseits durch die in den Hohlleitern vorhandene Luft, andererseits aber auch durch die Absorption in den Metallwänden der Hohlleiter oder in den Metallstreifen der Streifenleiter gegeben. Abb. 4.154 zeigt das Absorptionsspektrum in Luft. Bei tiefen Frequenzen ist es vor allem die Absorption durch Wasser und durch Sauerstoff (mit magnetischem Dipolmoment!), die dominiert. Im Infrarotbereich kommt die Absorption durch CO2 hinzu. Zwischen 14 und 8 μm ist ein Absorptionsfenster, wie auch zwischen 1100 und 300 nm.
Die Absorption steigt in Metall-Hohlleitern stark mit der Frequenz an. Zwei Gründe gibt es:
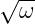 ab. Dadurch wird die
Wellenleitereigenschaft des Metalls schlechter (Siehe
Abb. 4.155).
ab. Dadurch wird die
Wellenleitereigenschaft des Metalls schlechter (Siehe
Abb. 4.155).
Insgesamt ergibt sich eine zu ω3∕2 proportionale Dämpfung13 .
Abb. 4.156 zeigt die Dämpfungseigenschaften für Wellenleiter. Das für viele physikalische Experimente wichtigste Frequenzband ist das X-Band zwischen 8.2 und 12.4GHz.
Für höhere Frequenzen verwendet man oft Streifenleiter. Sie können mit photolithographischen Verfahren hergestellt werden, sind also in kleinen Abmessungen wesentlich präziser herzustellen als die Hohlwellenleiter. Die Dämpfung ist im Allgemeinen höher bei Streifenleitern als bei Hohlleitern. Andererseits hat dies, zum Beispiel bei der Mobilkommunikation, wegen den geringen Grössen der Geräte, kaum einen Einfluss. Zusammen mit SMD-Bauteilen (Surface Mounted Device) lassen sich sehr effizient Mikrowellenschaltungen industriell herstellen. Der Streifenleiter in der Abb. 4.157 hat die folgenden Eigenschaften:
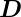 -Feldlinien darstellen.
-Feldlinien darstellen.
Im Gegensatz zu Hohlleitern gibt es bei Streifenleitern
sowohl beim 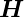 -Feld als auch beim
-Feld als auch beim 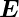 -Feld longitudinale
Komponenten. Dies rührt daher, dass an Grenzflächen neben der
Normalkomponente von
-Feld longitudinale
Komponenten. Dies rührt daher, dass an Grenzflächen neben der
Normalkomponente von 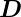 auch die Tangentialkomponente
von
auch die Tangentialkomponente
von 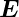 stetig sein muss. Man spricht deshalb von
Quasi-TEM-Moden oder von Hybrid-Moden.
stetig sein muss. Man spricht deshalb von
Quasi-TEM-Moden oder von Hybrid-Moden.
Bei dielektrischen Wellenleitern, zu denen auch optische Fasern gehören, werden Wellen im Medium mit dem grössten Brechungsindex geführt. Die Ausbreitungsgeschwindigkeit hängt von der Brechzahl ab, also cn = c0∕n. Beim Übergang vom optisch dichteren Medium mit n1 nach dem optisch dünneren Medium mit n2 < n1 kann bei flachem Einfall Totalreflexion auftreten. Das Snellius’sche Brechungsgesetz (siehe auch Abb. 4.158) lautet
für den gebrochenen sowie den reflektierten Strahl. Nach diesem Prinzip wird Licht in Multimoden-Wellenleitern geführt. Die unterschiedlichen Brechungsindizes werden mit Dotierstoffen erreicht. So vergrössert, zum Beispiel, eine Dotierung mit Ge den Brechungsindex. Eine Dotierung mit F verringert ihn.
Optische Wellenleiter werden in der Kommunikationstechnik vor allem wegen ihren geringen Verlusten14 (für eine Übersicht über den Dämpfungsverlauf siehe Abb. 4.159) und ihrer geringen Anfälligkeit auf externe Störungen. An der Universität Ulm hat ein Wellenleiter, der mitten durch einen Brand führte, während dem Brand anstandslos Daten übertragen!
Die Dämpfung bewirkt einen exponetiellen Abfall der übertragenen Leistung. Üblicherweise wird die Dämpfung α in dB (deziBel) angegeben. Der Leistungsabfall ist also
![P (z) = P ·10 αz[dB ]∕10
0](phys_elektr1094x.png) | (4.60) |
wobei P0 die Leistung am Eingang der Faser ist und α der Dämpfungsfaktor in dB. Die Dämpfung setzt sich aus drei Komponenten zusammen:
zusammen. Die Biegedämpfung rührt von der Krümmung der Glasfaser her und ist, zumindestens für Licht das über Totalreflexion geleitet wird, einfach zu verstehen. Wird das Kabel in einer zu engen Schleife gelegt, so ist die Bedingung der Totalreflexion nicht mehr erfüllt und die Verluste steigen. Zusätzlich zu dieser Makrodämpfung kommt die Mikrodämpfung, deren Ursache Spannungen in der Faser und Schwankungen in der Materialzusammensetzung, zum Beispiel durch eine nicht konstante Dichte der Dotierstoffe, sind.
Die Absorption hängt von der Reinheit des Materials ab. Insbesondere störend ist die OH−-Bande bei 1380 nm und bei 1240 nm sowie die Infrarotabsorption über 1600 nm.
Der hauptsächliche Dämpfungsmechanismus ist jedoch die Rayleigh-Streuung, die bis zu 95% der gesamten Dämpfung ausmacht. Sie rührt daher, dass im Glas mikroskopische Dichteschwankungen existieren, die sich aus Gründen der Thermodynamik auch nicht komplett eliminieren lassen, sowie wegen der notwendigen Dotierstoffe.
Abb. 4.160 zeigt Dämpfungsspektren von Gradientenfasern und von Einmodenfasern. Die Einmodenfaser (auch Monomode-Faser genannt) hat eine geringere Dämpfung, da ihr Kern weniger dotiert werden muss. Der starke anstieg der Dämpfung unter 1250 nm Wellenlänge rührt daher, dass die Faser für kurze Wellenlängen nicht mehr einmodig ist, dass also die Führungseigenschaften nicht mehr so perfekt sind. Infrarotabsorption, Rayleigh-Streuung und Wasserabsorption (OH−-Absorption) sind bei beiden Typen zu erkennen.
| Abbildung 4.161.: | Optische Wellenleiter (Glasfasern) werden in drei Kategorien eingeteilt: Stufenindexfasern, Gradientenindexfasern und Einmodenfasern. |
Es sind drei Typen von optischen Wellenleitern üblich (siehe auch Abb. 4.161)
Bei allen dreien kann das Indexprofil mit
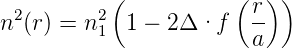 | (4.61) |
angegeben werden. Dabei ist a der Kernradius, r der Abstand vom Fasermittelpunkt und n1 der Brechungsindex im Kern. Δ ist die relative Brechzahldifferenz zwischen Kern und Mantel. Ausserhalb des Kerns, also für r > a hat man
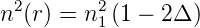 | (4.62) |
Diese allgemeine Funktion, die auch über den ganzen Faserquerschnitt gilt, ist für eine Stufenindexfaser
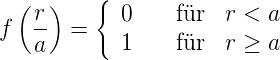 | (4.63) |
In der Stufenindexfaser werden alle Lichtstrahlen, für die sin α1 ≥N2∕n1 gilt total reflektiert, das heisst geführt[Pér96a]. Diese aus Abb. 4.162 ablesbare Bedingung kann auch als
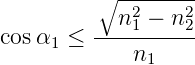 | (4.64) |
geschrieben werden. Strahlt man aus der Umgebung mit
dem Brechungsindex n0 Licht unter dem Winkel Θ0 ein, so
gilt an der Eintrittsfacette n0 sin Θ0 = n1 cos α1. Daraus folgt
n0 sin Θ0 ≤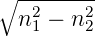 und somit
und somit
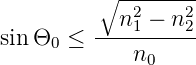 | (4.65) |
Damit werden alle Lichtstrahlen, für die die obige Bedingung gilt, geführt. Diese Bedingung ist aber auch äquivalent zur Definition der Numerischen Apertur eines Objektivs. Also sagt man, dass
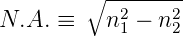 | (4.66) |
sei die numerische Apertur der Faser. Der maximale Wert von Θ0 heisst der Akzeptanzwinkel und ist
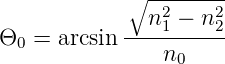 | (4.67) |
Für einen Brechungsindex des Kerns n1 = 1.57 und einen Brechungsindex des Mantels n2 = 1.51 in Luft (n0 = 1) ergibt sich N.A. = 0.43 und damit der Akzeptanzwinkel Θ0 = 25.50.
Wenn es darum geht, Licht aus einem räumlich eng begrenzten Gebiet mit einer relativ hohen numerischen Apertur zu sammeln, ohne dass eine Abbildung gewünscht wird, kann man vielfach anstelle von Linsen Fasern mit ähnlichen oder sogar grösseren numerischen Aperturen verwenden. Mit einigen Fasern lässt sich so sehr viel effizienter emittiertes Licht sammeln als mit einer einzelnen Linse.
In Gradientenindexfasern gilt für die Indexfunktion nach Gleichung (4.61) analog zu Gleichung (4.63)
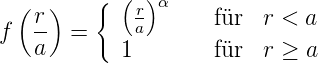 | (4.68) |
Dabei ist r der Abstand vom Kernzentrum. Der Unterschied im Brechungsindex in Gleichung (4.61) ist meistens klein, d.h. Δ « 1. Der Exponent ist andererseits häufig α = 2. Also kann für den Brechungsindex als Funktion der Position näherungsweise angenommen werden
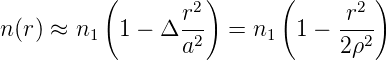 | (4.69) |
wobei ρ ≡a∕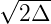 ist. Zur Berechnung der Bahnkurve
nehmen wir an, dass n1 entlang der Faser nicht variiert.
ist. Zur Berechnung der Bahnkurve
nehmen wir an, dass n1 entlang der Faser nicht variiert.
Um den Lichtweg, wie er in Abb. 4.163 angegeben ist, zu berechnen, gehen wir nach Pérez[Pér96a] von der vektoriellen Gleichung
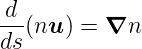 | (4.70) |
Mit der Gaussschen Näherung ds ∼dz erhält man für eine radiale Achse x
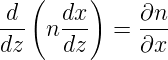 | (4.71) |
Mit
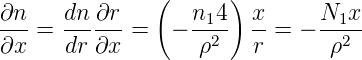
und da n1 nicht entlang der Faser (z!) nicht ändert, bekommt man
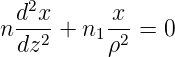 | (4.72) |
Da bei den meisten Glasfasern Δ « 1 ist ist auch n ≈n1. Deshalb erhält man schliesslich für die Differntialgleichung des Lichtweges
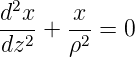 | (4.73) |
Der Lichtweg durch eine Gradientenindexfaser mit paraboloidem Indexprofil wird durch eine der Schwingungsgleichung ähnliche Gleichung beschrieben. Die allgemeine Lösung ist also
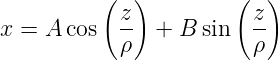 | (4.74) |
Zur Berechnung der Schwingungsform nehmen wir an, dass ein Lichtstrahl im Abstand xe von der Faserachse mit der Steigung xe′ = dxe∕dz in die Faser eintritt. Dann haben wir im Innern der Faser
Nach Pérez[Pér96a] kann damit die optische Transfermatrix bestimmt werden. Die Lösung für den speziellen Fall xe = 0 und n1xe′⇔ 0 ist
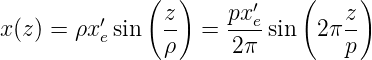 | (4.77) |
wobei p = 2πρ gesetzt wurde. Man ersieht aus Gleichung (4.77), dass alle Lichtstrahlen in Achsennähe sich periodisch im Abstand p schneiden15 .
Die numerische Apertur einer Gradientenfaser ist eine
Funktion von a, n1 und ρ = a∕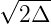 , also von der maximalen
Differenz des Brechungsindexes Δ. An der Eintrittsfläche
haben wir
, also von der maximalen
Differenz des Brechungsindexes Δ. An der Eintrittsfläche
haben wir
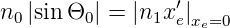
Die Bedingung, dass ein Lichtstrahl nicht aus dem Kernbereich herausläuft, also dass |x(z)|< a ∀z ist wegen |x| = |ρxe′ sin(z∕ρ)| ≤ |ρxe′| immer dann erfüllt, wenn |ρxe′|≤a ist. Dann gilt
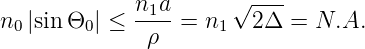 | (4.78) |
Damit ist die Numerische Apertur berechnet. Für eine Beispielfaser mit n1 = 1.57, einem Kerndurchmesser von a = 40μm und einem Indexsprung von Δ = 0.06 erhält man ρ = 115μm und damit die numerische Apertur N.A. = 0.54. Zur Illustration zeigt Abb. 4.163 ein gemessenes Brechzahlprofil. Der Knick unten links und rechts zeigt den Durchmesser des Kerns an. Der Dip in der Mitte ist produktionsbedingt.
Einmodenfasern Da die Kerne bei den Gradientenfasern und den Stufenindexfasern meistens so weit sind, dass mehrere Moden übertragen werden, können sie kurze Impulse im ns-Bereich oder kürzer nicht über lange Strecken übertragen. Lichtstrahlen, die unter verschiedenen Winkeln eintreten, legen unterschiedlich lange Wege zurück. damit verbreitern sich Impulse proportional zu der Länge der Faser. Wenn nun der Kerndurchmesser auf wenige Mikrometer verkleinert werden, kann die Faser nur noch eine Mode übertragen. Die Lösung des Laufzeitproblems erkauft man sich mit grossen Schwierigkeiten bei der Justage von Faserspleissen.
Einkopplung in optische Wellenleiter Zur Charakterisierung der Einkopplung verwendet man einerseits den Kopplungswirkungsgrad ηK = P2∕P1, der das Verhältnis von eingekoppelter Leistung zu angebotener Leistung anzeigt, oder, andererseits, die Kopplungsdämpfung αK = 10 lg(P2∕P1), die in dB gemessen wird.
Wenn eine Laserdiode oder eine LED in eine Faser gekoppelt wird, setzt man für P1 die Leistung des Senders ein. P2 ist dann die in der Faser transportierte Leistung. Der Kopplungswirkungsgrad zwischen optischem Sender und dem optischen Lichtwellenleiter hängt von folgenden Grössen ab:
Als Beispiel betrachten wir die Kopplung einer flächigen LED an einen Wellenleiter[BBH98]. Die LED wird als Lambert-Strahler modelliert.
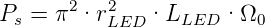 | (4.79) |
wobei rLED der Radius der emittierenden Fläche der LED ist, LLED die Strahldichte der LED und Ω0 der Raumwinkel, in den sie abstrahlt. Die in eine Gradientenfaser mit dem Profilparameter α eingestrahlte Leistung ist
![[ 2 ( r )α ]
PLW L = (π ·rmax ·N.A. )2·LLED · Ω0 · 1 − ------ -max-
α + 2 a](phys_elektr1118x.png) | (4.80) |
dabei ist
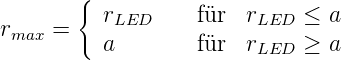
Wie weiter oben eingeführt ist a der Radius des Wellenleiterkerns, N.A. die numerische Apertur und α der Profilparameter. Aus den obigen Gleichungen errechnet man, dass der Koppelwirkungsgrad
![( ) [ ( ) ]
rmax- 2 --2--- rmax- α
ηK = rLED ·N.A. · 1 − 2 + α a](phys_elektr1120x.png) | (4.81) |
Wenn der Durchmesser des LED-Chips an den Durchmesser des Wellenleiters angepasst ist, erhält man
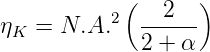 | (4.82) |
Damit bekommt man
| Wellenleitertyp | Kopplungswirkungsgrad |
| Stufenindexfaser (α →∞) | ηK = N.A.2 |
| Gradientenindexfaser (α = 2) | ηK = 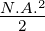 |
Man ersieht daraus, dass der Kopplungswirkungsgrad bei angepassten Durchmessern für Stufenprofilfasern mit N.A. = 0.5 ηK = 0.25 und für N.A. = 0.24 ηK = 0.0576 ist. Für Gradientenindexfasern mit dem gleichen Kerndurchmesser ist die Einkoppeleffizient jeweils halb so gross.
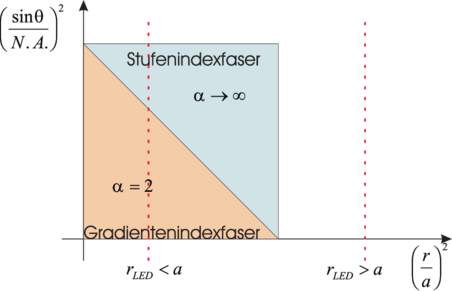
| Abbildung 4.165.: | Phasenraumdiagramm zur Abschätzung des Kopplungswirkungsgrades von optischen Wellenleitern. |
Der Kopplungswirkungsgrad kann über ein sogenanntes
Phasenraumdiagramm wie in Abb. 4.165 gezeigt, abgeschätzt
werden. Bei diesem wird der Sinus des Enfallswinkels relativ
zur numerischen Apertur quadriert (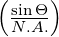 2 gegen die Fläche
der LED relativ zur Fläche des Wellenleiterkerns aufgetragen.
Man ersieht aus dem Diagramm, dass für den Fall dass der
Kerndurchmesser sehr gross wird, die Gradientenindexfaser
fast den gleichen
2 gegen die Fläche
der LED relativ zur Fläche des Wellenleiterkerns aufgetragen.
Man ersieht aus dem Diagramm, dass für den Fall dass der
Kerndurchmesser sehr gross wird, die Gradientenindexfaser
fast den gleichen
Kopplungswirkungsgrad hat wie die Stufenindexfaser.
Folgende Regeln können abgeleitet werden:
Neben der direkten End-zu End-Kopplung werden auch Koppeloptiken verwendet. Die Koppeldämpfungen der gebräuchlichsten Bauarten sind in der Tabelle 4.8 zusammengefasst.
| Art der Koppeloptik zwischen Sender und Faser | Koppeldämpfung |
| Stirnflächenkopplung | 5 dB …8 dB |
| Kugellinse oder Zylinderlinse | 1.5 dB …5 dB |
| Faserende dachförmig angeschliffen | 1.5 …2 dB |
| Faserende sphärisch angeschmolzen | 0.2 …1 dB |
| Faserende als taper ausgezogen | 0.2 …1 dB |
| Tabelle 4.8.: | Koppeldämpfung bei Faser-Faser-Kopplung |
Die Abbildung 4.166 zeigt den Einfluss von Fehlern auf die Koppeldämpfung dargstellt ist
Modenverteilung bei Glasfasern
Abb. 4.167 zeigt das Modenprofil eines Einmoden-Wellenleiters. Die Breite bei 1∕e ist hier etwa 10 μm. Abb. 4.168 zeigt den Felddurchmesser als Funktion desr Wellenlänge. Sehr schön sieht man den Einmodenbereich rechts mit einem Minimum kurz bevor die Faser zweimodig wird.
Wenn durch germaniumdotierte optische Wellenleiter hohe Leistungen gesandt werden kann das Licht Modulationen des Brechungsindexes im Faserkern erzeugen. Diese periodischen Störungen des Brechungsindexes wirken wie ein Bragg-Gitter, analog zur Streuung von Röntgenstrahlen in Kristallen. Heutzutage werden Faser-Bragg-Gitter als Sensoren und Spiegel verwendet[Oth97].
Herstellung Die Herstellung von Bragg-Gittern in Quarz-Fasern beruht auf der Lichtempfindlichkeit von Germanium-dotiertem Quarz. Ein einzelnes Photon (λ = 146nm) kann eine Indexändrung auslösen. Man glaubt, dass oxidierte Germanium-Dimere (O3Ge −GeO3) durch das Licht aufgespalten werden und dass sich so ein Farbzentrum bildet. Wichtig ist dabei, dass ein Sauerstoffdefizit um dieses Farbzentrum herrscht.
Die Photoempfindlichkeit kann gesteigert werden, indem die Faser mit Wasserstoff beladen wird, indem sie mit einer Wasserstoffflamme erhitzt werden und indem Bor zusätzlich zum Germanium dotiert wird.
In einem von verschiedenen diskutierten Modellen wird die Indexvariation im nahen Infrarot auf Absorptionsänderungen im ultravioletten zurückgeführt. Die dielektrische Funktion eines Materials besteht aus einem Realteil und einem Imaginärteil
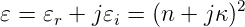 | (4.83) |
Dabei ist n der Brechungsindex und κ die Absorptionskonstante. Aus der Kausalität der Physik hatten Kramers und Kronig ihre Beziehung
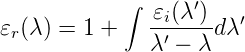 | (4.84) |
zwischen dem Real- und dem Imaginärteil abgeleitet. Wenn nun in einem Frequenzbereich der Imaginärteil (oder auch der Realteil) sich ändert, hat dies einen Einfluss auf den Realteil (oder Imaginärteil) bei allen anderen Frequenzbereichen. daraus kann man schliessen, dass ein Farbzentrum im UV-Bereich (ändert κ) den Brechungsindex im Infraroten beeinflusst. Da der Effekt im Imaginärteil über einen weiten Frequenzbereich im Realteil ausgeschmiert wird ist die Änderung des Brechungsindexes gering.
In einem anderen Modell wird angenommen, dass die durch die Photoionisation der Ge-Ge-Bindung freiwerdenenden Elektronen in der Nähe getrappt werden und so Dipolfelder erzeugen. Durch das statische elektrische Feld würden die Suszeptibilität dritter Ordnung moduliert werden und so die Variation des Brechungsindexes hervorrufen.
Ein drittes Modell nimmt an, dass durch die Wechselwirkung mit dem laserlicht die Dichte des Materials des Faserkerns verändert wird. Dadurch würden plastische Verformungen entstehen, die nicht mehr relaxieren könnten.
Ein viertes Modell schliesslich führt die Indexmodulation auf Spannungen zurück, die durch die UV-Beleuchtung entstanden seien. Dabei würde Zugspannung den Brechungsindex erniedrigen und Druckspannung ihn erhöhen.
Bragg-Gitter können entweder extern oder intern geschrieben werden. Eine häufige Methode bei der externen Generierung ist die Interferometrie. Abbildung 4.169 zeigt, wie man mit einem aufgespaltenen Strahl das Gitter herstellen kann. Die Bragg-Giterkonstante hängt vom halben Öffnungswinkel der beiden Strahlen φ sowie von der Wellenlänge λw des Schreibstrahls ab und ist
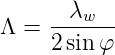 | (4.85) |
Die Bragg-Wellenlänge in der Faser ist λB = 2nΛ. Weiter der Abstand der Indexmaxima in der Faser gleich wie ausserhalb, da die Flächen gleicher Intensität senkrecht zur Faser stehen. Zusammenfassend ergibt sich für die Bragg-Wellenlänge also
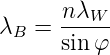 | (4.86) |
Bei einer Schreibwellenlänge von λW = 157nm, einem Winkel φ = 45°0 und einem Brechungsindex n = 1.5 wäre die Bragg-Wellenlänge λB = 333nm. Die interferometrische Methode nach Abb. 4.169 hat zum Vorteil, dass die Wellenlänge sehr leicht geändert werden kann. Nachteilig ist, dass der gesamte Aufbau interferometrische Stabilität benötigt.
Die in der Abb. 4.170 gezeigten Interferometer haben die notwendige Stabilität. Beide Interferometer sind sehr stabil, einfach herzustellen und haben einen einstellbaren Einfallswinkel. Anders als beim Prismenspektrometer geht das Licht beim Lloyd-Spektrometer nicht durch ein Dielektrikum. Dieses Spektrometer ist also weitgehend frei von Dispersionseffekten. Beide Spektrometer können nur Gitter von sehr beschränkter Länge in die Fasern einschreiben. Dies ist ihr hauptsächlicher Nachteil.
Wenn man Gitter mit variabler Tiefe oder Periode der Indexmodulation schreiben will, bedient man sich Häufig der Phasenmasken (Siehe auch abb. 4.171). Diese diffraktiven Masken können entweder holographisch oder lithographisch hergestellt werden. Die Phasenmasken werden so konstruiert, dass der Interferenzstrahl nullter Ordnung unterdrückt wird (Seine Intensität ist weniger als 5%) . Man versucht etwa 35 % der Intensität in die beiden ersten Ordnungen zu transferieren. Das Nahfeld-Interferenzmuster hat so eine Periode von der Hälfte der Periode der Phasenmaske (Talbot-Effekt). Eine Einführung in den Talboteffekt findet man in der Doktorarbeit von Eero Noponen17 [Nop94]. Durch die Fresnel-Beugung werden periodische Strukturen in ganzzahligen Vielfachen der Talbotdistanz
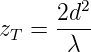 | (4.87) |
exakt abgebildet. Neben dem ganzzahligen Talboteffekt existiert auch der gebrochenzahlige. Mehrfache Bilder des ursprünglichen Gitters werden bei den Distanzen
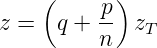 | (4.88) |
gebildet. Dabei sind n, p und q ganzzahlig. Zum Beispiel erhält man in der Distanz z = zT ∕(2 ∗ 2) = zT ∕4 zwei um eine halbe Gitterperiode gegeneinander verschobene Phasengitter, wenn das ursprüngliche Gitter ein Amplitudengitter war. Analog erhält man in diesem Abstand zwei um eine halbe wellenlänge gegeneinander verschobene Amplitudengitter, wenn das ursprüngliche Gitter ein Phasengitter war. Zum Beispiel würde ein Gitter der Periode d = 1μm, beleuchtet mit λ = 500nm eine Talbotdistanz von zT = 4μm haben. Das heisst, Im Abstand z = zT ∕4 = 1μm befindet sich nun ein Gitter mit der Periode 500nm.
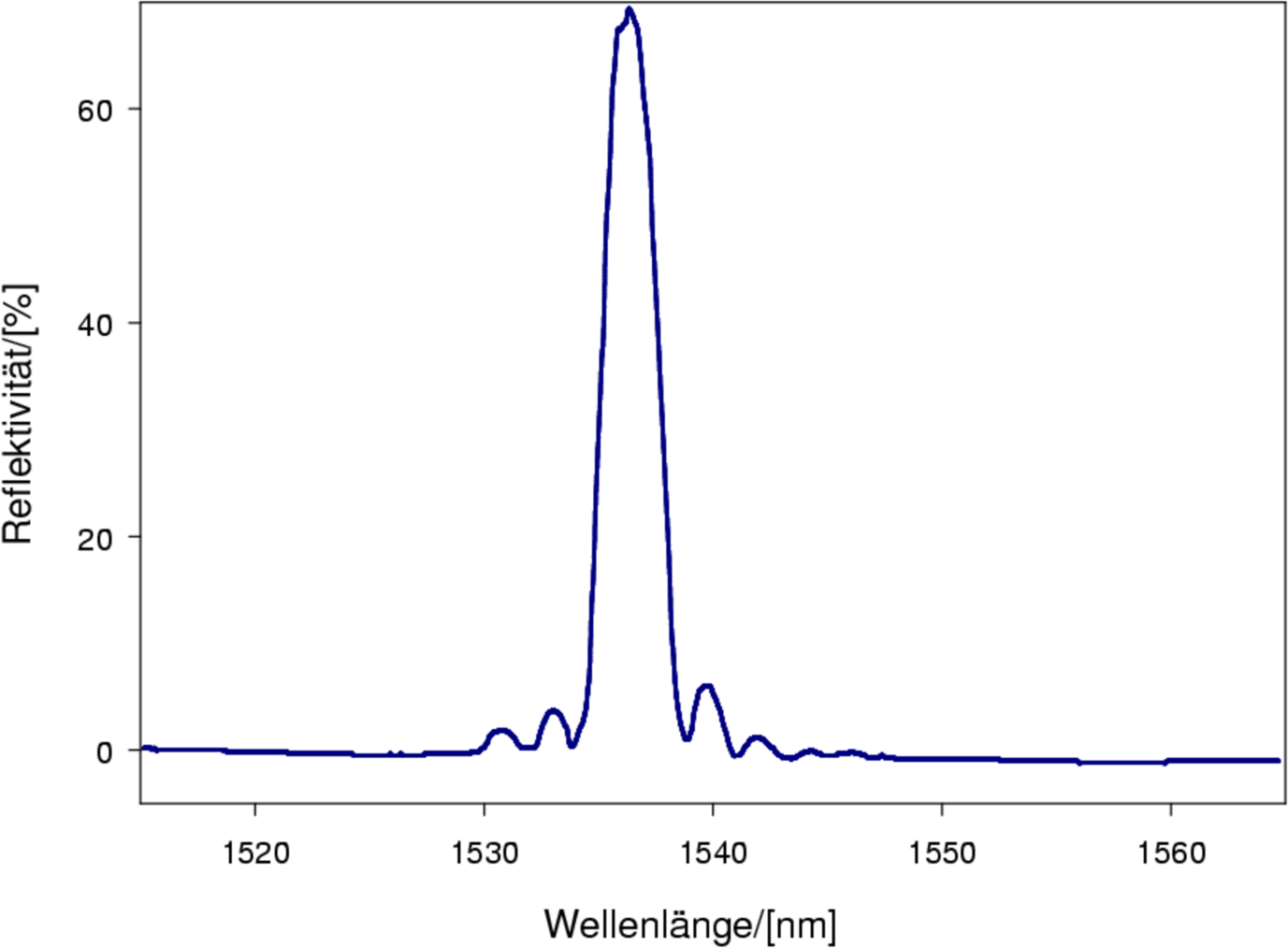
| Abbildung 4.172.: | Reflektionsspektrum eines Bragg-Gitters dritter Ordnung (Abbildung nach Malo et al.[MHB+93]. |
Durch eine Verkippung der Maske kann man, in Grenzen, die Periodendauer einstellen.
Die umfassendste Kontrolle über die Form des Gitters hat man, wenn man dieses mit einem konfokalen Laser-Scanning-Mikroskop schreibt. Dort kann man die Lage und die Modulationstiefe von jedem einzelnen Strahl einstellen. Abb. 4.172 zeigt ein Reflexionsspektrum eines so hergestellten Gitters.
Berechnung Die Streuung an Faser-Bragg-Gittern wird analog zur Braggstreuung in Kristallen behandelt[Oth97]. Die Energieerhaltung sagt, dass die Frequenz des einfallenden Lichtes ωi und jene des reflektierten Lichtes ωr gleich sein müssen. Die Impulserhaltung andererseits liefert die Bedingung, dass
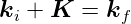 | (4.89) |
sein muss. Dabei ist 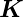 der Gittervektor mit |
der Gittervektor mit |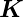 | = 2π∕Λ,
wobei Λ die Periodenlänge des Gitters ist.
| = 2π∕Λ,
wobei Λ die Periodenlänge des Gitters ist.
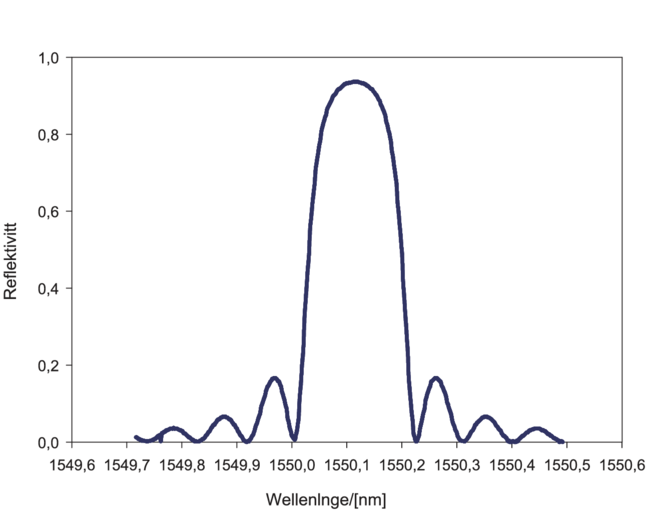
| Abbildung 4.173.: | Berechnetes Reflexionsspektrum eines Bragg-Gitters (Abbildung nach Othonos.[Oth97]). |
Da in einer optischen Faser die Ausbreitungsrichtungen vorgegeben sind (entlang einer Achse) erhält man aus Gleichung (4.89)
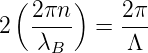 | (4.90) |
oder, vereinfacht
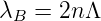 | (4.91) |
wobei λB die Wellenlänge des Lichtes im Vakuum und n der Brechungsindex der Faser im Kern ist. Wir nehmen nun an, dass das Bragg-Gitter über die Länge l die Brechzahlmodulation
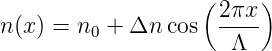 | (4.92) |
sei, wobei die Modulation Δn typischerweise 10−5…10−7 ist. Die Reflektivität des Bragg-Gitters ist nun
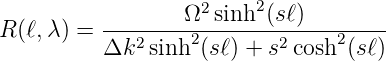 | (4.93) |
Die Reflektivität R(ℓ,λ) ist eine Funktion der Gitterlänge ℓ
und der Wellenlänge λ. Ω ist die Kopplungskonstante,
Δk = k −π∕λ ist der Wellenvektor der Verstimmung, k = 2πn0∕λ
ist der Wellenvektor des Lichtes und s = 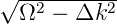 . Die
Kopplungskonstante ist
. Die
Kopplungskonstante ist
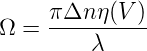 | (4.94) |
Hier ist η(V ) ≈ 1 − 1∕V 2, V ≥ 2.4, ist eine Funktion des Faserfüllfaktors V , der angibt, wieviel der Faserintensität der Grundmode im Kern (mit dem Bragg-Gitter) lokalisiert ist. Abb. 4.173 zeigt ein berechnetes Reflexionsspektrum. Auf der Mittenfrequenz des Bragg-Gitters ist Δk = 0. Also ist die Reflektivität
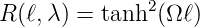 | (4.95) |
Die Halbwertsbreite des Reflexionsmaximums ist gegeben durch[Oth97]
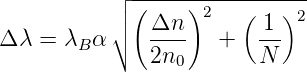 | (4.96) |
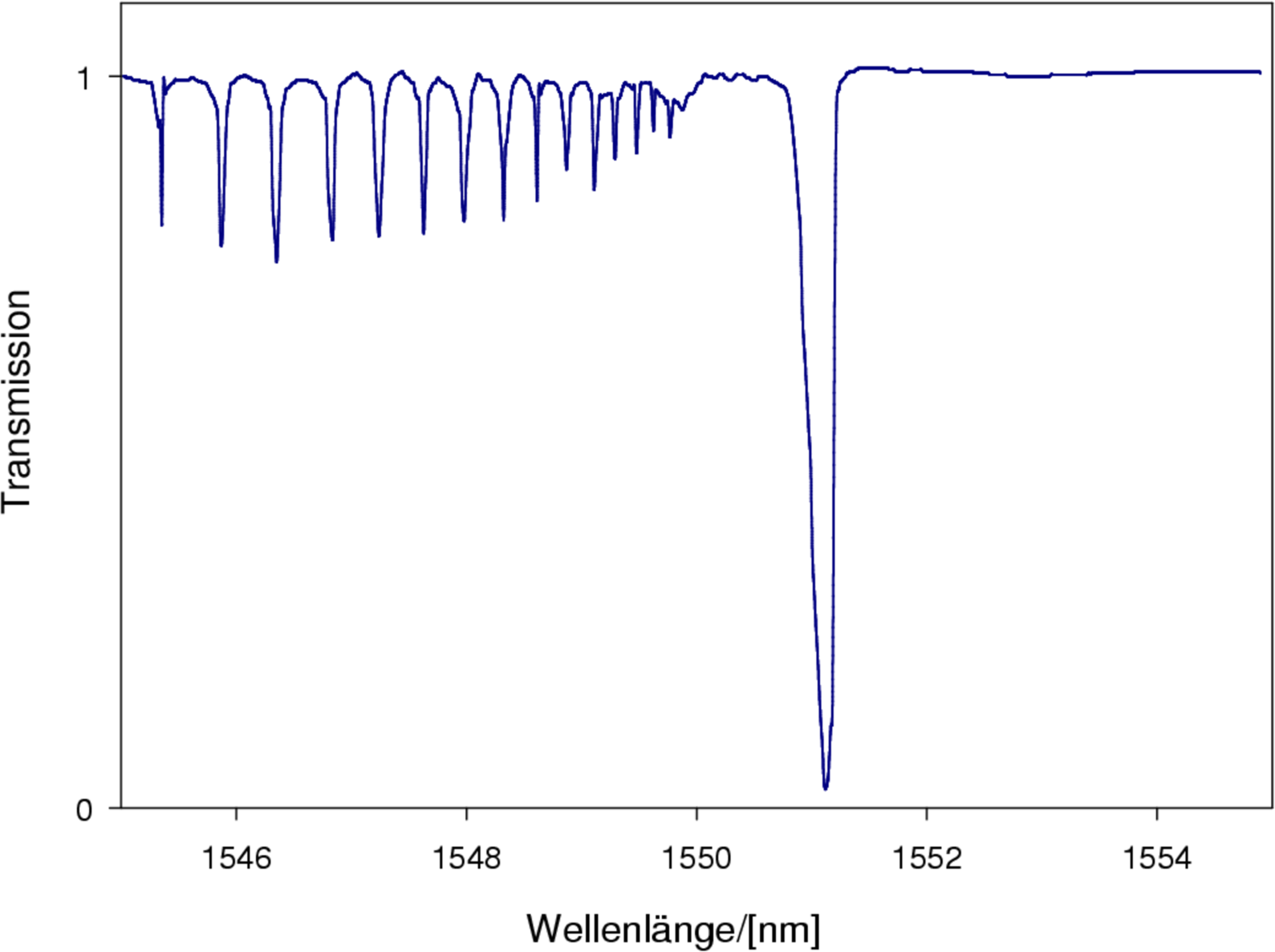
| Abbildung 4.174.: | Transmission durch ein starkes Bragg-Gitter. Dabei ist klar ersichtlich dass Strahlung in die Mantelmoden gekoppelt wird. (Abbildung nach Othonos[Oth97]). |
Abb. 4.174 zeigt, dass Bragg-Gitter die in sehr empfindliche Fasern geschrieben werden, die also eine starke Modulation des Brechungsindexes haben, auf der höherfrequenten seite des Bragg-Peaks ein ausgeprägtes Spektrum haben, das von Mantelmoden herrührt. Die spektralen Eigenschaften werden von Licht, das die Faser seitwärts verlässt, bestimmt.
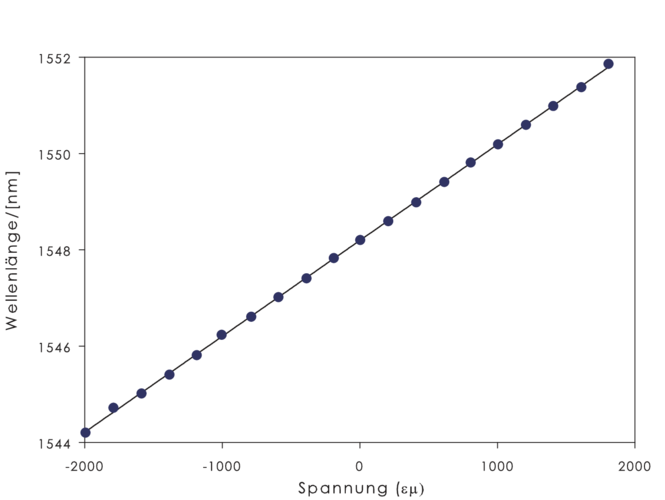
| Abbildung 4.175.: | Bragg-Wellenlänge eines Bragg-Gitters als Funktion der angelegten mechanischen Spannung (Abbildung nach Othonos[Oth97]). Das Bragg-Gitter war in eine Erbium-Dotierte Faser eingeschrieben und arbeitete als Auskoppelgitter. |
Die Mittenfreqquenz des Faser-Bragg-Gitters hängt vom Brechungsindex und der Periodenlänge ab. Beide Grössen werden jedoch durch externe Parameter verändert. Sowohl die Temperatur wie auch Zug auf die Faser können die Mittenfrequenz verschieben. Aus Gleichung (4.91) ermöglicht eine Berechnung der Verschieb3ung der Mittenwellenlänge des Gitters.
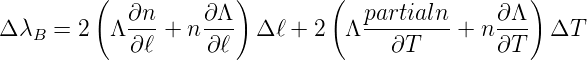 | (4.97) |
Der erste Summand in Gleichung (4.97) stellt den Einfluss von Zugspannungen dar (Eine Messung ist in Abb. 4.175 zu sehen). Man kann diesen Effekt auch als
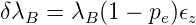 | (4.98) |
darstellen. In dieser Gleichung ist pe die effektive spannungsoptische Konstante. Sie ist wie folgt definiert:
![n2-
pe = 2 [p12 − ν(p11 + p12)]](phys_elektr1143x.png) | (4.99) |
Dabei sind p11 und p12 Komponenten des spannungsoptischen Tensors. n ist der Brechungsindex im Kern der Faser und ν ist die Poisson-Zahl. Bei einer typischen optischen Faser ist nach Othonos[Oth97] p11 = 0.113, p12 = 0.252, ν = 0.16 und n = 1.482. Man erwartet dann eine Empfindlichkeit von 0, 001pm für eine Spannung von 10−6.
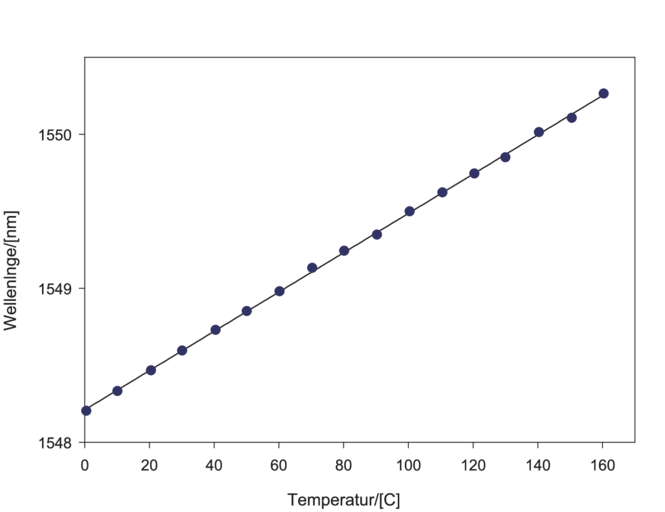
| Abbildung 4.176.: | Bragg-Wellenlänge eines Bragg-Gitters als Funktion der Temperatur (Abbildung nach Othonos[Oth97]). Das Bragg-Gitter war in eine Erbium-Dotierte Faser eingeschrieben und arbeitete als Auskoppelgitter. |
Der zweite Teil von Gleichung (4.97) beschreibt den Einfluss der Temperatur. Einerseits ändert die Temperatur den Abstand der Indexschwankungen, also die Periodenlänge, und andererseits ändert sich der Brechungsindex. Wir können für die Änderung der Bragg-Wellenlänge schreiben:
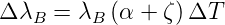 | (4.100) |
Dabei ist α = (1∕Λ)(∂Λ∕∂T) der thermische Ausdehnungskoeffizient18 und ζ = (1∕n)(∂n7∂T) der thermo-optische Koeffizient19 . Der Temperatureffekt ist also durch die Änderung des Brechungsindexes dominiert. Der Zahlenwert für Quarzglas ist 14 pm/°0C. Abb. 4.176 zeigt den Einfluss der Temperatur auf die Bragg-Wellenlänge eines Bragg-Gitters.
Die Änderung der Temperatur bewirkt nicht nur eine Verschiebung der Bragg-Wellenlänge, sondern auch eine Erniedrigung der Reflektivität, wie es schön aus Abbildung 4.177 ersichtlich ist.
Da jedes Bragg-Gitter in einer Faser mit mehreren Sensorstellen eine eigene, klar von den anderen trennbare Resonanzfrequenz haben kann, können einzelne Temperatur- oder Spannungssensoren über eine Auswahl der Wellenlänge adressiert werden.

| Abbildung 4.178.: | Zwei Bragg-Gitter als Fabry-Perot-Resonatoren. Rechts ist das Transmissionsspektrum gezeigt (Abbildung nach Othonos[Oth97]). |
Abb. 4.178 zeigt einen Fabry-Perot-Resonator in einer Faser. Der rechte Teil der Abbildung zeigt, dass dieses Fabry-Perot in einer Faser eine exzellente Linienbreite hat.
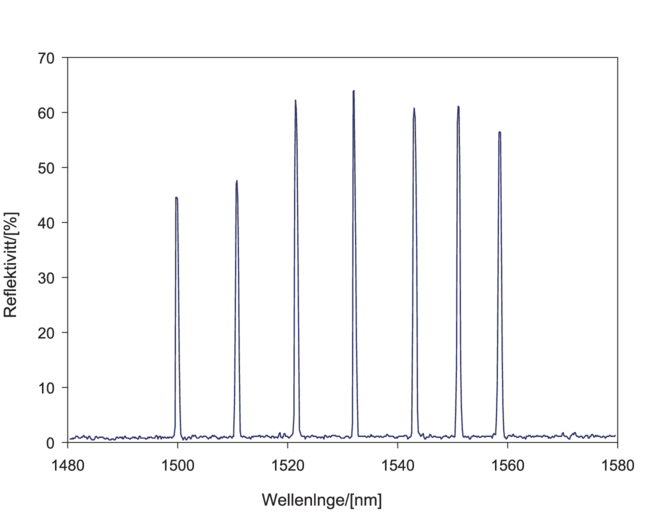
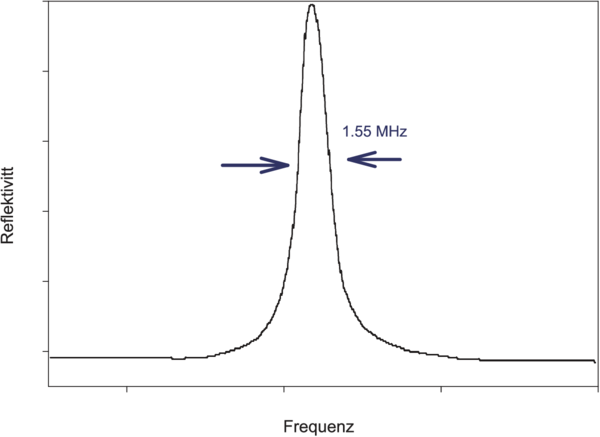
| Abbildung 4.179.: | Reflexionsspektrum für sieben am gleichen Ort eingebrannte Bragg-Gitter (Abbildung nach Othonos[OLM94]). |
Abb. 4.179 zeigt, dass man bei Faser-Bragg-Gittern mehrere Gitter übereinander einbringen kann. Dies ist einsichtig, wenn man bedenkt, dass ein Faser-Bragg-Gitter eigentlich mit Hologrammen verwandt ist. Auch bei Hologrammen können mehrere von ihnen in der gleichen Fotoschicht gespeichert werden. Mit Faser-Bragg-Gittern lassen sich so ganz neuartige Interferometer aufbauen.
 Lizenzinformationen
Lizenzinformationen