2.8  Rauschen

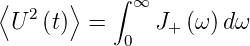
Mit Rauschen bezeichnet man die durch stochastische Prozesse bedingte Schwankung einer Grösse. Rauschen tritt nicht nur in der Elektronik auf, sondern in allen Vielteilchensystemen. So ist, zum Beispiel, die Brownsche Bewegung ein Rauschprozess. In der Elektronik betrachtet man den Transport von Strom, also einen Fluss einzelner Elektronen. Da diese, wie alle anderen Vielteilchensysteme den Gesetzen der statistischen Physik gehorchen müssen, tritt Rauschen auf. Man unterscheidet viele verschiedene Arten von Rauschen wie das Widerstandsrauschen oder das Schrotrauschen. In diesem Abschnitt soll zuerst das Widerstandsrauschen nach dem Buch von Reif[Rei65] abgeleitet werden, es folgen dann andere relevante Rauschprozesse.

2.8.1  Widerstandsrauschen

Wir betrachten einen elektrischen Widerstand R, der an den Eingang eines idealen Verstärkers angeschlossen sei, der zwischen ω₁ und ω₂ eine konstante Verstärkung habe. Ausserhalb dieses Durchlassbandes sei die Verstärkung 0.

Die Elektronen im Widerstand ändern ihre Position und Geschwindigkeit durch zufällige thermische Fluktuationen. Also existiert ein fluktuierender Strom I(t) und als Konsequenz auch eine fluktuierende EMF U(t). Wenn wir die Fouriertransformation von V (t) kennen, können wir nach Gleichung (2.17) die Varianz der EMF schreiben (Der Mittelwert der EMF ist null, da wir keine treibende Potentialdifferenz annehmen)

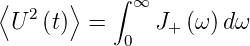(2.1)

Wie im Abschnitt 2.4.2.0.1 gezeigt, ist J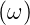₊ das Leistungsspektrum der EMF U(t). Reif [Rei65] zeigt im Abschnitt 15.8 mit der Langevin-Funktion, dass an einem Widerstand (analog zur Brownschen Bewegung) gilt

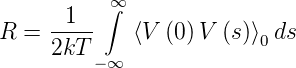(2.2)

Diese Gleichung kann mit den Gleichungen (2.19) und (2.17) umgeschrieben werden (die Korrelationsfunktion ist unabhängig von t, und e^jωs = 1 wenn ω = 0)

(2.3)

Die Korrelationszeit τ^∗ der Fluktuationen ist von der Grössenordnung der Zeit zwischen zwei Stössen eines Elektrons mit dem Gitter. Also ist K(s) = 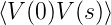₀ = 0 für alle 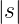»τ^∗. Die Korrelationsfunktion ist in der Nähe von 0 konzentriert. Also ist im Bereich der nichtverschwindenden Korrelationsfunktion e^jωs = 1 für alle ωτ^∗ « 1. Für alle diese ω-Werte hat das Integral den gleichen Wert

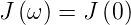(2.4)

Das Leistungsspektrum der fluktuierenden EMF U(t) ist also konstant. Man kann ziemlich allgemeingültig festhalten:

Diese Aussage ist übrigens analog zum Heisenbergschen Unschärfeprinzip.

Wir erhalten damit das Leistungsspektrum der Rausch-EMF an einem Widerstand

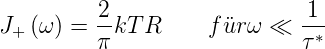(2.5)

Die obige Gleichung ist das Nyquist-Theorem. Es ist ein Spezialfall der viel allgemeineren Verbindung zwischen Fluktuation und Dissipation. Zum Beispiel gibt es bei der Brownschen Bewegung eine ähnliche Beziehung zwischen dem Spektrum der fluktuierenden Kraft F und dem Reibungskoeffizienten α. Interessierte Leser mögen Literatur über das ¨Fluktuations-Dissipations-Theorem¨ lesen. Rauschen mit einer von der Frequenz unabhängigen spektralen Dichte heisst weisses Rauschen.

Wir wollen nun untersuchen, ob das Nyquist-Theorem konsistent mit der Thermodynamik von Gleichgewichtszuständen ist. Wir verwenden dazu die Schaltung aus Abbildung 2.68. Das System sei im thermischen Gleichgewicht bei der Temperatur T. Stromfluktuationen I(t) haben ihre Ursache in der stochastischen EMF im Widerstand R. Wir betrachten die Fourierkomponente U₀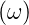 e^jωt der EMF und verwenden die Differentialgleichung

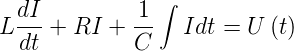(2.6)

Für die Frequenz ω erhält man

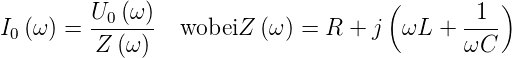(2.7)

Zur Berechnung der in der Induktivität gespeicherten Energie betrachtet man den Strom I als einen Parameter eines thermodynamischen Systems mit der freien Energie ΔF (Siehe auch das Buch von Reif[Rei65]). Die Wahrscheinlichkeit P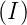 dI dass der Strom in einer Schaltung im Gleichgewicht mit der Temperatur T einen Wert zwischen I und I + dI annimmt, ist proportional zu e^ΔF∕kT . ΔF ist die freie Energie im Zustand I = 0. Die Bewegung von Elektronen, ohne dass Ladung auf- oder abgebaut wird, ändert die Entropie S nicht. Also ist ΔS = 0 und damit ΔF = ΔE −TΔS = ΔE. Da Energie durch einen Strom nur in einer Induktivität gespeichert werden kann, gilt:

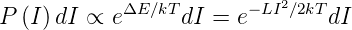(2.8)

Daraus leitet man unter Verwendung elementarer Gesetze der Statistik ab

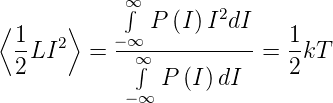(2.9)

Analog gilt auch für einen Kondensator, dass im Mittel im thermischen Gleichgewicht gilt

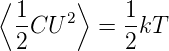(2.10)

Der Ausdruck für die mittlere in der Induktivität L gespeicherte Energie kann in eine Fourierreihe entwickelt werden:

Dabei haben wir die Definition des Leistungsspektrums nach Gleichung (2.29) verwendet.

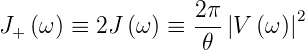(2.12)

Die Gleichgewichtsbedingung (2.9) verlangt, dass unter Verwendung von (2.7) gilt:

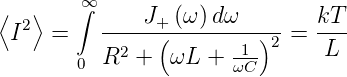(2.13)

Umgeformt mit ω₀² = 1∕LC bekommt man

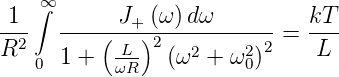(2.14)

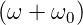
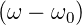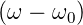Wir nehmen an, dass L sehr gross ist, dass also der Schwingkreis eine sehr grosse Güte hat. Dann kann man J₊ = J₊ aus dem Integral herausziehen. Ebenso ist dann ω² −ω ₀² = ≈ 2ω₀ und 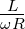≈ 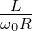. Mit der Abkürzung η = ω −ω₀ erhalten wir

Wir erhalten daraus das Resultat

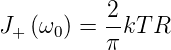(2.16)

Da C in der Gleichung nicht explizit vorkommt, kann man damit jede Frequenz erreichen, wir haben also, auf eine andere Art und Weise das Nyquist-Theorem abgeleitet.

In einem weiteren Beispiel wird, wie in Abbildung 2.69 im thermischen Gleichgewicht ein Widerstand R mit einer allgemeinen Impedanz Z′(ω) = R′(ω) + jX′(ω) zusammengeschaltet. Sowohl der Widerstand R′ wie auch der reaktive Teil X′ sollen frequenzabhängig sein. Wir bezeichnen mit U(t) die Spannung an R und mit U′(t) die Spannung an der Impedanz Z′. Im Gleichgewicht muss die mittlere Leistung P′, die durch die Impedanz Z′ wegen der Rauschspannung U(t) am Widerstand R absorbiert wird, gleich sein der Leistung P, die durch den Widerstand R wegen der Rauschspannung U′(t) der Impedanz Z′ absorbiert wird. Wir betrachten weiter ein enges Frequenzband zwischen ω und ω + dω. Das Leistungsgleichgewicht muss für alle Frequenzbänder gelten. Nun erzeugt die Frequenzkomponente U₀(ω) in der Schaltung den Strom I₀ = 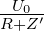Die Leistung P′ absorbiert durch Z′ ist dann

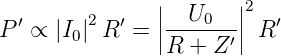(2.17)

R′ ist der (frequenzabhängige) Realteil der Impedanz Z′. Analog zur obigen Gleichung gilt auch

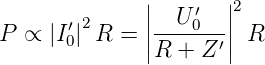(2.18)

Also ist

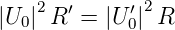(2.19)

oder

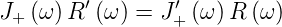(2.20)

J₊ ist das Leistungsspektrum von U(t) und J′₊ dasjenige von U′(t). Also ist

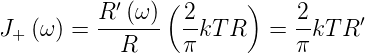(2.21)

Das Rauschspektrum einer jeglichen Impedanz ist also immer mit dem Widerstandsteil dieser Impedanz verbunden. Ideale Spulen und Kondensatoren rauschen nicht. Deshalb kann man mit Hilfe parametrisch veränderter Kapazitäten sehr rauscharme Verstärker bauen.

Nyquist hatte sein Theorem aus Analogien der Schwarzkörperstrahlung abgeleitet. Abbildung 2.70 zeigt die von ihm verwendete Anordnung. Zwei Widerstände der Grösse R sind über eine verlustfreie Leitung der Länge L mit der Impedanz R verbunden. Die ganze Anordnung ist im Gleichgewicht mit einem Wärmebad der Temperatur T. Durch die Impedanzanpassung wird jede vom linken Widerstand ausgehende Welle vom rechten vollständig absorbiert und umgekehrt. Die beiden Abschlusswiderstände sind also ein Analogon zum Schwarzen Körper. Eine Spannungswelle U = U₀e^j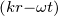 breitet sich mit der Geschwindigkeit c′ = 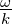aus. Zum Abzählen der möglichen Moden setzt man als Randbedingung U(0) = U(L). Dann ist kL = 2πn für jede ganze Zahl n. Die Anzahl Moden pro Einheitslänge im Frequenzintervall ω bis ω + dω ist dann

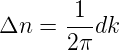(2.22)

Jede Mode hat eine Energie

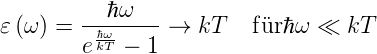(2.23)

Wir verwenden nun, dass im Gleichgewicht in jedem Frequenzintervall ω bis ω + dω die emittierte und die absorbierte Leistung eines Widerstandes gleich sein muss. Da es 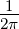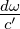propagierende Moden pro Einheitslänge gibt, ist die auf einen Widerstand eintreffende Leistung

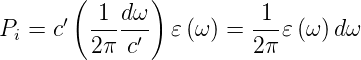(2.24)

Die emittierte Leistung ist gleich. Diese Leistung wird in Form einer Rauschspannung U erzeugt. Deshalb muss auch ein Strom I = 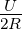fliessen. Wir müssen 2R verwenden, da der Generator der Rauschspannung die Serieschaltung zweier Widerstände R sieht. Also ist

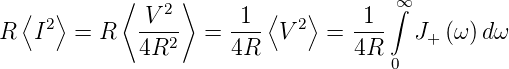(2.25)

Die Leistung im Frequenzintervall ω bis ω + dω ist dann

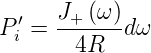(2.26)

Wenn man nun P′_i = P_i setzt, dann bekommt man

Dies ist die Gleichung für das Rauschen unter Einbezug der quantenmechanischen Korrekturen. Für die üblichen Frequenzen, auch im Mikrowellenbereich, gilt ℏω kT. Also wird aus Nyquists quantenmechanisch korrekter Formel

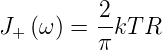(2.28)

Betrachtet man nun das Rauschen in einem bestimmten Frequenzband bei genügend tiefen Frequenzen, dann ist

wobei B = 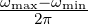die Bandbreite der Detektion ist.

Das Widerstandsrauschen ist besonders bei breitbandigen Schaltungen der limitierende Teil.

2.8.2  Weitere Rauschquellen

2.8.2.1. Schroteffekt

In Elektronenröhren ist die statistische Fluktuation des Emissionszeitpunktes von Elektronen aus der Kathode (Dies würde übrigens auch für Feldemissionskathoden gelten) Ursache eines Rauschens. Schottky hat für dieses Rauschen die folgende Formel angegeben:

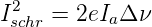(2.30)

I_a ist hier der Anodenstrom. Wie beim thermischen Rauschen ist die Ursache die Quantisierung der Ladung. Der Schroteffekt erlaubt, über eine Messung des Rauschstromes die Elementarladung zu bestimmen.

2.8.2.2. Generations-Rekombinationsrauschen

Dieser Typ Rauschen tritt in Halbleitern auf. Der Rauschstrom, der sich aus der diskreten Natur von Elektronen und Löchern ergibt ist:

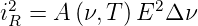(2.31)

E ist die elektrische Feldstärke im Kristall. A ist ein frequenz- und temperaturabhängiger Faktor.

2.8.2.3. Flickerrauschen und 1/f-Rauschen

Man beobachtet überall da wo Ladung transportiert wird ein Rauschspektrum, dessen Dichte sich wie

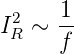(2.32)

verhält. Dieses Rauschen ist besonders bei langsamen Messungen sehr störend. Lock-In- Verstärker sind eine Möglichkeit, eine Messung aus dem mHz-Bereich, wo 1∕f-Rauschen dominant sein kann in den kHz-Bereich zu verschieben.

2.8.3  Einfluss von Filtern auf das Rauschen

Filter verändern die Rauschspannung anders als die Signalspannung (Siehe Dostal [Dos88]). Um den Effekt zu verstehen legen wir eine Rauschspannung mit dem Spektrum J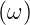₊ an den Eingang eines Filters mit der Übertragungsfunktion A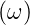. Das Signalspektrum J_s 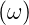wird durch das Filter wie folgt modifiziert:

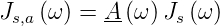(2.33)

betreibt man das obige Filter mit einer Rauschspannung, dann ist

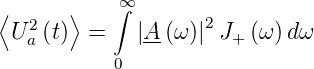(2.34)

Bei einer konstanten Verstärkung A₀ erhöht sich die Rauschspannung um den gleichen Wert A₀. Bei einem Filter, das mit weissem Rauschen gespiesen ist, kann man eine Rauschbandbreite definieren. Man nimmt (siehe Abbildung 2.71) an, man hätte ein Rechteckfilter mit der Verstärkung A_m und der Bandbreite ω_m bis ω_m + Δω_m. Nach dem Durchlauf dieses Filters soll die gemessene Rauschspannung gleich wie nach dem Passieren des zu untersuchenden Tiefpassfilters sein. Wir erhalten:

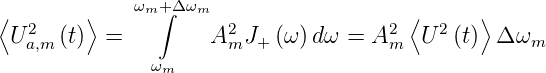(2.35)

Für weisses Rauschen findet man nun

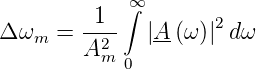(2.36)

Beim Tiefpass in Abbildung 2.71 ist die Übertragungsfunktion

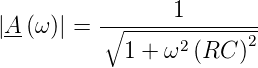(2.37)

Da die Verstärkung dieses Tiefpassfilters bei der Frequenz null den Wert eins hat, setzen wir A_m = 1 und erhalten

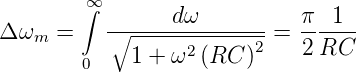(2.38)

Die Signalbandbreite des Filters ist definiert durch den 3dB-Abfall und gleich Δω_s = 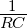. Die Rauschbandbreite ist also um den Faktor 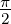grösser.

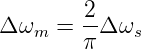(2.39)

Bei einem kritischen Tiefpass höherer Ordnung nähert sich die Signalbandbreite immer mehr der Rauschbandbreite. Ein Tiefpass m-ter Ordnung hat eine Übertragungsfunktion wie 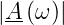= 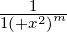. Das Integral zur Bestimmung der Rauschbandbreite hat die Rekursionslösung

Das Verhältnis von Rausch- zur Signalbandbreite ist in Tabelle 2.18 aufgelistet. Zusätzlich sind auch die Werte für ein Butterworthfilter aufgelistet. Der Leser kann sich anhand des oben beschriebenen Verfahrens die Rauschbandbreiten für andere Filter leicht selber berechnen.

Filterordnung m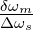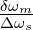
	Kritischer Tiefpass	Butterworth-Tiefpass
1	1,571	1,571
2	1,220	1,111
3	1,155	1,047
4	1,129	1,026
5	1,114	1,017
6	1,105	1,012
7	1,098	1,008
8	1,094	1,004

Tabelle 2.18.:

Verhältnis der Rausch- zur Signalbandbreite für kritische Filter und Butterworth-Filter