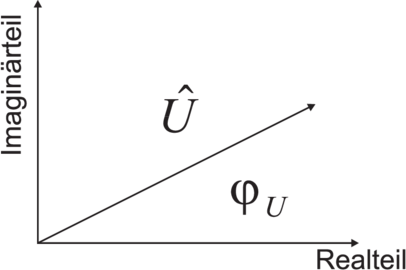

Bei der Besprechung von Übertragungsfunktionen gehen wir von der komplexen Darstellung aus[Ros83]. Eine Einführung in die Materie kann in A gefunden werden. Ausgehend von komplexen Amplituden, kann man eine Zeigerdarstellung für den Real- und Imaginärteil angeben.
Wenn nun bei einer komplexen Impedanz Z diese von einem Parameter p abhängt, so kann man eine Ortskurve zeichnen. Üblicherweise ist p = ω, es kann aber auch eine andere Grösse, z.B. die Kapazität bei einer Serienschaltung von Widerstand und Kondensator, sein. Bei Parallelschaltungen empfiehlt es sich, mit Leitwerten zu rechnen.
Ortskurven sind für Niederfrequenzanwendungen vielfach zu aufwendig zum berechnen. Es hat sich aber im Laufe der Jahre eingebürgert, dass Hochfrequenzanwendungen fast nur mit Hilfe von Ortskurven charakterisiert werden. Dies gilt z.B. auch für die Angabe des Frequenzverhaltens von Transistoren.
Abbildung 2.18 zeigt die Ortskurve für einen realen Parallelschwingkreis, bestehend aus einem Widerstand R, einer Spule L und einem Kondensator C. Die Impedanz der Schaltung aus 2.18 berechnet sich am einfachsten über den komplexen Leitwert Y .
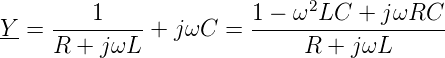 | (2.1) |
Man könnte mit dem Leitwert Y genau so gut eine Ortskurve darstellen (zum Teil ist dies bei Hochfrequenzanwendungen üblich), aber wir wollen hier die Impedanz Z verwenden.
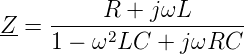 | (2.2) |
Mit den üblichen Abkürzungen ω0 = 1∕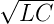 und
Ω = ω∕ω0 sowie Q =
und
Ω = ω∕ω0 sowie Q = 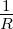
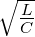 sowie nach der Normierung von Z
mit R wird
sowie nach der Normierung von Z
mit R wird
![[ ]
Z 1 + jΩ (1 − Ω2 )Q − 1-
-- = z-= ---------------(--)2-Q--
R (1 − Ω2 )2 + ΩQ-](phys_elektr23x.png) | (2.3) |
Real- und Imaginärteile sind dann
![--------1--------
Re (z(Ω )) = 22 (Ω-)2
(1 − Ω ) + Q
[ 2 -1]
Im (z(Ω )) = Ω--(1-−-Ω-)-Q(−-Q)-- (2.4)
(1 − Ω2)2 + Ω- 2
Q](phys_elektr24x.png)
![( )
Re z(Ω-) = --------1---------
Q2 (1 − Ω2)2 Q2 + Ω2
( ) [ 2 1]
z(Ω-) Ω--(1 −-Ω-)-Q-−-Q--
Im Q2 = 2 2 2 2 (2.5)
(1 − Ω ) Q + Ω](phys_elektr25x.png)
Die normierte Abbildung 2.19 zeigt schön, dass für grössere Q die Ortskurve zu einem Kreis wird. Es ist dem Leser überlassen, Ortskurven komplizierterer Schaltungen zu berechnen.
Wenn wir eine Schaltung mit Blöcken entsprechend dem Kapitel 2.1 haben, mit h(t) der Antwort des Systems auf einen Diracschen δ-Impuls ist, dann ist die Antwort auf eine allgemeine Anregung x(t) durch eine Faltung gegeben.
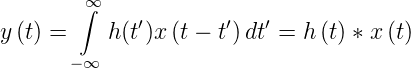 | (2.6) |
Beispiel (Maple-Datei): Ortskurven
 Lizenzinformationen
Lizenzinformationen