
(Siehe Reif, Statistical and Thermal Physics [Rei65, pp. 108])
Wir betrachten wieder zwei Systeme A und A′ im Kontakt. A habe die Energie E, A′ die Energie E′ = E0 -E, wobei E0 die Energie des gesamten Systems A0 = A + A′ sein soll. Wir entwickeln die Energie E um ihren Maximalwert Ẽ mit
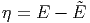 |
in eine Taylorreihe.
ln Ω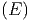 | = ln Ω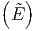 + + 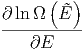 η + η + 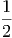 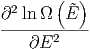 η2 + … η2 + … | ||
= ln Ω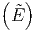 + βη - + βη -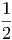 λη2 + … λη2 + … | (2.1) |
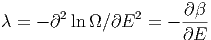 | (2.2) |
definiert.
Für das System A′ gilt
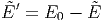 |
und damit
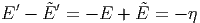 | (2.3) |
Damit bekommen wir
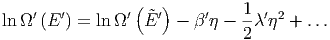 | (2.4) |
Wir addieren die beiden Gleichungen und erhalten
ln Ω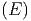 + ln Ω′ + ln Ω′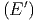 | ≈ ln Ω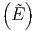 + βη - + βη - λη2 + ln Ω′ λη2 + ln Ω′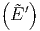 - β′η - - β′η -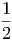 λ′η2 λ′η2 | ||
= ln 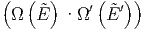 + η + η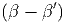 - -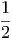 η2 η2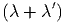 | (2.5) |
Dies ist eine quadratische Funktion in η. Damit diese ein Maximum hat, muss der Koeffizient von η null und der Koeffizient von η2 negativ sein. Deshalb gilt beim Maximalwert von Ω(E) = Ω(Ẽ)·Ω′(Ẽ′) (Die beiden Teilsysteme sind unabhängig!)
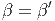 |
Dies bedeutet auch, dass die Temperaturen von A und A′ gleich sind.
Wir setzen λ0 = λ+λ′ und können für die Wahrscheinlichkeiten p(E) ∝ Ω(E) = Ω(Ẽ)·Ω′(Ẽ′) schreiben:
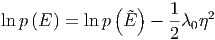 | (2.6) |
oder
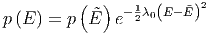 | (2.7) |
Die Grösse λ0 = λ + λ′ muss grösser null sein, da sonst p(E) kein Maximum hätte. Wenn wir eines der beiden Teilsysteme sehr viel kleiner als das andere wählen, muss auch das λ des grösseren Systems grösser null sein. Deshalb gilt auch λ > 0 und λ′ > 0.
Mit Ω = Ef folgt
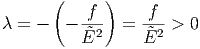 | (2.8) |
Die mittlere Energie eines Systems ist also die Energie des Maximums der Gaussverteilung.
Die Gaussverteilung selber ist gegeben durch
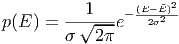 |
wobei σ die Standardabweichung ist. Der Vergleich mit Gleichung (2.7) ergibt:
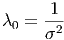 |
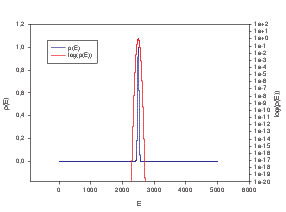
p(E) und ln(p(E)) für λ = 0.001 and Ẽ = 2500.
Weit ausserhalb des Maximums gilt
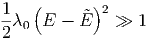 |
Dann ist
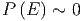 |
und
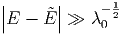 |
Die Breite der Verteilung, ΔE* = 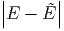 kann man dann
mit der Standardabweichung angeben, also
kann man dann
mit der Standardabweichung angeben, also
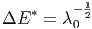 | (2.9) |
Wir betrachten zwei Systeme A und A′ im Kontakt. Das gesamte System sei A0 = A + A′. Wenn A » A′ ist, dann ist ist
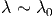 |
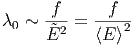 | (2.10) |
Wobei Ẽ die Energie des Maximums der Verteilung der
Zustände und 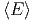 die mittlere Energie ist. Die Breite der
Verteilung ist dann
die mittlere Energie ist. Die Breite der
Verteilung ist dann
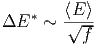 |
oder
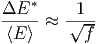 | (2.11) |
Bei einem Mol Teilchen (f ~ 1024) ist die Breite der
Verteilung 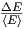 ≈ 10-12.
≈ 10-12.
 Lizenzinformationen
Lizenzinformationen