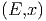 zwischen E und E + δE hängt nun von x ab. Sei x im
Intervall x → x + dx.
zwischen E und E + δE hängt nun von x ab. Sei x im
Intervall x → x + dx.

(Siehe Reif, Statistical and Thermal Physics [Rei65, pp. 112])
Wir lassen nun einen externen Parameter x zu. x könnte
zum Beispiel das Volumen V sein. Die Anzahl Zustände
Ω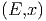 zwischen E und E + δE hängt nun von x ab. Sei x im
Intervall x → x + dx.
zwischen E und E + δE hängt nun von x ab. Sei x im
Intervall x → x + dx.
Wenn x sich um dx ändert, ändert sich die Energie des
Mikrozustandes Ei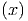 um den Wert
um den Wert 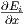 dx. Die Änderung
dx. Die Änderung 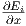 ist für jeden Zustand anders.
ist für jeden Zustand anders.
Wir nennen Ωy(E,x) die Anzahl Zustände zwischen E und
E + δE deren Ableitungen 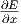 zwischen Y und Y + δY
liegen.
zwischen Y und Y + δY
liegen.
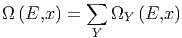 | (2.1) |
Wenn wir x um dx ändern, wie viele Zustände wechseln dann von einer Energie kleiner E zu einer Energie grösser als E?
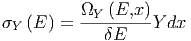 | (2.2) |
Die Summe über alle Zustände ist
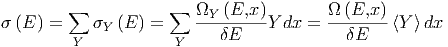 | (2.3) |
mit dem Mittelwert
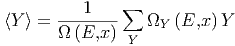 |
.
Wenn die Energie
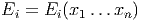 |
eine Funktion von x1…xn ist gilt für die Änderung der Energie des Zustandes i.
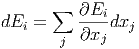 |
| In der Physik heisst die Grösse
die zur Variablen xj konjugierte „verallgemeinerte Kraft“. |
|
Zum Beispiel gilt dU = δQ - pdV und damit
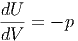 |
p ist also die zum Volumen konjugierte verallgemeinerte Kraft.
Analog erhalten wir mit Y = 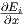 die Beziehung
die Beziehung
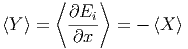 | (2.4) |
Die dazugehörige Arbeit δWi ist allgemein so definiert (Gleichung für totale Differentiale):
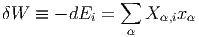 | (2.5) |
| Variable | verallgemeinerte Kraft |
| die Distanz x | die normale Kraft F |
| das Volumen V | der Druck p |
| die Oberfläche A | die Oberflächenspannung σS |
Wie ändert sich nun Ω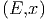 wenn x nach x + δx ändert?
σ(E) ist nach der Definition in Gleichung (2.2) die Zahl der
Moleküle von unterhalb E nach oberhalb E wechselt. Die
Grösse
wenn x nach x + δx ändert?
σ(E) ist nach der Definition in Gleichung (2.2) die Zahl der
Moleküle von unterhalb E nach oberhalb E wechselt. Die
Grösse 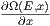 dx nimmt zu, weil σ(E) Zustände hinzukommen
und σ(E + δE) Zustände wegfallen. Die Bilanz ist (wir
verwenden die Definition der Ableitung)
dx nimmt zu, weil σ(E) Zustände hinzukommen
und σ(E + δE) Zustände wegfallen. Die Bilanz ist (wir
verwenden die Definition der Ableitung)
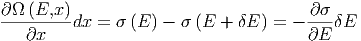 | (2.6) |
Aus Gleichung (2.3) bekommt man
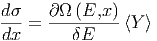 |
und damit
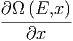 dx dx | = -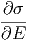 δE δE | ||
= -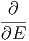 ![[ ]
Ω-(E,x-)-⟨Y⟩ dx
δE](td-2015667x.png) δE δE | |||
= -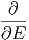 ![[Ω (E,x) ⟨Y⟩]](td-2015669x.png) dx dx | |||
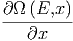 | = -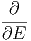 ![[Ω (E,x )⟨Y ⟩]](td-2015672x.png) | ||
= -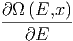 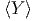 - Ω - Ω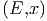 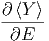 |
Wir teilen beide Seiten durch Ω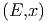 und bekommen
und bekommen
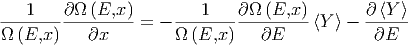 |
Diese Gleichung ist äquivalent zu
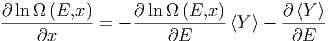 | (2.7) |
Wenn Ω ∝ Ef ist, ist der erste Summand 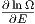
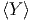 ∝
∝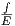
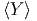 .
Den zweiten Summanden kann man abschätzen, wenn
man die Ableitung
.
Den zweiten Summanden kann man abschätzen, wenn
man die Ableitung 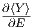 durch die Steigung der Gerade
zum Nullpunkt
durch die Steigung der Gerade
zum Nullpunkt 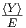 ersetzt. Dann ist der erste Summand
auf der rechten Seite der Gleichung für grosse Systeme
(f ⋙ 1) um den Faktor f grösser als der zweite Summand.
Der zweite Summand
ersetzt. Dann ist der erste Summand
auf der rechten Seite der Gleichung für grosse Systeme
(f ⋙ 1) um den Faktor f grösser als der zweite Summand.
Der zweite Summand 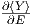 kann deshalb vernachlässigt
werden. Mit β(E) =
kann deshalb vernachlässigt
werden. Mit β(E) = 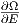 und Gleichung (2.4) bekommt
man
und Gleichung (2.4) bekommt
man
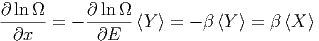 | (2.8) |
Diese formale Beziehung soll nun anhand von Beispielen erläutert werden.
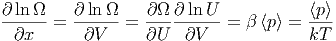 | (2.9) |
da ja nach dem 1. Hauptsatz für die innere Energie gilt
dU = δQ - pdV und damit 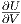 = -p. Gemittelt
bekommen wir also
= -p. Gemittelt
bekommen wir also 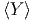 =
= 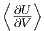 und
und 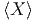 =
= 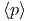 .
.
Bei mehreren externen Parametern modifiziert sich Gleichung (2.8) zu
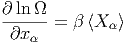 |
Wir betrachten ein isoliertes System A0 = A + A′, das aus zwei Teilsystemen besteht. Das Volumen V ist vom Volumen V ′ durch einen beweglichen Kolben getrennt. Die Gesamtenergie sei konstant: E0 = E + E′ = const, wie auch das Gesamtvolumen V 0 = V + V ′ = const. Die beiden Systeme tauschen Wärme und mechanische Arbeit aus.
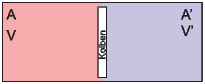
Skizze eines gekoppelten Systems, das durch einen Kolben getrennt ist.
Wir betrachten eine infinitesimale Änderung des Zustandes mit den externen Parametern xα und verwenden Gleichung (2.8) (verallgemeinerte Kräfte)
| d ln Ω | = 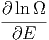 d d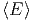 + ∑
α=1n + ∑
α=1n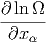 d d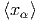 | ||
= β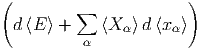 | (2.10) |
In unserem Falle ist xα = V und E = U die innere Energie. Somit erhalten wir mit δW = -pdV für unseren infinitesimalen Prozess
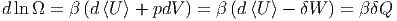 | (2.11) |
was nichts anderes als der erste Hauptsatz ist.
Wir können für infinitesimale Prozesse auch schreiben
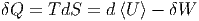 | (2.12) |
Bei einem adiabatischen Prozess ist δQ = 0 und damit dS = 0. Somit ändert sich auch Ω bei einem adiabatischen Prozess nicht!
Das Gleichgewicht ist erreicht, wenn die Wahrscheinlichkeit
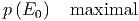 |
ist.
Die Anzahl Zustände des Gesamtsystems sind
Ω0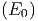 | = Ω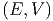 Ω′ Ω′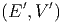 | ||
| ln Ω0 | = ln Ω + ln Ω′ | ||
| (2.13) |
| S0 | = S + S′ | (2.14) |
Das Maximum der Wahrscheinlichkeit, der Anzahl Zustände Ω und damit der Entropie S wird erreicht, wenn
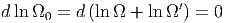 | (2.15) |
ist. Andererseits kann man für Änderungen der Anzahl Zustände als Funktion kleiner Änderungen dE oder dV auch schreiben
| d ln Ω | = 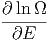 dE + dE + 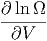 dV dV | ||
= βdE + β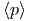 dV dV | (2.16) |
Analog erhält man für das zweite Teilsystem A′
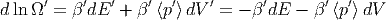 | (2.17) |
Wir haben dabei wegen der Energieerhaltung dE = -dE′ und wegen der Volumenerhaltung dV = -dV ′ geschrieben. Die Summe der Gleichungen 2.16 und 2.17 ergibt
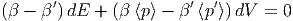 | (2.18) |
Dies muss für beliebige dE und dV gelten. Darum haben wir
| β - β′ | = 0 | ⇒ | β | = β′ | ⇒ | T | = T′ | (2.19) | ||
β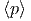 - β′ - β′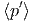 | = 0 | ⇒ | 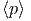 | = 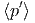 | (2.20) |
Dies sind die erwarteten Gleichgewichtsbedingungen, aber nun mit statistischen Argumenten hergeleitet.
 Lizenzinformationen
Lizenzinformationen