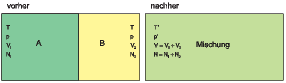
System aus zwei Molekülsorten A und B (links) und nach Mischung.


System aus zwei Molekülsorten A und B (links) und nach Mischung.
Wir betrachten nun ein Gesamtsystem, bei dem zu Beginn zwei Molekülsorten A und B in zwei getrennten Kompartimenten mit den Volumina V 1 und V 2 befinden. Es gibt jeweils N1 und N2 Teilchen von der jeweiligen Sorte. Die Grösse des Gesamtvolumens V 1 + V 2 = V sowie die gesamte Teilchenzahl N1 + N2 = N sollen konstant sein3 . Die Trennwand zwischen den beiden Kompartimenten sei beweglich, so dass sowohl die Temperatur T wie auch der Druck p konstant sind. Wir hatten früher die Mischung von identischen Teilchen betrachtet oder das Ausströmen von Teilchen ins andere Teilvolumen betrachtet. Hier versuchen wir zum ersten mal, die Eigenschaften eines Gemisches mit zwei Teilchensorten zu verstehen.
Beide Moleküle sollen ideale Gase sein. Aus der idealen Gasgleichung wissen wir, dass pV = NkT sein muss. bei gleicher Temperatur T und gleichem Druck p folgt
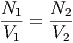 |
Wenn sich nach der Mischung alle Moleküle vom Typ A im linken Kompartiment 1 mit V 1 befinden, ist die Entropie um
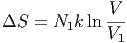 |
zu klein sein.
Mit
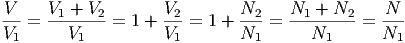 |
Also können wir die Entropiedifferenz auch mit den Teilchenzahlen schreiben.
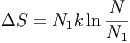 | (2.1) |
Die Mischungsentropie ist die Summe aus den Entropieänderungen wenn sich jeweils die Molekülsorte A in V 1 und B in V 2 befinden.
Beispiel:
Wir mischen zwei Molekülsorten mit gleichen Anteilen. Sei N1 = N2 = NA. Beispielsweise könnten wir He und Ne mischen.
| SM | = k·NA·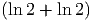 | ||
≈ 1.38·10-23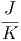 ·6·1023·2·0.63 ·6·1023·2·0.63 | |||
≈ 13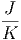 | (2.3) |
Beispiel:
Silizium soll mit 1ppm (1 part per million) verunreinigt sein. Wir wollen die Mischungsentropie für 1mol Si berechnen
| N1 | = NA | ||
| N2 | = 10-6N A |
Sie ist
| SM | = k·NA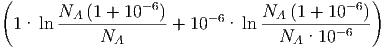 | ||
| ≈ k·NA·10-6 ln 106 | |||
| = k·NA·2.3·10-6·6 | |||
≈ 1.2·10-4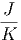 | (2.4) |
Wir wenden hier die Methode nach dem dritten Hauptsatz an. Wir wollen die Differenz der Entropie einer Legierung vor und nach dem Vorgang bestimmen. Für reversible Vorgänge (immer im Gleichgewicht) gilt
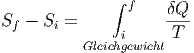 |
Entropien sind eine Funktion der Temperatur. Wir drücken sie mit den Wärmekapazitäten Cy aus, wobei y entweder den konstanten Druck (y ≜ p) oder das konstante Volumen (y ≜ V ) meint.
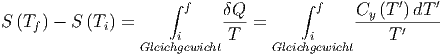 | (2.5) |
Wenn der betrachtete Temperaturbereich genügend klein ist, ist Cy in guter Näherung unabhängig von T. Dann können die Integrale gelöst werden
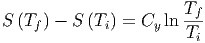 | (2.6) |
Wir wollen nun das praktische Beispiel berechnen, wie gross
die Entropiezunahme bei der chemischen Verbindung PbS ist.
Wir nehmen dazu an, dass wir für Pb, S und PbS die
Wärmekapazitäten Cy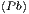
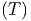 , C
y
, C
y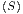
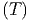 und C
y
und C
y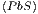
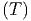 kennen. Nach dem dritten Hauptsatz ist geht die Entropie bei
T → 0 zu einem festen Wert S0, unabhängig von der genauen
Anfangskonfiguration und den Systemparametern. Wir
können also schreiben
kennen. Nach dem dritten Hauptsatz ist geht die Entropie bei
T → 0 zu einem festen Wert S0, unabhängig von der genauen
Anfangskonfiguration und den Systemparametern. Wir
können also schreiben
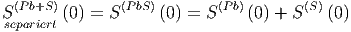 | (2.7) |
Mit den Entropiegleichungen für die Ausgangsmaterialien Pb und S
S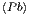 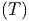 | = S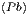 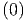 + ∫
0T + ∫
0T 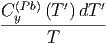 | ||
S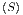 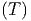 | = S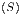 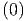 + ∫
0T + ∫
0T 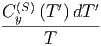 |
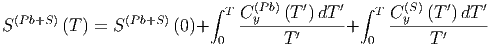 | (2.8) |
Die Entropiegleichung gilt natürlich auch für die Verbindung
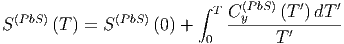 |
Mit Gleichung (2.7) können wir die Entropiedifferenz berechnen
S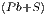 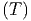 - S - S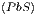 = = | ∫
0T 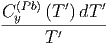 + ∫
0T + ∫
0T 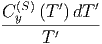 | ||
-∫
0T 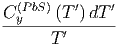 | |||
| = | ∫
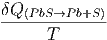 | (2.9) |
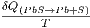 zwischen
Entropie und Wärmemenge verwendet.
zwischen
Entropie und Wärmemenge verwendet.
Die Gleichung (2.9) erlaubt uns nun, die benötigte Energie zur Dissoziation PbS in Pb und S vorherzusagen. Dazu braucht man „nur“ die Wärmekapazitätend Cy der beteiligten Stoffe zu kennen. Das Verfahren kann auf alle Verbindungen angewendet werden. Es zeigt, ob eine Verbindung stabil ist.
 Lizenzinformationen
Lizenzinformationen