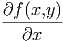

Dieser Abschnitt benutzt die Differentiationsregeln für Funktionen mehrerer Variablen. Wir betrachten eine Funktion f(x,y). Die in der Mathematik übliche Schreibweise einer partiellen Ableitung
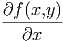 |
sagt implizit, dass die Grösse y beim Ableiten konstant gehalten wird. In der Wärmelehre ist es auch üblich, partielle Ableitungen wie
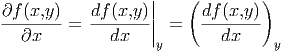 |
zu schreiben.
So ist die Wärmekapazität bei konstantem y durch
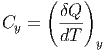 | (2.1) |
gegeben. Es gilt aber auch
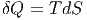 | (2.2) |
und damit
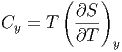 | (2.3) |
Als Beispiel berechnen wir die Wärmekapazität bei konstantem Volumen:
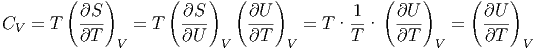 | (2.4) |
Dabei haben wir den ersten Hauptsatz dU = TdS - pdV
verwendet, der bei konstantem Volumen auch 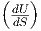 V = T
heisst.
V = T
heisst.
Der 1. Hauptsatz lautet
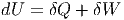 |
oder umgeschrieben
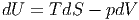 |
Diese Schreibweise bedeutet, dass S und V die unabhängigen Variablen sind.
Im Folgenden soll für ein ideales Gas
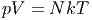 | (2.5) |
die Beziehung zwischen Ableitungen der Entropie berechnet werden.
Für die innere Energie gilt allgemein:
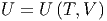 | (2.6) |
Damit kann man das totale Differential dU schreiben als
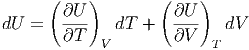 | (2.7) |
Aus dem 1. Hauptsatz und der idealen Gasgleichung erhalten wir
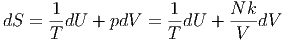 | (2.8) |
Das totale Differential dU wird durch den Ausdruck aus Gleichung (2.7) ersetzt. Wir erhalten
![1 ( ∂U ) [1 ( ∂U ) N k ]
dS = -- ---- dT + -- ---- + ---- dV
T ∂T V T ∂V T V](td-2015833x.png) | (2.9) |
Da dS ein totales Differential ist, muss für S = S(T,V ) gelten
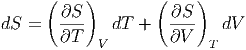 | (2.10) |
Diese beiden Beziehungen müssen für alle dT und dV gelten. Deshalb müssen die Vorfaktoren einzeln gleich sein:
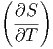 V V | = 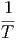 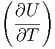 V V | (2.11) |
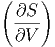 T T | = 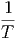 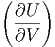 T + T + 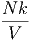 | (2.12) |
Wir betrachten nun die zweiten Ableitungen. Für gemischte Ableitungen gilt immer.
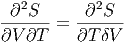 | (2.13) |
Wenn wir bei dieser Beziehung die ersten Ableitungen der Entropie mit ihren äquivalenten Grössen einsetzen, erhalten wir
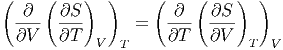 | (2.14) |
Wir ersetzen auf der linken Seite 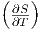 V mit Gleichung
(2.11) und auf der rechten Seite
V mit Gleichung
(2.11) und auf der rechten Seite 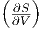 T mit Gleichung (2.12)
und erhalten
T mit Gleichung (2.12)
und erhalten
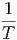 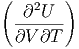 | = ![( [ ( ) ])
-∂- 1- ∂U-- + N-k-
∂T T ∂V T V](td-2015848x.png) V V | ||
= -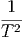 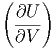 T + T + 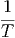 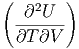 + 0 + 0 | (2.15) |
Die Ableitung ist null (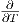
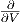
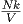 = 0), da Nk∕V nicht von T
abhängt.
= 0), da Nk∕V nicht von T
abhängt.
Deshalb gilt
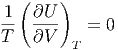 |
Wenn T < ∞ ist, gilt auch
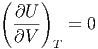 | (2.16) |
oder, in anderen Worten: die innere Energie hängt nicht vom Volumen ab!
 Lizenzinformationen
Lizenzinformationen