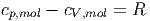

Wir suchen einen Zusammenhang für Cp und CV für beliebige Substanzen und beliebige Zustandsdichten Ω(E). Wir kennen für höhere Temperaturen und ideale Gase den Zusammenhang der molaren Grössen
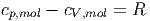 |
Hier möchten wir nun einen Zusammenhang ableiten, der nur von makroskopisch messbaren Eigenschaften abhängt. Konkret suchen wir eine Beziehung, die den spezifischen Volumenausdehnungskoeffizienten α und die isotherme Kompressibilität κ enthält. Wir beginnen mit den Definitionen der Wärmekapazitäten
| CV | = 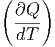 V = T V = T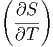 V V | ||
| Cp | = 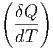 p = T p = T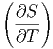 p p | (2.1) |
Die Entropie soll S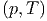 vom Druck und der Temperatur
abhängen. Dann gilt für die ausgetauschte Wärmemenge
vom Druck und der Temperatur
abhängen. Dann gilt für die ausgetauschte Wärmemenge
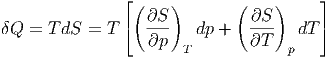 | (2.2) |
Wir setzen die Definition von Cp ein und erhalten
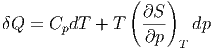 | (2.3) |
Wir teilen nun Gleichung (2.3) durch dT und erhalten
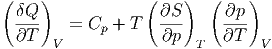 | (2.4) |
Der zweite Summand muss bei konstantem Volumen betrachtet werden, da ja nun p nicht mehr eine Variable sondern eine Funktion ist. Die ist auch im Einklang mit der Tatsache, dass wir ja noch eine Beziehung für die Wärmekapazität bei konstantem Volumen benötigen.
Zur weiteren Berechnung drücken wir dp als Funktion von T,V aus
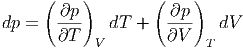 | (2.5) |
Da wir CV suchen, ist das Volumen konstant, der zweite
Summand in Gleichung (2.5), 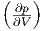 T dV , ist gleich null. Wir
erhalten also für CV
T dV , ist gleich null. Wir
erhalten also für CV
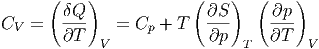 | (2.6) |
Mit der Maxwellrelation
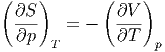 |
können wir Gleichung (2.6) umschreiben und erhalten
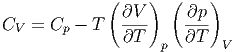 | (2.7) |
Wir ersetzen nun die beiden partiellen Ableitungen durch den Volumenausdehnungskoeffizienten α und die isotherme Kompressibilität κ. Die Definition des Volumenausdehnungskoeffizienten lautet
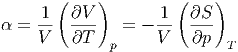 | (2.8) |
Damit kann 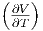 p umgeschrieben werden. Um
p umgeschrieben werden. Um 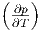 V (bei
konstantem Volumen, d.h. dV = 0!) umzuschreiben setzen wir
an
V (bei
konstantem Volumen, d.h. dV = 0!) umzuschreiben setzen wir
an
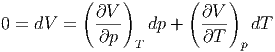 |
Diese Gleichung kann umgeschrieben werden
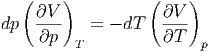 |
Wir teilen durch dT und bringen alle partiellen Ableitungen auf die rechte Seite. Damit erhalten wir
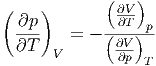 | (2.9) |
Mit der Definition der isothermen Kompressibilität
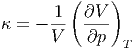 | (2.10) |
lautet Gleichung (2.9)
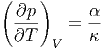 | (2.11) |
Damit erhält Gleichung (2.7) die Form
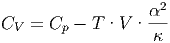 | (2.12) |
Traditioneller ist die Schreibweise
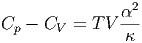 | (2.13) |
Gleichung (2.13) gilt für beliebige Substanzen. Bei der Herleitung wurden ausser dem ersten Hauptsatz, der implizit in den Maxwellschen Relationen steckt, keine Annahmen gemacht.
Für molare Wärmekapazitäten erhalten wir die Beziehung
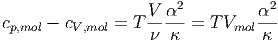 | (2.14) |
wobei ν die Molzahl ist.
Die spezifischen Wärmekapazitäten cy = Cy∕V hängen wie folgt zusammen:
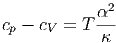 | (2.15) |
Beispiel:
Für Kupfer erhalten wir die folgenden Beziehungen
| V mol | = 7.1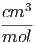 = = 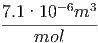 | ||
| α | = 5·10-5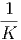 | ||
| κ | = 4.5·10-13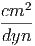 = 4.5·10-13· = 4.5·10-13·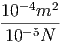 = 4.5·10-12 = 4.5·10-12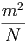 | ||
| cp,mol | = 24.5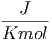 |
| cp,mol - cV ,mol | = 1.2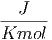 | ||
| γ | = 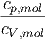 = 1.05 = 1.05 |
Hier wollen wir untersuchen, wie CV sich mit dem Volumen ändert. Die Wärmekapazität
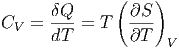 |
hängt von der Entropie ab. Wir nehmen an, dass die Entropie eine Funktion der Temperatur und des Volumens sei.
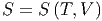 |
Dann lautet das totale Differential
| dS | = 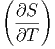 V dT + V dT + 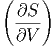 T dV T dV | ||
= 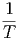 CV dT + CV dT + 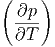 V dV V dV | (2.16) |
Die Volumenableitung der Wärmekapazität ist
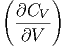 T T | = 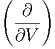 T T ![[ ( ∂S ) ]
T ---
∂T V](td-2015985x.png) | ||
= T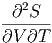 | |||
= T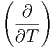 V V 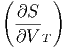 | |||
= T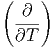 V V 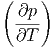 V V | (2.17) |
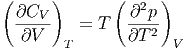 | (2.18) |
Mit der Zustandsgleichung für das ideale Gas p = NkT∕V erhält man
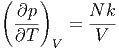 |
und
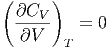 |
Die Wärmekapazität des idealen gases hängt also nicht vom Volumen ab. Dies ist einsichtig: es gibt keine Wechselwirkung zwischen den Teilchen, also darf die mittlere Distanz zwischen ihnen, gegeben durch das Volumen, keinen Einfluss haben!
Hier möchten wir wissen, wie die innere Energie U(T,V ) von der Temperatur und dem Volumen abhängt? Wir verwenden Gleichung (2.16) und erhalten
| dU | = TdS - pdV | ||
= 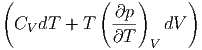 - pdV - pdV | |||
= 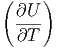 V dT + V dT + 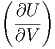 T dV T dV | (2.19) |
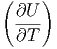 V V | = CV | (2.20) |
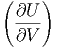 T T | = T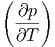 V - p V - p | (2.21) |
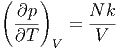 |
einsetzen, erhalten wir
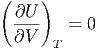 |
 Lizenzinformationen
Lizenzinformationen