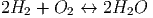

Beispiel:
Die Knallgasreaktion wird so beschrieben
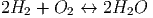 |
Dabei ist die nach rechts laufende Reaktion viel wahrscheinlicher als die Umkehrreaktion. Die Standardform dieser chemischen Reaktion ist
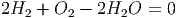 |
Allgemein werden chemische Reaktionen durch Gleichungen des Typs
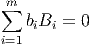 | (2.1) |
beschrieben, wobei Bi der Molekültyp und bi die Gewichtskonstante für diese Reaktion ist. Die Teilchenzahl und die Gewichtskonstante sind voneinander abhängig
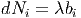 | (2.2) |
wobei λ eine Proportionsalitätskonstante ist.
Beispiel: Für die Knallgasreaktion gilt die Relation:
dNH2O : dNH2 : dNO2 = 2 : -2 : -1.
Wie immer muss die Entropie S = S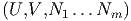 maximal werden. Das heisst: dS = 0. Wir nehmen adiabatisch
isochore Bedingungen an. Dann müssen U und V konstant
sein. Damit gilt für die Teilchenzahlen
maximal werden. Das heisst: dS = 0. Wir nehmen adiabatisch
isochore Bedingungen an. Dann müssen U und V konstant
sein. Damit gilt für die Teilchenzahlen
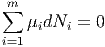 | (2.3) |
Mit Gleichung (2.2) erhalten wir
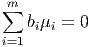 | (2.4) |
Wir betrachten die chemische Reaktion als Mischung. Die Mischungsentropie ist
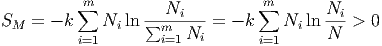 | (2.5) |
Dabei sind die Ni die Anzahl der beteiligten Moleküle der verschiedenen Spezies und N = ∑ i=1mN i die Gesamtzahl der Teilchen. Bei isobar-isothermen Reaktionsbedingungen gilt für die freie Enthalpie
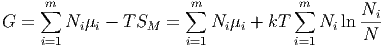 | (2.6) |
Das Gleichgewicht des Systems ist durch das Minimum von G gegeben. Durch den Term der Mischungsentropie wird keine chemische Reaktion vollständig ablaufen. Beim Knallgas zum Beispiel liegt das Gleichgewicht sehr weit bei H2O. Trotzdem verbleiben nicht reagierte Wasserstoff- und Sauerstoffmoleküle.
Zur Berechnung des Gleichgewichtes verwenden wir
| dG | = ∑
i=1m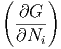 dNi dNi | (2.7) |
Eine Komponente xi = 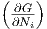 ist dann (wobei N = ∑
i=1mN
i
ist)
ist dann (wobei N = ∑
i=1mN
i
ist)
| xi | = 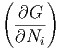 | ||
= 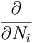 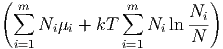 | |||
= 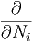 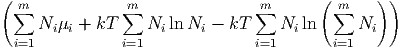 | |||
= μi + kT ln Ni + kTNi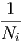 - kT ln - kT ln 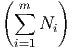 - kT ∑
j=1mN
j - kT ∑
j=1mN
j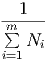 | |||
= μi + kT ln Ni + kT - kT ln N - kT ∑
j=1m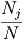 |
In jedem Summanden, ausser dem letzten, bleibt nur der Term mit Ni nach dem Ableiten übrig. Im letzten Summanden kann man für beliebige Nj nach Ni ableiten, da Ni im Logarithmus vorkommt. Damit wird
| dG | = ∑
i=1m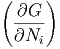 dNi dNi | ||
= ∑
i=1m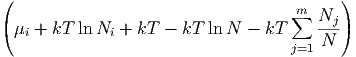 dNi dNi | |||
= ∑
i=1m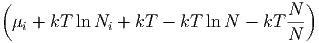 dNi dNi | |||
= ∑
i=1m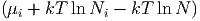 dNi dNi | (2.8) |
mit
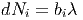 | (2.9) |
erhalten wir
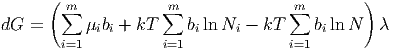 | (2.10) |
Da dG = 0 im Gleichgewicht ist, erhalten wir für λ ⇔ 0
| ∑ i=1mμ ibi + kT ∑ i=1mb i ln Ni - kT ∑ i=1mb i ln N | = 0 | ||
-∑
i=1mμ
ibi + kT ∑
i=1mb
i ln 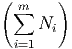 | = kT ∑ i=1mb i ln Ni | ||
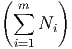 ∑
i=1mbi
exp ∑
i=1mbi
exp 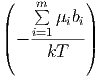 | = ∏ i=1mN ibi | (2.11) |
Bei abgeschlossenen Systemen ist die Grösse
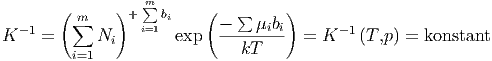 |
konstant. K heisst die Massenwirkungskonstante. Sie ist
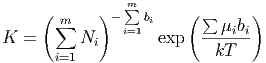 | (2.13) |
Beispiel:
Für die Knallgsreaktion gilt -2H2 -O2 + 2H2O = 0 wobei ∑ bi = 1. Daraus folgt
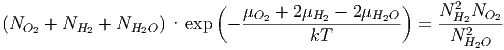 | (2.14) |
Nur wenn ∑ bi ⇔ 0 ist, ist das Reaktionsgleichgewicht unabhängig vom Druck. In allen anderen Fällen kann über den Druck p die Gleichgewichtslage der chemischen Reaktion eingestellt werden.
Wir können Gleichung (2.14) auch mit molaren Grössen schreiben
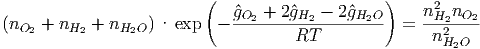 | (2.15) |
Wenn die molaren Enthalpien der Edukte (Ausgangsstoffe) gross gegen die molaren Enthalpien der Produkte sind, liegt das Gleichgewicht bei den Produkten.
Formulierung mit der Gleichgewichtskonstante K
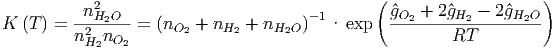 | (2.16) |
Wenn K gross ist,liegt das Gleichgewicht bei H2O.
Wenn K klein ist verschiebt sich das Gleichgewicht zu H2, O2
Aus den thermodynamischen Potentialen erhalten wir den Zusammenhang
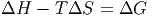 | (2.17) |
ΔH ist die freiwerdende Reaktionsenthalpie, da die Entropieänderung nicht als Wärme messbar ist. Wir haben also
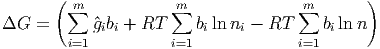 | (2.18) |
Diese Gleichung kann mit der Massenwirkungskonstante K umgeschrieben werden.
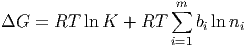 | (2.19) |
Abhängig von den ni’s kann ΔG positiv oder negativ sein. Der Standard-Wert für die freie Enthalpie pro mol wird üblicherweise mit
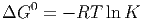 | (2.20) |
bezeichnet. Wenn wir ΔG mit den Enthalpien schreiben, bekommen wir
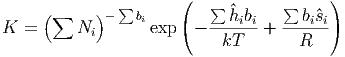 | (2.21) |
wobei ĥi die molare Enthalpie und ŝi die molare Entropie ist.
Man bekommt ΔH = ∑
ĥibi, wenn man ln K gegen 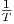 aufträgt (Arrhenius-Darstellung)
aufträgt (Arrhenius-Darstellung)
Zusammengefasst bedeutet dies
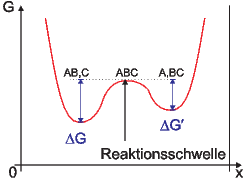
Reaktionskoordinaten
Chemische Reaktionen können mit Reaktionskoordinaten wie in der Abbildung 2.25.1 beschrieben werden. Die Ausgangssstoffe auf der linken Seite müssen dabei die Barriere ΔG überwinden, um nach rechts reagieren zu können. Umgekehrt ist die Barriere ΔG′ < ΔG. Die Anzahl Teilchen, die die Barriere überwinden können ist proportional zu
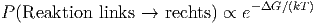 |
oder
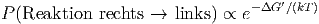 |
Im Zwischenzustand bei der Reaktionsschwelle bilden sich temporäre Gebilde, die heute mit Femtosekunden-Spektroskopie (τ = 1…10fs) zeitaufgelöst untersucht werden können.
 Lizenzinformationen
Lizenzinformationen