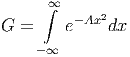

Gesucht ist
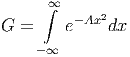 |
Dieses Integral kann in einer Dimension nicht gelöst werden. In zwei Dimensionen (x und y) können wir schreiben (Gx ist das Integral mit der Variable x geschrieben)
| Gx·Gy | = 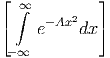 · ·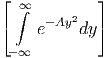 | ||
| = ∫ -∞∞∫ -∞∞e-Ax2 e-Ay2 dxdy | |||
= ∫
-∞∞∫
-∞∞e-A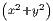 dxdy dxdy |
Wir schreiben nun Gx·Gy in Zylinderkoordinaten. Aus der Jacobi-Determinante bekommt man
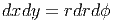 |
Also haben wir
| Gx·Gy | = ∫ 02π ∫ 0∞e-Ar2 rdrdϕ | ||
| = 2π ∫ 0∞e-Ar2 rdr |
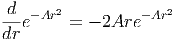 |
und damit
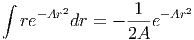 |
Wir bekommen also
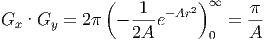 |
Schliesslich ist mit G = 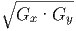
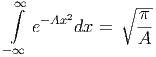 | (E.1) |
Das wichtige Integral von 0 nach unendlich hat dann den Wert
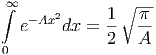 | (E.2) |
 Lizenzinformationen
Lizenzinformationen