Weiter: Energie des Magnetfeldes Oben: Zeitlich veränderliche Magnetfelder Zurück: Zeitlich veränderliche Magnetfelder Skript: PDF-Datei Übungen: Blätter
![\includegraphics[width=0.5\textwidth]{strom-017}](img1152.gif)
Induktion eines Stromes in einer in einer inhomogenen magnetischen Induktion bewegten
Leiterschlaufe.
|
Wir bewegen eine Leiterschlaufe mit der Geschwindigkeit ![]() aus dem begrenzten Gebiet mit einer homogenen
magnetischen Induktion heraus. Auf die beweglichen Ladungsträger, hier positiv angenommen, wirkt die Lorentzkraft
aus dem begrenzten Gebiet mit einer homogenen
magnetischen Induktion heraus. Auf die beweglichen Ladungsträger, hier positiv angenommen, wirkt die Lorentzkraft
![]() . Auf den horizontalen Teilen der Leiterschlaufe kennen wir den Effekt: eine
Hallspannung auf. Im vertikalen Teil im Magnetfeld bewirkt die Hallspannung eine
Beschleunigung der Ladungsträger. Nach der Definition der elektromotorischen Kraft haben
wir
. Auf den horizontalen Teilen der Leiterschlaufe kennen wir den Effekt: eine
Hallspannung auf. Im vertikalen Teil im Magnetfeld bewirkt die Hallspannung eine
Beschleunigung der Ladungsträger. Nach der Definition der elektromotorischen Kraft haben
wir
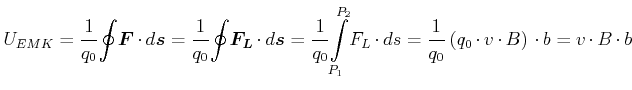 |
(4.323) |
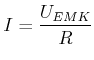 |
(4.324) |
|
|
|
|
(Siehe Leisi, Klassische Physik II [Lei98, pp. 138]) (Siehe Tipler, Physik [TM04, pp. 876])
Im Zusammenhang mit den elektrischen Feldern ![]() hatten wir den elektrischen Fluss
hatten wir den elektrischen Fluss
![]() eingeführt. Hier bewegen wir die Leiterschlaufe mit der Geschwindigkeit
eingeführt. Hier bewegen wir die Leiterschlaufe mit der Geschwindigkeit ![]() , wir
ändern damit die vom Magnetfeld durchflossene Fläche
, wir
ändern damit die vom Magnetfeld durchflossene Fläche ![]() um die Grösse
um die Grösse
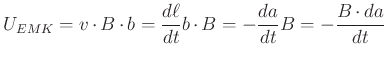 . Da die Geschwindigkeit
. Da die Geschwindigkeit
![]() ist, können wir auch schreiben
ist, können wir auch schreiben
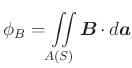 |
(4.325) |
Damit ist die induzierte EMK
Die Einheit des magnetischen Flusses ist Weber.
| (4.328) |
Das Minuszeichen in den Gleichungen für den magnetischen Fluss rührt daher, dass eine Geschwindigkeit in die
positive ![]() -Richtung eine Verkleinerung der Fläche
-Richtung eine Verkleinerung der Fläche ![]() bewirkt.
bewirkt.
Das durch den Strom erzeugte Magnetfeld ist so gerichtet, dass die Bewegung der Spule gebremst wird. Dieses Verhalten wird in der Lenzschen Regel zusammengefasst:
| Die Induktionsspannung und der Strom, den sie bewirkt, sind stets so gerichtet, dass sie der Ursache entgegenwirken. |
![\includegraphics[width=0.6\textwidth]{magnetismus-002}](img1162.gif)
Vergleich eines Stabmagneten mit einer Spule. Der magnetische Nordpol ist üblicherweise
rot, der Südpol grün markiert.
|
Eine Spule erzeugt ein axiales Magnetfeld. Die Richtung des Magnetfeldes wird mit der Rechten Hand-Regel aus der Stromrichtung abgeleitet. Ein Stabmagnet erzeugt ein gleiches Magnetfeld wie eine Spule.
|
Die Nord- und Südpole der Magnete sind so definiert: Die |
![\includegraphics[width=0.6\textwidth]{magnetismus-003}](img1163.gif)
Induzierte Spannung
|
Bewegt man einen Magneten mit der Geschwindigkeit ![]() von einem Stabmagneten weg, so bewirkt die
Lorentzkraft einen Strom
von einem Stabmagneten weg, so bewirkt die
Lorentzkraft einen Strom ![]() , der ein Magnetfeld
, der ein Magnetfeld
![]() induziert. Dieses Magnetfeld ist so
gerichtet, dass es gleichsinnig wie das Magnetfeld des Stabes ist. Der Metallring wird also vom Stabmagneten
angezogen und in seiner Bewegung nach rechts gebremst (Lenzsche Regel).
induziert. Dieses Magnetfeld ist so
gerichtet, dass es gleichsinnig wie das Magnetfeld des Stabes ist. Der Metallring wird also vom Stabmagneten
angezogen und in seiner Bewegung nach rechts gebremst (Lenzsche Regel).
![\includegraphics[width=0.9\textwidth]{magnetismus-001}](img1165.gif)
Vorzeichen des Magnetfeldes und der induzierten Spannung beim Ein- und Ausschalten.
|
Hier wird ein Magnetfeld eingeschaltet. Die Richtung der Feldlinien wird durch die Rechte-Hand-Regel bestimmt. Ein zeitlich zunehmendes Magnetfeld in der rechten Spule ist äquivalent zu einer Bewegung der rechten Spule im inhomogenen Feld (links intensiver als rechts) nach links. Dabei zeigt die relevante Feldkomponente nach aussen. Aus der Rechten Hand-Regel ergibt sich die angegebene Stromrichtung. Nach dem Ausschalten des erregenden Stromes nimmt die Intensität des Magnetfeldes ab. Dies ist äquivalent zu einer Bewegung der rechten Spule nach rechts, bei gleichbleibender Richtung des Magnetfeldes. Entsprechend dreht sich die Richtung des Stromes um.
![\includegraphics[width=0.3\textwidth]{magnetismus-004}](img1166.gif)
|
Wenn eine Spule von einem Strom durchflossen ist, wird dadurch ein Magnetfeld erzeugt. Wenn nun der Strom durch die Spule geändert wird, wird eine Spannung induziert, die wie im vorigen Falle so gerichtet ist, dass sie der Änderung des Magnetfeldes entgegenwirkt, so also auch der Änderung des durch die Spule fliessenden Stromes. Im besonderen Falle, dass der Strom abgeschaltet wird, dass also der Widerstand im Stromkreis um viele Grössenordnungen steigt, bildet sich eine sehr hohe Spannung.
Anwendungen
|
|
Wir betrachten die Situation in der Abbildung 4.1 im Ruhesystem ![]() der Schleife. Im Laborsystem
der Schleife. Im Laborsystem
![]() ist das Magnetfeld
ist das Magnetfeld
| (4.329) | |||
| (4.330) |
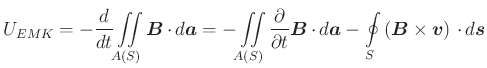 |
(4.331) |
Die Gleichungen (4.12) gelten in jedem Falle. Wenn ![]() ist, kann man die Unterschiede im
Strom
ist, kann man die Unterschiede im
Strom ![]() , in der EMK
, in der EMK ![]() und im Magnetfeld
und im Magnetfeld ![]() vernachlässigen.
vernachlässigen.
Die Transformationseigenschaften zeigen, dass das Induktionsgesetz auch bei stationären Leiterschleifen und
zeitlich ändernden Magnetfeldern gelten muss (wir begeben uns in das System ![]() ). Die Wirkungen der Felder
). Die Wirkungen der Felder
![]() und
und ![]() sind unabhängig von ihrer Entstehung.
sind unabhängig von ihrer Entstehung.
|
|
Für einen beliebig geformten ruhenden Leiter (gegeben durch die Kurve ![]() ) in einem zeitlich ändernden Magnetfeld
gilt für die EMK
) in einem zeitlich ändernden Magnetfeld
gilt für die EMK
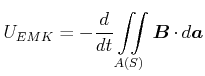 |
(4.334) |
Da der Leiter in Ruhe ist, muss die EMK durch ein elektrisches Feld erzeugt sein.
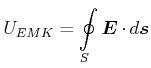 |
(4.335) |
Ist der Leiter nicht in Ruhe, dann ist mit Gleichung(C.40) und dem Satz von Stokes
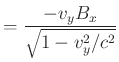 |
(4.336) |
Bei einer bewegten Leiterschlaufe ist nur die EMK relevant die im mitbewegten Bezugssystem gemessen wird. Also ist dasuniverselle Induktionsgesetz von Faraday
Mit dem Satz von Stokes erhält man
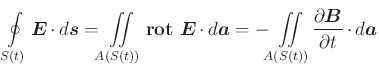 |
(4.338) |
Für zeitunabhängige Berandungen ![]() kann man auch schreiben
kann man auch schreiben
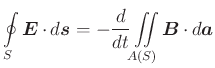 |
Da diese Integralgleichung für beliebige Kurven ![]() gelten muss, also auch für infinitesimal kleine, erhalten wir
die differentielle Form des Faradayschen Induktionsgesetzes
gelten muss, also auch für infinitesimal kleine, erhalten wir
die differentielle Form des Faradayschen Induktionsgesetzes
|
|
![\includegraphics[width=0.3\textwidth]{magnetismus-005}](img1190.gif)
|
Wenn sich ein Metallstück in einem inhomogenen Magnetfeld befindet, dann muss für jede Bahnkurve ![]() das
Faradaysche Induktionsgesetz gelten. Da der Leiter einen spezifischen Widerstand
das
Faradaysche Induktionsgesetz gelten. Da der Leiter einen spezifischen Widerstand ![]() hat, fliesst bei
einer Änderung des Flusses durch
hat, fliesst bei
einer Änderung des Flusses durch ![]() , zum Beispiel, indem man den Leiter bewegt, ein durch die induzierte Spannung
getriebener Strom. Die Richtung des Stromes ist so, dass er sich einer Änderung des magnetischen Flusses
widersetzt. Bei einem perfekten Leiter, müssten enorm grosse Kräfte aufgebracht werden, um das Metallstück mit
einer minimalen Geschwindigkeit bewegen zu können. Durch die Dissipation im Ohmschen Leiter wird der induzierte
Strom geschwächt, so dass die der Bewegung entgegengesetzte Kraft umso kleiner ist, je schlechter die
Leitfähigkeit des Metalls ist.
, zum Beispiel, indem man den Leiter bewegt, ein durch die induzierte Spannung
getriebener Strom. Die Richtung des Stromes ist so, dass er sich einer Änderung des magnetischen Flusses
widersetzt. Bei einem perfekten Leiter, müssten enorm grosse Kräfte aufgebracht werden, um das Metallstück mit
einer minimalen Geschwindigkeit bewegen zu können. Durch die Dissipation im Ohmschen Leiter wird der induzierte
Strom geschwächt, so dass die der Bewegung entgegengesetzte Kraft umso kleiner ist, je schlechter die
Leitfähigkeit des Metalls ist.
Um die Grössenordnung des Wirbelstromes abzuschätzen betrachten wir lokal ein Stück Metall das mit der
Geschwindigkeit ![]() durch eine magnetische Induktion in die
durch eine magnetische Induktion in die ![]() - Richtung,
- Richtung, ![]() , gezogen wird. Wir betrachten
die Felder im Ruhesystem der Platte. Aus den Lorentz-Transformationen erhalten wir
, gezogen wird. Wir betrachten
die Felder im Ruhesystem der Platte. Aus den Lorentz-Transformationen erhalten wir
da
![]() ist. Lokal gilt der Zusammenhang
ist. Lokal gilt der Zusammenhang
| (4.341) |
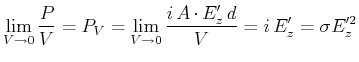 |
(4.342) |
| (4.343) |
| (4.344) |
Die Berechnung wurde anhand eines unendlich ausgedehnten Leiters in einem Magnetfeld gemacht. Endliche Leiter und endliche Magnetfelder bewirken, dass der Effekt nur an den Grenzen vorhanden ist.
![\includegraphics[width=0.7\textwidth]{magnetismus-005a}](img1205.gif)
|
Im Ruhesystem des Leiters bewirkt das elektrische Feld eine Bewegung der Ladungsträger an die Seiten des Leiters
(analog wie beim Halleffekt). Dadurch wird ein Gegenfeld aufgebaut, bis die Bewegung der Ladungsträger zum
Erliegen kommt (Siehe Abbildung 4.7, linke Seite). Wenn der Leiter den Bereich des Magnetfeldes
verlässt (wir nehmen eine scharfe Grenze an, dann gleichen sich die Ladungen aus. Die Ströme erzeugen wegen der
endlichen Leitfähigkeit ![]() eine Wärmeleistung, das heisst es gibt eine Gegenkraft. Kondensatoren werden
exponentiell entladen, so dass die Wirkung des ändernden Feldes lokal begrenzt ist. Auf der anderen Seite des
Magnetfeldes tauchen die gleichen Effekte auf, aber beim Laden des Kondensators. Auch dort nimmt der Strom
exponentiell ab beim Entfernen von der Grenze. Warum heisst es dann doch Wirbelströme? Wir haben einen Stromkreis,
bei dem die magnetische Induktion die elektromotorische Kraft bewirkt (wie beim van de Graaff-Generator). Während
im Ruhesystem des Leiters die Effekte durch das elektrische Feld erklärt werden, müssen sie im Laborsystem mit
Flussänderung und magnetischer Induktion beschrieben werden.
eine Wärmeleistung, das heisst es gibt eine Gegenkraft. Kondensatoren werden
exponentiell entladen, so dass die Wirkung des ändernden Feldes lokal begrenzt ist. Auf der anderen Seite des
Magnetfeldes tauchen die gleichen Effekte auf, aber beim Laden des Kondensators. Auch dort nimmt der Strom
exponentiell ab beim Entfernen von der Grenze. Warum heisst es dann doch Wirbelströme? Wir haben einen Stromkreis,
bei dem die magnetische Induktion die elektromotorische Kraft bewirkt (wie beim van de Graaff-Generator). Während
im Ruhesystem des Leiters die Effekte durch das elektrische Feld erklärt werden, müssen sie im Laborsystem mit
Flussänderung und magnetischer Induktion beschrieben werden.
In Transformatoren ist die magnetische Induktion parallel zum Eisen, die Wirbelströme transversal dazu. Die Wirbelströme können vermindert werden, indem das Metall geschlitzt wird oder in Lagen mit Isolatoren dazwischen gebündelt wird.
Anwendungen
Eine unendlich lange Spule kann man sich aus kreisförmigen Leitern zusammengesetzt denken.
![\includegraphics[width=0.4\textwidth]{magnetismus-006a}](img1206.gif)
Die magnetische Induktion am Punkt 0 auf der
|
Wir berechnen zuerst die magnetische Induktion eines Kreisringes mit dem Radius ![]() im Abstand
im Abstand ![]() vom Nullpunkt (
vom Nullpunkt (
![]() ) am Nullpunkt (
) am Nullpunkt (
![]() ). Ausgehend von Gleichung (3.150) schreiben wir für einen Kreisring auf der Position
). Ausgehend von Gleichung (3.150) schreiben wir für einen Kreisring auf der Position ![]() mit dem Radius
mit dem Radius
![]() für
für
![]() .
.
Da ![]() konstant ist, schreiben wir
konstant ist, schreiben wir ![]() und
und ![]() als Funktion des Winkels
als Funktion des Winkels ![]()
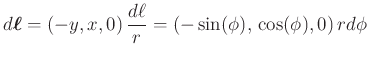
Der Strom ![]() soll im Gegenuhrzeigersinn umlaufen, also in positiver Richtung. Ein Längenelement entlang des Kreisringes ist
soll im Gegenuhrzeigersinn umlaufen, also in positiver Richtung. Ein Längenelement entlang des Kreisringes ist
Das Vektorprodukt
![]() ergibt
ergibt
Mit dem Strom pro Windung ![]() wird die magnetische Induktion am Punkte
wird die magnetische Induktion am Punkte
![]()
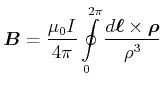 |
Die ![]() - und die
- und die ![]() -Komponenten von
-Komponenten von
![]() enthalten eine Winkelfunktion zur ersten Potenz
und ergeben bei einer Integration von 0 nach
enthalten eine Winkelfunktion zur ersten Potenz
und ergeben bei einer Integration von 0 nach ![]() null. Die
null. Die ![]() -Komponente der magnetischen Induktion ist
-Komponente der magnetischen Induktion ist
Die magnetische Induktion einer unendlich langen Spule bekommt man, indem wir den Strom ![]() durch das Produkt aus
Strom
durch das Produkt aus
Strom ![]() , der Windungszahl pro Länge (Windungsdichte)
, der Windungszahl pro Länge (Windungsdichte) ![]() und dem Längenelement
und dem Längenelement ![]() ersetzen und integrieren.
ersetzen und integrieren.
Wird die unendlich lange Spule bei ![]() geteilt, tragen beide Spulenhälften gleichviel zur magnetischen Induktion
bei
geteilt, tragen beide Spulenhälften gleichviel zur magnetischen Induktion
bei ![]() bei. Wird nun eine Hälfte entfernt, so ist die magnetische Induktion auf der Spulenachse
bei. Wird nun eine Hälfte entfernt, so ist die magnetische Induktion auf der Spulenachse
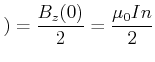 |
(4.347) |
Endlich lange Spulen der Länge
![]() verhalten sich wie unendlich lange Spulen. Wenn sich auf der Länge
verhalten sich wie unendlich lange Spulen. Wenn sich auf der Länge
![]()
![]() Windungen befinden, haben wir
Windungen befinden, haben wir
Der magnetische Fluss in einer Spule entsteht durch Ströme in dieser Spule selber, oder in anderen Spulen. Nach
dem Gesetz von Laplace oder Biot-Savart ist die magnetische Induktion
proportional zum Strom. Somit ist auch der Fluss ![]() proportional zum Strom. Diese Proportionalität wird mit
proportional zum Strom. Diese Proportionalität wird mit
| (4.349) |
Die Einheit der Induktivität ist
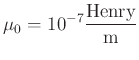
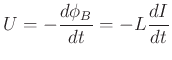 |
(4.353) |
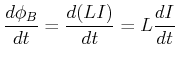 |
(4.354) |
|
|
Materialien
Folien zur Vorlesung vom 19. 06. 2008: PDF Seminar vom 19. 06. 2008. Aufgabenblatt 10 |
|
|
![\includegraphics[width=0.5\textwidth]{magnetismus-006}](img1235.gif)
Zwei gekoppelte Stromkreise
|
Der magnetische Fluss am Punkt ![]() hängt sowohl vom Strom
hängt sowohl vom Strom ![]() wie auch vom Strom
wie auch vom Strom ![]() ab:
ab:
| (4.356) |
| (4.357) |
![\includegraphics[width=0.7\textwidth]{magnetismus-007}](img1242.gif)
|
Im allgemeinen ist es schwierig, die Gegeninduktivitäten zu berechnen. Bei zwei ineinander gewickelten Spulen,
einem Beispiel für einen Transformator, gelingt dies. Wir wollen das Beispiel verwenden, um zu zeigen, dass
![]() ist. Durch die Spule
ist. Durch die Spule ![]() (Länge
(Länge ![]() , Radius
, Radius ![]() , Windungsdichte
, Windungsdichte
![]() ) fliesst der
Strom
) fliesst der
Strom ![]() , durch die zweite Spule
, durch die zweite Spule ![]() (Länge
(Länge ![]() , Radius
, Radius ![]() , Windungsdichte
, Windungsdichte
![]() ) soll der
Strom
) soll der
Strom ![]() fliessen. Da wir lange Spulen betrachten, ist das Magnetfeld im Inneren der Spulen homogen. Also ist
fliessen. Da wir lange Spulen betrachten, ist das Magnetfeld im Inneren der Spulen homogen. Also ist
| (4.358) |
| (4.359) |
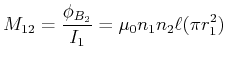 |
(4.360) |
| (4.361) |
| (4.362) |
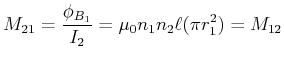 |
(4.363) |
![\includegraphics[width=0.5\textwidth]{magnetismus-008}](img1258.gif)
|
Die in einem Transformator induzierte Spannung kann wie folgt berechnet werden. In der Spule ![]() fällt die
Spannung
fällt die
Spannung
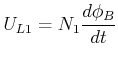 |
(4.364) |
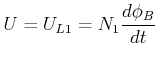 |
(4.365) |
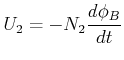 |
(4.366) |
Wird der Ausgang des Transformators mit dem Ohmschen Widerstand ![]() belastet, fliesst der Strom
belastet, fliesst der Strom ![]() , der zu
, der zu
![]() in Phase ist. Dieser Strom erzeugt einen magnetischen Fluss
in Phase ist. Dieser Strom erzeugt einen magnetischen Fluss
![]() , der den ursprünglichen
Fluss
, der den ursprünglichen
Fluss ![]() durch die Spule
durch die Spule ![]() schwächt. Da durch beide Spulen der gleiche magnetische Fluss fliesst, muss
auch der Fluss durch die erste Spule geschwächt werden. Da die Spannung durch die Spannungsquelle
schwächt. Da durch beide Spulen der gleiche magnetische Fluss fliesst, muss
auch der Fluss durch die erste Spule geschwächt werden. Da die Spannung durch die Spannungsquelle ![]() vorgegeben
ist, muss der Strom
vorgegeben
ist, muss der Strom ![]() auf der Primärseite zusätzlich fliessen, so dass
auf der Primärseite zusätzlich fliessen, so dass
![]() gilt. Da die
Proportionalitätsfaktoren bis auf das Vorzeichen gleich sind, gilt dann auch
gilt. Da die
Proportionalitätsfaktoren bis auf das Vorzeichen gleich sind, gilt dann auch
|
|
|
|
![\includegraphics[width=0.7\textwidth]{magnetismus-014}](img1269.gif)
|
In einer komplizierten elektrischen Schaltung betrachtet man eine einzelne Masche. Nach der Definition der EMK muss eine Probeladung langsam um die Masche herumgeführt werden. Dies führt auf die Maschenregel
wobei die Vorzeichen entsprechend dem Umlaufsinn einzusetzen sind. In unserem Beispiel bedeutet dies:
Die Knotenregel ist ein Ausdruck für die Ladungserhaltung. Wenn wir zum Beispiel alle zufliessenden Ströme positiv und alle wegfliessenden Ströme negativ zählen (oder umgekehrt), gilt an jedem Knoten
Mit diesen beiden Regeln sowie der Kenntnis der Charakteristika der Bauelemente kann jede statische oder quasistatische elektronische Schaltung berechnet werden.
In diesem Abschnitt betrachten wir die Wirkung von cosinusförmigen Wechselspannungen
| (4.372) |
![\includegraphics[width=0.3\textwidth]{magnetismus-009}](img1275.gif)
Definition von Strömen und Spannungen bei Wechselspannungen
|
Da bei Wechselspannungen a priori keine Stromrichtung vorgegeben ist, definiert man, zum Beispiel wie in der
Abbildung oben, die Stromrichtung zu einem bestimmten Zeitpunkt, hier für ![]() . Zu jedem Zeitpunkt muss die
Spannung im Stromkreis insgesamt null sein. Also ist
. Zu jedem Zeitpunkt muss die
Spannung im Stromkreis insgesamt null sein. Also ist
| (4.373) |
| (4.374) |
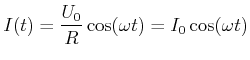 |
(4.375) |
Die momentane Leistung am Widerstand ist
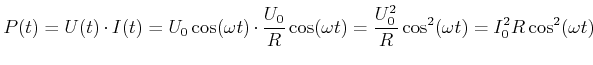 |
(4.376) |
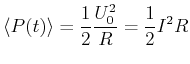 |
(4.377) |
Unter dem Effektivwert der Spannung (des Stromes) versteht man diejenige Gleichspannung, die an einem Ohmschen Widerstand die gleiche Verlustleistung erzeugt. Also ist für sinusförmige Spannungen
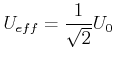 |
(4.378) |
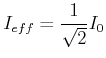 |
(4.379) |
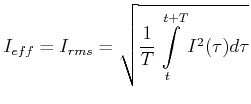 |
(4.381) |
|
|
![\includegraphics[width=0.3\textwidth]{magnetismus-010}](img1289.gif)
Spule mit Wechselspannung
|
Wir verwenden Gleichung (4.34) um die Spannung über der Spule zu berechnen. Die induzierte Spannung ist der Flussänderung entgegengesetzt. Sie wirkt so, dass die Zunahme des Stromes bei zunehmender Anregungsspannung gebremst wird. Deshalb ist
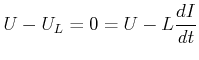 |
(4.382) |
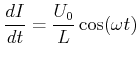 |
(4.383) |
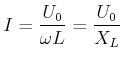 |
(4.385) |
Die momentan dissipierte Leistung an einer Spule ist
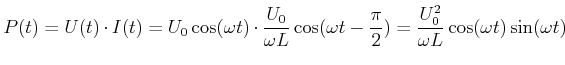 |
(4.386) |
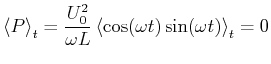 |
(4.387) |
![\includegraphics[width=0.3\textwidth]{magnetismus-011}](img1300.gif)
Kondensator mit Wechselspannung
|
Beim Kondensator ist ![]() . Diese Spannung muss gleich der treibenden Spannung sein.
. Diese Spannung muss gleich der treibenden Spannung sein.
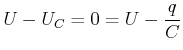 |
(4.388) |
| (4.389) |
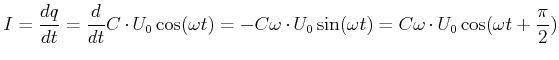 |
(4.390) |
Wir nennen
| (4.392) |
| (4.393) |
| (4.394) |
|
|
Materialien
Folien zur Vorlesung vom 23. 06. 2008: PDF |
|
|
![\includegraphics[width=0.3\textwidth]{magnetismus-012}](img1310.gif)
|
Der Kondensator soll zur Zeit ![]() auf die Spannung
auf die Spannung ![]() aufgeladen sein. Zur Zeit
aufgeladen sein. Zur Zeit ![]() wird der Schalter
geschlossen. Die Differentialgleichung dieser Schaltung lautet:
wird der Schalter
geschlossen. Die Differentialgleichung dieser Schaltung lautet:
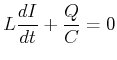 |
(4.395) |
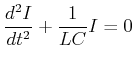 |
(4.396) |
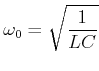 |
(4.397) |
![\includegraphics[width=0.3\textwidth]{magnetismus-013}](img1315.gif)
Schwingkreis mit Widerstand
|
Der gedämpfte Schwingkreis enthält neben dem Kondensator und der Spule auch einen Widerstand. Die Differentialgleichung des gedämpften Schwingkreises ist
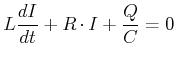 |
(4.398) |
Wenn der elektrische Schwingkreis von einer Wechselspannungsquelle getrieben wird, ergeben sich die gleichen Phänomene wie bei einem getriebenen Pendel, also auch eine Resonanz.
Anwendungen
![\includegraphics[width=0.4\textwidth]{strom-063}](img1319.gif)
![\includegraphics[width=0.4\textwidth]{strom-064}](img1320.gif)
Bestandteile eines Elektromotors. Links der Stator, rechts der Rotor mit dem Kommutator.
|
Ein Elektromotor besteht aus zwei teilen, dem Stator, der das Magnetfeld ![]() erzeugt und dem Rotor, der in diesem Magnetfeld rotiert. Die Richtung des Stromflusses im Rotor wird durch den Kommutator gesteuert.
erzeugt und dem Rotor, der in diesem Magnetfeld rotiert. Die Richtung des Stromflusses im Rotor wird durch den Kommutator gesteuert.
|
|
|
Dieses Bild zeigt einen aufgebauten Elektromotor.
|
Wir betrachten zuerst den Elektromotor als Generator. Der Fluss durch die Leiterschlaufe mit ![]() Windungen und
einer Fläche
Windungen und
einer Fläche ![]() ist
ist
| (4.400) |
| (4.401) |
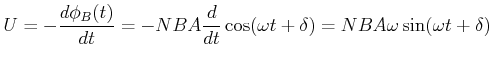 |
(4.402) |
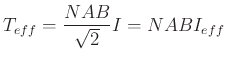 |
(4.404) |
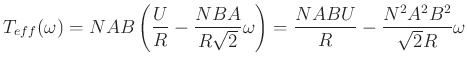 |
(4.405) |
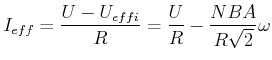 |
(4.406) |
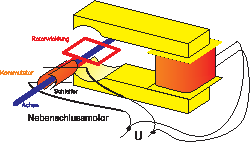 |
(4.408) |
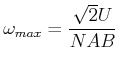 |
(4.409) |
![\includegraphics[width=0.45\textwidth]{strom-066}](img1336.gif)
Links ist die Schaltung des Nebenschlussmotors, rechts die des Hauptschlussmotors gezeigt.
|
Ist wie beim Hauptschlussmotor die Erregerwicklung in Serie zur Ankerwicklung geschaltet, gibt es keine maximale Drehzahl. Eine lange
Zylinderspule (Länge ![]() , Windungszahl
, Windungszahl ![]() ) hat das Magnetfeld
) hat das Magnetfeld
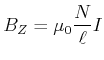 |
(4.410) |
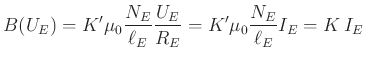 . Im statischen
Falle ist der Strom nur vom Gleichstromwiderstand
. Im statischen
Falle ist der Strom nur vom Gleichstromwiderstand | (4.411) |
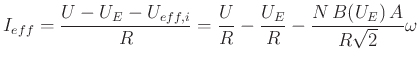 durch
durch
| (4.412) |
Da
![]() und
und
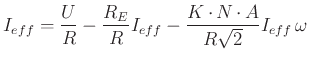 sind, gilt
sind, gilt
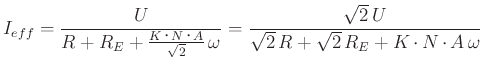 |
(4.413) |
| (4.414) |
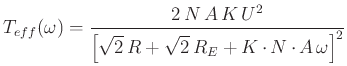 |
(4.415) |
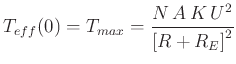 ist für alle
ist für alle ![$\displaystyle T_{eff}(0)= T_{max} = \frac{N\,A\,K\, U^2}{ \left[R+R_E\right]^2}$](img1354.gif) |
(4.417) |
|
Kennlinien von Nebenschluss- und Hauptschlussmotoren. Die Kurven wurden mit
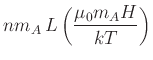 ist (eine vernünftige Annahme). ist (eine vernünftige Annahme).
|
|
|
|
|
Die Idee hinter der Konstruktion des Betatrons ist, dass bei einem zeitabhängigen ![]() -Feld nach
-Feld nach
![]() auch ein zeitabhängiges
auch ein zeitabhängiges ![]() -Feld existiert.
-Feld existiert.
![\includegraphics[width=0.7\textwidth]{magnetismus-016}](img1363.gif)
Skizze eines Betatrons
|
Nach dem Induktionsgesetz
![]() hat das durch ein in die
hat das durch ein in die ![]() -Richtung
zeigende Magnetfeld induzierte elektrische Feld keine
-Richtung
zeigende Magnetfeld induzierte elektrische Feld keine ![]() -Komponente. Nehmen wir an, dass das
-Komponente. Nehmen wir an, dass das ![]() -Feld eine
Radialkomponente hätte. Sie könnte zum Beispiel in die
-Feld eine
Radialkomponente hätte. Sie könnte zum Beispiel in die ![]() -Richtung zeigen. Rotieren wir die ganze Anordnung um
-Richtung zeigen. Rotieren wir die ganze Anordnung um
![]() um die
um die ![]() -Achse und kehren die Richtung des
-Achse und kehren die Richtung des ![]() -Feldes um, haben wir wieder die Ausgangsanordnung.
Mit der Richtungsumkehr von
-Feldes um, haben wir wieder die Ausgangsanordnung.
Mit der Richtungsumkehr von ![]() hat aber auch
hat aber auch ![]() die Richtung geändert (Induktionsgesetz). Dies ist
aber im Widerspruch zur Ausgangssituation. Deshalb kann es kein radiales
die Richtung geändert (Induktionsgesetz). Dies ist
aber im Widerspruch zur Ausgangssituation. Deshalb kann es kein radiales ![]() -Feld geben: das
-Feld geben: das ![]() -Feld
ist tangential und beschleunigt die geladenen Teilchen. Damit die Teilchen auf der Kreisbahn bleiben, muss
-Feld
ist tangential und beschleunigt die geladenen Teilchen. Damit die Teilchen auf der Kreisbahn bleiben, muss
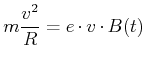 |
(4.418) |
| (4.419) |
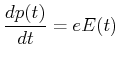 |
(4.420) |
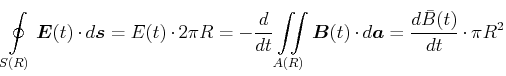 |
(4.421) |
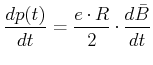 |
(4.422) |
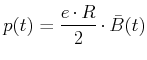 |
(4.423) |
![\includegraphics[width=0.8\textwidth]{magnetismus-017}](img1375.gif)
Berechnung des Skin-Effektes
|
Bei Gleichstrom in einem zylindrischen Leiter ist das elektrische Feld konstant über dem Querschnitt. Nach dem Ampèreschen Durchflutungsgesetz ist das Magnetfeld proportional zum Abstand.
Für den Fall eines Wechselstroms mit niedriger Frequenz müssen wir das Induktionsgesetz berücksichtigen. Nach dem
Induktionsgesetz gilt für die zeitunabhängige Kurve ![]() , die auf einer Ebene, in der auch die Zylinderachse liegt, liegt
, die auf einer Ebene, in der auch die Zylinderachse liegt, liegt
![$\displaystyle h\left[E(r)-E(r-\Delta r) \right]=\frac{d(-\bar B)}{dt}\cdot \left(-h\cdot \Delta r\right)$](img1377.gif) |
(4.426) |
![$\displaystyle \frac{\left[E(r)-E(r-\Delta r)\right]}{\Delta r}
= \frac{d(\bar B)}{dt}
$](img1380.gif)
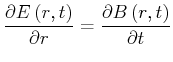 |
(4.427) |
Anwendung
Othmar Marti