| Symbol |
Name |
Einheit |
Bemerkungen |
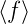 |
Mittelung über f |
− |
|
| α |
atomare Polarisierbarkeit |
|
|
| α |
Winkel (z.B. zwischen Geschwindigkeit und der Oberflächennormalen der Referenzfläche |
1 |
|
| a |
Abstand einer Ladung zur Oberfläche, Radius |
m |
|
| a |
Dicke eines Dielektrikums |
m |
|
| a |
Länge einer Leiterschlaufe in einem Motor |
m |
|
| da |
Oberflächenelement in Integralen |
m2 |
|
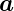 |
Beschleunigung |
|
|
| A |
Fläche |
m2 |
|
| A |
Fläche des Plattenkondensators |
m2 |
|
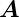 |
Vektorpotential |
Tm = |
|
| β |
reduzierte Geschwindigkeit |
1 |
β = |
| b |
Breite eines Dielektrikums |
m |
|
| b |
Breite einer Leiterschlaufe in einem Motor |
m |
|
| h |
Breite des Leiters in einer Hall-Anordnung |
m |
|
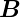 |
magnetische Induktion |
T = |
|
| c |
Lichtgeschwindigkeit im Vakuum |
|
|
| C |
Kapazität |
F = |
|
| C |
Curie-Konstante |
|
|
| cij |
Kapazität zwischen den Körpern i und j |
F |
|
| δ(t) |
Delta-Funktion für die Zeit |
|
|
| δ(x) |
Delta-Funktion für den Ort |
|
|
| δx |
Längenelement |
m |
andere Schreibweise zu dx |
| Δ |
Laplace-Operator |
|
Δf = |
d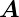 |
Flächenelement |
m2 |
|
| d |
Abstand |
m |
|
| d |
Abstand der Platten im Plattenkondensator |
m |
|
| div |
Divergenz-Operator |
|
div |
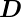 |
Dielektrische Verschiebung |
|
|
| e |
Elementarladung |
C |
e = 1.6022 × 10−19C |
| e |
Basis des natürlichen Logarithmus |
1 |
e = 2.7182818284590 |
| 𝜖 |
relative Dielektrizitätszahl |
1 |
Im Allgemeinen ist 𝜖 ein Tensor. (heisst auch relative Dielektrizitätskonstante) |
| 𝜖0 |
Dielektrizitätskonstante des Vakuums |
|
𝜖0 = 8.8544 ×
10−12 |
 ( (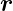 ) ) |
elektrisches Feld |
|
|
 lokal lokal |
lokales elektrisches Feld |
|
|
| E0 |
elektrisches Feld ohne Dielektrikum |
|
Verwendet bei Berechnungen mit dielektrischen Materialien |
| Epot |
potentielle Energie |
J = Nm |
|
| Et |
spezifische Haftenergie |
|
|
| ϕ |
eine der Koordinaten bei Kugelkoordinaten |
1 |
Winkel gemessen von der x-Achse in der xy-Ebene (Längengrad) |
| φ |
elektrostatisches Potential |
|
|
| φ |
Phase |
1 |
|
| Φ |
Fluss eines
Vektorfeldes |
Nm2 | |
| ΦB |
magnetischer Fluss |
1Wb =
Tm2 =
|
|
| f(x) |
Funktion |
− |
x ist ein Platzhalter |
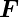 |
Kraft |
N |
|
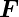 L L |
Lorentzkraft |
N |
|
| FM |
magnetische Kraft |
N |
|
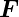 V V |
Kraftdichte |
|
|
| γ |
relativistischer Korrekturfaktor |
1 |
γ =
|
| grad |
Gradienten-Operator |
|
grad f = |
| G |
Leitwert |
S = |
|
| G |
Gravitationskonstante |
|
|
| h |
Höhe der Mantelfläche |
m |
|
| h |
Höhe des Leiters in einer Hall-Anordnung |
m |
|
| h |
Plancksches Wirkungsquantum |
Js |
h = 6.63 × 10−34Js |
| ℏ |
reduziertes Plancksches Wirkungsquantum |
Js |
h ≈ 10−34Js |
| H |
Magnetfeld |
|
|
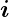 |
Stromdichte |
|
|
| I |
Strom |
A |
|
| Ieff |
effektiver Strom |
A |
|
| Irms |
RMS-Strom |
A |
Leistungsgewichteter Strom, ”Root Mean Square”-Strom |
| j |
lineare Stromdichte |
|
j =
lim Δy→0 |
| k |
Federkonstante |
|
|
| k |
beliebige, auch komplexe Zahl |
1 |
|
| kB |
Boltzmann-Konstante |
|
|
| K |
Vorfaktor |
1 |
|
| λ |
mittlere freie Weglänge |
m |
|
| λ |
Linienladungsdichte |
|
|
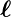 |
Abstand von −q zu +q im Dipol |
m |
|
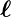 |
Drehimpuls |
|
|
| L |
Länge |
m |
|
| L |
Selbstinduktion oder Selbstinduktivität einer Spule |
H = |
|
| μ0 |
Induktionskonstante |
|
μ0 = 4π·10−7 |
| m |
Masse |
kg |
|
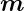 |
magnetisches Moment |
Am2 |
|
| mz |
magnetisches Moment in z-Richtung |
Am2 |
|
| M |
Gesamtmasse aller Ionen |
kg |
|
| M12 |
Gegeninduktivität zwischen zwei Spulen |
H = |
|
| MMol |
Molmasse |
|
|
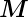 |
makroskopische Magnetisierung |
|
|
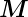 |
Drehmoment |
Nm |
|
| ν |
Frequenz |
Hz = |
|
| n |
Ladungsträgerdichte |
|
|
| n |
spezifische Windungszahl einer Spule |
|
n = |
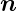 |
Normalenvektor auf ein Flächenelement |
1 |
|
| N |
Dichte der induzierten Dipole |
|
|
| N |
Windungszahl einer Spule |
1 |
|
| NA |
Avogadrozahl |
|
NA = 6.02 ×
1023 |
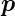 |
Dipolmoment |
Cm |
|
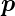 |
Impuls (mechanisch) |
|
|
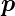 ind ind |
induziertes Dipolmoment |
Cm =
Asm =
|
|
| P |
Leistung |
W = | |
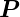 |
Polarisation |
|
|
| PM |
Leistung des Motors |
W = |
|
| q |
Ladung |
C = As =
|
|
| Q |
Ladung |
C = As =
|
andere Schreibweise für q |
| ρ |
Massedichte |
|
|
| ρel |
elektrische Ladungsdichte |
|
Siehe auch Gleichung (2.4) |
| ρ |
Ωm =
|
|
|
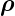 |
Abstand |
m |
|
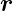 |
Abstand, Ortsvektor |
m |
|
| r0 |
Referenzradius |
m |
|
| rot |
Rotations-Operator |
|
rot |
| R |
Widerstand |
Ω = |
|
| R∗ |
Wellenwiderstand |
Ω = |
|
| R |
Radius |
m |
|
| σ |
Oberflächenladungsdichte |
|
|
| σ |
Influenzladungsdichte an der Oberfläche |
|
|
| σ |
(spezifische) Leitfähigkeit |
| |
| σMaxwell |
Maxwellspannung (mechanische Spannung) |
|
σMaxwell =
lim ΔA→0 |
| s |
Schlaufe, ein Weg |
m |
|
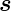 |
Spin |
Js |
|
d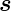 |
Längenelement |
m |
|
| S |
Bezugssystem für relativistische Rechnung |
− |
|
| S′ |
Bezugssystem für relativistische Rechnung |
− |
|
| S+ |
Bezugssystem für relativistische Rechnung |
− |
|
| S− |
Bezugssystem für relativistische Rechnung |
− |
|
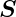 |
Poynting-Vektor |
|
|
| Θ |
eine der Koordinaten bei Kugelkoordinaten |
1 |
Winkel gemessen von der z-Achse (Breitengrad, von Norden gemessen) |
| τ |
Mittlere Zeit zwischen zwei Stössen, Relaxationszeit |
s |
|
| τ |
Abklingzeitkonstante eines RC-Gliedes |
s |
|
| τ |
Zeit unter Integralen |
s |
|
| t |
Zeit |
s |
|
| Δt |
kleine Zeitdifferenz |
s |
|
| T |
Periodendauer einer periodischen grösse |
s |
|
| T |
Temperatur |
K |
|
| U |
|
|
|
| Ugrav |
Gravitationspotential |
|
|
| UC |
Spannung am Kondensator |
V = |
|
| Ueff |
effektive Spannung |
V |
|
| Urms |
RMS-Spannung |
V |
Leistungsgewichtete Spannung, ”Root Mean Square”-Spannung |
| UEMK |
elektromotorische Kraft |
V = |
|
| UHall |
Hallspannung |
V = |
|
| UR |
V = |
|
|
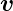 j j |
Geschwindigkeit des j-ten Ladungsträgers |
|
|
| vs |
Abziehgeschwindigkeit Klebestreifen |
|
|
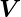 |
Hilfsvektorpotential |
Tm = |
|
| dV |
Volumenelement |
m3 |
|
| ω |
Kreisfrequenz |
|
ω = 2πν |
 |
Larmorwinkelgeschwindigkeit |
|
|
| wel |
elektrische Energiedichte |
|
|
| wB |
Energiedichte des Magnetfeldes |
|
|
| W |
Arbeit |
J = Nm |
|
| Wel |
elektrische Arbeit |
J = Nm |
|
| Wmech |
mechanische Arbeit |
J = Nm |
|
| WBatt |
Arbeit der Batterie |
J = Nm |
|
| ξ |
Ersatz für x in Integralen |
m |
|
| χe |
dielektrische Suszeptibilität |
1 | |
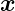 |
Ortsvektor |
m |
|
| x |
Koordinate im kartesischen Koordinatensystem |
m |
|
| XC |
Ω |
|
|
| XL |
Ω |
|
|
| y |
Koordinate im kartesischen Koordinatensystem |
m |
|
| z |
Koordinate im kartesischen Koordinatensystem |
m |
|
| Z |
Kernladungszahl |
1 |
|

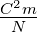
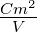
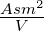
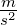
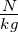
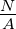
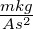
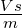

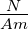
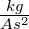
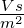
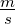
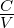
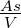
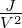
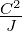
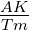
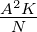
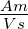
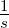
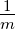
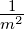
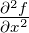
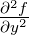
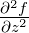
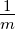
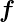
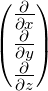
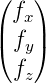
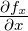
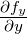
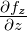
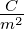
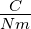
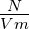
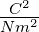
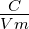
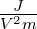
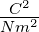
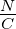
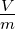
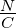
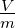
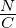
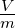
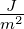
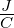
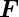
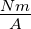
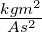
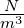
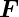
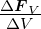
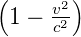
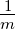
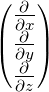
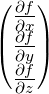
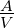
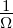
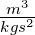
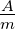
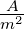
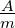
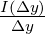
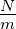
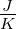
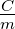
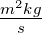
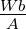
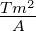
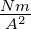
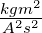
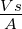
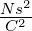
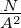
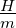
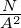
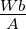
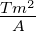
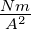
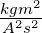
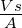
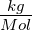
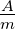
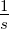
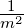
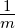
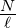
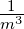
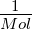
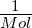
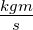
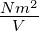
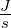
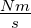
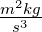
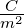
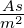
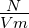
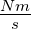
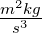
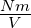
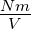
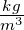
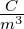
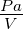
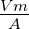
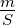
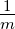
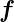
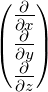
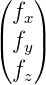
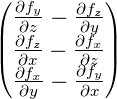
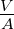
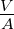
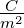
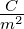
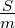
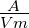
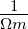
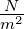
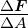
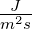
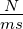
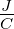
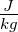
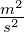
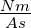
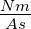
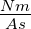
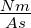
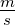
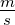
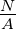
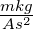
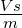
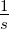
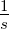
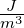
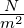
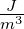
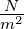
 Lizenzinformationen
Lizenzinformationen