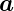 ,
, 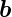 ,
, 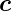 und
und 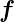 Vektoren oder vektorielle
Funktionen, a, b, c und f ihre Längen, k eine Zahl und φ(
Vektoren oder vektorielle
Funktionen, a, b, c und f ihre Längen, k eine Zahl und φ(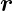 )
eine skalare Funktion. Die Komponenten der Vektoren in
kartesischen Koordinaten sind
)
eine skalare Funktion. Die Komponenten der Vektoren in
kartesischen Koordinaten sind

(Siehe Bronstein, Taschenbuch der Mathematik [BSMM08, pp. 190])
Im Folgenden sind 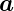 ,
, 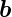 ,
, 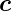 und
und 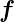 Vektoren oder vektorielle
Funktionen, a, b, c und f ihre Längen, k eine Zahl und φ(
Vektoren oder vektorielle
Funktionen, a, b, c und f ihre Längen, k eine Zahl und φ(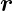 )
eine skalare Funktion. Die Komponenten der Vektoren in
kartesischen Koordinaten sind
)
eine skalare Funktion. Die Komponenten der Vektoren in
kartesischen Koordinaten sind
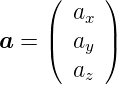
Für die anderen Vektoren werden die Komponenten analog geschrieben.
Doppeltes Vektorprodukt
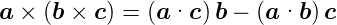 | (C.1) |
Das Spatprodukt oder gemischte Produkt berechnet das
Volumen des durch 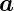 ,
,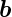 ,
,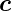 aufgespannten Spates. Das
Vorzeichen ist + bei gerader Permutation von a,b,c und −
bei ungerader Permutation.
aufgespannten Spates. Das
Vorzeichen ist + bei gerader Permutation von a,b,c und −
bei ungerader Permutation.
Drei Vektoren sind komplanar, wenn
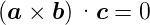 | (C.3) |
Jacobi-Identität
 | (C.4) |
Lagrangesche Identität
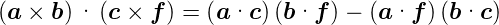 | (C.5) |
Vierfaches Vektorprodukt
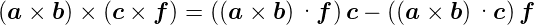 | (C.6) |
Ableiten eines Vektors
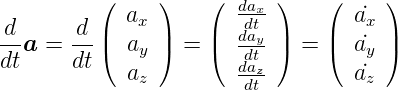 | (C.7) |
Ableitung eines Produktes
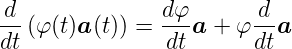 | (C.8) |
Ableitung des Skalarproduktes
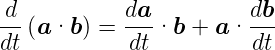 | (C.9) |
Ableitung des Vektorproduktes
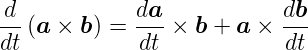 | (C.10) |
Ableitung eines Vektors mit konstantem Betrag. Hier ist
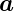 ·
·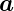 = a2 = const. Aus Gleichung (C.9) folgt
= a2 = const. Aus Gleichung (C.9) folgt
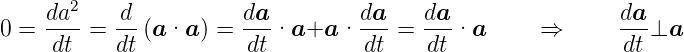 | (C.11) |
Taylorentwicklung einer Vektorfunktion
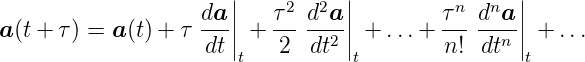 | (C.12) |
(Siehe Bronstein, Taschenbuch der Mathematik [BSMM08, pp. 668])
Ableitung eines skalaren Feldes nach einer Richtung
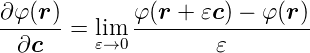 | (C.13) |
Ableitung 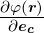 in Richtung des Einheitsvektors
in Richtung des Einheitsvektors 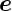
 in
Richtung von
in
Richtung von 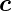
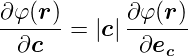 | (C.14) |
Richtungsableitung einer skalaren Funktion im Vergleich
zur Richtung mit dem stärksten Abfall (Einheitsvektor
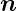 )
)
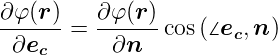 | (C.15) |
Ableitung eines Vektorfeldes 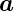 nach einer Richtung
nach einer Richtung 
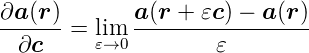 | (C.16) |
Ableitung 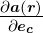 in Richtung des Einheitsvektors
in Richtung des Einheitsvektors 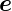
 in
Richtung von
in
Richtung von 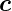
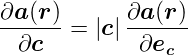 | (C.17) |
Richtungsableitung einer Vektorfunktion
Gradient eines Produktes
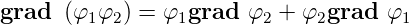 | (C.19) |
Kettenregel beim Gradienten
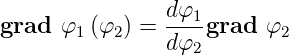 | (C.20) |
Gradient eines Skalarproduktes
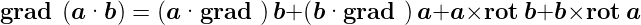 | (C.21) |
Gradient eines Skalarproduktes eines konstanten Vektors 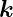 mit einem Ortsvektor
mit einem Ortsvektor 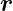
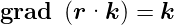 | (C.22) |
Gradient eines Vektors 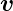 =
= 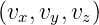 T
T
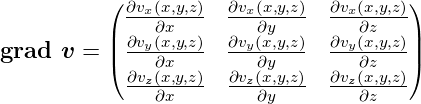 | (C.23) |
Divergenz eines Produktes
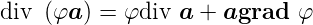 | (C.24) |
Divergenz eines Skalarproduktes eines konstanten Vektors 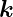 mit einem Ortsvektor
mit einem Ortsvektor 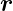
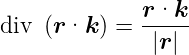 | (C.25) |
Divergenz eines Vektorproduktes
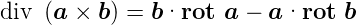 | (C.26) |
Rotation eines Produktes
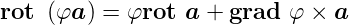 | (C.27) |
Rotation eines Vektorproduktes
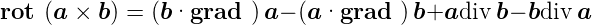 | (C.28) |
Rotation eines Potentialfeldes
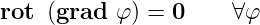 | (C.29) |
Divergenz einer Rotation
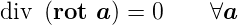 | (C.30) |
Rotation einer Rotation
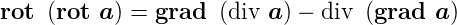 | (C.31) |
Laplace-Operator in kartesischen Koordinaten
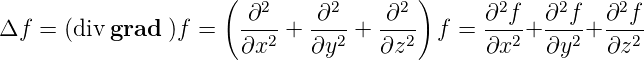 | (C.32) |
und für Vektorfunktionen
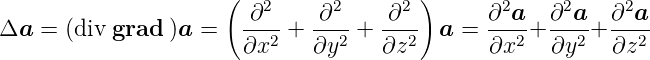 | (C.33) |
Wenn wir eine Funktion y = f(x) als Höhenprofil in einer zweidimensionalen Landschaft auffassen, dann ist
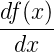
die Steigung dieses Profiles an der Stelle x. f(x) ist die Höhenangabe über einer eindimensionalen Grundfläche.
Wir können eine Funktion f(x,y) als Höhenangabe über einer zweidimensionalen Grundfläche betrachten.
__________________________________________________________________________
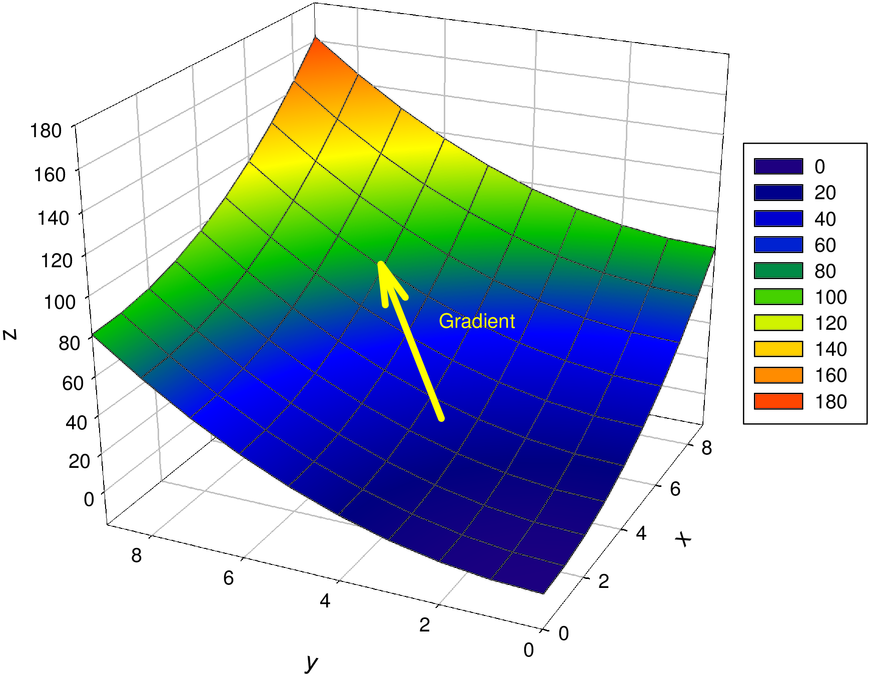
Gradient als Richtung der stärksten Steigung
_____________________________________________________________________
Die Funktion Gradient berechnet das stärkste Gefälle
einer Höhenlandschaft über einer zweidimensionalen
Ebene. Sie ist definiert:
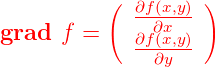
|
Eine skalare Funktion f(x,y,z) definiert eine „Höhenlandschaft“ über einer dreidimensionalen Grundfläche. Sie kann nicht mit einfachen Mitteln visualisiert werden. Hier ist die Definition
Gradient einer skalaren Funktion f(x,y,z) von drei
Variablen
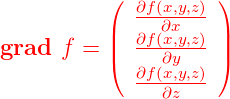
|
Wir betrachten eine Vektorfunktion
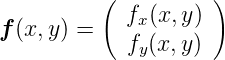
_________________________________________
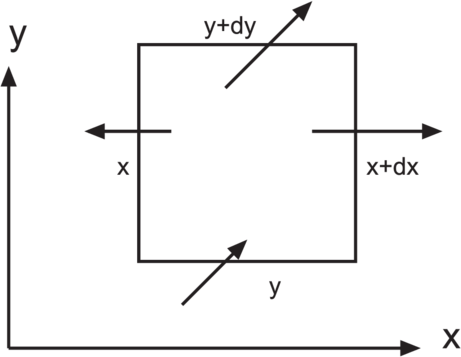
_____________________________________________________________________
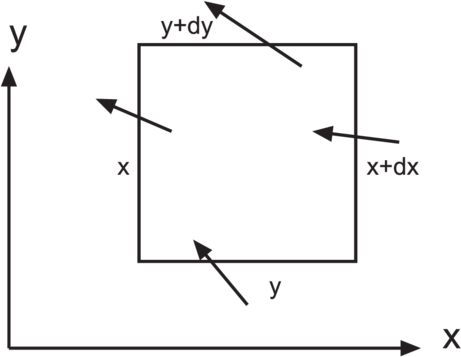
Wenn wir die Umrandung betrachten, dann sehen wir, dass netto etwas aus ihr herausfliesst. Die „Fläche“ ist dx. In die x-Richtung heisst das, dass
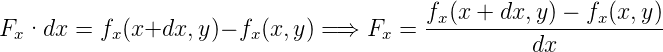
fliesst.
In die y-Richtung müssen wir die schräg liegenden Vektoren aufteilen. Die x-Komponente, fx(x,y) und fx(x,y + dy) ist parallel zur oberen und unteren Umrandung. Sie trägt nichts zum Fluss bei. Also gilt auch für die y-Richtung
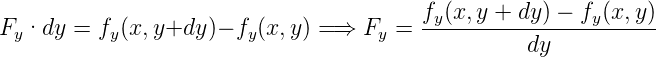
Die Grösse F = Fx + Fy nennen wir Divergenz oder Quellstärke. Mit
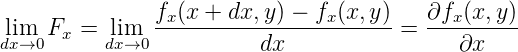
und
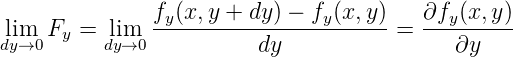
erhalten wir für die
Divergenz oder Quellstärke in 2 Dimensionen
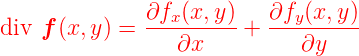
|
Eine analoge Überlegung kann man sich in drei Dimensionen machen. Die Vektorfunktion ist dann
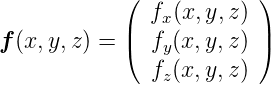
Wir definieren
Divergenz einer Vektorfunktion  (x,y,z) in drei
Dimensionen (x,y,z) in drei
Dimensionen
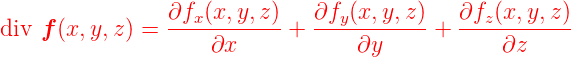
|
Wir betrachten wieder eine zweidimensionale Vektorfunktion
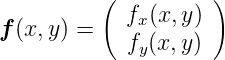
_________________________________________
Drehung eines schwimmenden Klotzes, Rotation
_____________________________________________________________________
Wir nehmen nun an, dass die durch 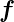 (x,y) definierten
Strömungen den rechteckigen schwimmenden Klotz beeinflussen.
So wie die Vektoren gezeichnet sind, wird er sich drehen.
Seine Drehachse zeigt aus der Zeichenebene heraus, also
die z-Richtung. Die Drehung hat etwas zu tun mit den
Grössen
(x,y) definierten
Strömungen den rechteckigen schwimmenden Klotz beeinflussen.
So wie die Vektoren gezeichnet sind, wird er sich drehen.
Seine Drehachse zeigt aus der Zeichenebene heraus, also
die z-Richtung. Die Drehung hat etwas zu tun mit den
Grössen
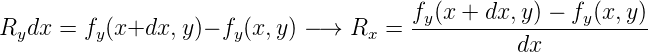
und
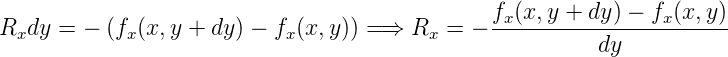
Um bei gleicher Drehrichtung (positiv ist im Gegenuhrzeigersinn) eine positive Grösse zu haben, wird bei Rx ein „−“ eingefügt. Mit
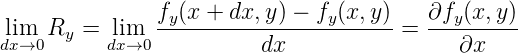
und
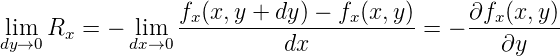
ist die Stärke der Drehung oder die
Rotation in zwei Dimensionen
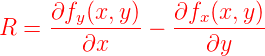
|
Diese R zeigt in die +z-Richtung, wenn wir den zweidimensionalen Raum im dreidimensionalen eingebettet betrachten. Für eine dreidimensionale Vektorfunktion
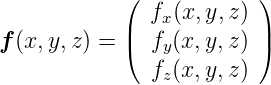
kann man sich überlegen, dass die gleichen Überlegungen wie für die xy-Ebene (Rotation um z) auch für die xz-Ebene (Rotation um y) und die yz-Ebene (Rotation um x) gelten. Wir definieren also
Rotation in drei Dimensionen
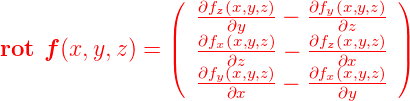
|
Man kann sich die Berechnung gut merken mit
Gedankenstütze für Rotation

|
Wenn 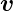 =
= 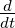
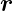 ein konstanter Geschwindigkeitsvektor ist und
diese Grösse an einem mit der Geschwindigkeit
ein konstanter Geschwindigkeitsvektor ist und
diese Grösse an einem mit der Geschwindigkeit 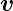 bewegten
Ort beobachtet wird, dann gilt (Siehe Jackson[Jac75,
p212]):
bewegten
Ort beobachtet wird, dann gilt (Siehe Jackson[Jac75,
p212]):
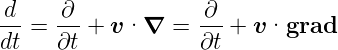 | (C.34) |
wobei 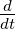 die totale Ableitung im raumfesten Koordinatensystem
und
die totale Ableitung im raumfesten Koordinatensystem
und 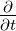 die lokale, mitgeführte Ableitung ist. Diese Gleichung
stammt von der Kettenregel:
die lokale, mitgeführte Ableitung ist. Diese Gleichung
stammt von der Kettenregel:
In drei Dimensionen muss mit dem Gradienten gerechnet werden:
Dabei bedeutet die partielle Ableitung ∂∕∂t dass man nur
nach der Zeitvariable ableitet, nicht aber nach der impliziten
Zeitableitung in 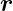 .
.
Mit Gleichung (C.28) kann man schreiben
oder
Nun ist div 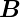 = 0. Weiter ist div
= 0. Weiter ist div 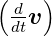 =
= 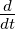 div
div 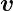 =
= 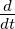 (3) = 0
und grad
(3) = 0
und grad 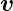 =
= 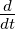 grad
grad 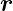 =
= 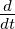 E = 0, wobei E die 3 mal
3 Einheits-Diagonalmatrix ist. Damit haben wir ohne
Einschränkung der Allgemeinheit
E = 0, wobei E die 3 mal
3 Einheits-Diagonalmatrix ist. Damit haben wir ohne
Einschränkung der Allgemeinheit
und
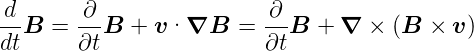 | (C.40) |
 Lizenzinformationen
Lizenzinformationen