__________________________________________________________________________
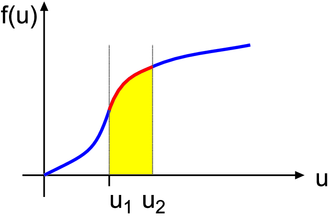
Integration einer Funktion
_____________________________________________________________________

__________________________________________________________________________

Integration einer Funktion
_____________________________________________________________________
Integrieren, d.h. Fläche unter der Kurve oder den „zurückgelegten“Weg bestimmen
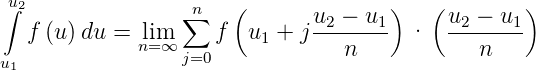 | (D.1) |
| Die verwendeten Symbole sind nebensächlich. Man kann mathematische Operationen mit allen Symbolen durchführen, z.B. die Integration mit u. |
_________________________________________________________________
| f(t) | ∫ f(τ)dτ | |
| tn | 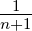 tn+1 tn+1 | wobei n ⇔ −1 |
sin 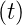 | − cos 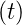 | |
cos 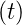 | sin 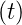 | |
| et | et | |
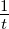 | ln(t) | |
_____________________________________________________________________
Gesetze der Integration
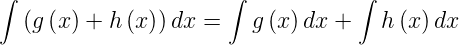 | (D.2) |
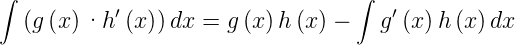 | (D.3) |
(Siehe Bronstein, Taschenbuch der Mathematik [BSMM08, pp. 447])
Konstanter Faktor
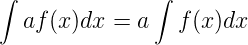
Integral einer Summe oder Differenz
![∫ ∫ ∫ ∫
[u(x) + v(x) − w(x )]dx = u(x )dx+ v(x)dx − w(x)dx](el-20172040x.png)
Substitutionsmethode
Sei y = ϕ(x)
![∫ ∫ ′
f(y)dy = f[ϕ(x)]ϕ (x)dx](el-20172041x.png)
Partielle Integration der Kettenregel der Differentiation
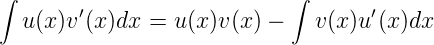
![∫ ′ ∫
f-(x) dx = df-(x)-= ln[f (x)] + C
f(x) f(x)](el-20172043x.png)
 Lizenzinformationen
Lizenzinformationen