

Up: Grundkurs IIIa 1 für Physiker
Übungsblatt 4
Grundkurs IIIa für Physiker
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
3. 6. 2002
Reflexion, Brechung, Fermatsches Prinzip,
Polarisation, Fresnelsche Formeln, Geometrische
Optik, PDF-Datei
- Ein Lichtstrahl entlang der optischen Achse (hier die x-Achse) kann an jedem
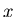 -Punkt durch den Abstand
-Punkt durch den Abstand 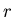 von der x-Achse und seine Steigung in dem Punkt charakterisiert werden.
von der x-Achse und seine Steigung in dem Punkt charakterisiert werden.
Wir haben also
Wenn wir die Position des Lichtstrahls an einem Punkt 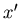 betrachten wollen, dann können wir schreiben:
betrachten wollen, dann können wir schreiben:
Die Matrix 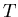 nennen wir die Transformationsmatrix.
nennen wir die Transformationsmatrix.
- Berechnen sie die Transformationsmatrix für einen ebenen metallischen Spiegel, der senkrecht zur optischen
Achse steht.
- Berechnen sie die Transformationsmatrix für Reflexion einer ebenen, senkrecht zur optischen
Achse stehenden dielektrischen Platte mit dem
Brechungsindex
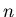 .
.
- Berechnen sie die Transformationsmatrix für Transmission einer ebenen, senkrecht zur optischen
Achse stehenden dielektrischen Platte mit dem
Brechungsindex
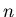 und der Dicke
und der Dicke 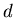 .
.
- Berechnen Sie die Transformationsmatrix für einen konkaven sphärischen Spiegel in paraxialer
Näherung.
- Berechnen Sie die Transformationsmatrix für einen konvexen sphärischen Spiegel in paraxialer
Näherung.
- Zeichnen Sie das Bild eines Objektes
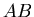 , das durch zwei Spiegel
, das durch zwei Spiegel 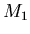 und
und 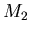 erzeugt
wird, die im Winkel von
erzeugt
wird, die im Winkel von 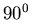 zueinander stehen. Untersuchen Sie einmal den Fall, in dem
zueinander stehen. Untersuchen Sie einmal den Fall, in dem 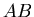 senkrecht zu der
gemeinsamen Kante ist, und einmal den Fall, in dem
senkrecht zu der
gemeinsamen Kante ist, und einmal den Fall, in dem 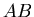 parallel zu dieser Kante ist.
parallel zu dieser Kante ist.
- Das Prisma von Porro ist ein System aus zwei totalreflektierenden Prismen, das die
unter l. beschriebene Abbildung über zwei zueinander senkrechte Richtungen realisiert. Was
macht dieses System interessant?
![\includegraphics[width=0.5\textwidth]{ue4.eps}](img13.gif)
- Der sphärische Spiegel als Autorückspiegel.
Welches sind die Eigenschaften eines sphärischen Spiegels, der von einem
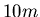 vom Scheitelpunkt entfernten
Objekt ein aufrechtes, l0-fach verkleinertes Bild erzeugt? Veranschaulichen Sie das Problem geometrisch!
vom Scheitelpunkt entfernten
Objekt ein aufrechtes, l0-fach verkleinertes Bild erzeugt? Veranschaulichen Sie das Problem geometrisch!
- Untersuchung des sphärischen Spiegels auf der Grundlage des Fermatschen Prinzips.
Geben Sie einen Ausdruck für die optische Weglänge
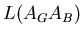 zwischen zwei konjugierten Punkten
zwischen zwei konjugierten Punkten
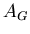 (Gegenstand) und
(Gegenstand) und 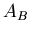 (Bild) nach
Reflexion an einem sphärischen Spiegel mit Radius
(Bild) nach
Reflexion an einem sphärischen Spiegel mit Radius 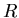 an. Leiten Sie die
Abbildungsgleichung mit Ursprung im Scheitelpunkt ab!
an. Leiten Sie die
Abbildungsgleichung mit Ursprung im Scheitelpunkt ab!
- Gesichtsfeld eines Autorückspiegels
Ein Rückspiegel besteht aus einem konvexen Spiegel, der durch einen Rand mit 4 cm Radius begrenzt ist. Seine
Brennweite hat den Absolutwert 50 cm. Das Auge befindet sich auf der optischen Achse in l m Entfernung vom
Spiegel.
Berechnen Sie den Radius 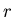 des kreisförmigen sichtbaren Teils der Ebene, die senkrecht zu der optischen
Achse und 100 m vom Spiegel entfernt ist. Vergleichen Sie dieses Gesichtsfeld mit dem eines ebenen Spiegels
mit gleichem Radius!
des kreisförmigen sichtbaren Teils der Ebene, die senkrecht zu der optischen
Achse und 100 m vom Spiegel entfernt ist. Vergleichen Sie dieses Gesichtsfeld mit dem eines ebenen Spiegels
mit gleichem Radius!
- Ein Metallspiegel ändert die Steigung, aber nicht den Abstand von der Achse
- Die Amplitude bei der Reflexion an einer dielektrischen Schicht muss mit den Fresnelschen Formeln berechnet
werden. Für die Transformationsmatrix gibt es jedoch keine Auswirkungen. Also ist
- Bei der Transmission muss das Snelliussche Gesetz in der Matrixschreibweise angegeben werden.
Es ist
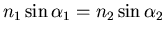 .
.
Die Steigung ist
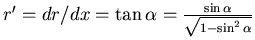
Aufgelöst nach 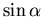 bekommt man
bekommt man
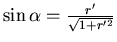
Also
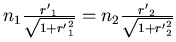
Wenn 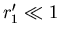 und
und 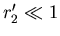 dann gilt:
dann gilt:
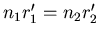
Die Matrix ist
Insgesamt bekommt man mit 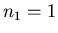
- Das Abbildungsgesetz ist
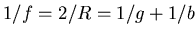
Die Steigung ist 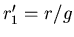 und
und 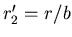
Eingesetzt bekommt man
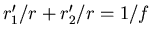 oder
oder
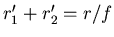
Damit auch
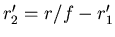
Die Matrix wird
- Das Resultat ist das gleiche wie bei der vorherigen Aufgabe, aber Vorzeichen
beachten.
-
- Die beiden Aufgaben sind in der Zeichnung gelöst:
-
![\includegraphics[width= 0.7\textwidth]{spiegel-2.eps}](img38.gif)
- Links ist die Orientierung parallel zur Kante gezeigt. Diese Orientierung ändert sich nicht.
- Rechts ist das Objekt senkrecht zur Kante orientiert. Nach der Reflexion ist das Objekt von oben nach
unten gespiegelt.
- In beiden Fällen ist das resultierende Objekt parallel zum ursprünglichen.
- Das Porro-Prisma besteht aus zwei Spiegeln nach der Aufgabe 2. Die gemeinsame Kante der
Spiegel steht senkrecht aufeinander. Deshalb werden alle Objekte um
 gedreht. Zusammen mit einem
Galilei-Fernrohr erhält man ein aufrechtes Bild. Zudem wird die optische Achse verschoben.
gedreht. Zusammen mit einem
Galilei-Fernrohr erhält man ein aufrechtes Bild. Zudem wird die optische Achse verschoben.
Anwendung: Ferngläser.
- Wir betrachten das Problem auf einer optischen Achse.
Die Abbildungsgleichung lautet
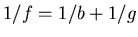
Der Abbildungsmassstab ist
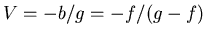
Der konvexe Spiegel muss den Gegenstand näher an das Auge bringen und soweit verkleinern, dass das
Bild nur 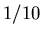 so gross ist.
so gross ist.
![\includegraphics[width=0.6\textwidth]{ue4-4.eps}](img43.gif)
![\includegraphics[width=0.4\textwidth]{ue4-4a.eps}](img44.gif)
Wenn 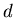 der Abstand vom Spiegel zum Auge ist,
der Abstand vom Spiegel zum Auge ist, 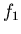 die Brennweite des Auges,
die Brennweite des Auges, 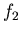 die Brennweite
des Konkavspiegels,
die Brennweite
des Konkavspiegels,  die Gegenstandsweite.
die Gegenstandsweite.
Ohne Spiegel ist die Vergrösserung
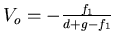
Mit Spiegel ist das Bild (= 2. Objekt) bei
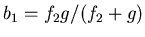 und seine Vergrösserung.
und seine Vergrösserung.
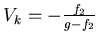 . Dieses Bild ist für das Auge der Gegenstand, mit einer Gegenstandsweite
. Dieses Bild ist für das Auge der Gegenstand, mit einer Gegenstandsweite 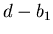 .
Also ist die Vergrösserung
.
Also ist die Vergrösserung
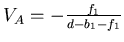
Die Gesamtvergrösserung mit Spiegel ist
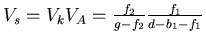 (
(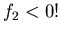 )
)
Wir setzen 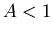 als den Vergrösserungsfaktor. Die Brennweite
als den Vergrösserungsfaktor. Die Brennweite 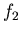 ist dann
ist dann
Wir erhalten mit 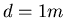 und
und 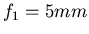
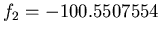 .
.
-
- Für den ebenen Spiegel mit dem Durchmesser
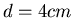 benützen wir den Strahlensatz
benützen wir den Strahlensatz
![\includegraphics[width=0.8\textwidth]{ue4-6a.eps}](img83.gif)
-
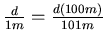 , also
, also
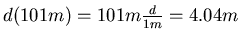
- Beim Konvexspiegel scheinen alle Strahlen vom Bildpunkt auszugehen.
- Mit
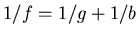 und
und 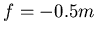 und
und 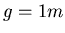 erhalten wir
erhalten wir
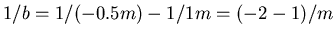 oder
oder
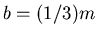
![\includegraphics[width=0.8\textwidth]{ue4-6b.eps}](img91.gif)
- Wir wenden den Strahlensatz an und erhalten
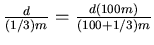 , also
, also
Übungsblatt 4
Grundkurs IIIa für Physiker
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html Uebungsblatt4
The translation was initiated by marti on 2002-06-02

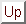

Up: Grundkurs IIIa 1 für Physiker
Othmar Marti
Experimentelle Physik
Universiät Ulm
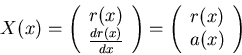
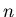 .
.
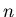 und der Dicke
und der Dicke 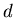 .
.
![\includegraphics[width=0.5\textwidth]{ue4.eps}](img13.gif)
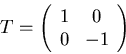
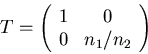
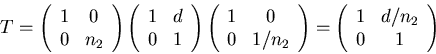
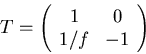
![\includegraphics[width= 0.7\textwidth]{spiegel-2.eps}](img38.gif)
![\includegraphics[width=0.6\textwidth]{ue4-4.eps}](img43.gif)
![\includegraphics[width=0.4\textwidth]{ue4-4a.eps}](img44.gif)
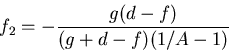
![\includegraphics[width=0.5\textwidth]{ue4-5.eps}](img60.gif)
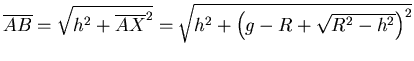
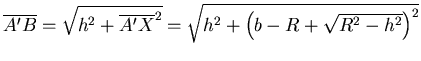
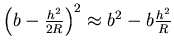
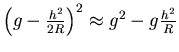
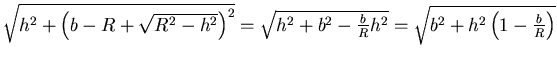
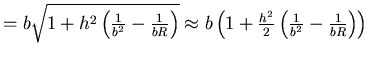
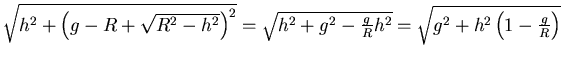
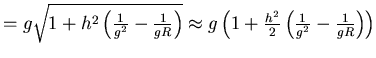
![\includegraphics[width=0.8\textwidth]{ue4-6a.eps}](img83.gif)
![\includegraphics[width=0.8\textwidth]{ue4-6b.eps}](img91.gif)