Rechnung mit Muller-Matrizen

[Nächste Seite] [Vorherige Seite] [vorheriges Seitenende] [Seitenende] [Ebene nach oben] [PDF-Datei][Epub-Datei][Andere Skripte]

A.2 Rechnung mit Müller-Matrizen

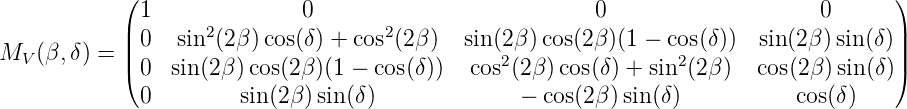
Die Rechnung mit Müller-Matrizen verläuft analog zur Rechnung mit Jones-Matrizen, nur dass über den Polarisationsgrad nichts angenommen werden muss.

Wir haben nach [Gol03] für eine Verzögerungsplatte (Phasenverzögerung δ) im Winkelβ die Müller-Matrix

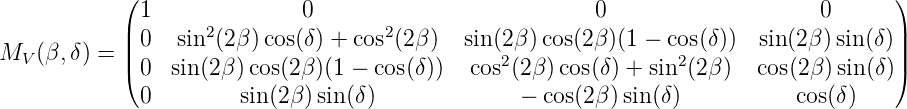( ) 1 0 0 0 ||0 sin2 (2 β)cos(δ) + cos2(2β) sin(2β) cos(2β)(1 − cos(δ)) sin(2β )sin (δ)|| MV (β, δ) = |(0 sin(2β) cos(2β)(1 − cos(δ)) cos2(2β)cos(δ) + sin2(2β) cos(2β )sin (δ)|) 0 sin (2β)sin(δ) − cos(2β) sin(δ) cos(δ)

(A.1)

Der um α gedrehte Polarisator ist durch die Müllermatrix

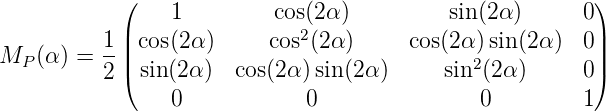( ) 1 cos(2α ) sin (2 α) 0 1-||cos(2α ) cos2(2 α) cos(2α) sin(2α ) 0|| MP (α ) = 2 |(sin(2α ) cos(2α )sin(2α) sin2(2α ) 0|) 0 0 0 1

(A.2)

gegeben. Als Eingangs-Stokes-Vektor nehmen wir

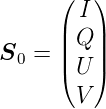( I ) | Q | S0 = || || ( U ) V

(A.3)

an. Der resultierende Stokes-Vektor 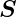₁ ist dann

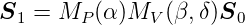S1 = MP (α )MV (β,δ)S0

(A.4)

Wir setzen δ = π∕2 (λ∕4-Platte) und bekommen

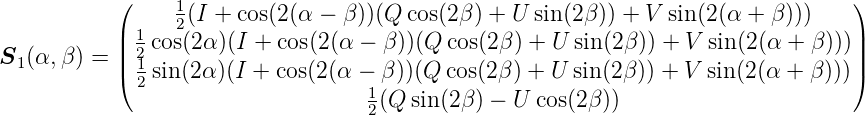( ) 12(I + cos(2 (α − β))(Q cos(2β) + U sin(2β)) + V sin (2 (α + β))) || 1cos(2α )(I + cos(2(α − β))(Q cos(2β) + U sin (2 β)) + V sin(2(α + β )))|| S1(α, β) = |( 21 |) 2 sin(2α )(I + cos(2(α −1β ))(Q cos(2 β) + U sin(2β )) + V sin(2(α + β ))) 2(Q sin(2β) − U cos(2β ))

(A.5)

Nach dem Rezept aus Abschnitt 4.4.5.2 messen wir

Die erste Komponente eines Stokes-Vektors ist die Intensität, also die Grösse, die mit einer Fotodiode, einem analogen Film oder einer sonstigen Energiemessung bestimmt werden kann. Wenn wir nun nach dem Rezept aus Abschnitt 4.4.5.2 die folgenden Summen und Diﬀerenzen bilden, erhalten wir zuerst die Stokes-Vektoren und dann die gemessenen Intensitäten

Damit ist der Stokes-Vektor und damit der Polarisationsgrad und der Polarisationszustand gemessen.

[Nächste Seite] [Vorherige Seite] [vorheriges Seitenende] [Seitenanfang] [Ebene nach oben]
©2002-2017 Ulm University, Othmar Marti, pict

Lizenzinformationen