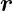 0 verschoben.
0 verschoben.

| Literatur | |
Die Beugung von Wellen an einem Objekt kann mit dem Prinzip von Fresnel-Huygens erklärt werden.
Dieses Prinzip kann mit Hilfe von sphärischen Wellen (3.8)
und der Fourier-Transformation (3.23) motiviert werden. Wir
betrachten das elektrische Feld einer elektromagnetischen Welle
in einer Ebene, praktischerweise mit z = 0. Die komplexe
Amplitude (ein Weg, die Phase mit zu berücksichtigen) ist in
dieser Ebene ortsabhängig. Der Mittelpunkt der Kugelwelle
wird dabei nach 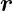 0 verschoben.
0 verschoben.
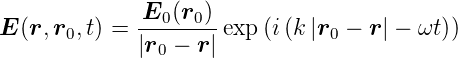 | (3.1) |
Die resultierende Welle kann als Summe von einzelwellen, oder im kontinuierlichen Falle als Integral geschrieben werden.
In Komponenten haben wir 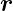 = (x,y,z)T und
= (x,y,z)T und 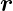 0 = (x0,y0, 0)T .
Wir setzen
0 = (x0,y0, 0)T .
Wir setzen 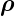 = (ρx,ρy,ρz)T = (x −x
0,y −y0,z)T . Mit der
neuen Variablen
= (ρx,ρy,ρz)T = (x −x
0,y −y0,z)T . Mit der
neuen Variablen 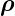 und dρx = −dx0 und dρy = −dy0 und
d
und dρx = −dx0 und dρy = −dy0 und
d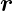 0 = (−dx0)(−dy0) = d
0 = (−dx0)(−dy0) = d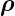 lautet das Integral:
lautet das Integral:
Weit weg von der Ebene z = 0 kann man schreiben, dass ρ ≈ρ0 ist. Wir können dann schreiben
Aus dieser Gleichung folgt, die komplexe Amplitude einer elektromagnetischen Welle, die in einer Ebene bekannt ist, näherungsweise als Fouriertransformation beschrieben werden kann. Genauere Analysen (später) sind die Kirchhoff-Theorie, die Fraunhofer-Theorie und die Fresnel-Theorie.
Andererseits kann, wenn vom Integral zurück zu einer Summe gegangen wird, und die 1∕ρ-Abhängigkeit vernachlässigt wird, das Fresnel-Huygenssche Prinzip formuliert werden.
| Das Fresnel-Huygenssche Prinzip Jeder Punkt einer bestehenden Wellenfront ist Ausgangspunkt einer neuen kugelförmigen Elementarwelle, die die gleiche Ausbreitungsgeschwindigkeit und Frequenz wie die ursprüngliche Welle hat. Die Einhüllende aller Elementarwellen ergibt die Wellenfront zu einem späteren Zeitpunkt. |
Man nimmt eine Momentaufnahme des Wellenbildes eines bestimmten Wellenberges und nimmt jeden Punkt auf diesem Wellenberg als Ausgangspunkt einer neuen Kreiswelle (Kugelwelle in 3 Dimensionen).
__________________________________________________________________________


Huygenssches Prinzip. Links die Interferenz von 5 Kreiswellen auf einer horizontalen Linie, die 4 mal so lang ist wie die Bildkante. Rechts das gleiche mit 9 Kreiswellen.
_____________________________________________________________________
_____________________________________________________________________


Huygenssches Prinzip. Links die Interferenz von 17 Kreiswellen auf einer horizontalen Linie, die 4 mal so lang ist wie die Bildkante. Rechts das gleiche mit 33 Kreiswellen.
_____________________________________________________________________
_____________________________________________________________________


Huygenssches Prinzip. Links die Interferenz von 65 Kreiswellen auf einer horizontalen Linie, die 4 mal so lang ist wie die Bildkante. Rechts das gleiche mit 129 Kreiswellen.
_____________________________________________________________________
Die Beugung an einem Spalt kann so verstanden werden, dass nicht mehr Kreiswellen aus einem grossen Bereich, sondern nur noch Kreiswellen aus dem Spalt zum neuen Wellenbild beitragen.
__________________________________________________________________________
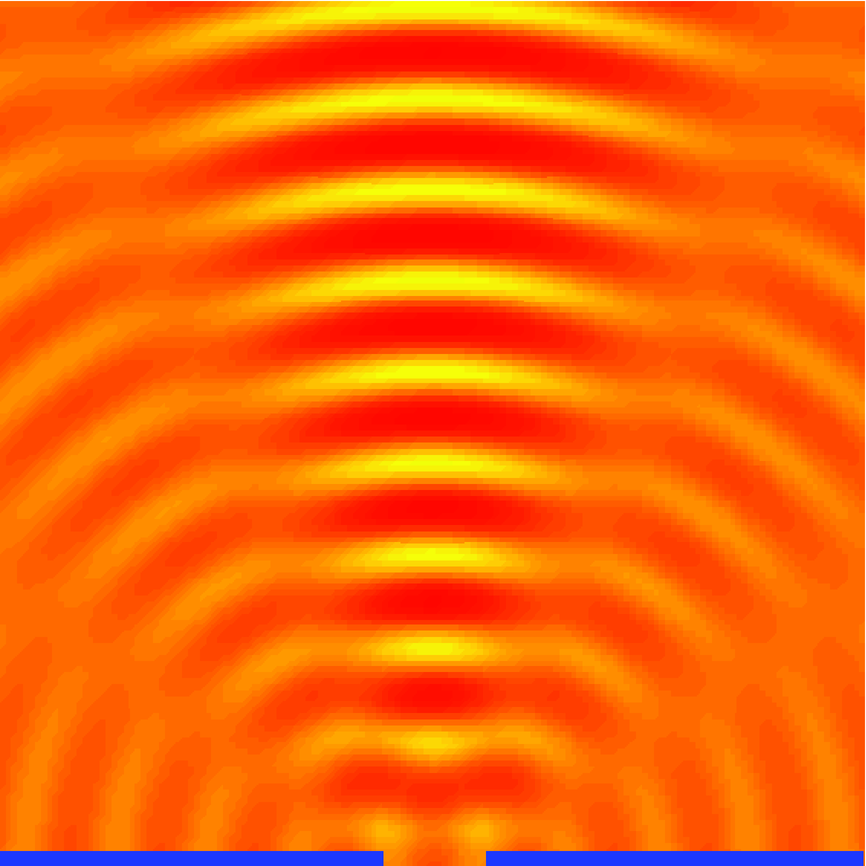
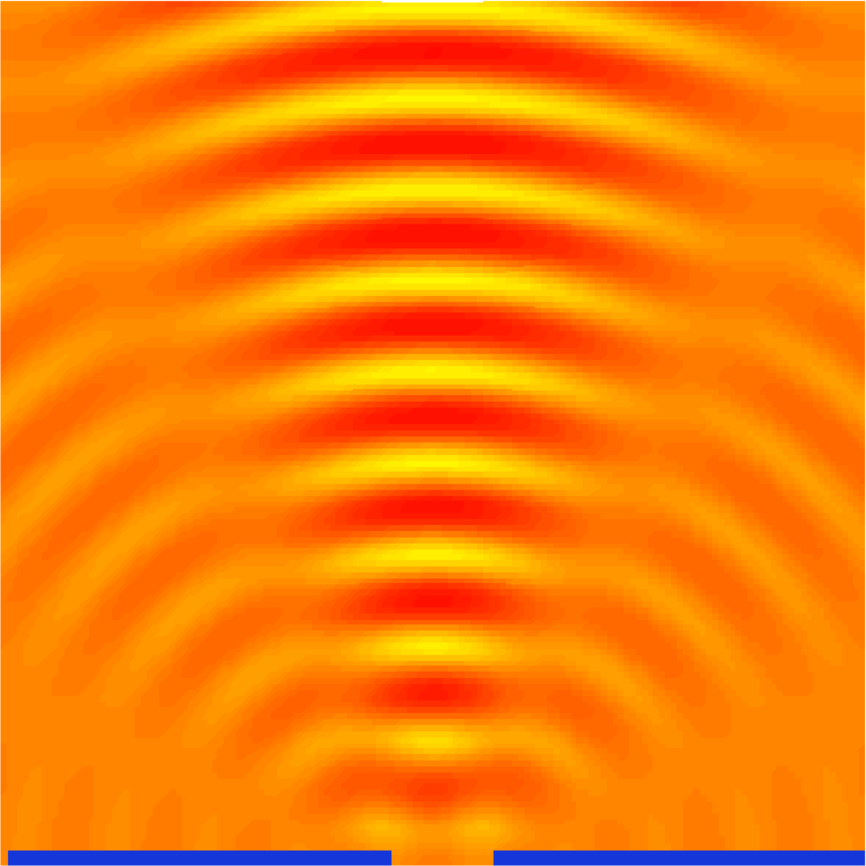
Huygenssches Prinzip. Interferenzmuster an einem Spalt. Links die Interferenz von 5 Kreiswellen auf einer horizontalen Linie im Spalt. Rechts das gleiche mit 9 Kreiswellen.
_____________________________________________________________________
_____________________________________________________________________
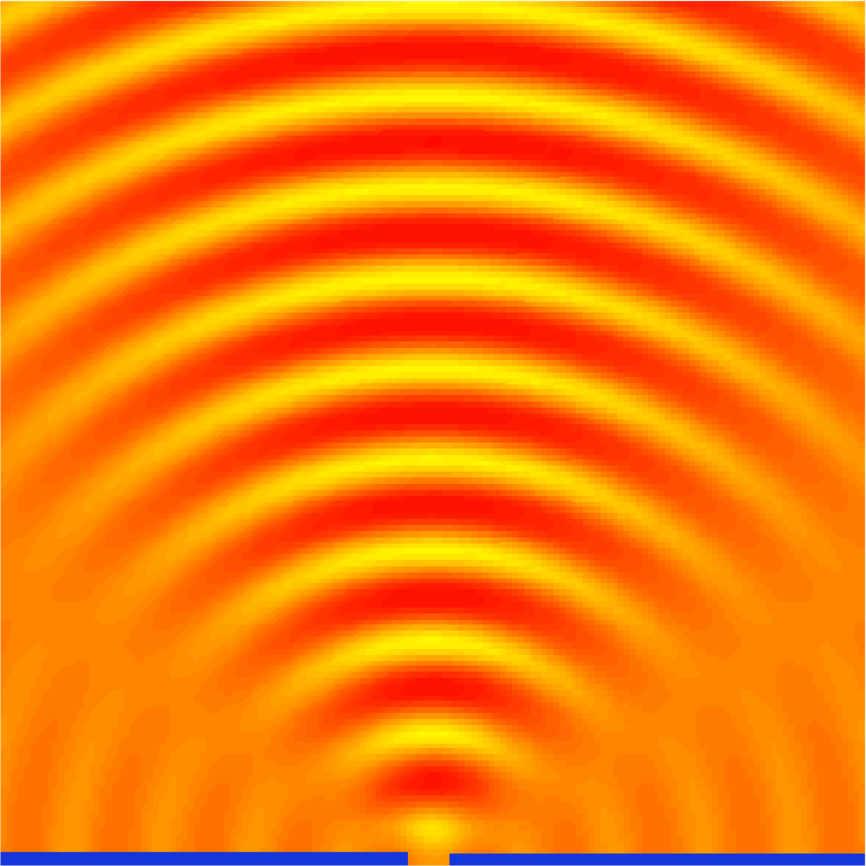
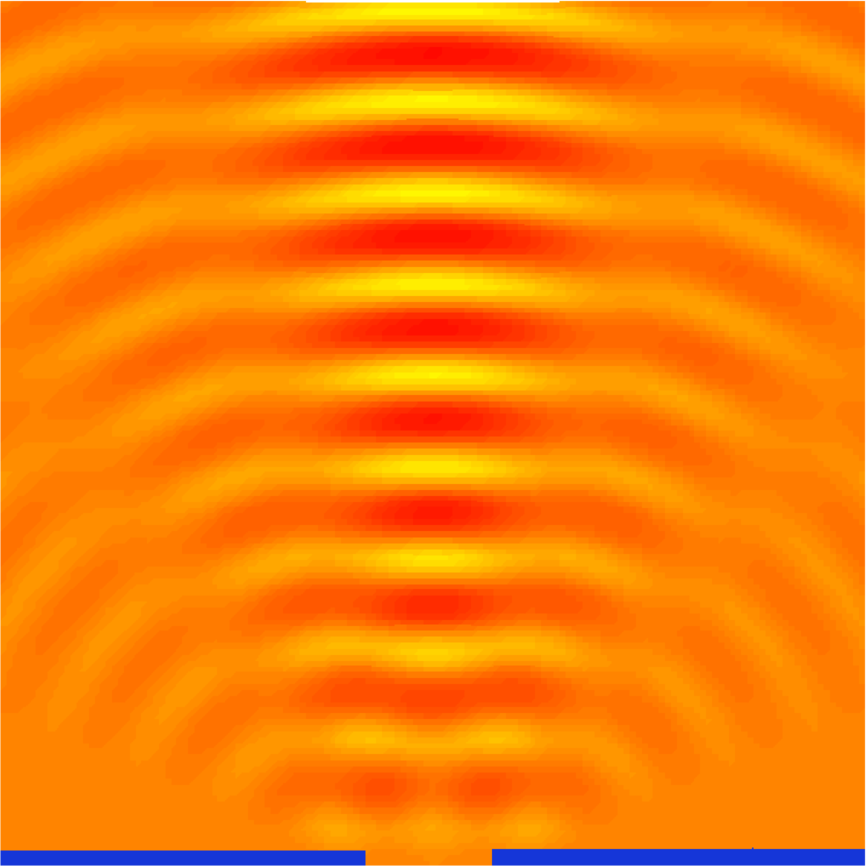
Huygenssches Prinzip. Interferenzmuster an einem Spalt. Links das Interferenzmuster bei einer Spaltbreite von 1 Wellenlänge, rechts von 3 Wellenlängen.
_____________________________________________________________________
_____________________________________________________________________
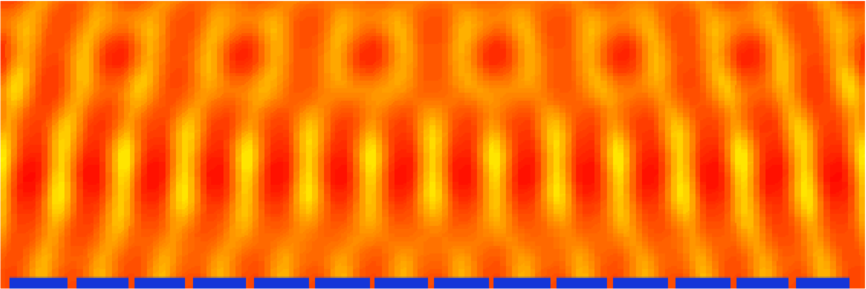
Huygenssches Prinzip. Interferenzmuster an einem Gitter. Die im Bild sichtbare Drehung rührt daher, dass nur eine endliche Anzahl von Gitterschlitzen berücksichtigt wurde.
_____________________________________________________________________
Nach dem Fresnel-Huygensschen Prinzip interferieren Kugelwellen. Bei grossem ρ (siehe auch Gleichung (3.4)) und achsnahen Positionen ist
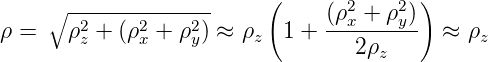 | (3.5) |
Situationen, bei denen Gleichung (3.5) gilt, heissen paraxial, die Näherung also paraxiale Näherung.
__________________________________________________________________________
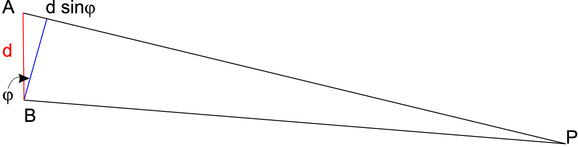
Interferenz zweier Wellen aus A und B
_______________________________________________________________
Die Interferenz von Kugelwellen kann bei etwa gleichen Amplituden nach Abbildung 3.4.1 berechnet werden. Aus der Zeichnung ist ersichtlich, dass der Weglängenunterschied von A nach P und von B nach P Δℓ = d sin φ ist. Aus Gleichung (3.1) wissen wir, dass konstruktive Interferenz auftritt, wenn
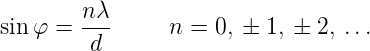 | (3.6) |
ist. In der paraxialen Näherung (kleine φ) gilt auch
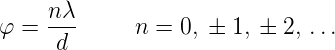 | (3.7) |
Interferenzminima treten bei
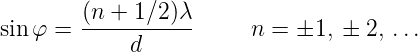 | (3.8) |
oder, in der paraxialen Näherung (kleine ϕ), bei
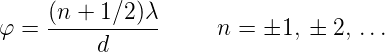 | (3.9) |
Die Lage der Interferenzextrema hängen von der Wellenlänge ab.
 Lizenzinformationen
Lizenzinformationen