©2002-2017 Ulm University, Othmar Marti, 
[Nächste
Seite] [Vorherige Seite] [vorheriges Seitenende] [Seitenende]
[Ebene nach oben] [PDF-Datei][Epub-Datei][Andere
Skripte]
4.1 Basismessverfahren
Zu den Basismessverfahren zählen die Messung von Strom
und Spannung, sowohl im Falle von Gleichstrom und
-spannung, wie auch für Wechselstrom und -spannung.
4.1.1 Strom
Ströme können sowohl mit Spannungsmessern als auch mit
Strommessern oder elektronischen Mitteln bestimmt werden.
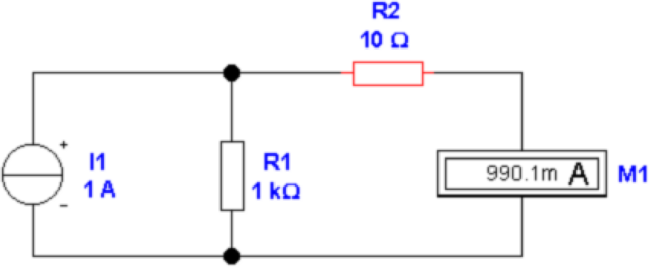
Für Gleichströme zeigt Abbildung 4.1 die Schaltung, unter
Berücksichtigung des endlichen Ausgangswiderstandes R1 der
Stromquelle und des endlichen Innenwiderstandes R2 des
Strommessers. Wenn durch Rj der Strom Ij fliesst, so gilt
für den Quellstrom IS = I1 + I2. Weiter müssen die
Spannungsabfälle an R1 und R2 gleich sein, da ja der
Strommesser ideal sein soll.
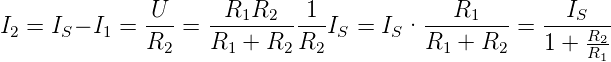 | (4.1) |
Gleichung (4.1) zeigt, dass der Messfehler umso kleiner ist,
je grösser der Ausgangswiderstand der Quelle und je kleiner
der Widerstand des Messwerkes ist. Die beiden Anordnungen
in Abbildung 4.1 unterscheiden sich im Innenwiderstand R2
des Messwerkes. Rechts ist der Innenwiderstand kleiner, der
Fehler also auch kleiner.
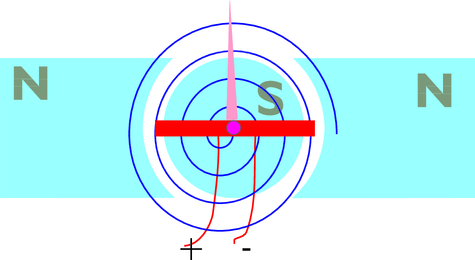
Die untere Zeile der Abbildung 4.1 zeigt den Aufbau eines
analogen Drehspulenstrommessers. Die Spule bewegt sich in
einem engen Spalt zwischen dem zylinderförmigen Südpol und
den aussen liegenden Nordpolen. Im Spalt wird, ähnlich wie
bei einem Plattenkondensator ein in guter Näherung
homogenes Magnetfeld erzeugt. Der Strom, der durch die
Spule (rot) fliesst bewirkt ein Drehmoment aufgrund der
Lorentzkraft. Die Spiralfeder erzeugt ein rückstellendes
Richtmoment, so dass das Drehmoment aufgrund des Stromes
mit dem Drehmoment der Spiralfeder verglichen wird. In
guter Näherung ist das rückstellende Drehmoment der
Spiralfeder proportional zum Auslenkungswinkel.
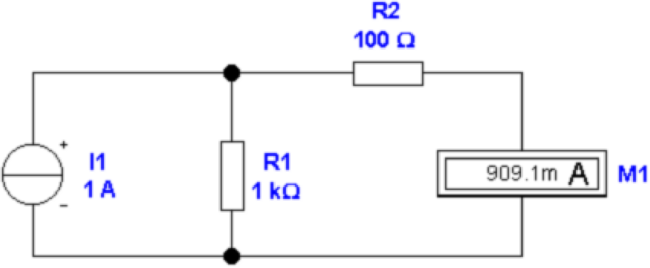
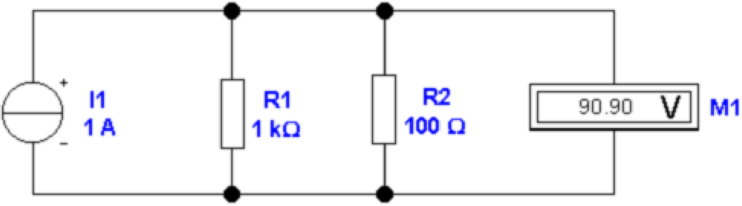
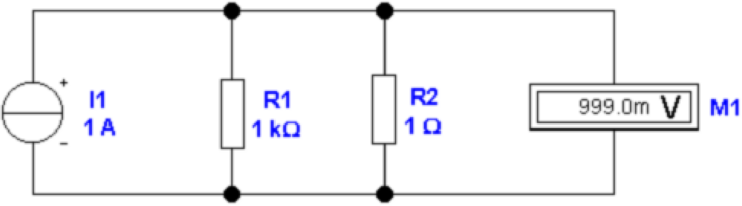
In der Abbildung 4.2 wird der Strom IS mit einem
Spannungsmesser bestimmt. Ein idealer Spannungsmesser hat
den Innenwiderstand ∞. Der Widerstand R1 ist wieder
der Ausgangswiderstand der Stromquelle. R2 ist der
Messwiderstand: er enthält, implizit, den Eingangswiderstand
des Spannungsmessers. Der Ausgangsstrom der Stromquelle
verteilt sich wieder auf die beiden Widerstände R1 und R2
nach dem Gesetz IS = I1 + I2. Gemessen wird
Wieder ist ersichtlich, dass der Fehler minimal wird, wenn
der Ausgangswiderstand R1 der Stromquelle gross gegen den
Messwiderstand R2 ist. Die beiden Darstellungen in Abb. 4.2
unterscheiden sich durch den Wert des Messwiderstandes. Aus
U2 wird mit I2 = 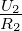 auf den Strom geschlossen.
auf den Strom geschlossen.
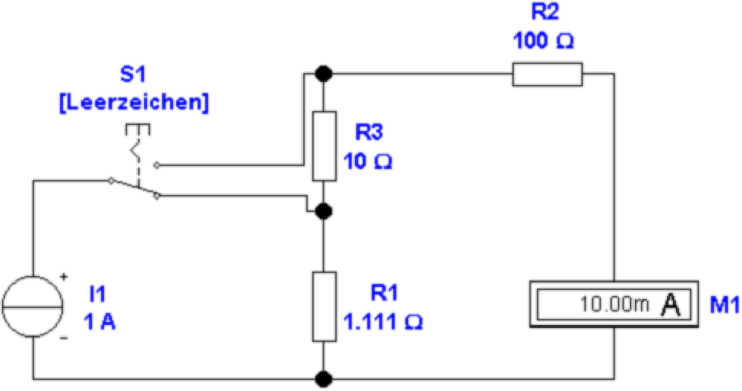
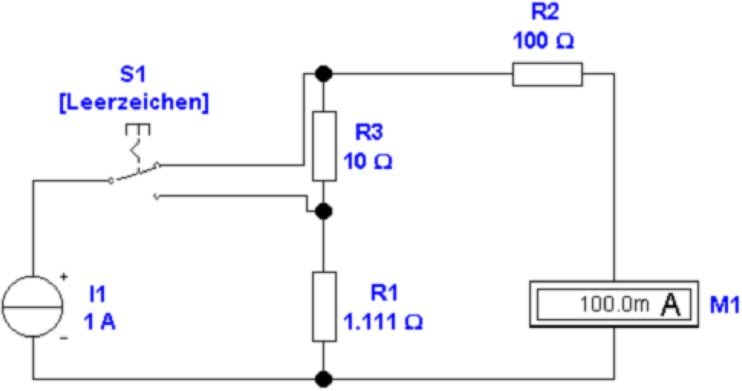
In Abb. 4.3 ist dargestellt, wie mit einer Umschaltung
Messbereiche eingestellt werden können. Hier ist R2 der
Innenwiderstand des Messwerkes. In der Abbildung 4.3 ist R3
in Serie dazu geschaltet und R1 ist der Messwiderstand. In
der Abbildung rechts ist der Messwiderstand R1 + R3, der
Innenwiderstand des Messwerkes wird allein durch R2
gebildet. Allgemein gilt für den Messstrom I2
 | (4.3) |
Mit „Alle Widerstände“ sind alle gemeint, einschliesslich
des Innenwiderstands des Messwerkes. In Abb 4.3 sind die
Werte so berechnet worden, dass links der Messstrom
ein hundertstel und rechts ein Zehntel des Quellstromes
ist.
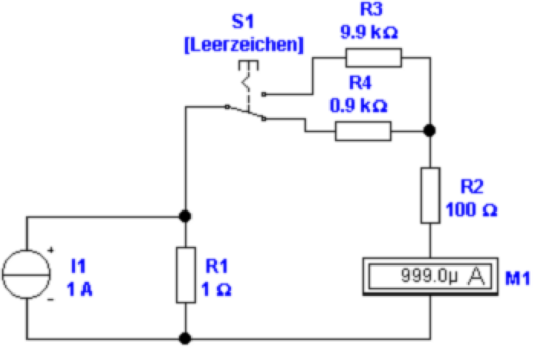
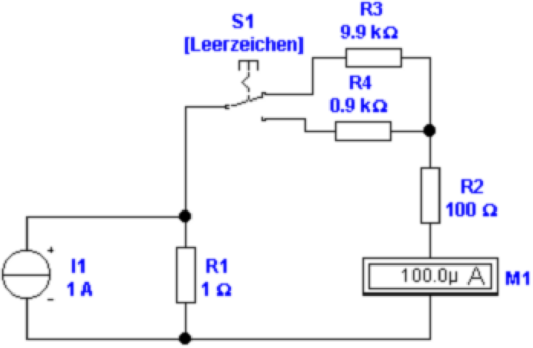
In Abb. 4.4 wird die Spannung am Messwiderstand R1 mit
einem Spannungsmesser mit umschaltbaren Bereichen
gemessen. Die Widerstände R3 und R4 werden in Serie zu R2
geschaltet. Der Quellstrom IS = I1 + I2 setzt sich aus
dem Strom I1 durch den Messwiderstand R1 und dem
Strom I2 durch das Messwerk zusammen. Es gilt für
I2
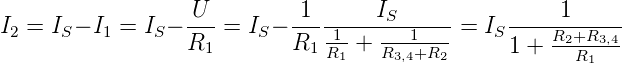 | (4.4) |
Somit ist klar, dass mit R3,4 die Empfindlichkeit umgeschaltet
werden kann. Nachteilig ist, dass der Messwiderstand
konstant bleibt, dass also die Verlustleistung P = I1R12
extrem hoch werden kann.
Die Schaltung in Abb. 4.5 ist die in der Messtechnik
gebräuchliche. R3 ist der Innenwiderstand des Spannungsmessers.
Für die gemessene Spannung U gilt:
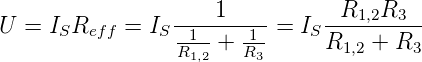 | (4.5) |
Da der Spannungsbereich fest ist, nimmt die Verlustleistung
an den Messwiderständen R1,2 nur linear zu, anders als in den
Schaltungen der Abb. 4.4.
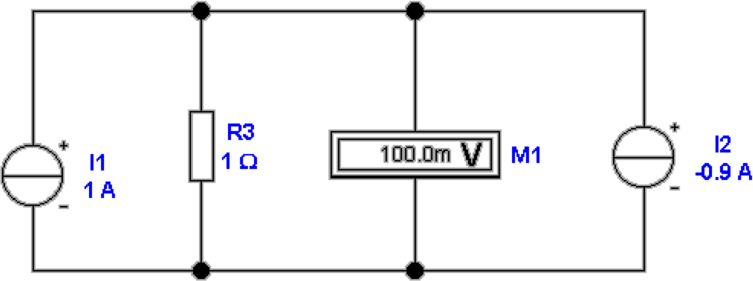
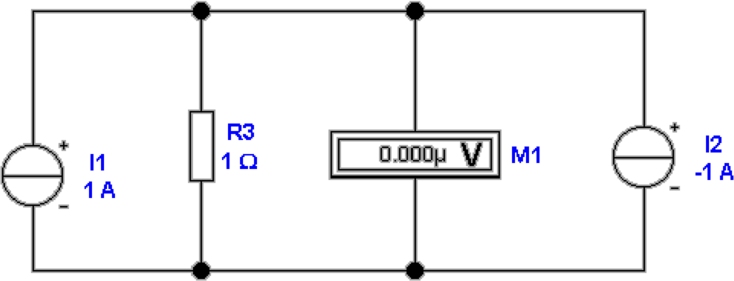
In Abb. 4.6 wird die Messung eines Stromes mit der
Kompensationsmethode dargestellt (Äquivalent zur
Poggendorffschen Spannungskompensation). Die linke Seite
der Abbildung zeigt einen nicht-abgeglichenen Zustand, die
rechte Seite ist abgeglichen.
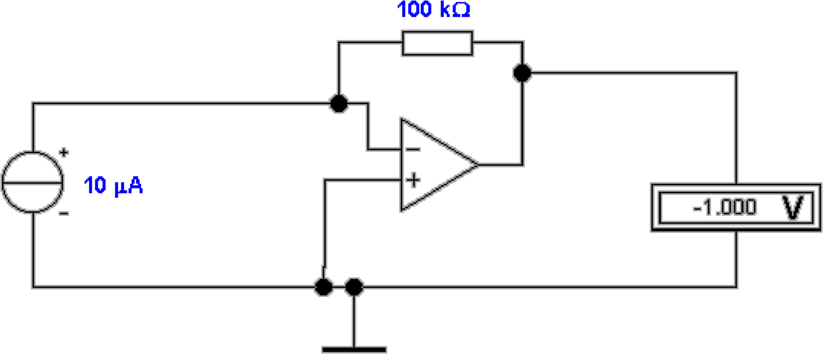
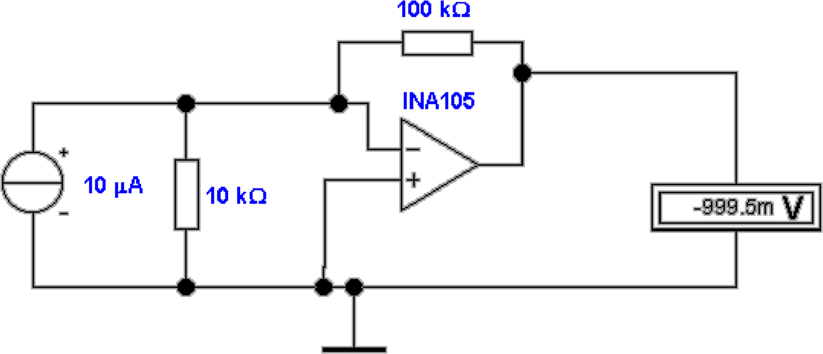
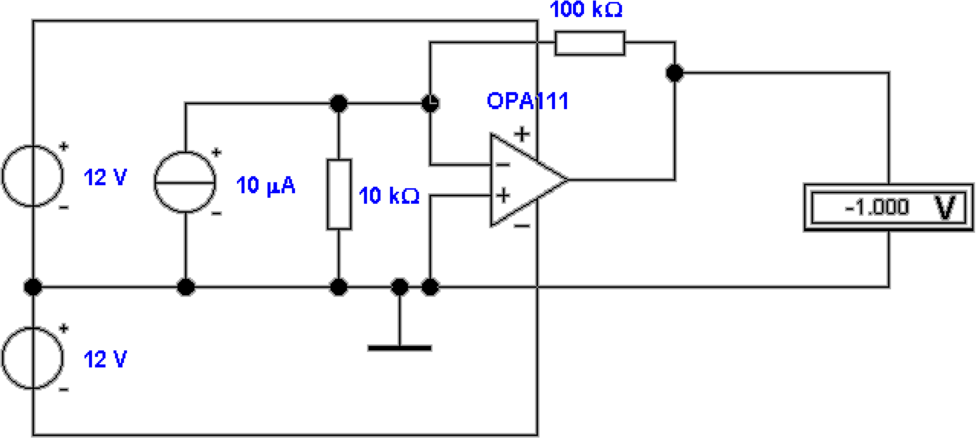
Kleine Ströme werden heute meistens mit
Strom-Spannungswandler-Schaltungen gemessen. Abb. 4.7
zeigt solche Schaltungen. Oben links ist die Schaltung
mit einem idealen Operationsverstärker aufgebaut. Es
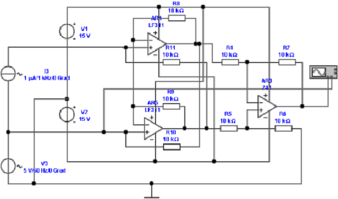
gilt:
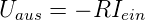 | (4.6) |
In der Abbildung ist R = 100kΩ und Iein = 10μA.
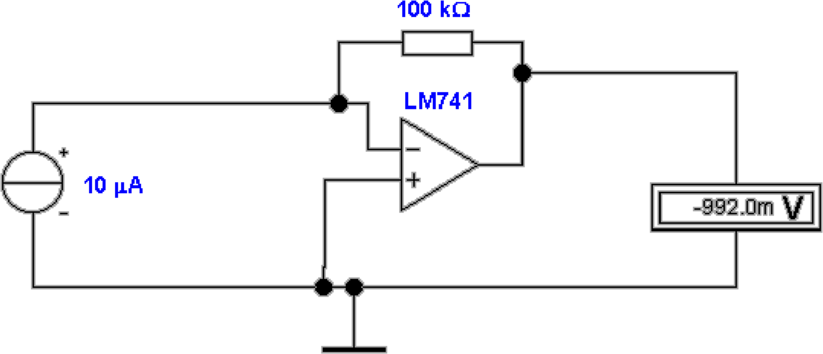
Entsprechend ist die Ausgangsspannung Uaus = 1V . Oben rechts
ist die gleiche Schaltung mit einem Operationsverstärker
LM741. Dieses Bauteil hat relativ grosse Bias-Ströme, die zu
den Eingangsströmen dazu zu zählen sind. Der resultierende
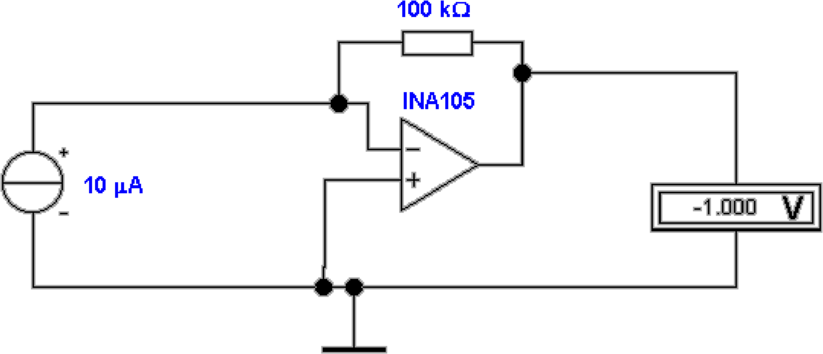
Fehler ist immerhin 0.8%. In der zweiten Reihe links ist
die Schaltung mit dem Verstärker INA105 aufgebaut.
Dieser Typ hat sehr viel kleiner Eingangsströme. Ist der
Ausgangswiderstand der Stromquelle jedoch relativ klein,
wie in der zweiten Reihe rechts gezeigt, dann ist der
Ausgang des INA105 ebenfalls fehlerbehaftet. Hier hilft, wie
unten in Abb. 4.7 gezeigt, ein Präzisionsverstärker mit
Eingangsströmen im fA-Bereich, der OPA111. Natürlich
könnte man, wie im vorangegangen Kapitel besprochen, die
BIAS-Kompensationstechniken anwenden.
Abb. 4.8 zeigt einen erdfreien Strom-Spannungswandler.
Die beiden Eingangsverstärker sind als Stromwandler
geschaltet, wobei die Rückkopplung zum jeweils anderen
Operationsverstärker geht. Die Widerstände R8 und
R9 bilden Die Rückkopplung der beiden Verstärker
AR4 und AR5. Deren invertierende Eingänge sind
zusammengeschlossen. Deshalb sind ihre beiden Ausgänge
dem Betrage nach auf der gleichen Differenzspannung, aber
mit umgekehrtem Vorzeichen. Der Rückkopplungsstrom
des einen Verstärkers wird vom Ausgang des anderen
Verstärkers aufgebracht. Deshalb ist es richtig, dass die
Strom-Spannungswandlerschaltung den nichtinvertierenden
Eingang verwendet. Diese Schaltung hat eine Verstärkung von
1 für Gleichtaktsignale. Der abschliessende Differenzverstärker
unterdrückt das Gleichtaktsignal. Hier sollte ein Typ
eingesetzt werden, der eine gute Gleichtaktunterdrückung hat.
Die Ausgangsspannung ist
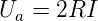 | (4.7) |
wenn die vier Widerstände der beiden Eingangsverstärker
alle gleich sind.
4.1.2 Spannung
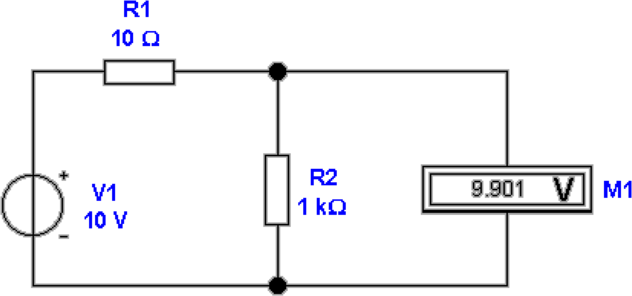
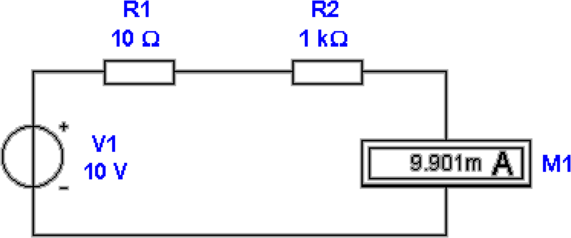
Abbildung 4.9 zeigt die Messung einer Spannung. Der
Innenwiderstand der Spannungsquelle beträgt 10 Ohm. Die
Spannung wird mit einem Innenwiderstand von einem
Kiloohm gemessen. Durch die Belastung der Spannungsquelle
mit dem Messgerät wird ein Fehler von etwa einem Prozent
erzeugt. Die gemessene Spannung ist also:
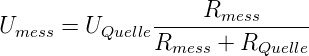 | (4.8) |
Abbildung 4.10 zeigt wieder eine Spannungsmessung,
diesmal aber mit einem Strommesser. Der Vorwiderstand des
Messgerätes ist der gleiche wie in Abbildung 4.9.Da die
Spannungsquelle den gleichen Innenwiderstand wie vorher
hat, ist Messfehler auch gleich. Man könnte ihn verringern,
indem man den vor Widerstand vergrössert. Dadurch fliesst
geringerer Strom durch das Messwerk.
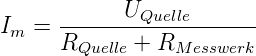 | (4.9) |
Gerade bei den analogen Messgeräten, bei denen das
Magnetfeld eine Kraft gegen eine Feder aufbringen muss, wird
ein minimaler Strom benötigt. In der Praxis ist also eine
Spannungsmessung eine Optimierungsaufgabe.
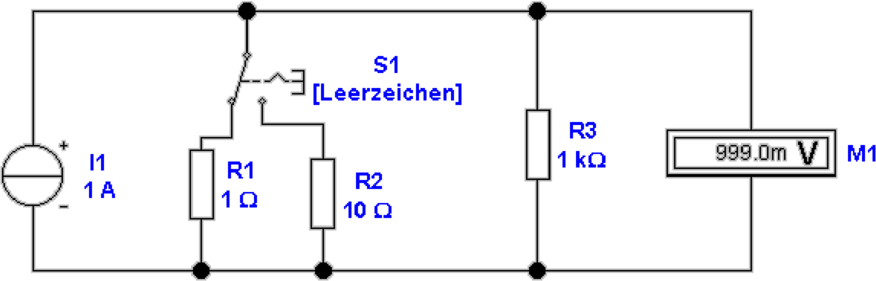
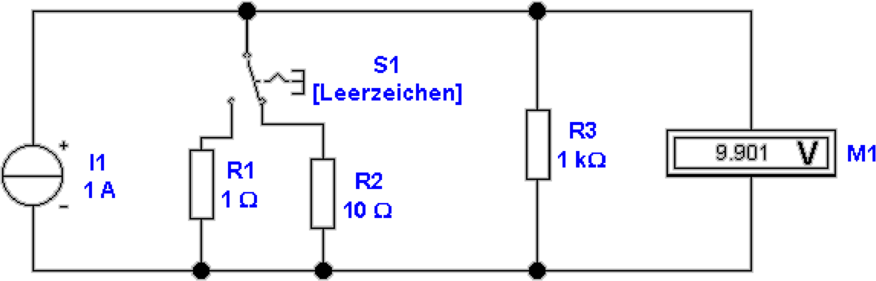
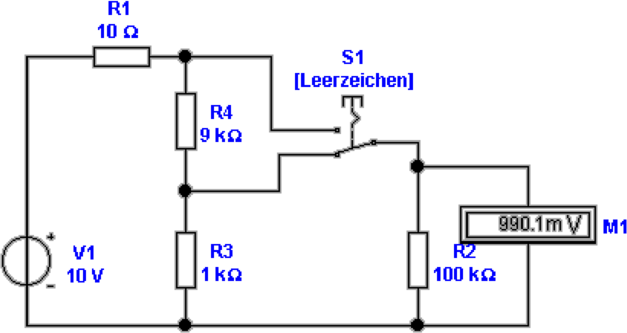
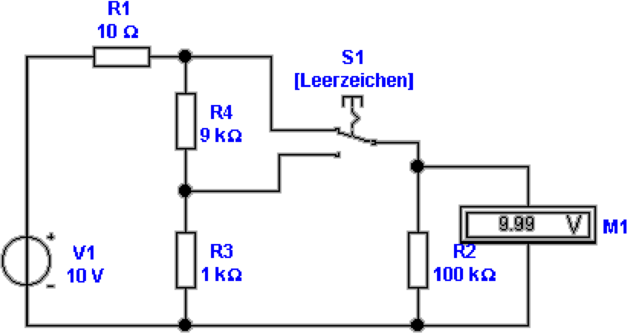
Abbildung 4.11 zeigt die Messung mit einem umschaltbaren
Spannungsmesser. Der Innenwiderstand der Quelle beträgt
wieder 10 Ohm. Eine Widerstandskette bestehend aus dem 9
Kiloohm Widerstand und dem 1 Kiloohm Widerstand
fungiert als Spannungsteiler. In unserem Fall hat das
Messgerät einen Innenwiderstand von 100 Kiloohm. Der
Innenwiderstand des Messgerätes muss gross sein gegenüber
dem Gesamtwiderstand der Spannungsteiler-Kette. Dann
ist der Messfehler vernachlässigbar. In unserem Falle
beträgt er etwa ein Promille. Die Spannungsquelle wird
mit
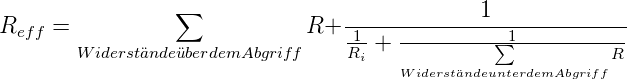 | (4.10) |
belastet. Ri ist der Innenwiderstand des Spannungsmessers.
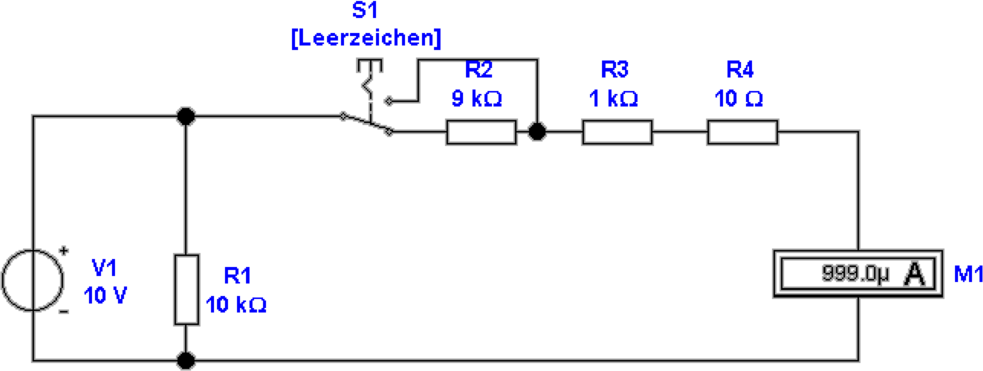
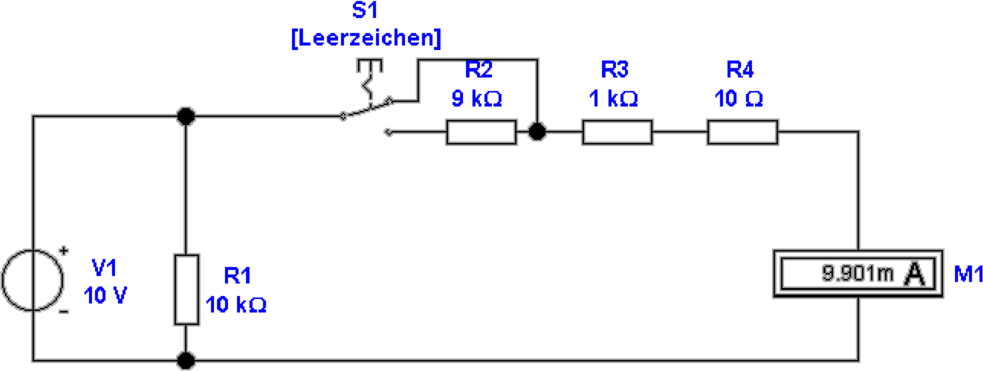
Abbildung 4.12 zeigt die Spannungsmessung mit einem
Strommesser und schaltbaren Vorwiderständen. Für den
Messstrom gilt:
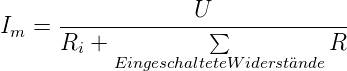 | (4.11) |
Hier ist Ri der Innenwiderstand des Strommessers und
U die angelegte Spannung. Die Spannungsquelle wird
mit
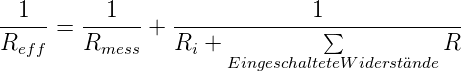 | (4.12) |
belastet. Rmess ist in Abb. 4.12 der 10 kΩ-Widerstand. Die
Schaltung ist prinzipiell gleich wie in der Abbildung 4.11.
Wieder gilt, dass der Strom durch das Messwerk genügend
gross sein muss, damit die Mechanik vernünftig ansprechen
kann.
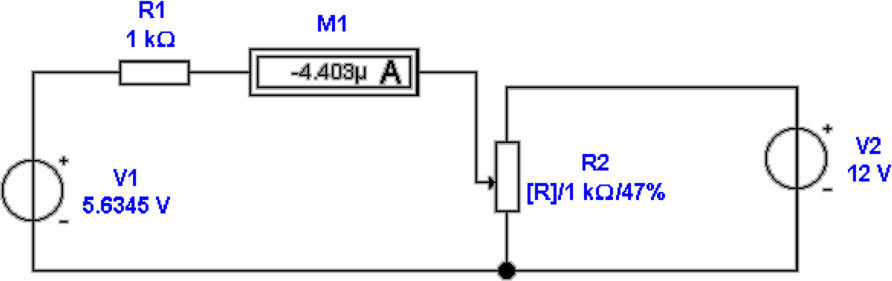
Abbildung 4.13 zeigt die Poggendorff’sche Kompensationsmethode.
Diese Methode, die auch im Praktikum angewandt wird,
vergleicht die Spannung der Quelle mit einer Referenzquelle.Die
Referenzquelle ist abstimmbar. Ihre Spannung wird so lange
verändert, bis sie gleich der der zu messenden Quelle
ist.
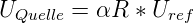 | (4.13) |
Hier ist α den Teiler, den man an R einstellt. Im
abgeglichenen Falle wird die Quelle nicht mit einem Strom
belastet. Man ist also die unbelastete Ausgangsspannung.
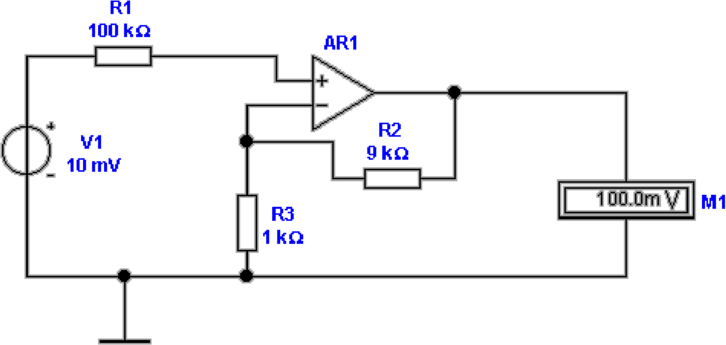
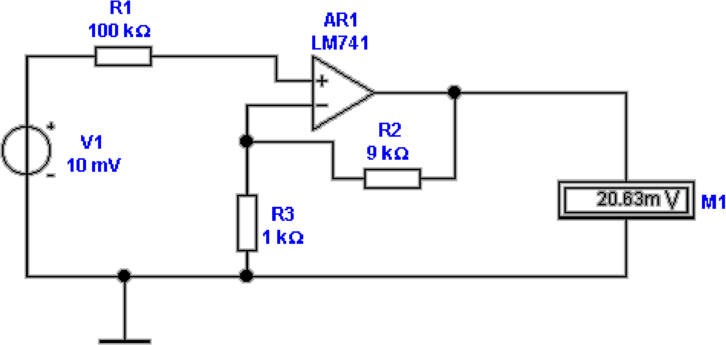
Abbildung 4.14 zeigt, wie man Spannungen mit
Operationsverstärkern messen kann. Für die Ausgangsspannung
im idealen Falle gilt:
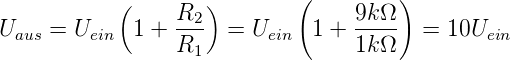 | (4.14) |
Oben links ist eine ideale Schaltung angegeben. Der
Verstärker verstärkt das Signal um den Faktor 10. Die
Spannungsquelle hat einen Innenwiderstand von 100
Kiloohm. Ihr Spannungswert von 10 mV wird durch den
Verstärker auf 100 mV erhöht. oben rechts ist die gleiche
Schaltung mit einem Verstärkern LM741 aufgebaut. Dieser
Verstärker hat relativ grosse Eingangsströme. Deshalb ist die
gemessene Spannung am Ausgang um 80 Prozent falsch.
Wenn der Strom IBias in den positiven Eingang fliesst, dann
gilt:
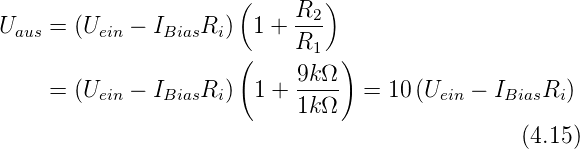
wobei RI der Innenwiderstand der Quelle ist. Hier kann
man übrigens ausrechnen, dass IBias = 0.8μA ist. Aus der
Richtung schliesst man weiter, dass die Eingangstransistoren
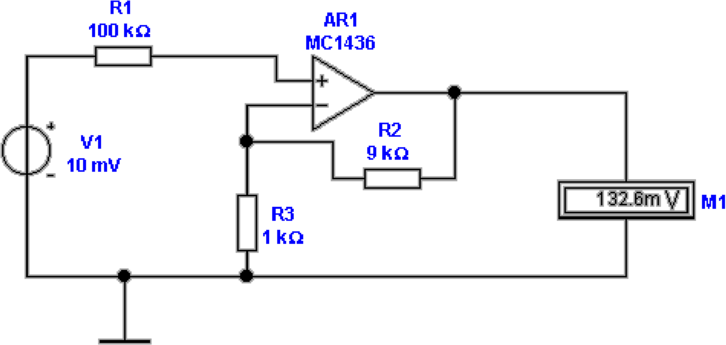
NPN-Transistoren sind. In der zweiten Zeile ist die Schaltung
mit dem Schaltkreis MC1436 aufgebaut. Bei diesem Schaltkreis
fliessen die Eingangsströme in umgekehrter Richtung. Deshalb
ist hier die gemessene Spannungen um 30 Prozent zu hoch.
Hier berechnet man, dass IBias = −0.3μA ist. Aus der
Richtung schliesst man weiter, dass die Eingangstransistoren
PNP-Transistoren sind. Unten rechts ist die Schaltung mit
dem Verstärker INA105 gezeigt. Dieser Präzisionsverstärker
hat einen Fehler von 0,5 Prozent. Es zeigt sich, dass genaue
Spannungsmessungen bei grossem Innenwiderstand der Quelle
nur mit Präzisionsverstärkern möglich ist. Geld sparen lohnt
sich hier nicht.
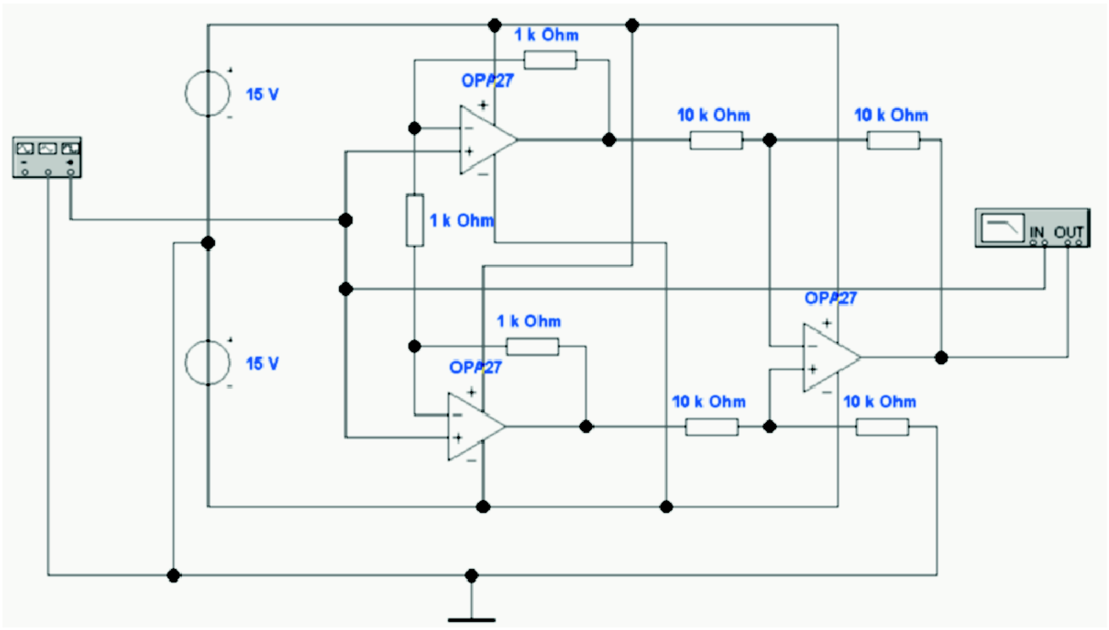
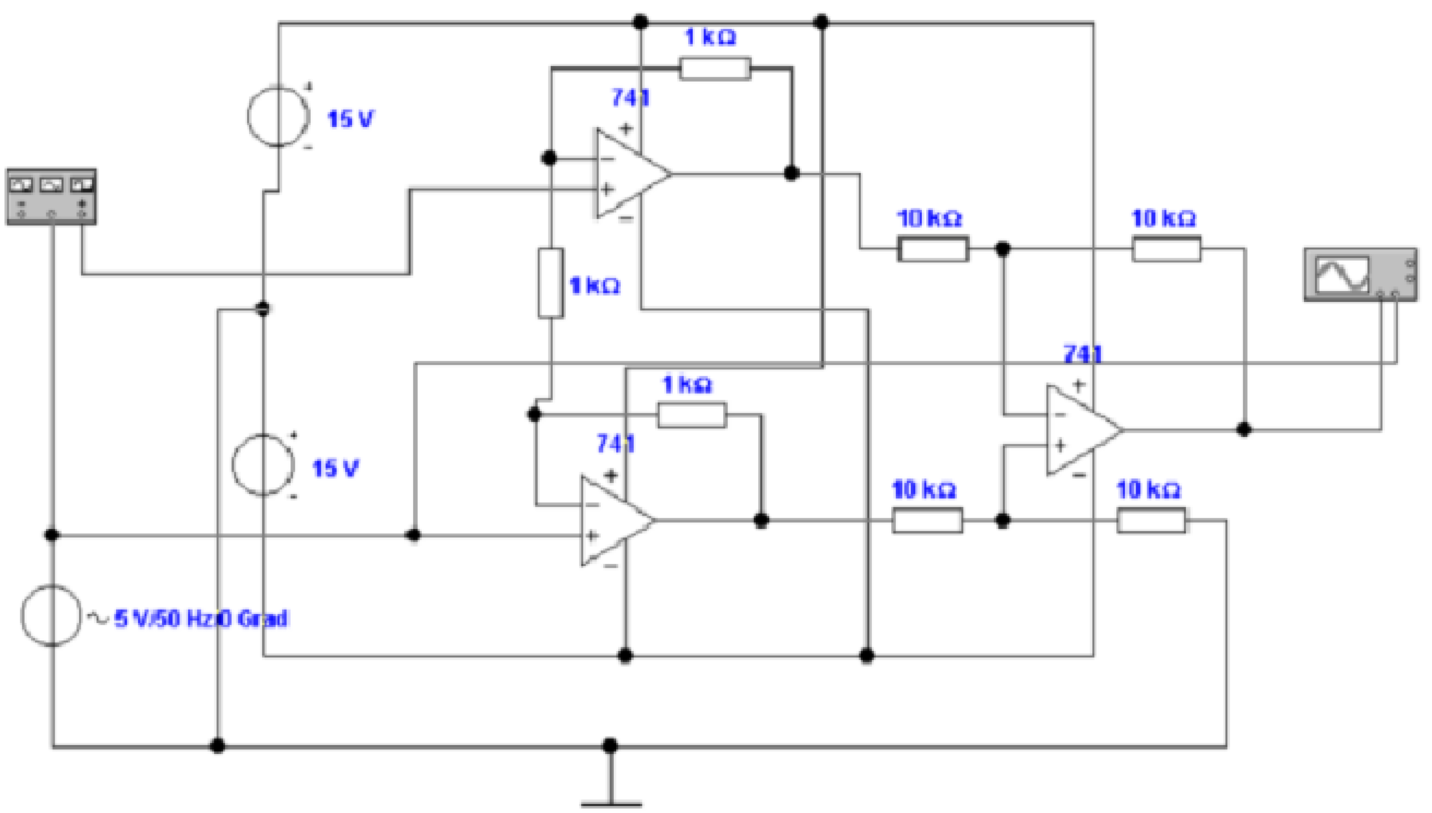
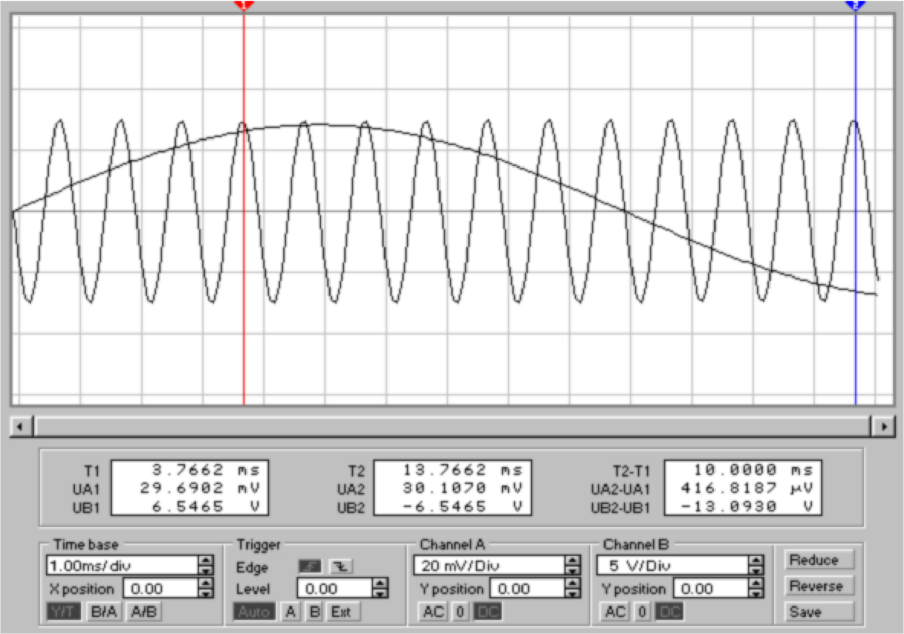
Abbildung 4.15 zeigt einen Instrumentenverstärker. Die
beiden Operationsverstärker am Eingang (links) sind als
nichtinvertierende Verstärker geschaltet. Da die Referenz nicht
das Erdpotential ist, sondern der jeweils andere Verstärker, ist
die Gleichtaktverstärkung 1. Der folgende Differenzverstärker
unterdrückt weiter das Gleichtaktsignal. Dieser dritte
Operationsverstärker muss eine gute Gleichtaktunterdrückung
besitzen.
4.1.3 Wechselstrom und Wechselspannung
Die Messung von Wechselspannungen aus Quellen mit
hohen Impedanzen ist eine schwierige Aufgabe. Solche
Quellen können unter anderem Photodioden oder die
Tunnelübergänge in einem STM (Scanning Tunneling
Microscope) sein. Insbesondere wenn die Quelle mit dem
Messverstärker über ein Koaxialkabel verbunden wird, kann
die Bandbreite der Messvorrichtung sehr eingeschränkt
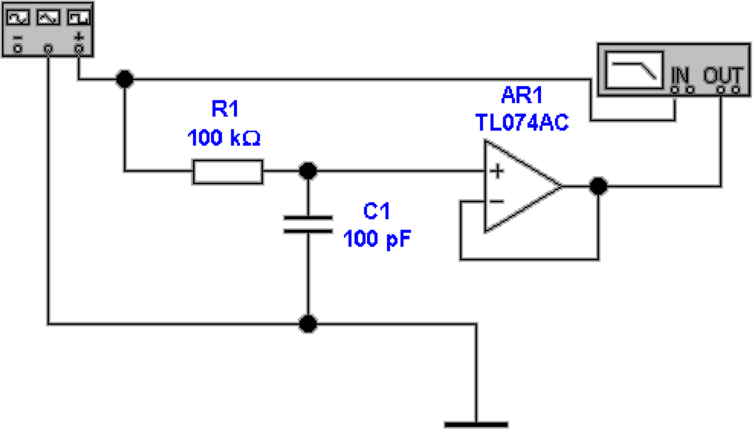
werden. Abbildung 4.19, links, zeigt ein Modell dieses
Messsystems. Die Spannungsquelle wird über ihren
Innenwiderstand von 100 kΩ an einen Spannungsverstärker
mit der Verstärkung 1 angeschlossen. Das Signal der Quelle
ist mit einem Koaxialkabel, Kapazität 100 pF, an den
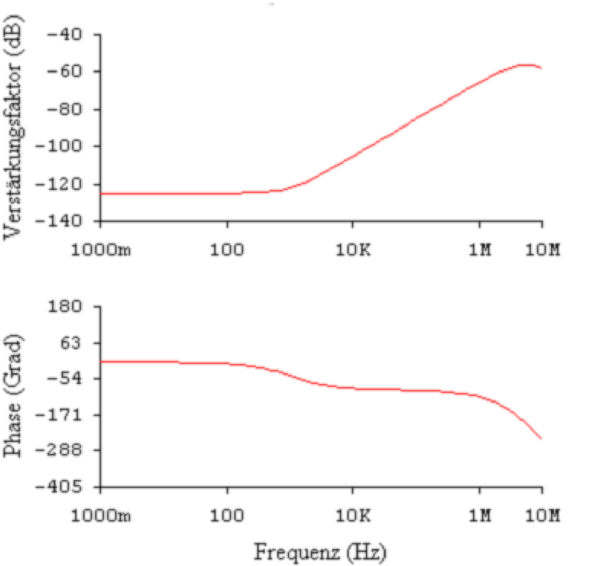
Verstärker angeschlossen. Die rechte Seite von Abb. 4.19 zeigt
das entsprechende Bode-Diagramm. Der Tiefpass aus
Innenwiderstand und Kabelkapazität bildet einen Tiefpass,
mit einer Zeitkonstante von 100pF × 100kΩ = 10μs.
Dies entspricht einer Grenzfrequenz von 16 kHz, wie sie
insbesondere aus dem Phasenbild ersichtlich ist.
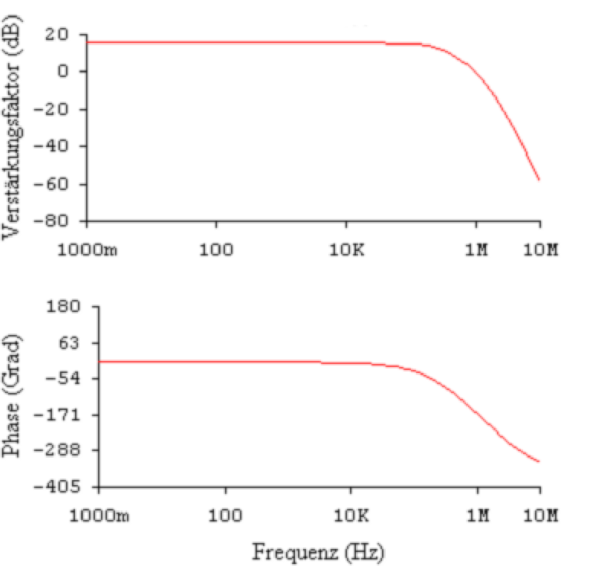
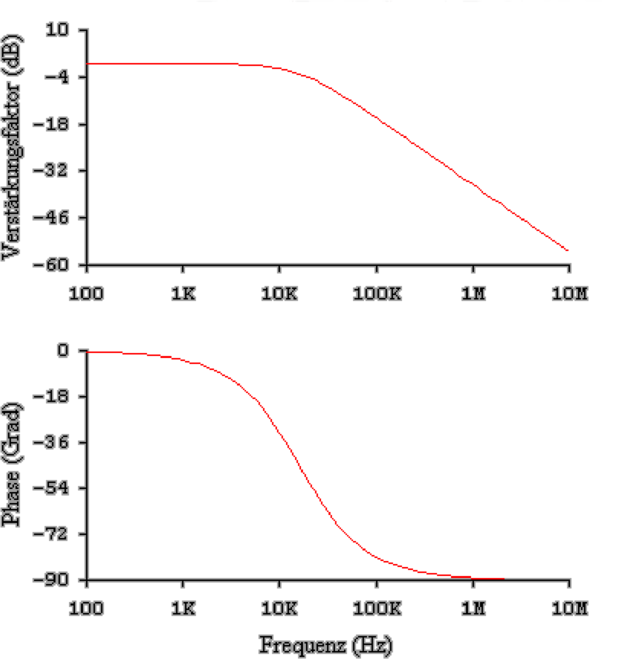
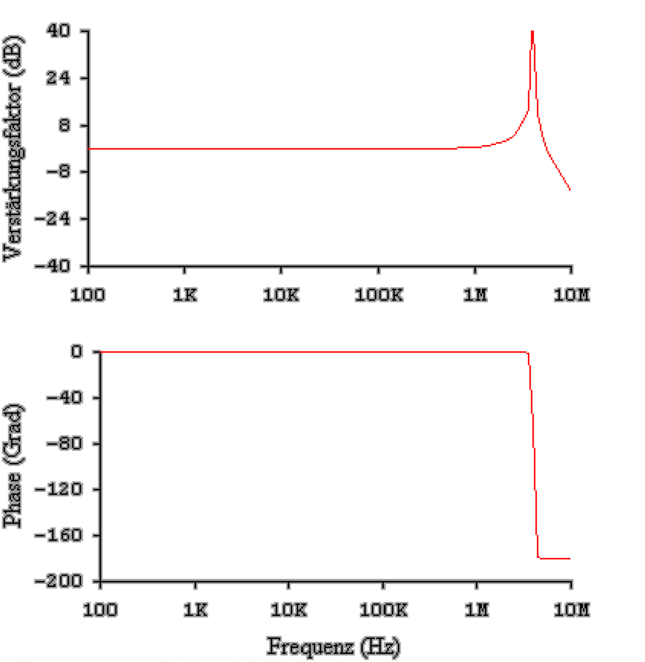
In Abb. 4.20 wurde der Schirm des Koaxialkabel, wie von
Tietze-Schenk[TS80] vorgeschlagen, an den Ausgang des
Operationsverstärkers gelegt. Die Bandbreite wird, wie im in
der Referenz angegebenen Buch beschrieben, breiter. Jedoch
entsteht bei hohen Frequenzen eine Resonanz. Diese
rührt von der Wechselwirkung der Phasenverschiebungen
des Operationsverstärkers mit denen des Koaxialkabels
her.
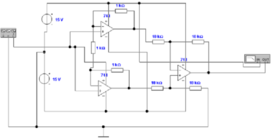
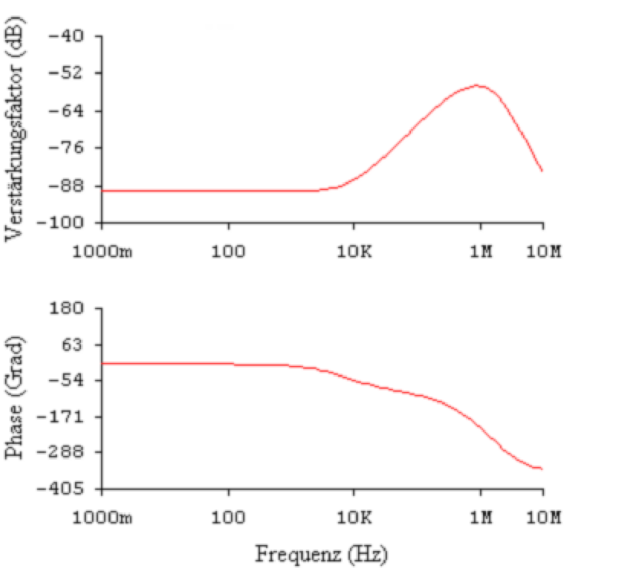
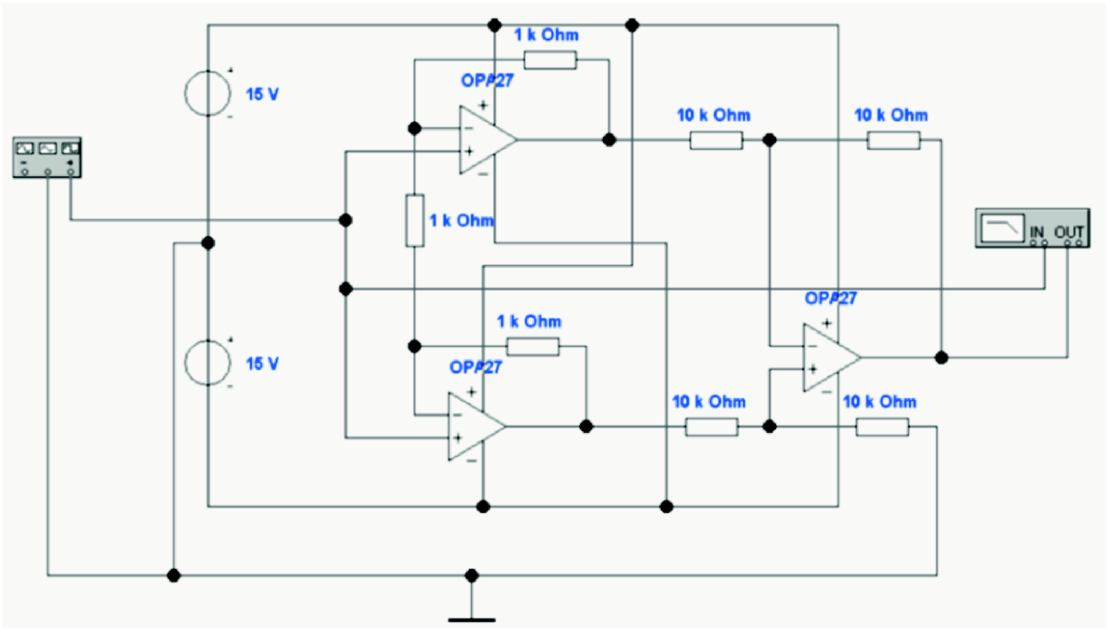
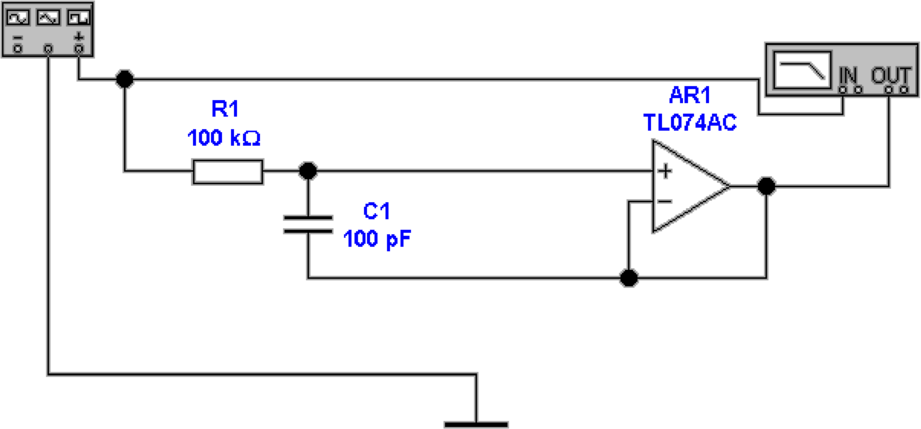
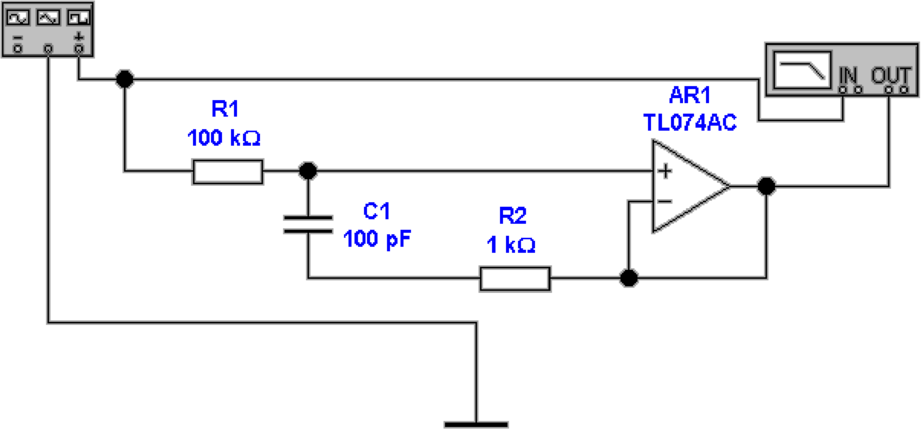
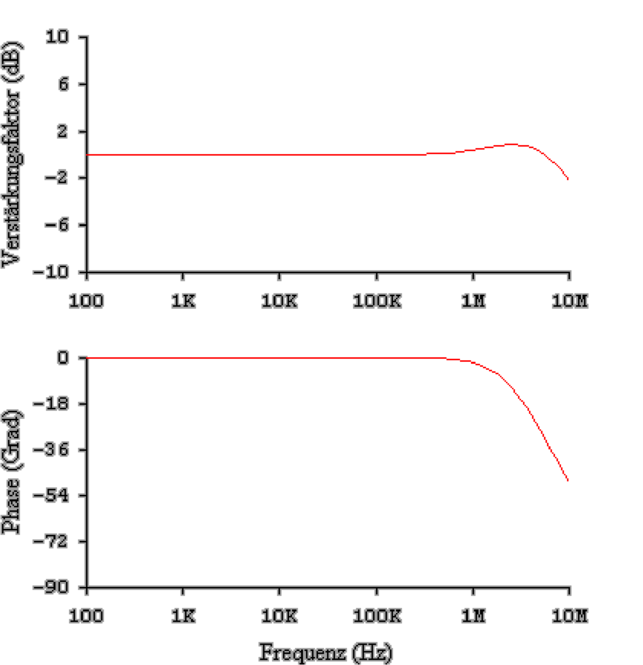
Diese Resonanz kann, wie in Abb. 4.21 gezeigt, gedämpft
werden, indem der Schirm des Koaxialkabels nicht
direkt, sondern über einen Widerstand von hier 1 kΩ
angeschlossen wird. Die Grösse des Widerstandes hängt
vom Operationsverstärker sowie von der Kabelkapazität
ab.
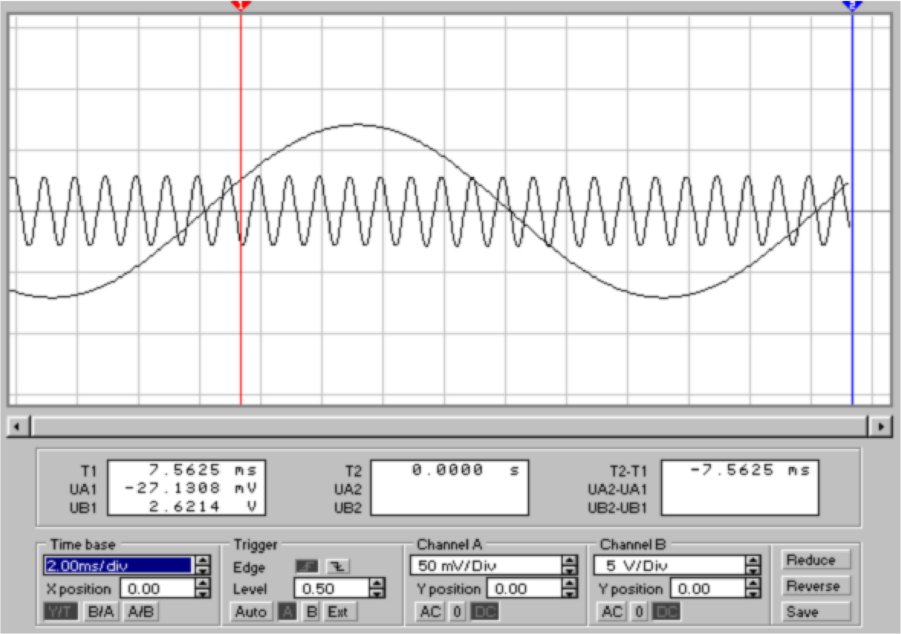
Zur Detektion von Wechselspannungen ist es nötig, die
Wechselspannung in eine Gleichspannung umzuwandeln.
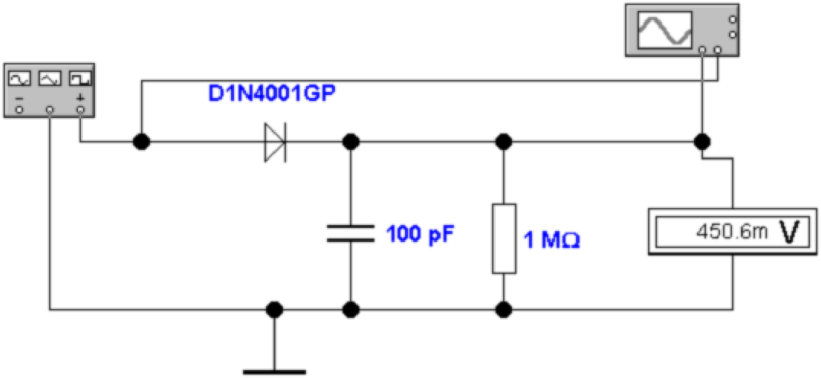
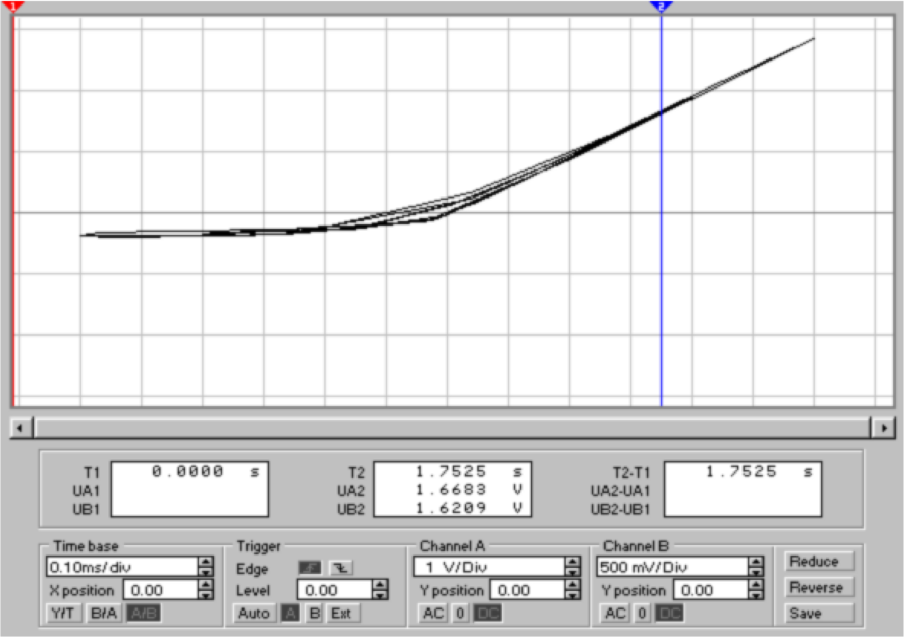
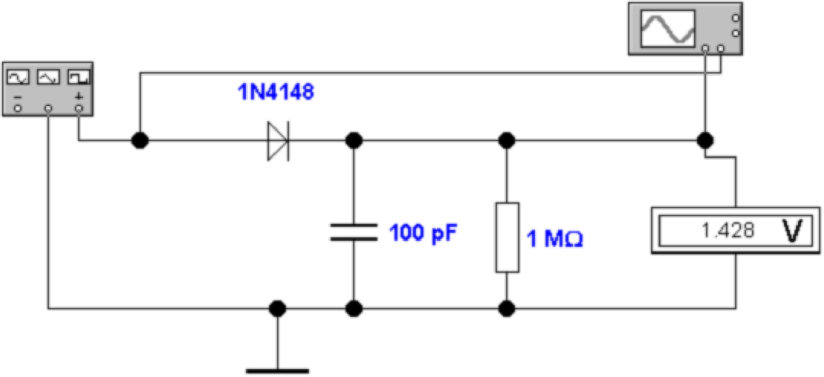
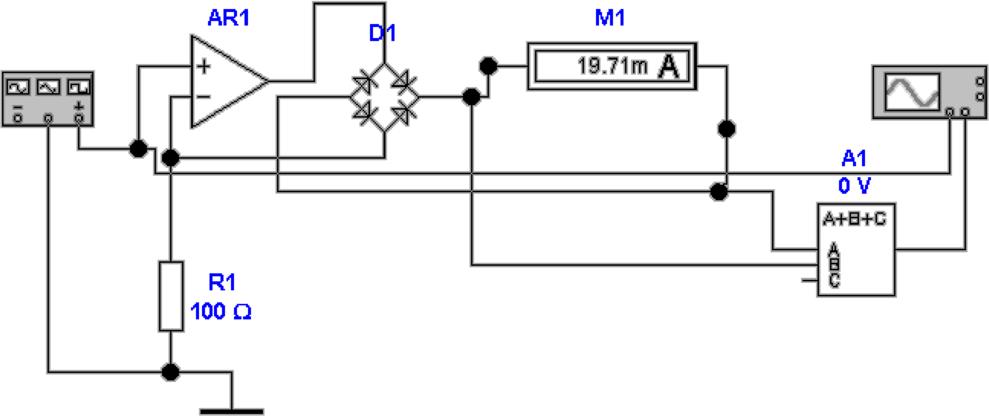
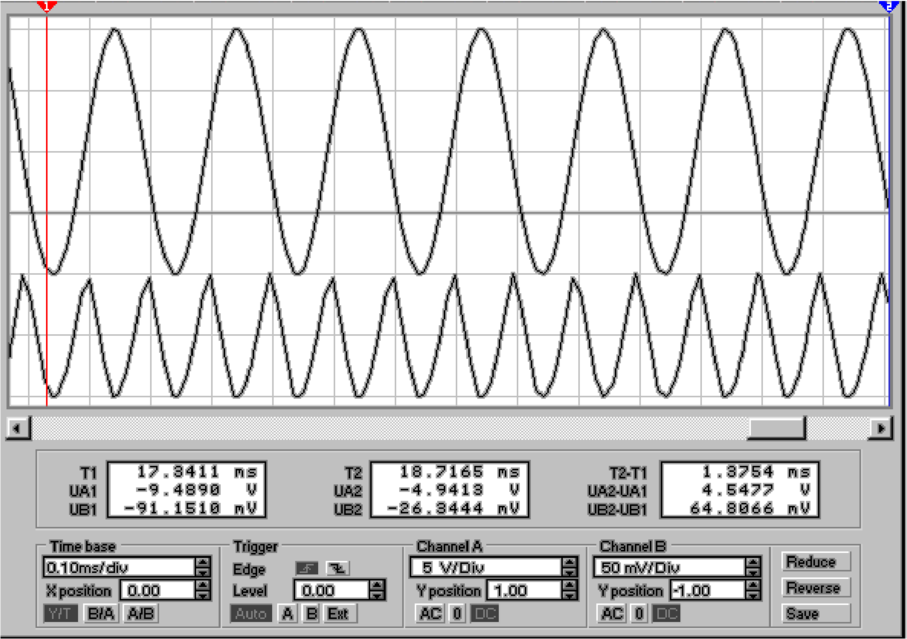
Abb. 4.22 zeigt eine entsprechende Schaltung. Das
Wechselspannungssignal wird über die Diode gleichgerichtet
und der Spitzenwert auf dem Kondensator akkumuliert.
Die Schaltung oben ist mit einer Diode 1N4001GP
aufgebaut. Bei hohem Frequenzen koppelt die beträchtliche
Sperrschichtkapazität der Diode das Hochfrequenzsignal über.
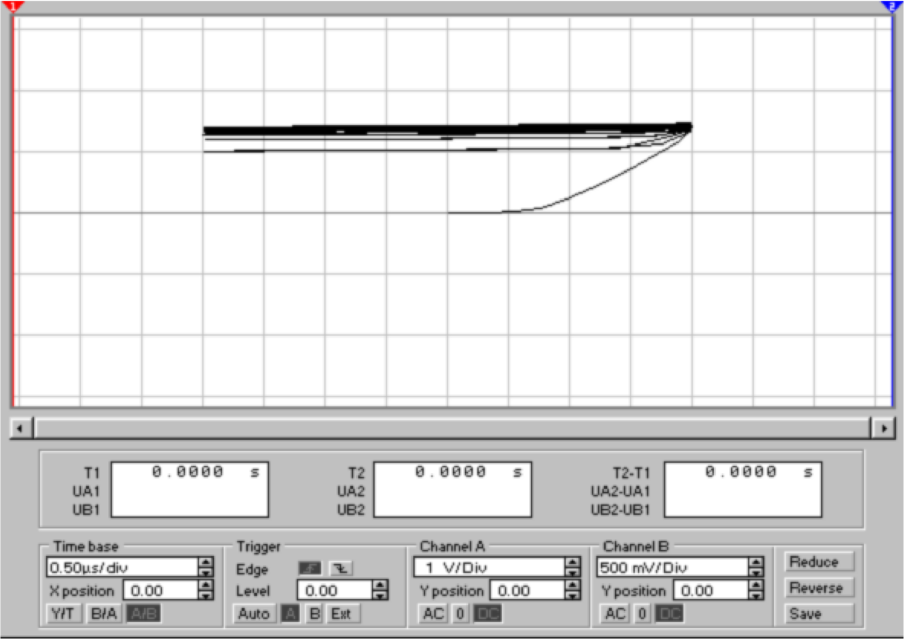
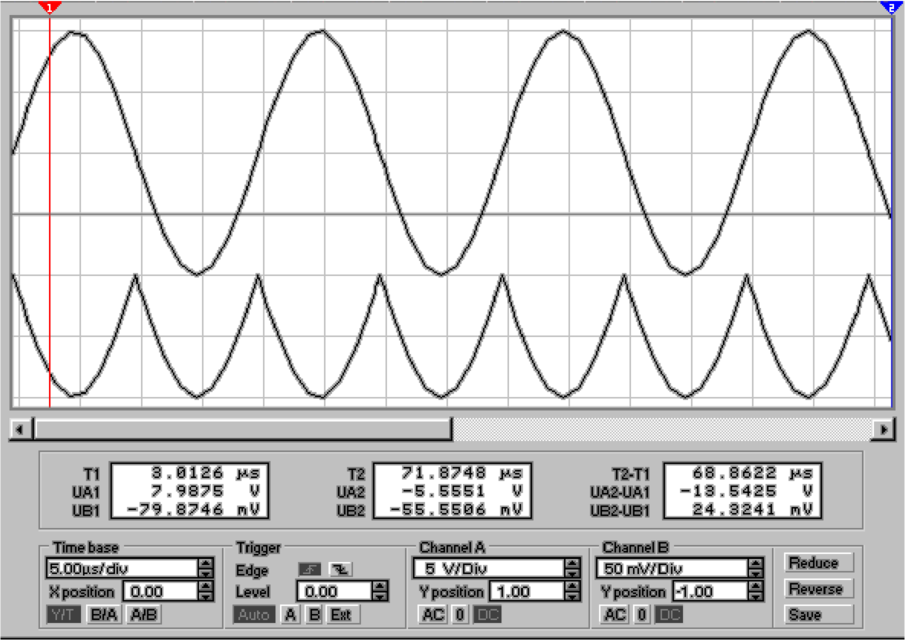
Besser ist es, eine Kleinsignaldiode wie die 1N4148 zu verwenden
(siehe Abb. 4.23). HF-Dioden, deren Sperrschichtkapazität
minimiert ist, sind eine ideale Wahl. In Frage kommt, u.A. der
Typ 1N914. Man beachte, dass die detektierte Spannung um
eine Diodendurchlassspannung geringer ist. Tabelle 4.1 gibt
für die beiden Dioden 1N4001 und 1N 4148 die gemessenen
Spannungen als Funktion der angelegten Spannung und der
Frequenz an. Aus dieser Tabelle wird schön ersichtlich, dass
bei der Diode 1N4001 die Sperrschichtkapazität die die
Brauchbarkeit limitierende Grösse ist. Generell ist das
Messresultat bei kleinen Spannungen nicht aussagekräftig.
|
|
|
|
|
|
| Frequenz | Anregung | 1N4148 | 1N4148 | 1N4001 | 1N4001 |
| | AC | DC | AC | DC | AC |
|
|
|
|
|
|
| 1 kHz | 4 V | 1.065 V | 1.33 V | 1.098 V | 1.551 V |
| 10 kHz | 4 V | 1.685 V | 1.033 V | 1.626 V | 1.215 V |
| 100 kHz | 4 V | 3.176 V | 243.3 mV | 2.095 V | 799.4 mV |
| 1 MHz | 4 V | 3.286 V | 42.56 mV | 1.273 V | 1.339 V |
| 10 MHz | 4 V | 3.321 V | 32.98 mV | -330.5 mV | 2.803 V |
| 100 MHz | 4 V | 1.294 V | 660.9 mV | -389.0 mV | 2.817 V |
|
|
|
|
|
|
| 1 kHz | 2 V | 413.2 mV | 554.0 mV | 481.0 mV | 799.5 mV |
| 10 kHz | 2 V | 731.0 mV | 449.0 mV | 741.9 mV | 623.7 mV |
| 100 kHz | 2 V | 1.377 V | 106.1 V | 943.4 mV | 422.8 mV |
| 1 MHz | 2 V | 1.410 V | 11.03 mV | 807.2 mV | 499.2 mV |
| 10 MHz | 2 V | 1.414 V | 1.111 mV | -285.7 mV | 1.389 V |
| 100 MHz | 2 V | 1.397 V | 109.5 μV | -378.8 mV | 1.408 V |
| 1 GHz | 2 V | 1.398 V | 63.80 μV | -418.2 mV | 1.410 V |
|
|
|
|
|
|
| 1 kHz | 1 V | 121.8 mV | 192.4 mV | 185.3 mV | 428.9 mV |
| 10 kHz | 1 V | 232.0 mV | 149.0 mV | 313.4 mV | 330.7 mV |
| 100 kHz | 1 V | 436.8 mV | 33.51 mV | 417.4 mV | 218.8 mV |
| 1 MHz | 1 V | 446.6 mV | 3.438 mV | 379.9 mV | 235.9 mV |
| 10 MHz | 1 V | 446.0 mV | 341.4 μV | 117.8 mV | 399.0 mV |
| 100 MHz | 1 V | 445.1 mV | 59.73 μV | -174.6 mV | 640.3 mV |
| 1 GHz | 1 V | 425.6 mV | 67.36 μV | -361.3 mV | 702.7 mV |
|
|
|
|
|
|
| 1 kHz | 0.5 V | 10.07 mV | 19.4 mV | 51.86 mV | 19.40 mV |
| 10 kHz | 0.5 V | 20.98 mV | 14.18 mV | 114.8 mV | 184.5 mV |
| 100 kHz | 0.5 V | 26.66 mV | 1.948 mV | 167.2 mV | 117.5 mV |
| 1 MHz | 0.5 V | 26.55 mV | 194.1 μV | 161.5 mV | 118.7 mV |
| 10 MHz | 0.5 V | 23.87 mV | 110.2 μV | 77.47 mV | 159.1 mV |
| 100 MHz | 0.5 V | 11.98 mV | 60.89 μV | -86.42 mV | 262.3 mV |
| 1 GHz | 0.5 V | 2.507 mV | 11.3 μV | -157.8 mV | 309.1 mV |
|
|
|
|
|
|
| 10 MHz | 0.1 V | 18 nV | 0 nV | 8.762 mV | 29.04 mV |
|
|
|
|
|
|
| |
| Tabelle 4.1.: | Gemessene Wechselspannungen mit den
Schaltungen 4.22 und 4.23. Für 100 MHz wäre die ideale
Gleichspannung nach dem Detektor 3.381V ≈ 4V − 0.7V
und die Wechselspannung wäre 355 μV. |
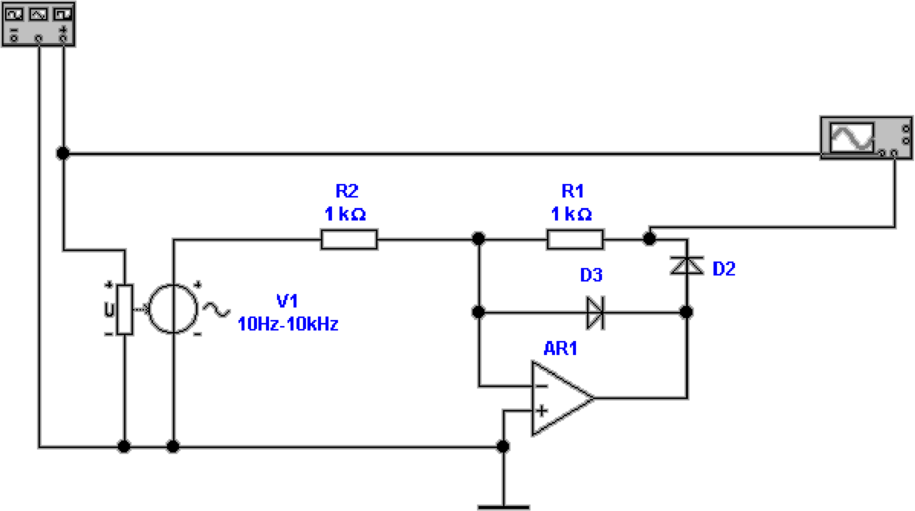
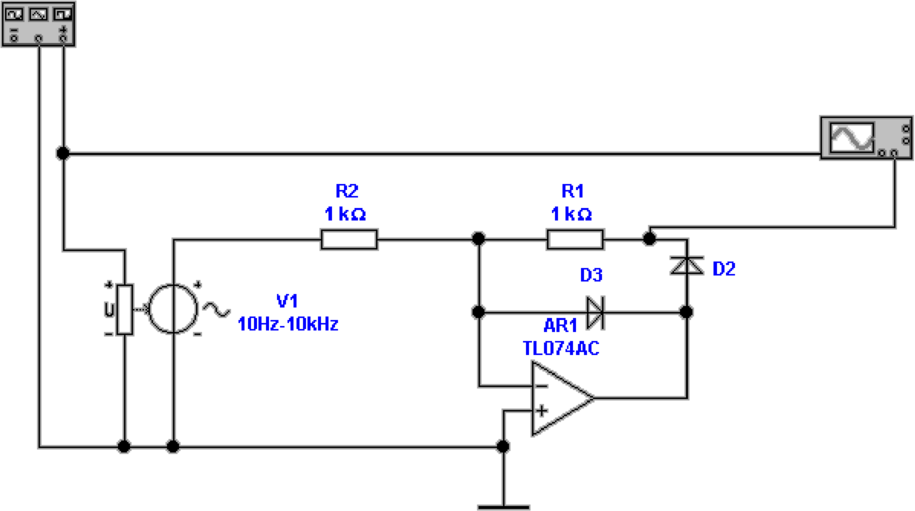
Abbildung 4.24 zeigt einen Halbwellengleichrichter
aufgebaut mit einem Operationsverstärker und zwei Dioden.
Die Schaltung funktioniert folgendermassen. Für die negative
Halbwelle (Ausgangsspannung von AR1 positiv) wird vom
Ausgang ein Strom geliefert, der durch D2, R1 und R2
fliesst. Da Die Verbindung zwischen R1 und R2 vom
Operationsverstärker virtuell auf Erde gehalten wird, gilt für
die Ausgangsspannung
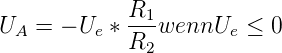 | (4.16) |
Die Diode D3 ist in Sperrichtung gepolt. Für die positive
Halbwelle ist D3 in Durchlassrichtung gepolt. Der Ausgang wird
über R1 und R2 vom Eingang mit Strom versorgt. Die Diode
D2 zieht nun den Ausgang auf eine Diodendurchlassspannung
über der Ausgangsspannung des Operationsverstärkers. Dieser
liegt aber, wegen der Durchlassspannung von D3 auf - einer
Diodendurchlassspannung. Also ist der Ausgang auf 0 V. Die
Schaltung 4.24 ist also ein Halbwellengleichrichter.
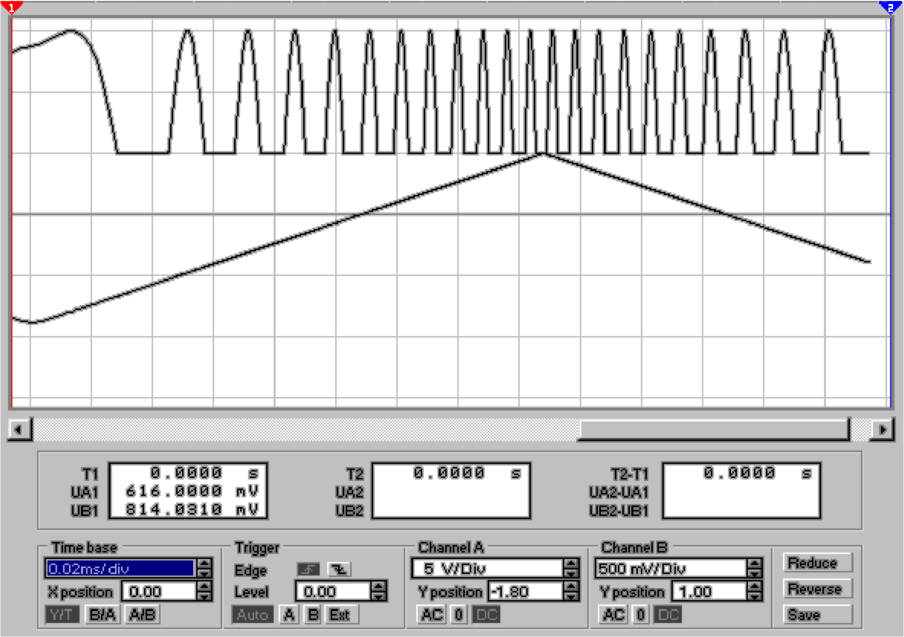
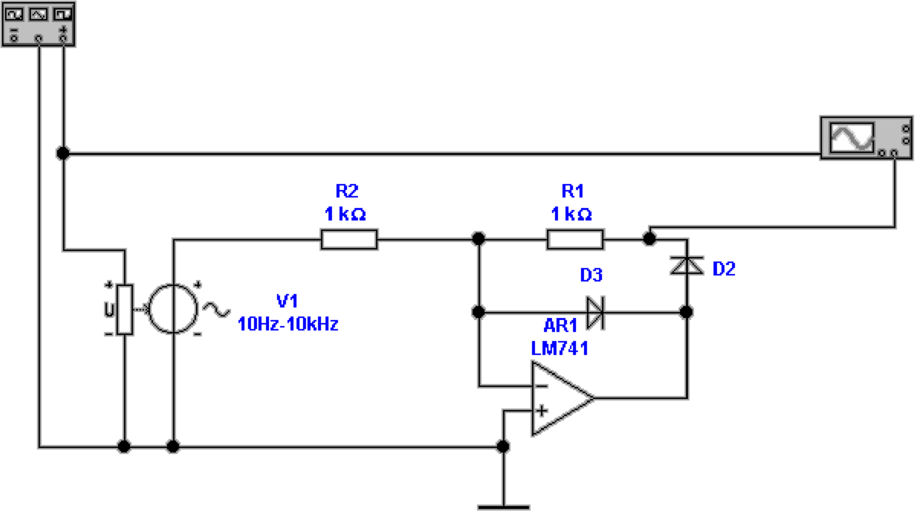
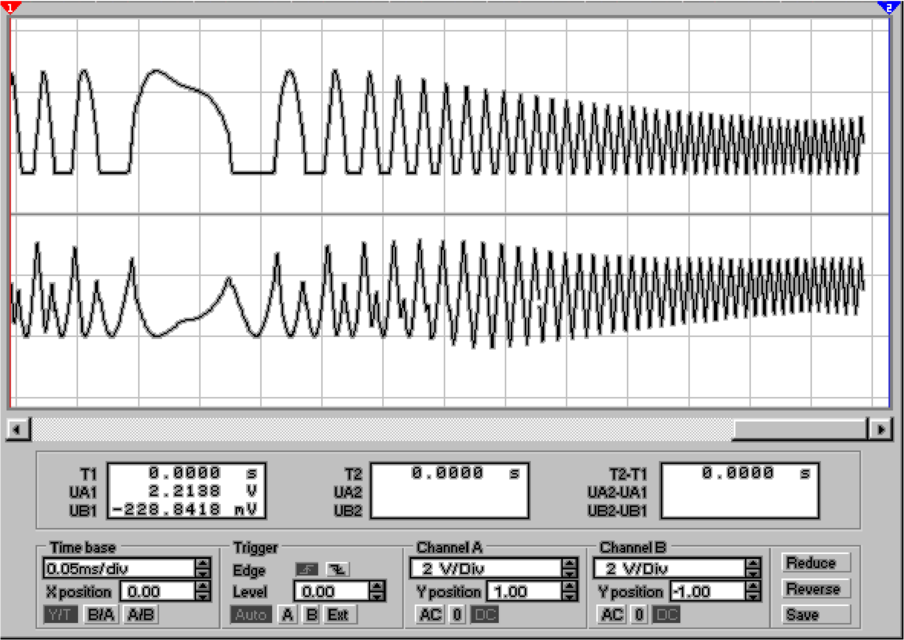
Während die Schaltung in Abbildung 4.24 mit einem idealen
Operationsverstärker aufgebaut ist, ist die in Abb. 4.25 mit
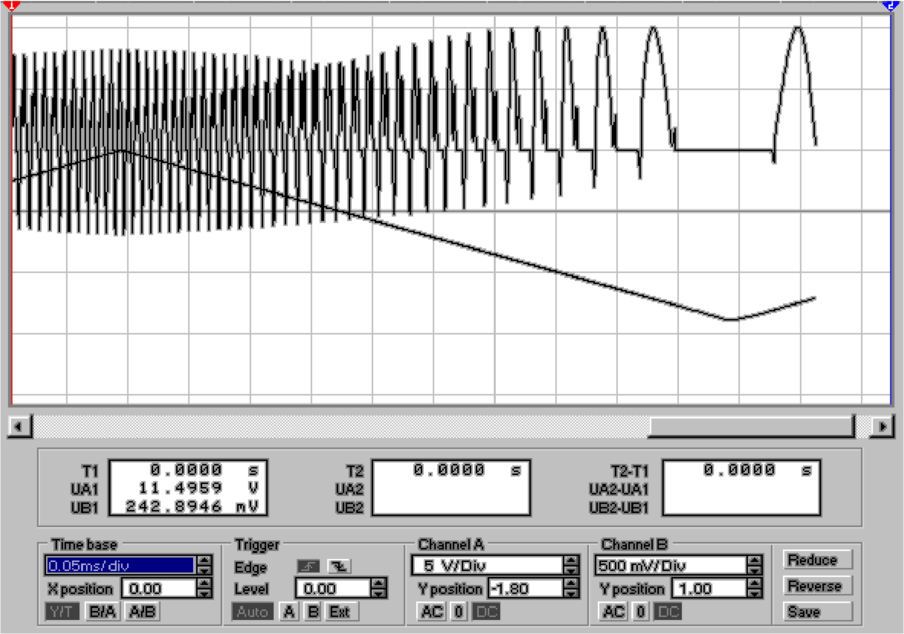
einem LM741 aufgebaut. Die Schaltung hat bei Frequenzen
über einigen 100 Hz kein Gleichrichterverhalten mehr.
Grund dafür ist die bescheidene Slew-Rate (Anstiegszeit)
dieses Verstärkers. Immer wenn das Vorzeichen des
Eingangssignales wechselt, muss eine Spannung von zwei
Diodendurchlassspannungen übersprungen werden. Dies
bedeutet beim LM741 eine Zeitverzögerung von etwa 2 μs.
Diese, auf den ersten Blick unbedeutende Verzögerung
ist jedoch für das schlechte Verhalten verantwortlich.
Durch die Zeitverzögerung entsteht im Regelkreis des
Operationsverstärkers eine Überkompensation.
Für die Schaltung des Halbwellengleichrichters aus
Abb. 4.25 werden Verstärker mit einer schnellen
Anstiegsgeschwindigkeit des Ausgangssignals benötigt.
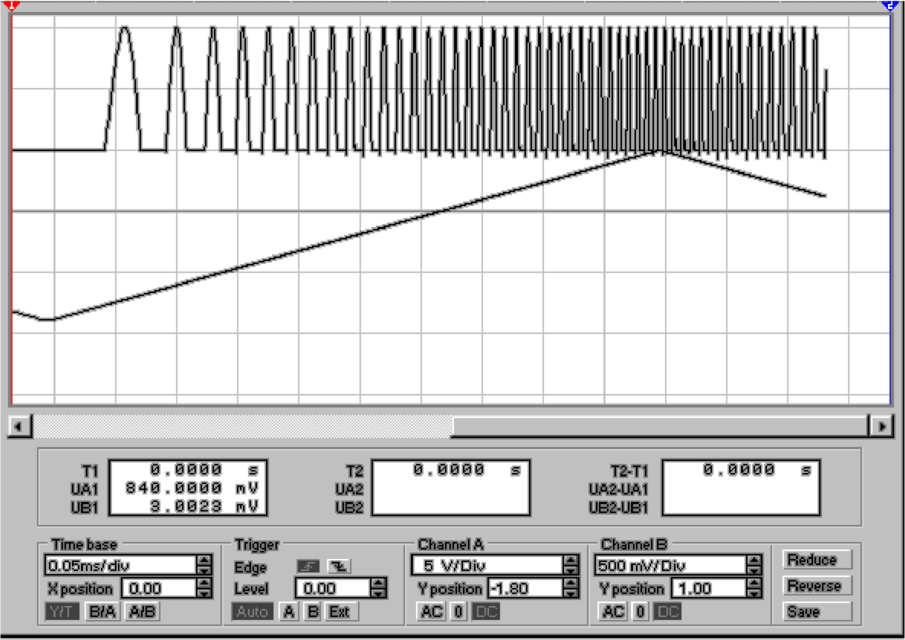
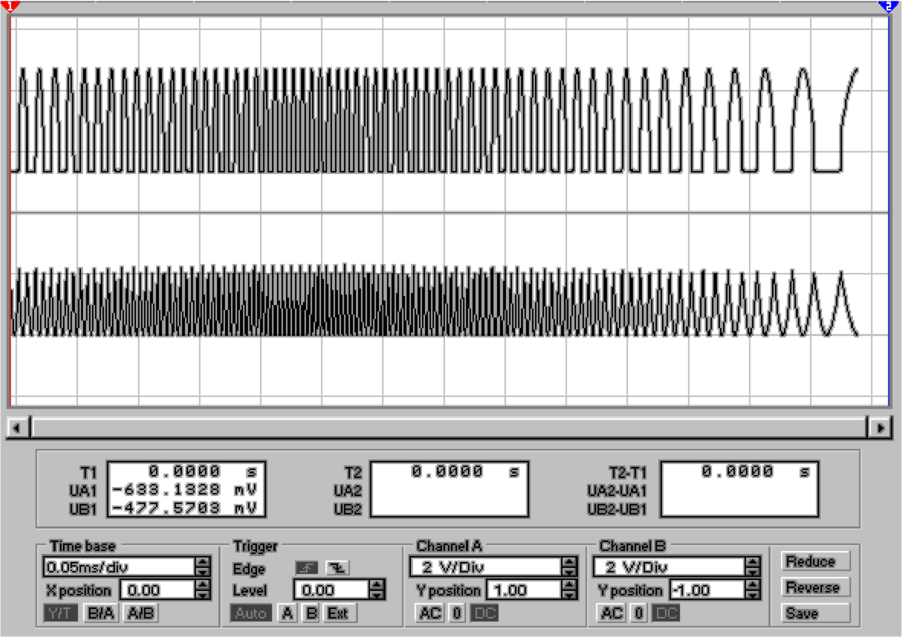
Abb. 4.26 zeigt die gleiche Schaltung aufgebaut mit einem
TL074. Nun ist das Ausgangssignal bis zu 10 kHz von
befriedigender Güte. Höhere Frequenzen können mit dieser
Schaltung jedoch nur schwer vernünftig gleichgerichtet
werden.
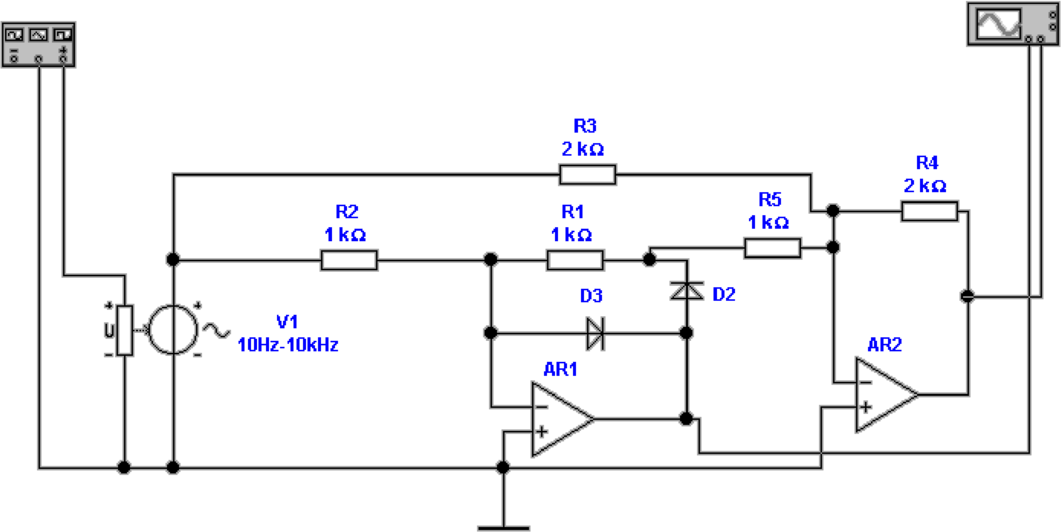
Abb. 4.27 zeigt, wie die Schaltung aus Abb. 4.26 zu einem
Vollwellengleichrichter ausgebaut werden kann. Die Idee
ist die folgende Dem Halbwellengleichrichter wird ein
invertierender Verstärker parallelgeschaltet, der neben dem
Eingangssignal auch den Ausgang des Halbwellengleichrichters
mit doppeltem Gewicht verstärkt. Wir erhalten dann für die
positive Halbwelle Ue ≥ 0
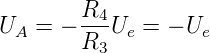 | (4.17) |
und für die negative Halbwelle Ue ≤ 0
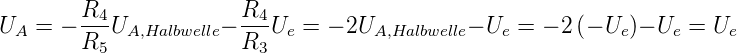 | (4.18) |
In der Summe ergibt sich also (für Ue < 0 ist Ue = −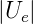 !)
!)
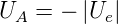 | (4.19) |
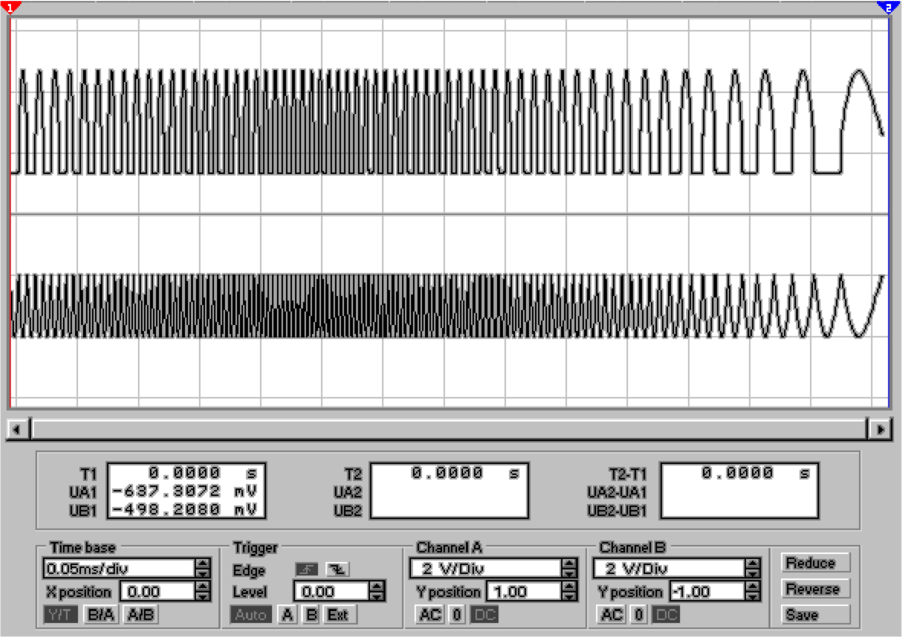
Wieder ist die Schaltung aus Abb. 4.27 als ideale Schaltung
nicht repräsentativ für die Güte realer Schaltungen. Abb.
4.28 zeigt wieder, dass Verstärker vom Typ LM741 nicht
brauchbar für diese Anwendung sind, sie könnten höchstens
bis einige 10 Hz verwendet werden.
Schliesslich ist aus Abb. 4.29 ersichtlich dass ein
Vollwellen-Präzisionsgleichrichter mit dem TL074 bis 10 kHz
arbeiten kann.
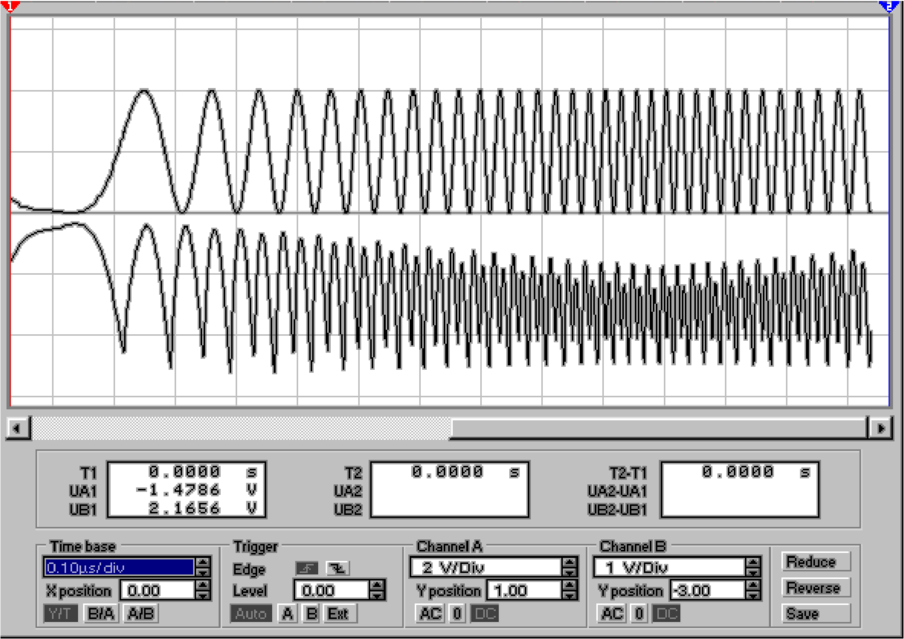
Wesentlich besser als die Operationsverstärkerschaltungen
sind Transistorschaltungen als Gleichrichter für höchste
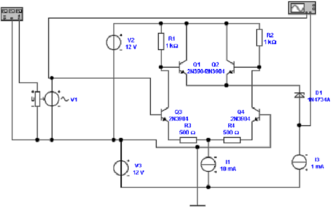
Frequenzen geeignet. Abb. 4.30 zeigt eine mögliche
Implementation eines Transistoren-Vollwellengleichrichters.
Die Transistoren Q3 und Q4 bilden einen Differenzverstärker.
Die Transistoren Q1 und Q2, deren Emitter und Kollektoren
zusammengeschaltet sind, verstärken jeweils das positivere
Potential. So kommt eine Vollwellengleichrichtung zustande.
Die Schaltung nach Abb. 4.30 kann bei geeigneter Wahl der
Transistoren mit bis zu 100 MHz betrieben werden.
Abbildung 4.31 zeigt einen
True-RMS-Gleichrichter .
Die vorherigen Schaltungen haben den Betrag der
Wechselspannung bestimmt. Nun ist der Betrag jedoch
längstens nicht so interessant wie die dissipierte Leistung an
einem Widerstand. Es ist bekannt, dass
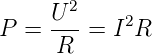 | (4.20) |
Deshalb ist, wenn man Signalformen sucht, die die gleiche
dissipierte Leistung an einem Widerstand R erzeugen. Die
Grösse
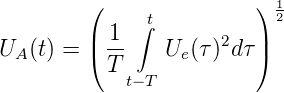 | (4.21) |
sehr viel interessanter. Dies ist die Definition des
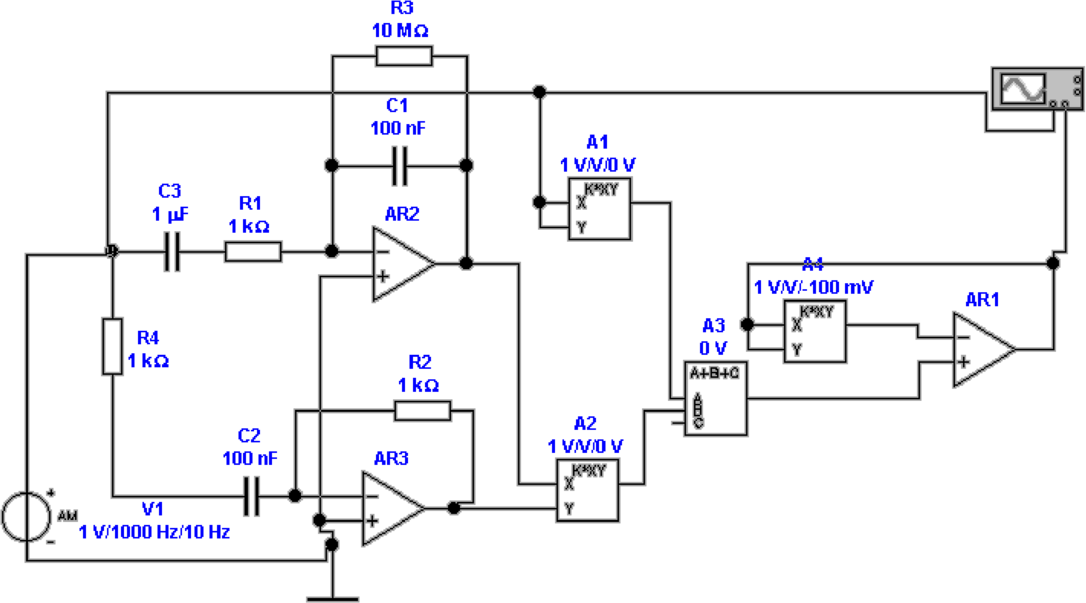
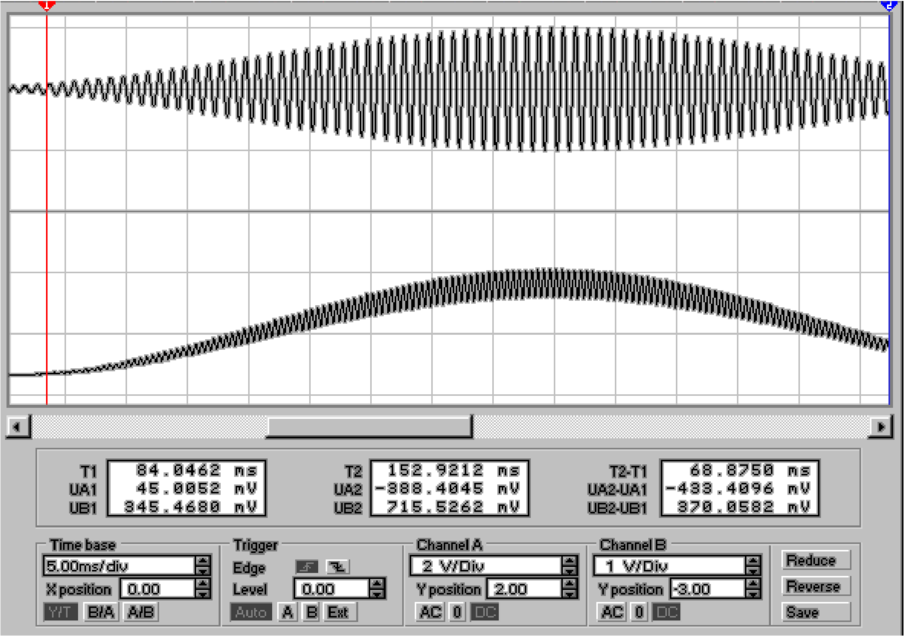
RMS-Wertes. Die Schaltung in Abbildung 4.31 ist eine
Implementation dieser Gleichung. Von links gesehen folgt
zuerst ein Quadrierer, dann ein Integrator in Form
eines Tiefpassfilters und zu letzt ein Radizierer. Dieser
Schaltungsteil benützt die Tatsache, dass eine Impedanz im
Rückkopplungszweig eines Operationsverstärkers sich zur
dualen Funktion transformiert, das heisst vom Quadrat zur
Wurzel, von der Exponentialfunktion zum Logarithmus.
Abb. 4.32 zeigt einen Vektormesser. Die Idee dahinter
ist, wenn ich A cos ωt und A sin ωt habe, dann kann ich
mit
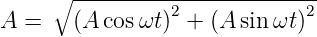 | (4.22) |
rechnen. Angewandt auf die Schaltung von Abb. 4.32 führt
dies zu
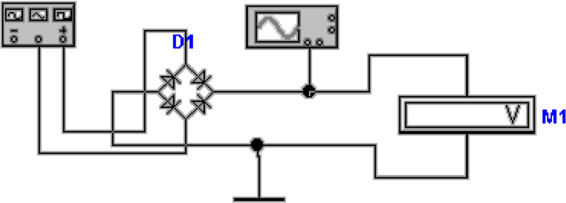
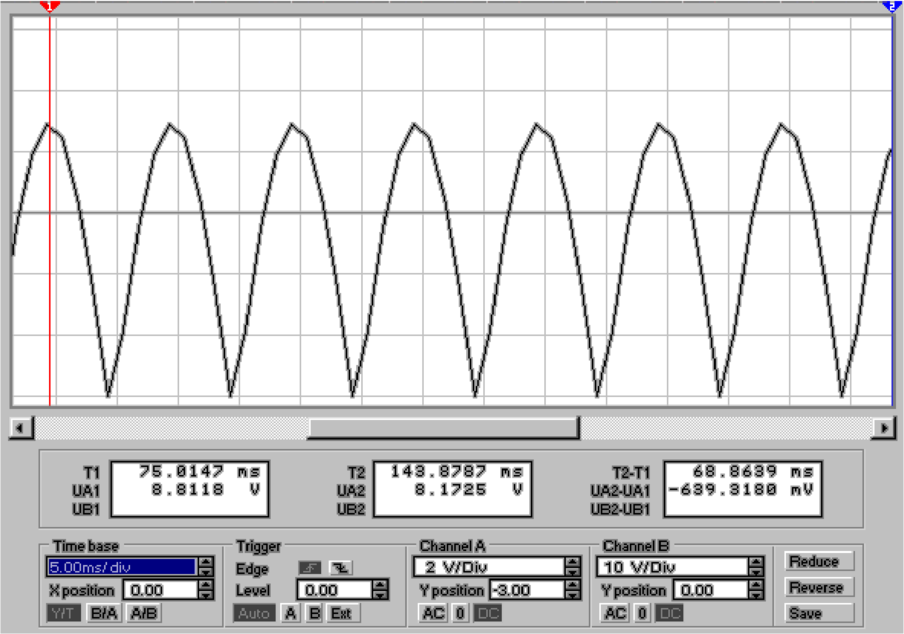
Abb. 4.33 zeigt eine Brückenschaltung nach Graetz. Die
Dioden oben rechts und unten links oder die Dioden oben links
und unten rechts sind jeweils in Durchlassrichtung geschaltet.
Im Diagonalzweig der Brücke steht die gleichgerichtete
Spannung zur Verfügung. Die Schaltung hat zwischen dem
Eingangsteil und dem Ausgangsteil kein gemeinsames
Bezugspotential .
Die Graetz-Schaltung wird vorwiegend zur Gleichrichtung
nach einem Trenntransformator verwendet.
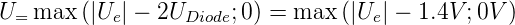 | (4.27) |
Abb. 4.34 zeigt eine zu 4.33 analoge Schaltung. Dadurch,
dass der Brückengleichrichter im Rückkoppelzweig ist,
arbeitet die Schaltung mit eingeprägtem Strom. Die
Spannungsabfälle über den Dioden werden so kompensiert.
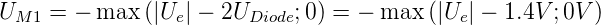 | (4.28) |
Schliesslich zeigt Abb. 4.35 eine Brückenschaltung mit
getrenntem Transformator. Die Schaltung ist besonders
geeignet, wenn Transformatoren billig im Vergleich zu Dioden
sind. Weiter ist der Spannungsabfall
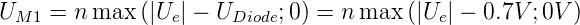 | (4.29) |
nur eine Diodenspannung. In Gleichung (4.29) ist n das
Übertragungsverhältnis von T1.
4.1.4 Ladung
Die Messung von Ladung stellt eines der schwierigeren
Messprobleme dar. Um Ladung messen zu können, muss
Energie auf das Messwerk übertragen werden. Typische
Energien sind jedoch
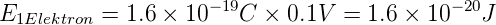 | (4.30) |
also sehr klein.
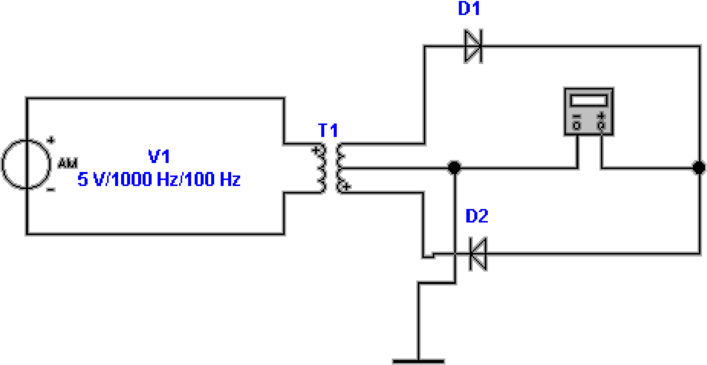
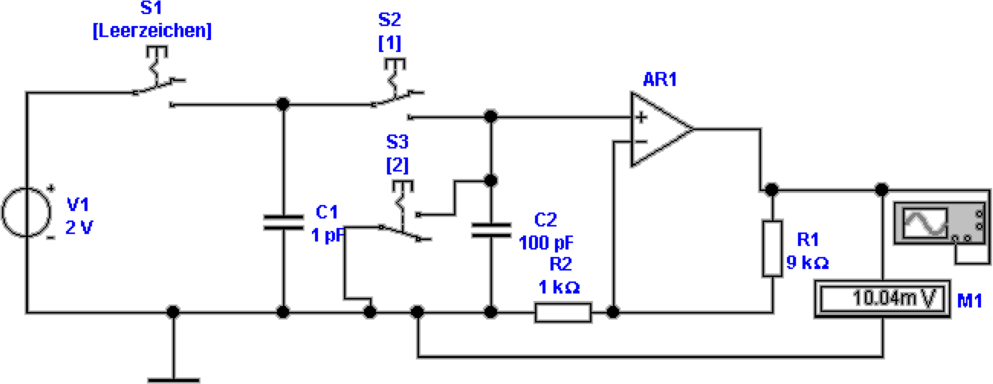
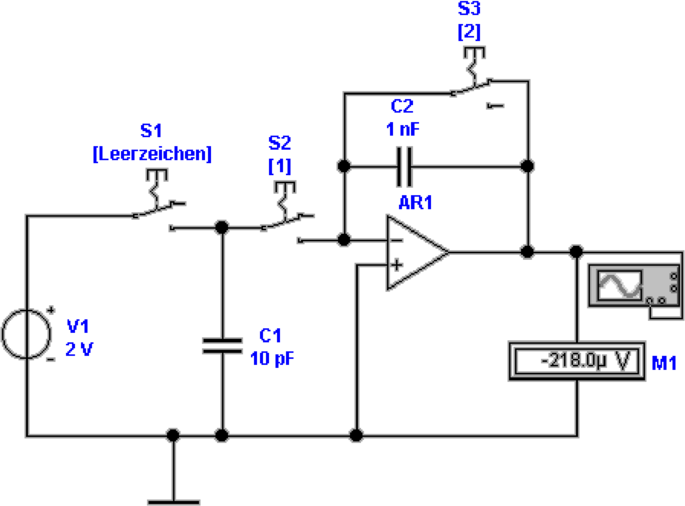
Abbildung 4.36 zeigt eine Schaltung, mit der Ladungen
gemessen werden können. Ziel ist, die Ladung auf dem
Kondensator C1 zu messen. Damit Die Ladung möglichst
vollständig transferiert werden kann, muss die Kapazität C2
sehr viel grösser als die von C1 sein.
Vor dem Schliessen von S2 gilt
Wird S2 geschlossen gilt für die Ladungen 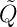 1 und
1 und 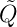 2 sowie
das Spannungsgleichgewicht dass
2 sowie
das Spannungsgleichgewicht dass
Daraus folgt:
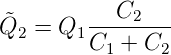 | (4.31) |
gilt. Wenn C2 »C1 gilt, dann wird praktisch alle Ladung
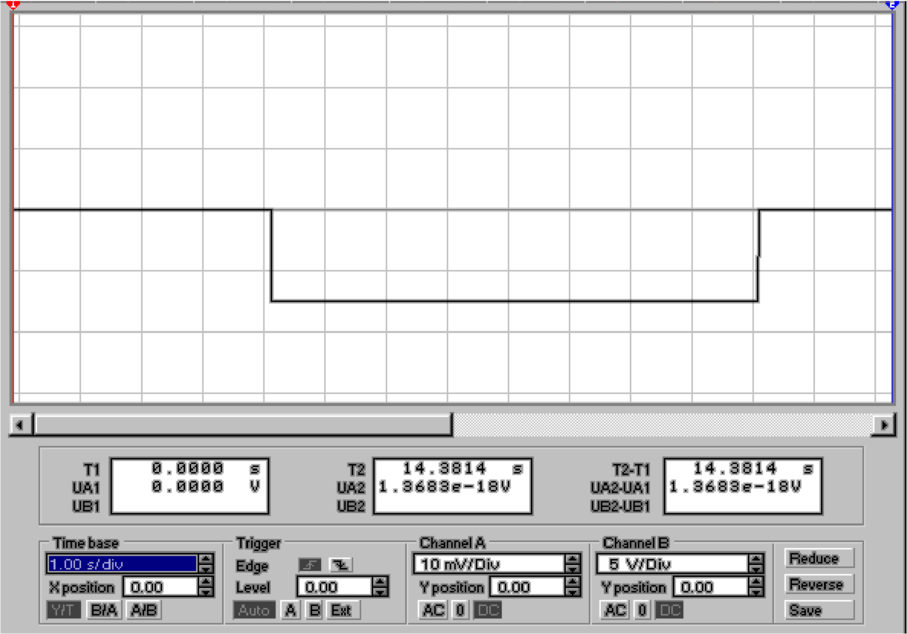
von C1 auf C2 übertragen und 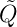 2 = Q1. S3 dient zum
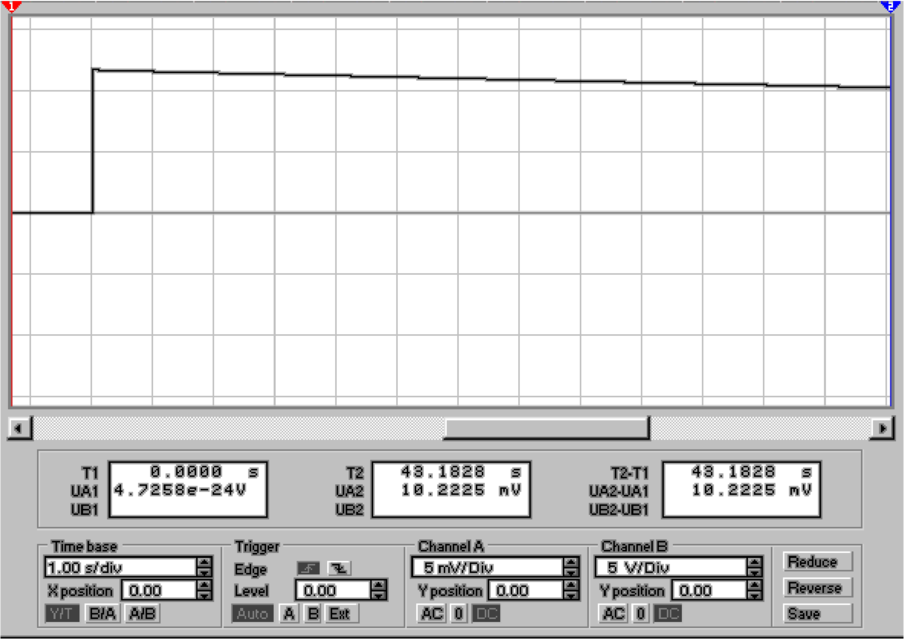
Entladen des Messkondensators C2. Aus der unteren Hälfte
von 4.36 ersieht man, dass die Ausgangsspannung einen
Sprung von der Grösse UC2 =
2 = Q1. S3 dient zum
Entladen des Messkondensators C2. Aus der unteren Hälfte
von 4.36 ersieht man, dass die Ausgangsspannung einen
Sprung von der Grösse UC2 = 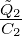 =
= 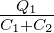 macht. Ebenso ist
ersichtlich, dass Die Spannung sehr schnell wieder abnimmt,
da Leckströme sogar im Modell eines idealen Verstärkers nicht
zu vermeiden sind.
macht. Ebenso ist
ersichtlich, dass Die Spannung sehr schnell wieder abnimmt,
da Leckströme sogar im Modell eines idealen Verstärkers nicht
zu vermeiden sind.
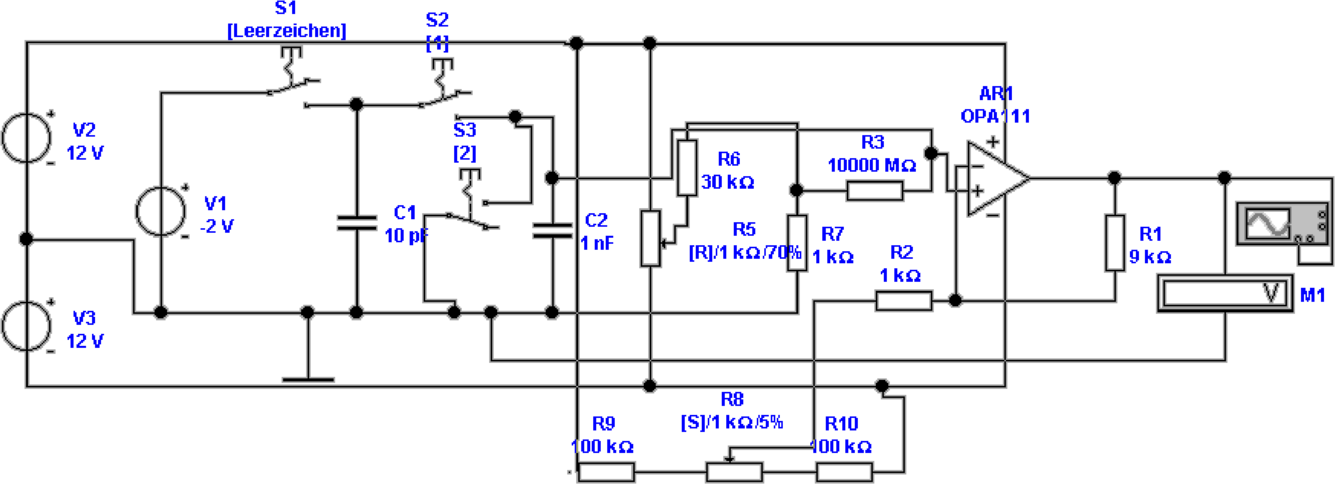
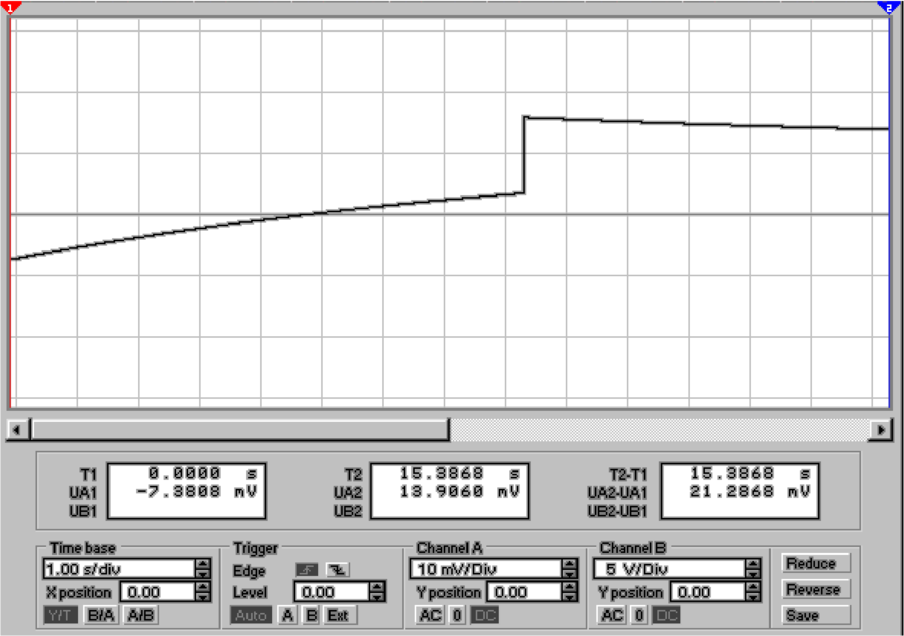
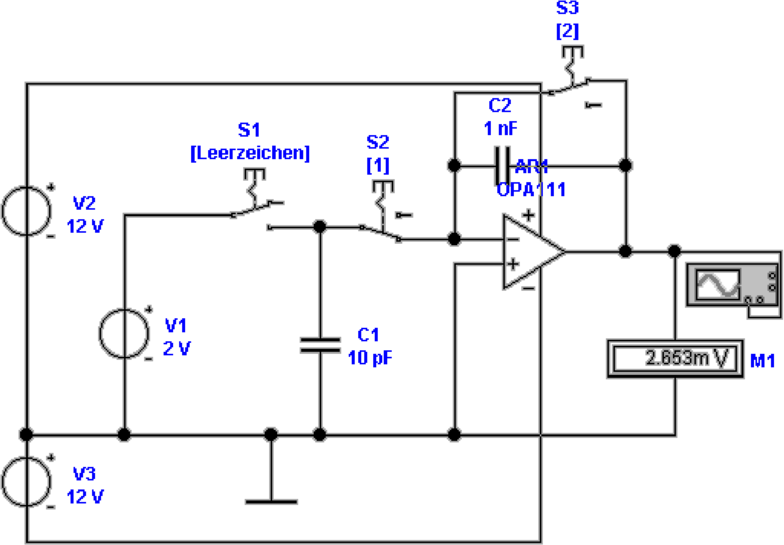
Zum Vergleich mit einem idealen Operationsverstärker in
4.36 zeigt Abb. 4.37 die gleiche Schaltung mit einem realen
Verstärker. Die Widerstände R3, R5, R6 und R7 dienen zur
Kompensation des Bias-Stromes im invertierenden Eingang
von AR1. Die Widerstände R2, R8, R9 und R10 dienen zur
Kompensation der Offsetspannung. Nur mit diesen beiden
Massnahmen ist es möglich, ein Signal wie in Abb. 4.37 zu
bekommen. Wieder ist der Spannungssprung das Mass für die
Ladung, der restliche Kurvenverlauf hängt von Störeinflüssen
ab.
Abbildung 4.38 zeigt die Ladungsmessung mit einem
Integrator. Die Verstärkung des Operationsverstärkers AR1
bewirkt, dass der Kondensator C1 vollständig entladen wird.
Der resultierende Strom lädt wieder, ohne Verluste, C − 2 auf.
man erhält also
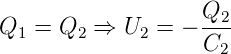 | (4.32) |
Wie die rechte Seite von Abb. 4.38 zeigt, entsteht
nach dem Anlegen von C1 am Ausgang von AR1 ein
Spannungssprung. Anders als in der Schaltung von Abb. 4.36
ist das Ausgangssignal konstant. Hier zeigt sich der Vorteil,
wenn man die Eingänge der Operationsverstärker in der Nähe
des Spannungsnullpunktes hält.
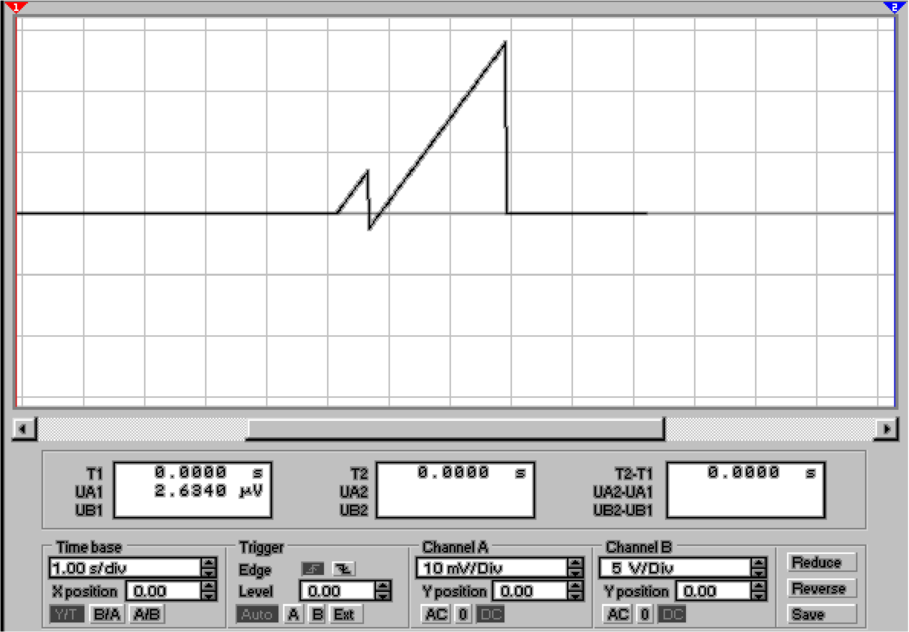
Der reale Operationsverstärker in Abb. 4.39 erzeugt genauso
eine Rampe. Hier wurde keine Kompensationsschaltung
verwendet: deshalb die doch steilen Spannungsverläufe.
Wieder ist der Spannungssprung das Mass für die Ladung,
und nicht der sonstige Spannungsverlauf.
4.1.5 Widerstand
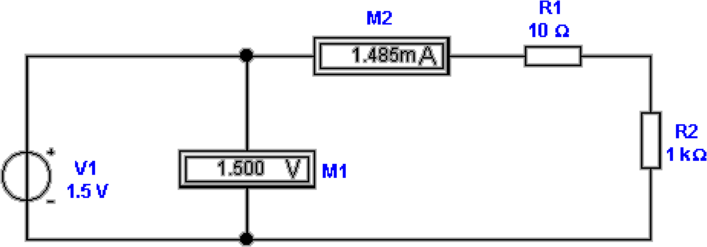
In Abb. 4.40 wird die stromrichtige Messung eines
Widerstandswertes gezeigt. Die Spannung U wird über das
Strommessgerät M2 mit seinem Innenwiderstand R1 an den
zu messenden Widerstand R2 gelegt. Die Messung heisst
stromrichtig, da der Strom durch R2 richtig gemessen
wird, jedoch der Spannungsabfall an R1 meistens nicht
berücksichtigt wird. Ist R1 bekannt, kann man mit
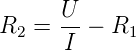 | (4.33) |
den genauen Wert von R2 bestimmen. Eingesetzt ergibt
sich:
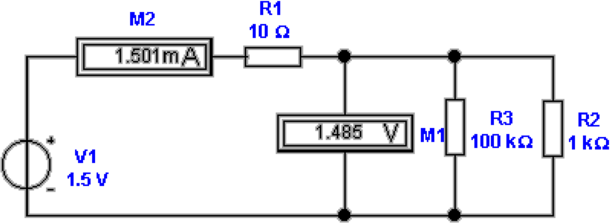
Abbildung 4.41 zeigt eine spannungsrichtige
Widerstandsmessung. Hier ist das Spannungsmessgerät M1
parallel zum zu messenden Widerstand angeschlossen. Die
Spannung am Widerstand wird also richtig gemessen.
Der Strom, den das Ampèremeter M2 misst, setzt sich
aus dem Strom durch den zu prüfenden Widerstand R2
sowie aus dem Strom durch den Innenwiderstand R3 des
Spannungsmessers zusammen. Is R3 bekannt, so ergibt
sich
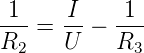 | (4.34) |
Andernfalls muss sichergestellt werden, dass R2 «R3 ist.
Setzt man die Werte aus Abbildung 4.41 in Gleichung (4.34)
ein, erhält man
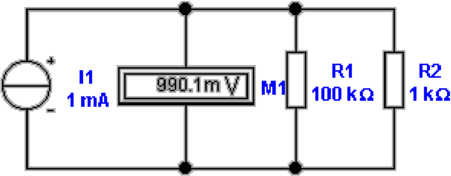
Die Widerstandsmessung kann vereinfacht werden,
wenn man anstelle einer Spannungsquelle eine bekannte
Stromquelle einsetzt (siehe Abb. 4.42). Wieder wird damit,
spannungsrichtig, der Parallelwiderstand aus R2 sowie dem
Innenwiderstand des Spannungsmessers, R1, gemessen.
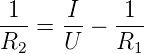 | (4.35) |
Die Werte aus Abbildung 4.42 ergeben
Ist der Innenwiderstand R1 des Spannungsmessers
nicht genau bekannt, muss man die Annahme R1 » R2
machen.
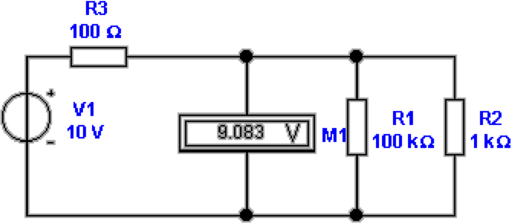
Abb. 4.43 zeigt eine Widerstandsmessung mit einer
Spannungsquelle sowie einem Voltmeter. Die gemessene
Spannung entsteht am Spannungsteiler bestehend aus
R3, dem Innenwiderstand der Spannungsquelle und der
Parallelschaltung R1∥R2 des Innenwiderstandes R1 des
Spannungsmessers M1 sowie des zu prüfenden Widerstandes
R2
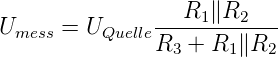 | (4.36) |
Aus Gleichung (4.35 folgt für die Parallelschaltung R1∥R2
der Widerstand
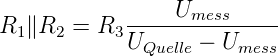 | (4.37) |
Hier ist das Resultat eine Spannungsdifferenz einer nicht
messbaren Quellspannung UQuelle und einem abgelesenen
Wert Umess: die Schaltung ist sehr fehlerbehaftet. Sie
sollte nur eingesetzt werden, wenn es nicht anders geht. Das
Resultat für Abb. 4.43 ist:
Vergleicht man den numerischen Wert dieses Resultates mit
den vorherigen Ergebnissen fällt die doch deutlich schlechtere
Genauigkeit auf.
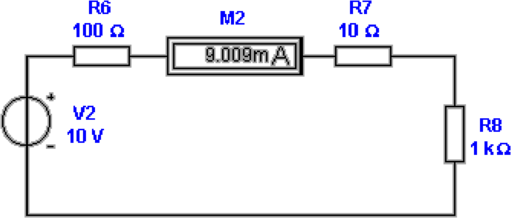
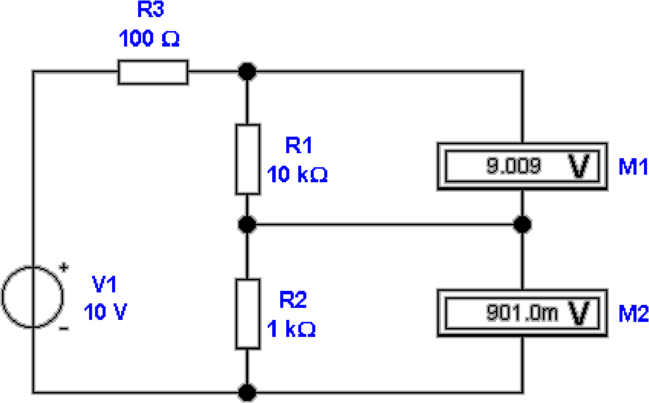
Besser ist die Schaltung nach Abb. 4.44. Hier wird, bei
bekannter Spannungsquelle der durch den Widerstand
fliessende Strom gemessen. Es gilt
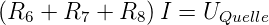 | (4.38) |
Damit wird der Wert des zu messenden Widerstandes
R8
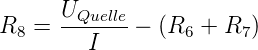 | (4.39) |
Die Innenwiderstände des Strommessers, R7 (gut bekannt),
und der Spannungsquelle, R6 (sehr schlecht bekannt), müssen
vom aus Spannung und Strom berechneten Wert abgezogen
werden. Das Resultat ist
Diese Schaltung ist wesentlich genauer als die mit
Spannungsmesser. Andererseits muss gefordert werden, dass
der Innenwiderstand der Spannungsquelle R6 sehr viel kleiner
als der zu messende Widerstand R8 ist.
Abbildung 4.45 zeigt eine ratiometrische Schaltung zur
Widerstandsmessung, wie sie bei digitalen Voltmetern
üblich ist. Unter der Annahme, dass der Innenwiderstand
der Spannungsmesser M1 und M2 Ri » R1,2 ist liefert
diese Schaltung hervorragende, von der Betriebsspannung
unabhängige Resultate. Trifft die Annahme nicht zu, so muss
mit R1,2∥Ri gerechnet werden. Der Widerstandswert von R2
wird so berechnet:
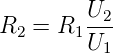 | (4.40) |
Dabei ist der gemessene Wert von R2 in sehr guter
Näherung unabhängig von R3 oder UQuelle. Als Resultat
erhält man mit den obigen Werten:
Wie Abbildung 4.46 zeigt wird diese Schaltung in vielen
Digitalvoltmetern verwendet.
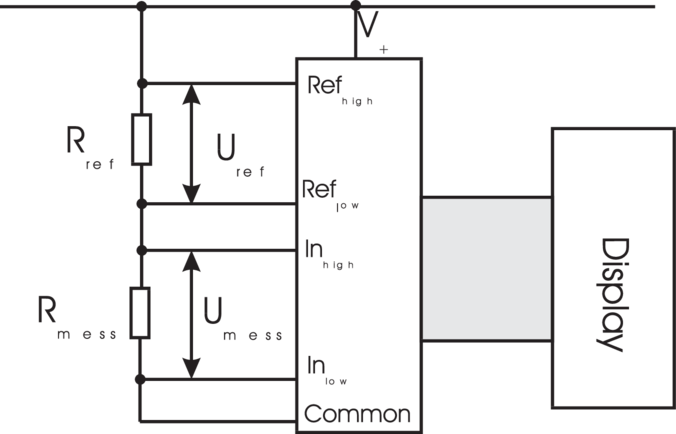
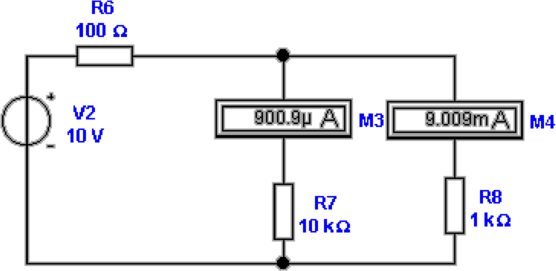
Abbildung 4.47 zeigt die ratiometrische Widerstandsmessung
mit Strömen. Unter der Annahme, dass der Innenwiderstand
der Strommesser M3 und M4 Ri «R7,8 sei werden direkt die
richtigen Widerstandswerte, sonst wird R7,8 + Ri gemessen.
Es gilt
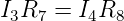 | (4.41) |
unabhängig von R3 oder UQuelle. Wir erhalten schliesslich
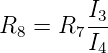 | (4.42) |
und eingesetzt den Wert
Die bisher vorgestellten Messmethoden sind für ganz kleine
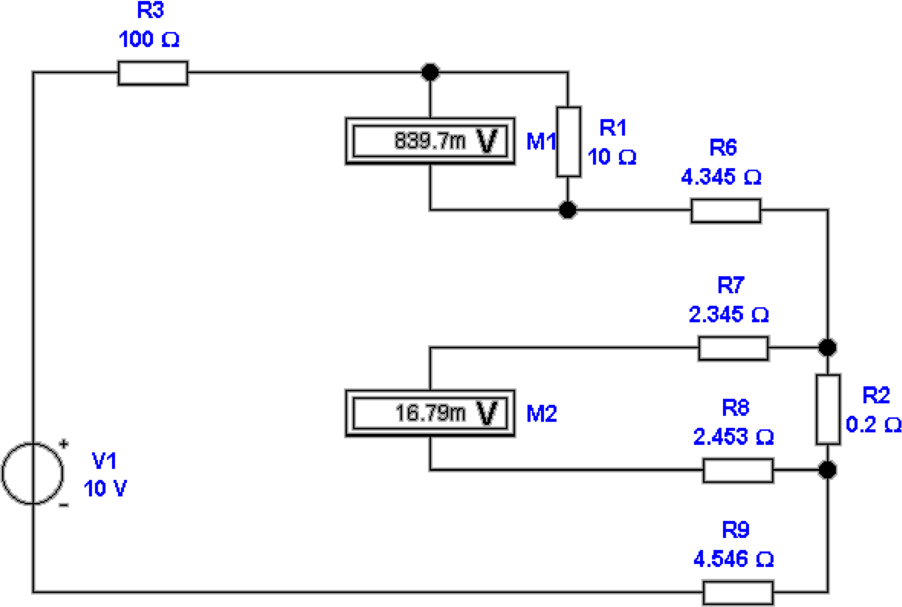
Widerstände nicht geeignet. Abbildung 4.48 zeigt die
Vierdraht-Methode zur Widerstandsmessung.
Eine Spannungsquelle wird über einen Referenzwiderstand
R1 und über Kabel mit den Widerständen R6 und R9 an
den zu messenden Widerstand R2 angelegt. Um den
Spannungsabfall in R − 6 und R9 zu kompensieren, wird die
Spannung am Widerstand direkt abgegriffen und über die
Widerstände R7 und R8 zum Spannungsmesser gebracht.
Wenn der Innenwiderstand von M1 und M2 sehr viel
grösser als die anderen beteiligten Widerstände sind,
dann hat man eine analoge Messmethode wie in Abb.
4.45. In diesem Falle sind die Kabelwiderstände und die
Übergangswiderstände nicht relevant. Wir erhalten für
R2
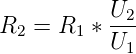 | (4.43) |
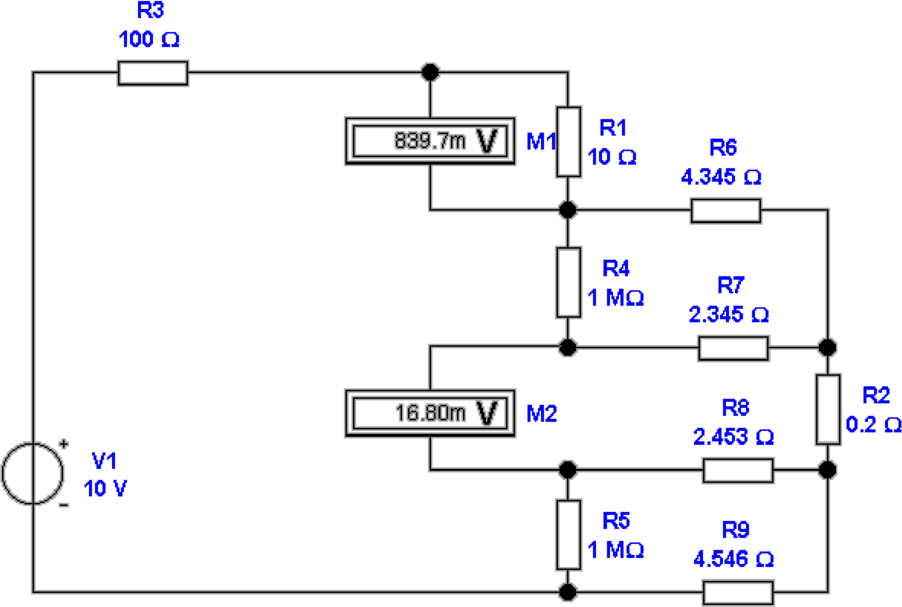
Die Widerstände R4 und R5 in Abbildung 4.49 ermöglichen
eine automatische Umschaltung von der 2-Draht- zur
4-Draht-Methode. Sie sind aber auch die Ursache für
zusätzliche Fehler. Mit der Nebenbedingung:
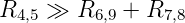 | (4.44) |
oder
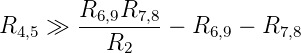 | (4.45) |
können deren Widerstandswerte vernachlässigt werden. Wir
erhalten dann wie ohen R4 und R5
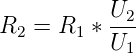 | (4.46) |
Ist man sicher, dass der Spannungsabfall in den
Widerständen R6 und R9 nicht wesentlich über 0.1V
ansteigt, könne man die Widerstände durch jeweils eine oder
zwei in Durchlassrichtung geschaltete Dioden ersetzen.
Die durch R4 und R5 hervorgerufenen Spannungsfehler
sind:
Die beiden oben gezeigten Schaltungen sind ideal zu
Messung kleiner Widerstände geeignet. Sie haben jedoch
einen gravierenden Nachteil: je kleiner die Widerstände
sind, desto höher werden sie thermisch belastet. Dies
liegt daran, dass zur Messung eines Spannungsabfalls ein
minimaler Wert benötigt wird. Für R →∞ gilt
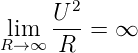 | (4.51) |
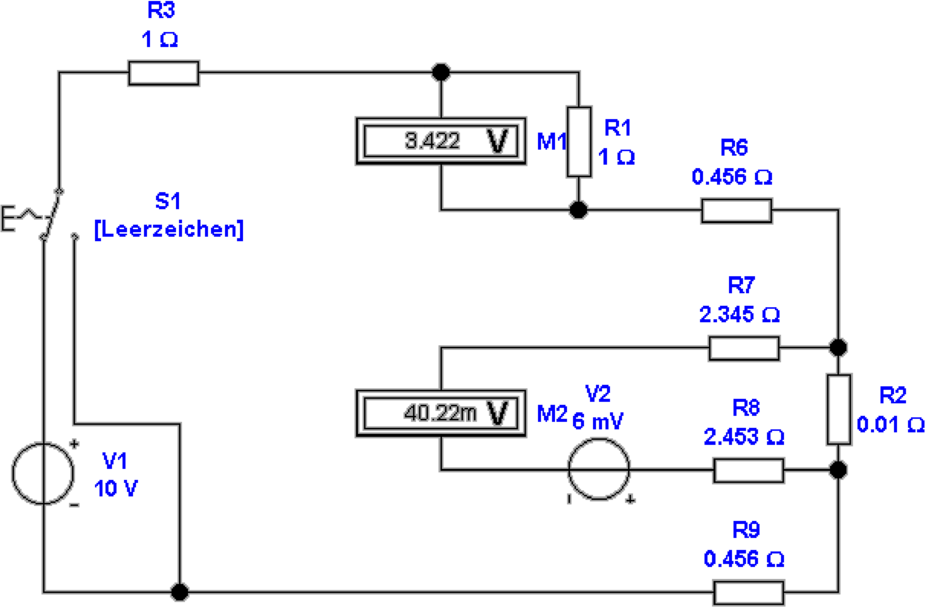
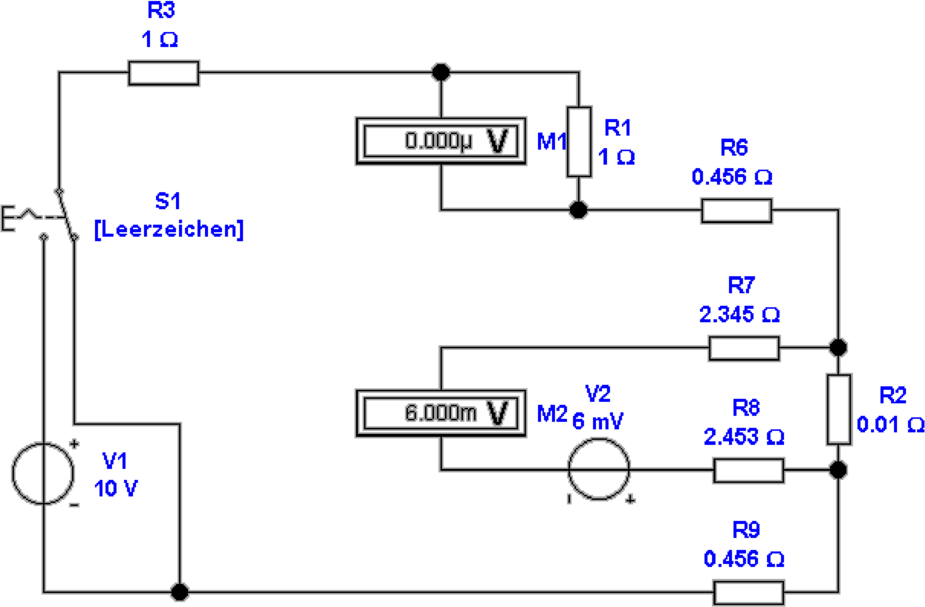
Abbildung 4.50 zeigt, wie mit einer gepulsten Messung das
Problem der zu grossen thermischen Belastung umgangen
werden kann. Wir nehmen hier an, dass die Spannungsquelle
V 2 (6 mV) die durch thermische Belastung hervorgerufenen
Spannungen zusammenfasst. Auf der linken Seite wird die
Schaltung mit eingeschalteter Messspannungsquelle gezeigt,
rechts ist die Messspannungsquelle ausgeschaltet. Indem die
Messspannungsquelle nur den Bruchteil 𝜀 der gesamten
Messzeit eingeschaltet wird wird die Verlustleistung an
R2
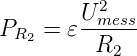 | (4.52) |
Zusätzlich kann man, wenn die Messpannungsquelle mit der
Frequenz ν geschaltet wird, Lock-In-Verstärker verwenden
und so die Empfindlichkeit steigern und die thermische
Belastung senken. Im oberen Teil, bei eingeschalteter
Messspannungsquelle gilt
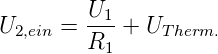 | (4.53) |
Im unteren Teil, ohne Messspannungsquelle hat man
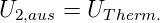 | (4.54) |
Den gesuchten Widerstand R2 findet man mit
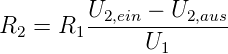 | (4.55) |
Sollte dem Widerstand
R2
jedoch grosse kapazitive oder, wahrscheinlicher,
induktive Komponenten parallel geschaltet sein,
ist die Messung nicht mehr zuverlässig.
4.1.6 Messung von L und C
Die Messungen von Kapazitäten und Induktivitäten kann auf
verschiedene Arten erfolgen:
- Messung der Zeitkonstanten bei Einschalt- oder
Ausschaltvorgängen.
- Messung von Resonanzfrequenzen in Schwingkreisen
- Messung der komplexen Impedanzen.
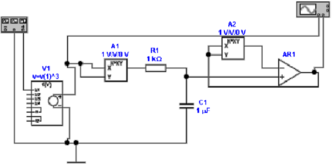
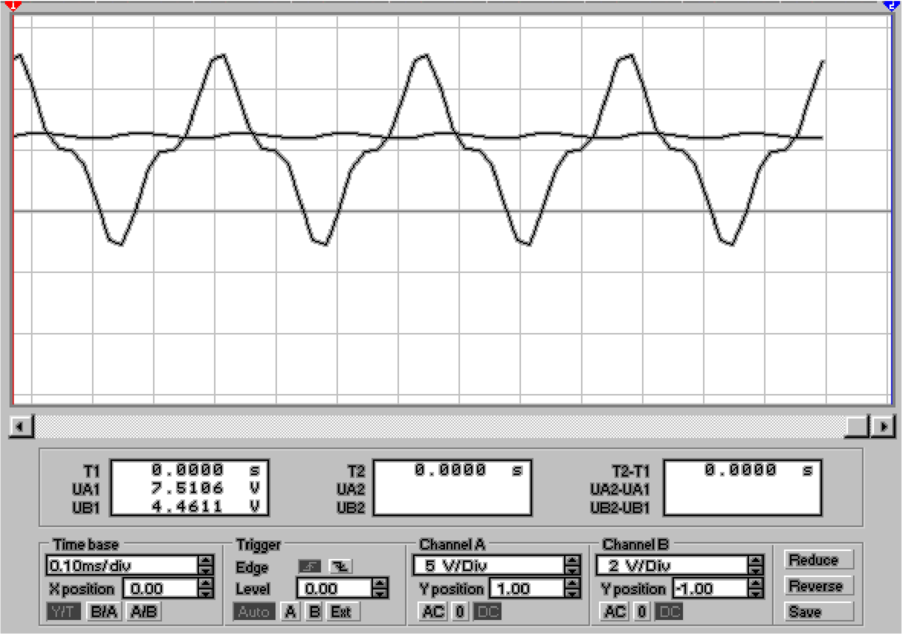
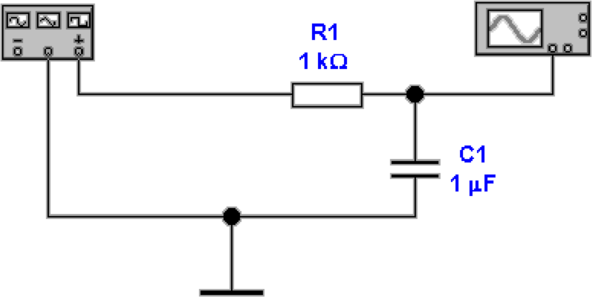
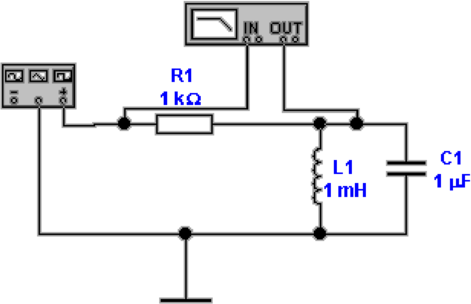
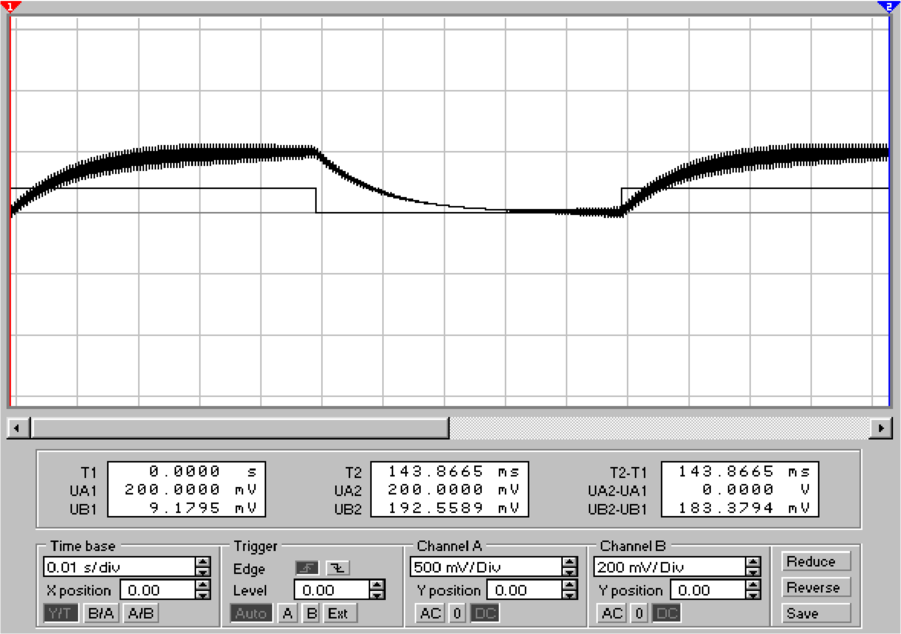
In Abbildung 4.51 wird eine Kapazität C1mit einer
periodischen Wechselspannung über einen Widerstand R1
geladen und entladen. Im Entladefall hat man, dass
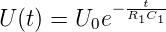 | (4.56) |
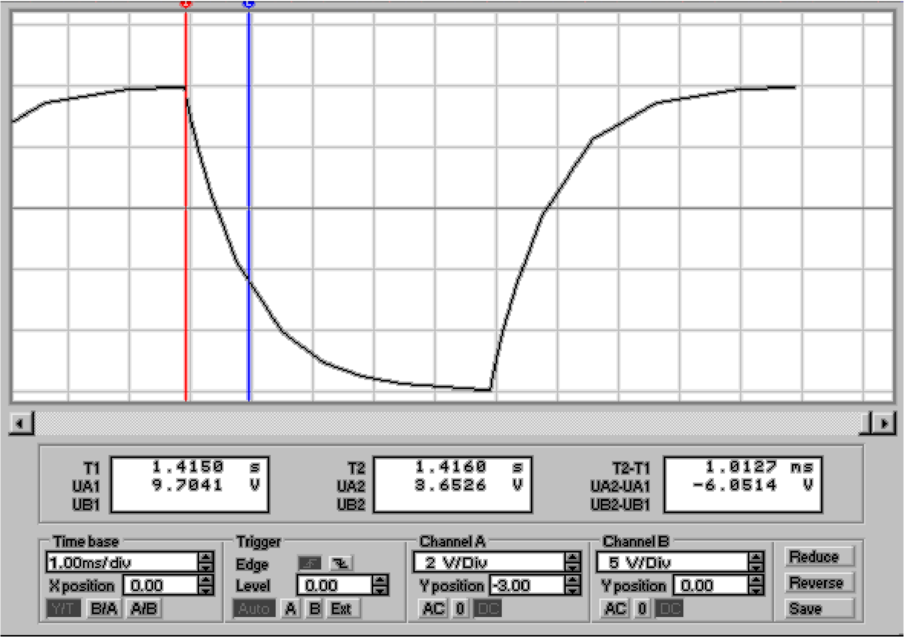
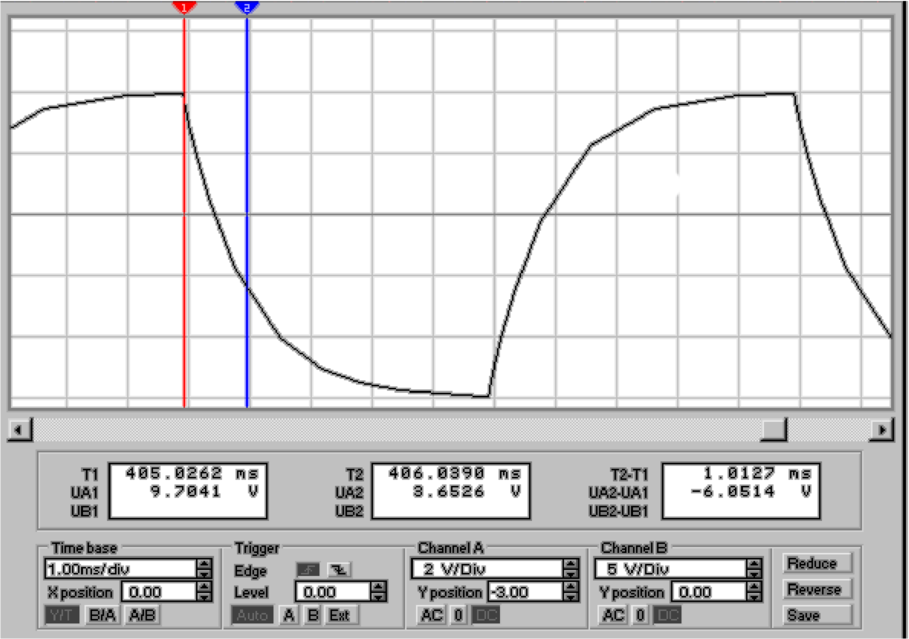
Nun ist bei t = τ = R1C1 die Spannung gerade
U(τ) = U0 ∗e−1 = 0.3679U
0. Aus der Zeitkonstante für
Entladung in Abb. 4.51, rechts, (Differenz zwischen blauer
und roter Markierung) liest man ab, dass τ = 1.0127ms ist.
Daraus folgt mit R1 = 1kΩ dass C1 = 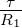 =
= 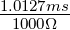 = 1.0127μF
ist. Man ersieht aus der kurzen Rechnung, dass eine genau
Messung Schwierigkeiten bieten dürfte.
= 1.0127μF
ist. Man ersieht aus der kurzen Rechnung, dass eine genau
Messung Schwierigkeiten bieten dürfte.
Für die Anstiegszeit gilt
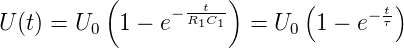 | (4.57) |
d.h. man rechnet analog zum Entladefall. Hier ist
angenommen worden, dass die Spannung U0 zwischen 0V und
ihrem (positiven) Maximalwert hin- und hergeschaltet wird.
ist die untere Spannung nicht null, muss ihr Wert als Offset
abgezogen werden.
In Abbildung 4.51 wird über eine Induktivität L1 an
den Widerstand R1 eine periodischen Rechteckspannung
angelegt. Wenn die Eingangsspannung von U0 0 wechselt hat
man
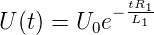 | (4.58) |
Nun ist bei t = τ = 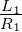 die Spannung gerade
U(τ) = U0 ∗e−1 = 0.3679U
0. Aus der Zeitkonstante für
Entladung in Abb. 4.51, rechts, (Differenz zwischen blauer und
roter Markierung) liest man ab, dass τ = 1.0368ms ist. Daraus
folgt mit R1 = 1Ω dass L1 = τR1 = 1.0368ms1Ω = 1.0368mH
ist. Man ersieht auch aus der kurzen Rechnung, dass eine
genau Messung Schwierigkeiten bieten dürfte.
die Spannung gerade
U(τ) = U0 ∗e−1 = 0.3679U
0. Aus der Zeitkonstante für
Entladung in Abb. 4.51, rechts, (Differenz zwischen blauer und
roter Markierung) liest man ab, dass τ = 1.0368ms ist. Daraus
folgt mit R1 = 1Ω dass L1 = τR1 = 1.0368ms1Ω = 1.0368mH
ist. Man ersieht auch aus der kurzen Rechnung, dass eine
genau Messung Schwierigkeiten bieten dürfte.
Für die Anstiegszeit gilt analog
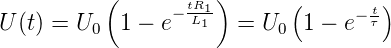 | (4.59) |
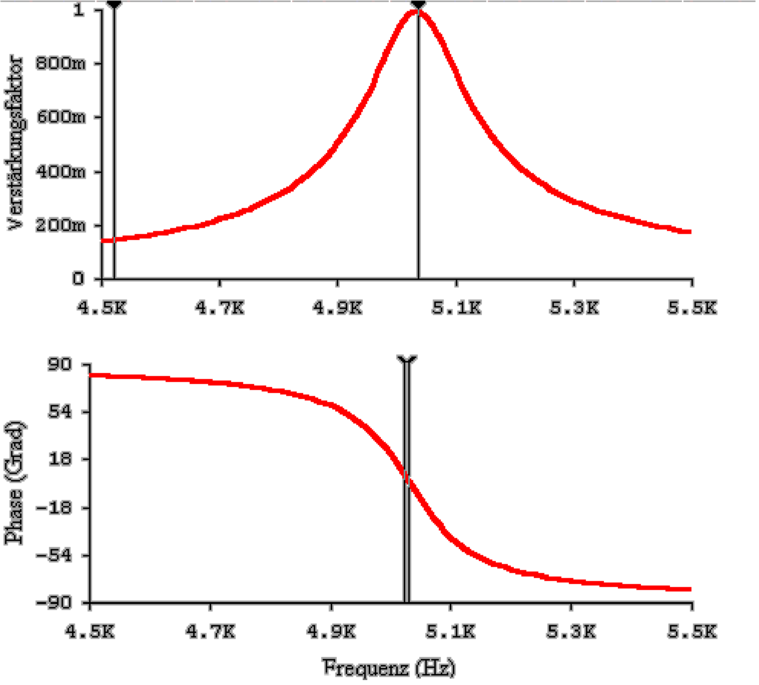
Abb. 4.53 zeigt, wie man mit einem Schwingkreis Kapazitäten
oder Induktivitäten bestimmen kann. Für einen Schwingkreis
gilt allgemein:
dabei ist ω0 die Resonanzfrequenz und Q die Güte
des Schwingkreises. In der Phase α(ω) gilt in unserem
Falle
Damit ist die Resonanzfrequenz und die Güte einfach aus
dem Phasenbild ablesbar.
Der Amplitudengang hat zwar prinzipiell die
gleiche Aussagekraft wie der Phasengang, ist
aber wesentlich ungenauer auszumessen. Eine fast
immer gültige Regel besagt: Resonanzfrequenz
ω0 und Güte Q bestimmt man aus der
Phase.
Die letzte Möglichkeit, die Werte von Kapazitäten und
Induktivitäten zu bestimmen, ist mit ihren komplexen
Impedanzen zu rechnen.
In den im Abschnitt 4.1.5 besprochenen Schaltungen wird
die Gleichspannung durch eine Wechselspannung mit
bekannter Amplitude U und Frequenz ω ersetzt. Der so
bestimmte Impedanzwert Z kann dann umgerechnet werden
nach
4.1.7 Brückenschaltungen
Mit Brückenschaltungen kann man komplexe Impedanzen
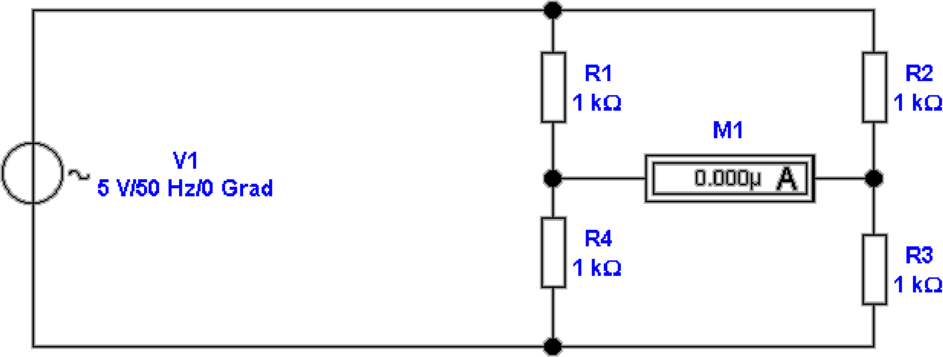
sehr schnell und genau vermessen. Abbildung 4.54 zeigt
eine Widerstandsbrückenschaltung. Im Idealfall erhält
man für das Widerstandsverhältnis im abgeglichenen
Falle
Für die unabgeglichene Brücke erhält man:
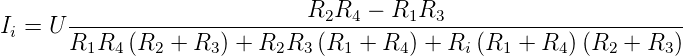 | (4.67) |
Die Herleitung von Gleichung (4.67) finden Sie im Anhang
B.
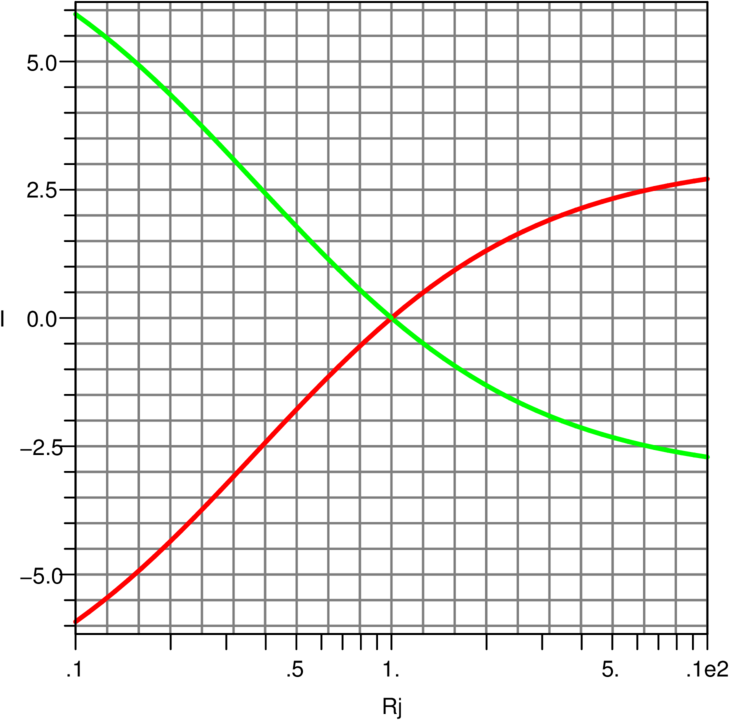
Abbildung 4.55 zeigt die Änderung des Querstromes
in der Brücke als Funktion der Änderung der einzelnen
Teilwiderstände. Sehr schön ist aus dieser Darstellung
ersichtlich, dass die Ausgangsspannung der Brücke nichtlinear
ist.
Die Grösse des Querstromes hängt nicht nur vom
Ungleichgewicht der Brücke ab, sondern auch vom
Innenwiderstand des Strommessers zum Nullabgleich.
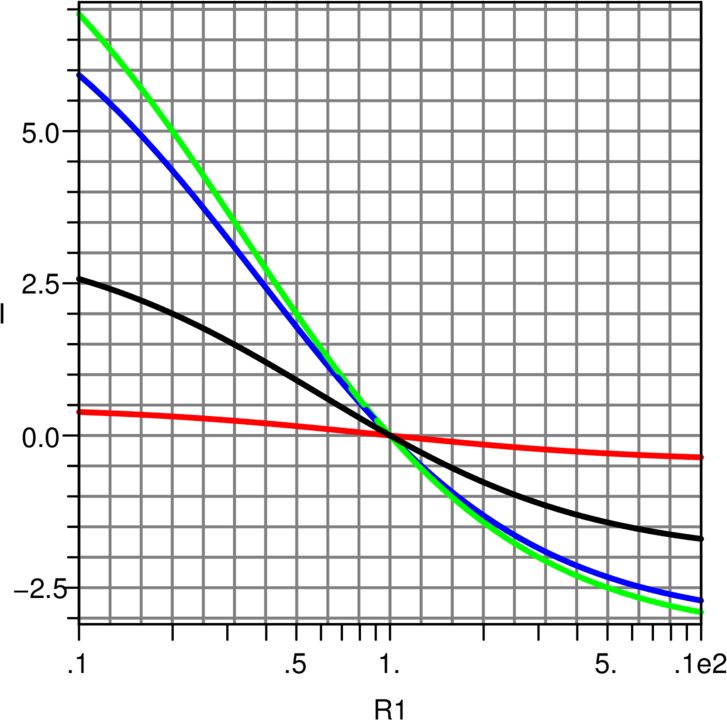
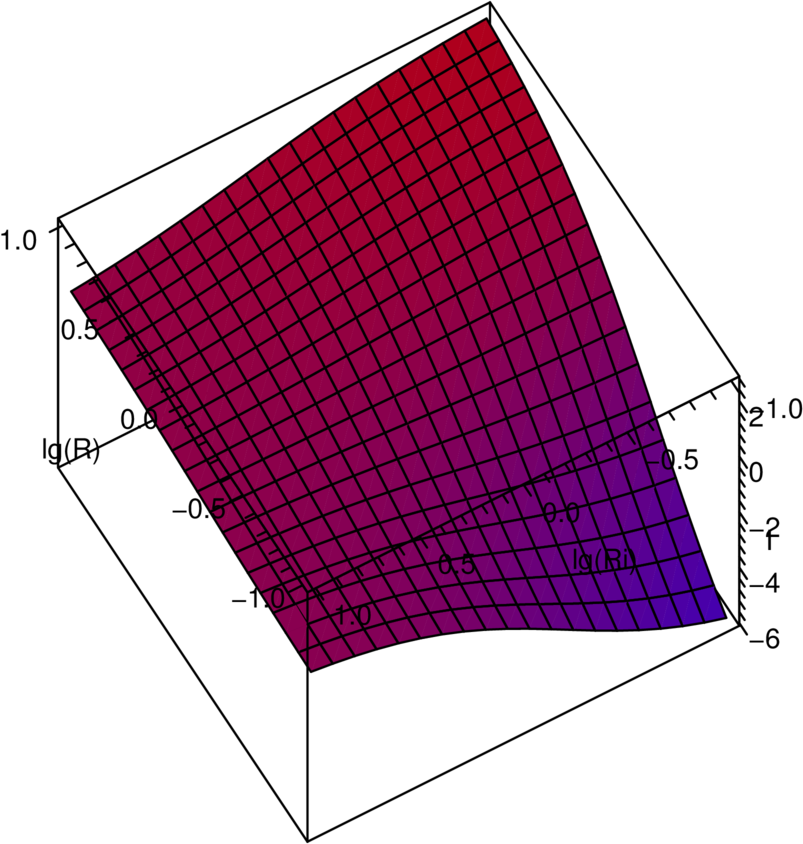
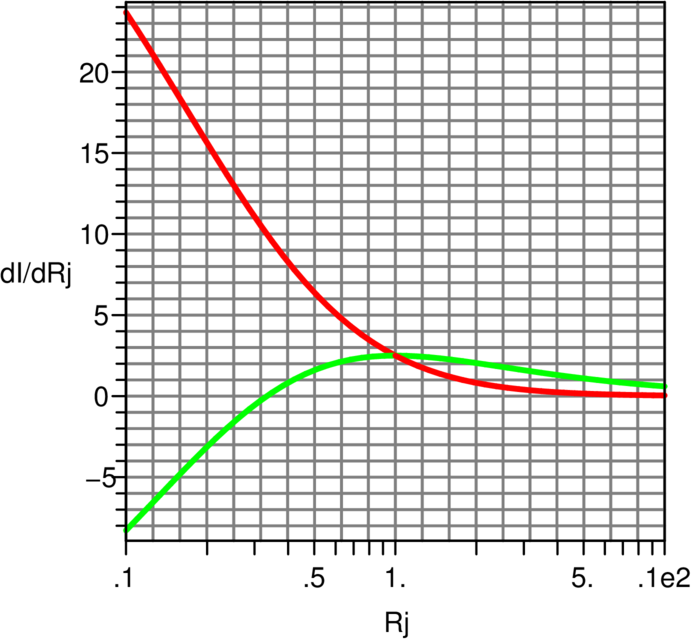
Abbildung 4.56 zeigt den Einfluss des Innenwiderstandes auf
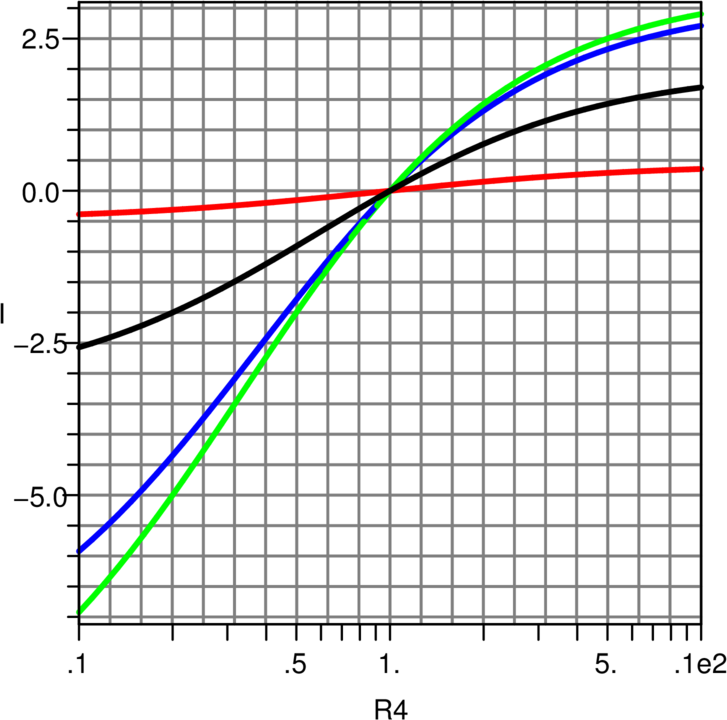
die Ausgangskurve, wenn R1 variiert wird. Analog dazu zeigt
Abbildung 4.57 den Einfluss des Innenwiderstandes auf die
Ausgangskurve, wenn R4 variiert wird.
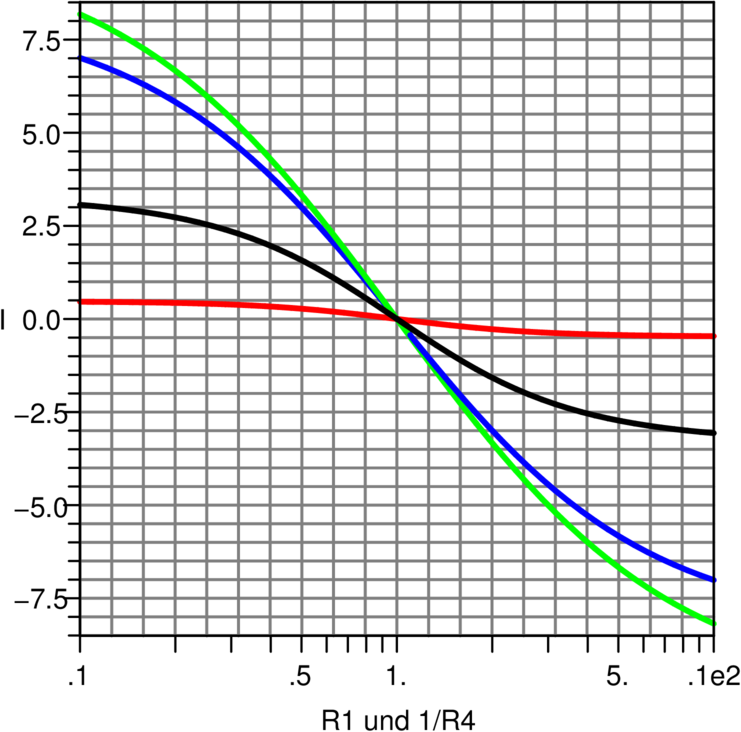
Interessant ist der Fall, wo R1 und R4 gegengleich sich
ändern, wo also R4 = 1∕R1 gilt. Dieser Fall ist bei Sensoren
wie Dehnungsmessstreifen oder piezoresistive AFM-Cantilever
gegeben. Da variieren beide Widerstände in einem
Brückenzweig. Abbildung 4.58 zeigt die Ausgangskurven.
Es ist bemerkenswert, um wieviel linearer das Signal
ist.
Für den Fall dass der Innenwiderstand des Strommessers
Ri = 0 ist, erhält man die vereinfachte Gleichung:
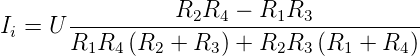 | (4.68) |
Misst man die Brückenspannung, so ergibt sich aus
Gleichung 4.67
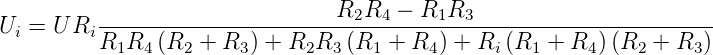 | (4.69) |
Weiter sieht man, dass für Ri →∞
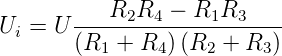 | (4.70) |
ist. Abbildung 4.59 fasst den Einfluss des Innenwiderstandes
nochmals zusammen.
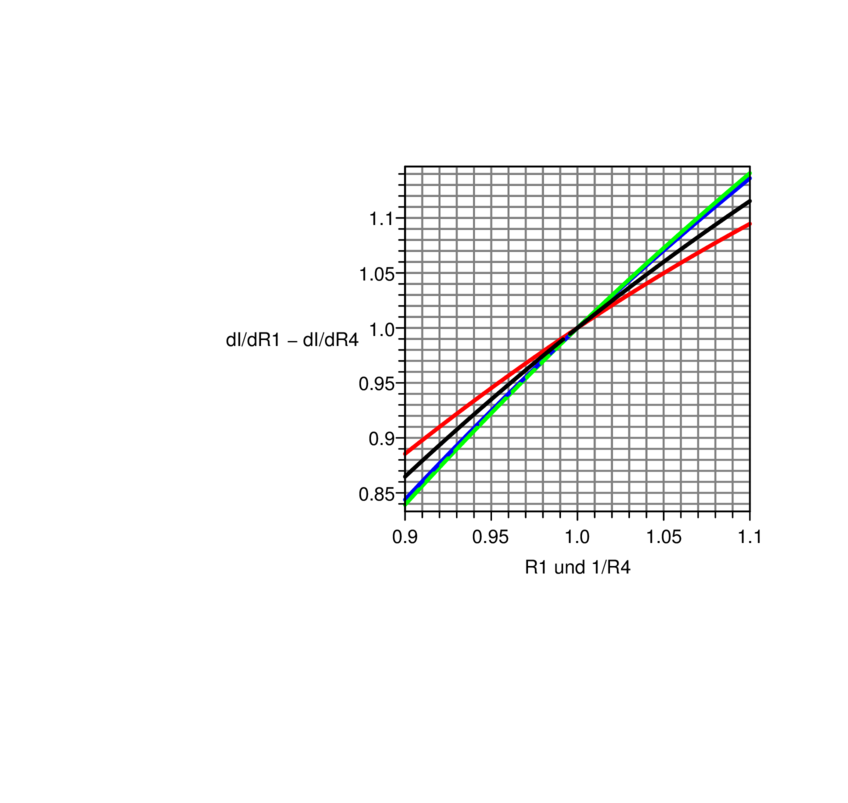
Die Empfindlichkeit auf Veränderungen von R1 oder R4
ergibt sich aus
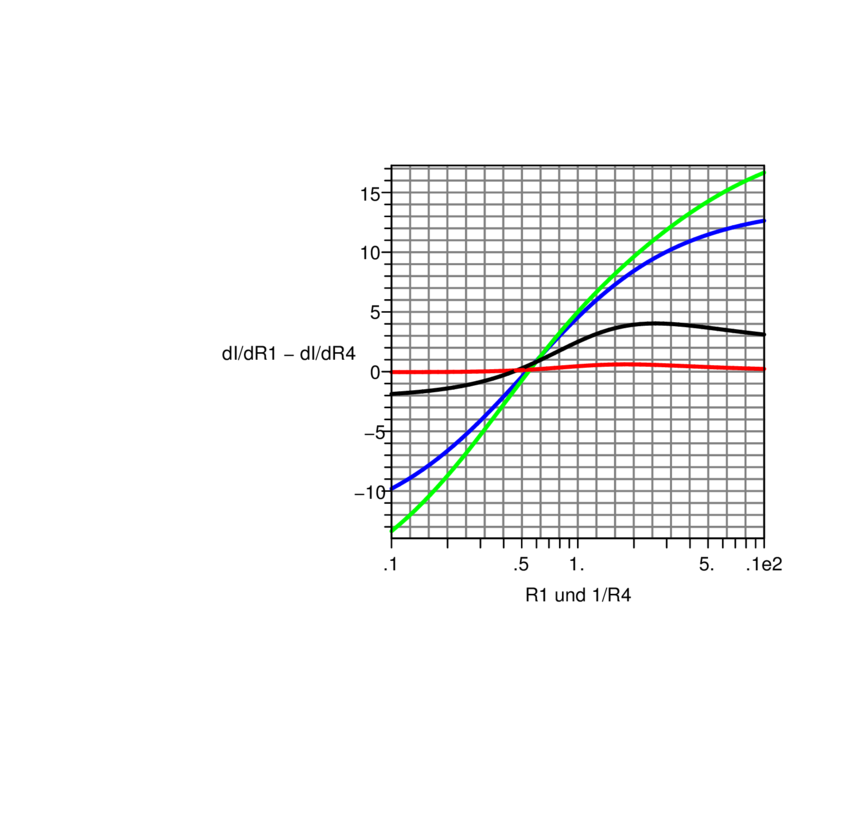
Abbildung 4.60 vergleicht dabei die Variation von R1 und
R4. Die Steigungen ändern sich extrem, das heisst, dass der
lineare Bereich doch stark eingeschränkt ist.
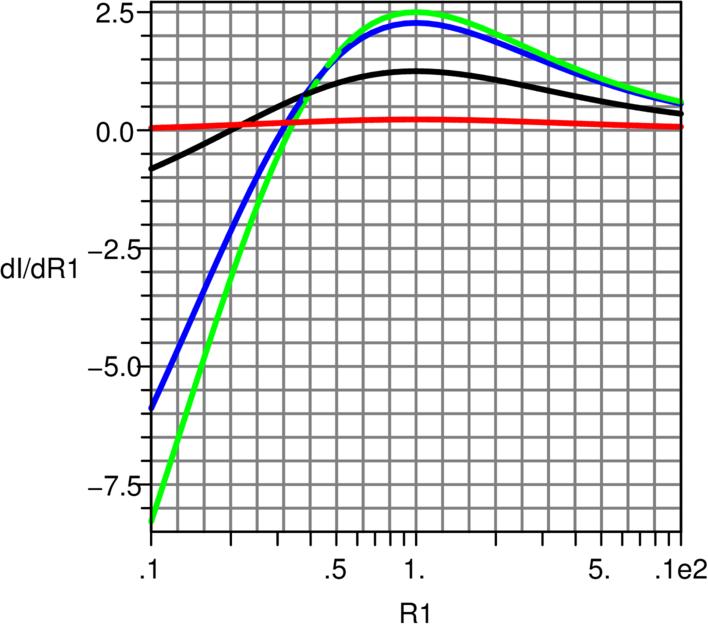
Abbildung 4.61 zeigt den Einfluss des Innenwiderstandes
Ri, wenn R1 sich ändert. Die Empfindlichkeit der Brücke
nimmt mit steigendem Innenwiderstand ab.
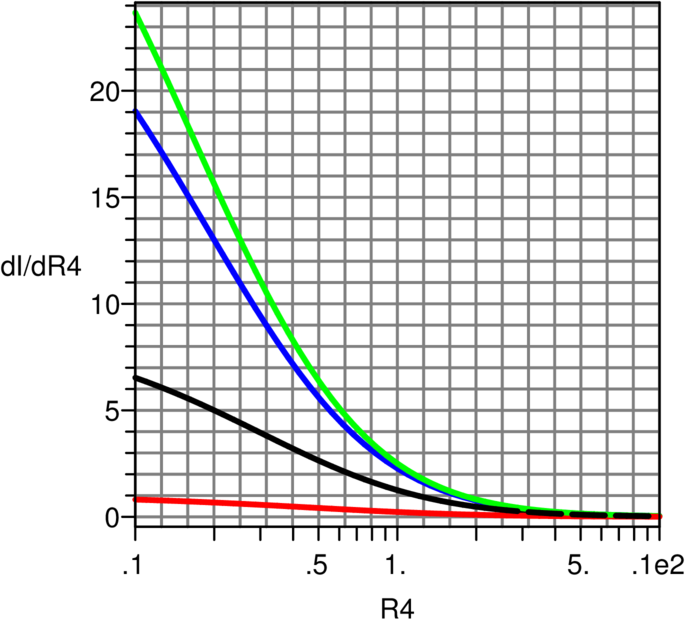
Abbildung 4.62 zeigt den Einfluss des Innenwiderstandes
Ri, wenn R4 sich ändert. Die Empfindlichkeit der Brücke
nimmt mit steigendem Innenwiderstand ab.
Wenn sich R1 und R4 = 1∕R1 gegengleich ändern,
dann variiert die Empfindlichkeit wie in Abbildung 4.63
angegeben.
Eine Detaildarstellung der normierten Empfindlichkeit in
Abbildung 4.64 zeigt, dass für grosse Innenwiderstände Ri die
Empfindlichkeit am wenigsten variiert. Die Messkurve kann
mit guter Näherung als linear mit einem kleinen paraboloiden
Korrekturterm angesehen werden.
Für den Fall dass der Innenwiderstand des Strommessers
Ri = 0 ist, erhält man die vereinfachte Gleichung:
Die Empfindlichkeit für Spannungsmessungen ist
Schliesslich erhält man für Ri →∞
Die Aussagen über die Empfindlichkeit für die Strommessung
gelten auch für die Spannungsmessung. Ein möglichst
lineares Ausgangssignal benötigt hohe Querwiderstände
Ri: Spannungsmessungen sind für nicht abgeglichene
Brücken vorzuziehen.
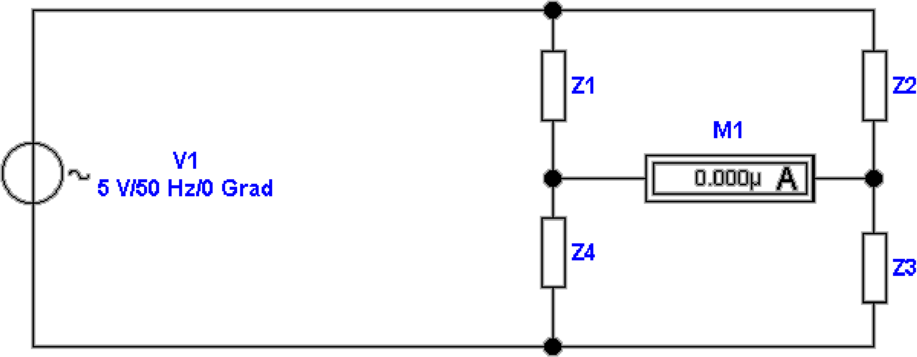
Die Gleichungen für die Wheatstone-Brücke für allgemeine
Impedanzen (Abb. 4.65 können aus Gleichung (4.66)
abgeleitet werden. Folgende Ersetzungen sind vorzunehmen:
Gleichung wird dann zu
Daraus ist ersichtlich, dass eine Brücke nur abgleichbar ist,
wenn sowohl die Beträge wie auch die Phasen abgeglichen
sind. Diese Bedingungen sind:
4.1.8 Wandlerschaltungen
Wandlerschaltungen werden benötigt, um digitale mit
analogen Schaltkreisen zu verbinden. Während digitale
Darstellungen von Signalen prinzipiell mit beliebiger
Genauigkeit machbar sind, limitiert das Rauschen von
analogen Schaltkreisen (siehe auch Abschnitt 2.8.1). Da
Analog-Digitalwandler auf Digital-Analog-Wandlern aufbauen
werden zuerst diese beschrieben.
4.1.8.1. Digital/Analog-Wandler
Die Ausgangsspannung eines Digital/Analog-Wandlers ist
prinzipiell wertdiskret. Bei sehr kleinen Diskretisierungsschritten
kann das Rauschen von analogen Bauteilen diese
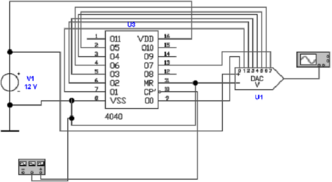
Spannungsschritte maskieren. Abbildung 4.66 zeigt die
prinzipielle Schaltung sowie die Ausgangskurven. Ein 4040
CMOS-Zähler U3 gespiesen vom Funktionsgenerator zählt
von 000 nach FFF. Die untersten acht Bit werden in den
generischen, idealen Digital-Analog-Wandler U1 gespiesen.
Seine Ausgangsspannung wird in der Mitte und unten
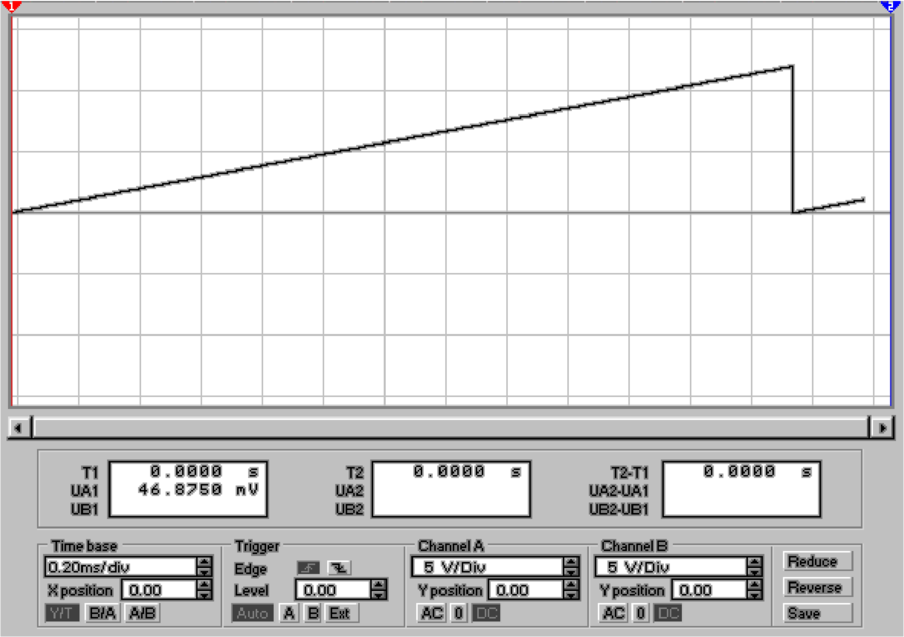
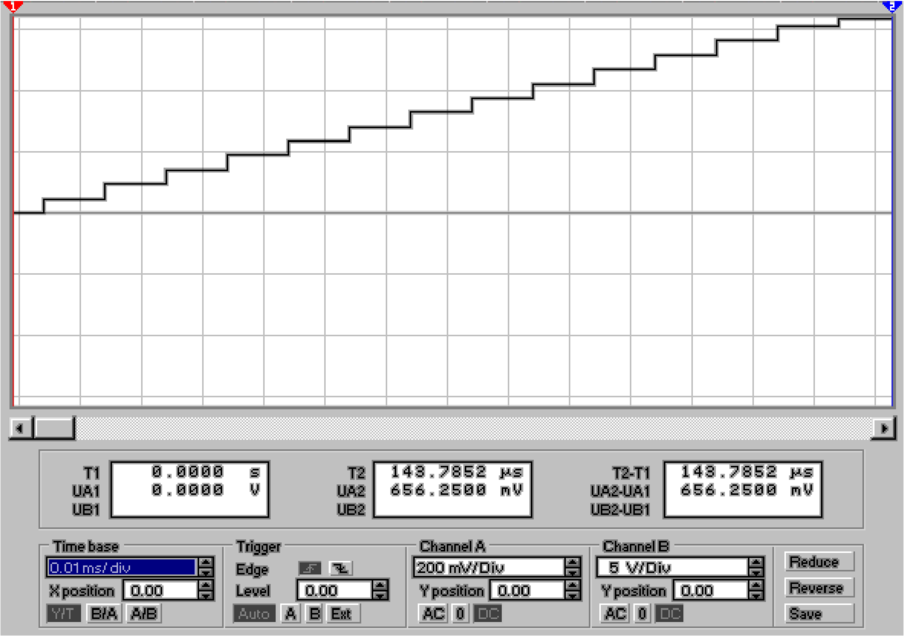
in Abb. 4.66 gezeigt. Die mittlere Abbildung zeigt die
Ausgangsrampe. Um die Stufenhöhe auflösen zu können,
ist ein Teil der Messkurve in der unteren Darstellung
vergrösstert. Sehr schön sind die einzelnen Stufen im
Ausgangssignal zu sehen. da dies ein idealer Wandler ist, sind
die Stufen im gleichen Abstand.
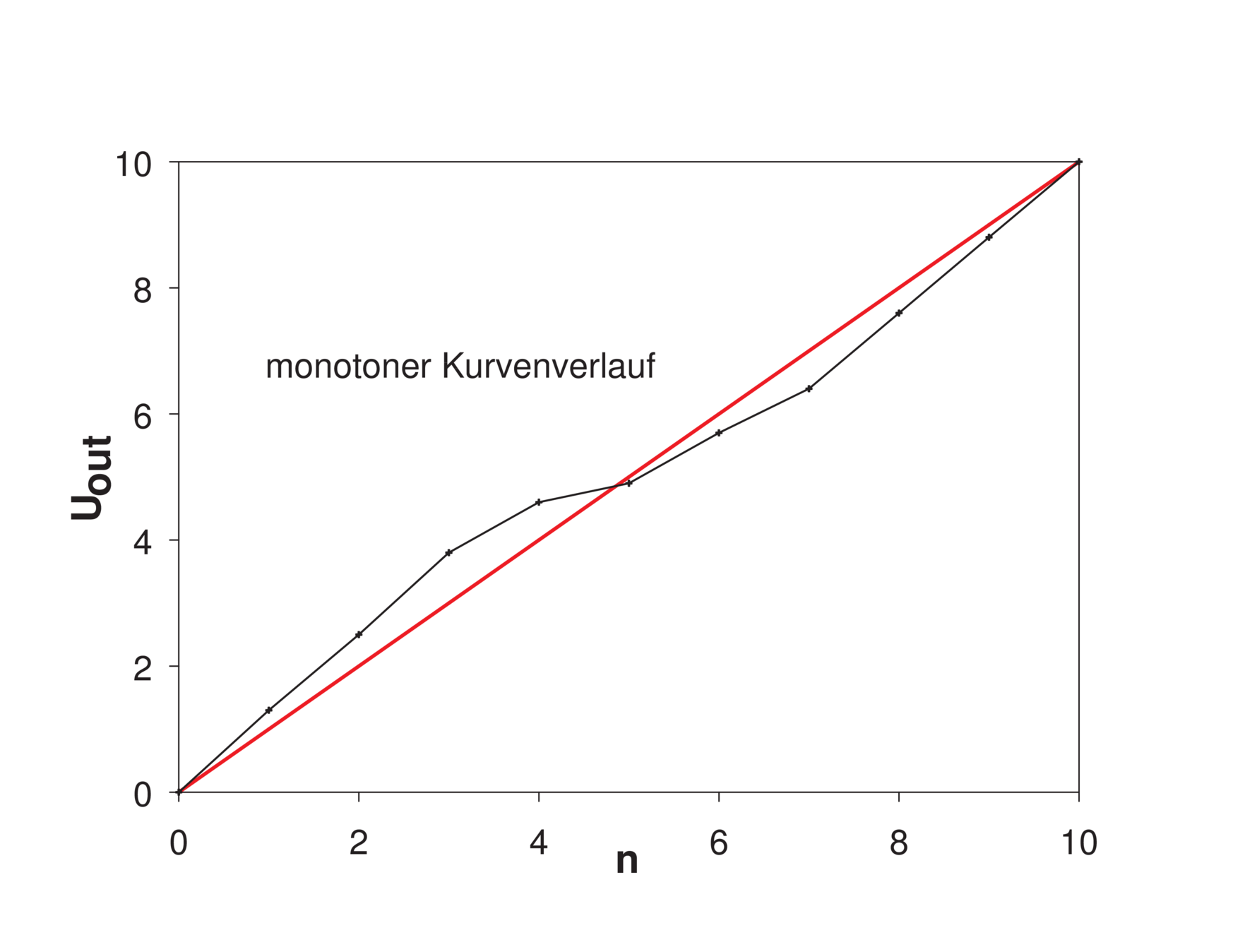
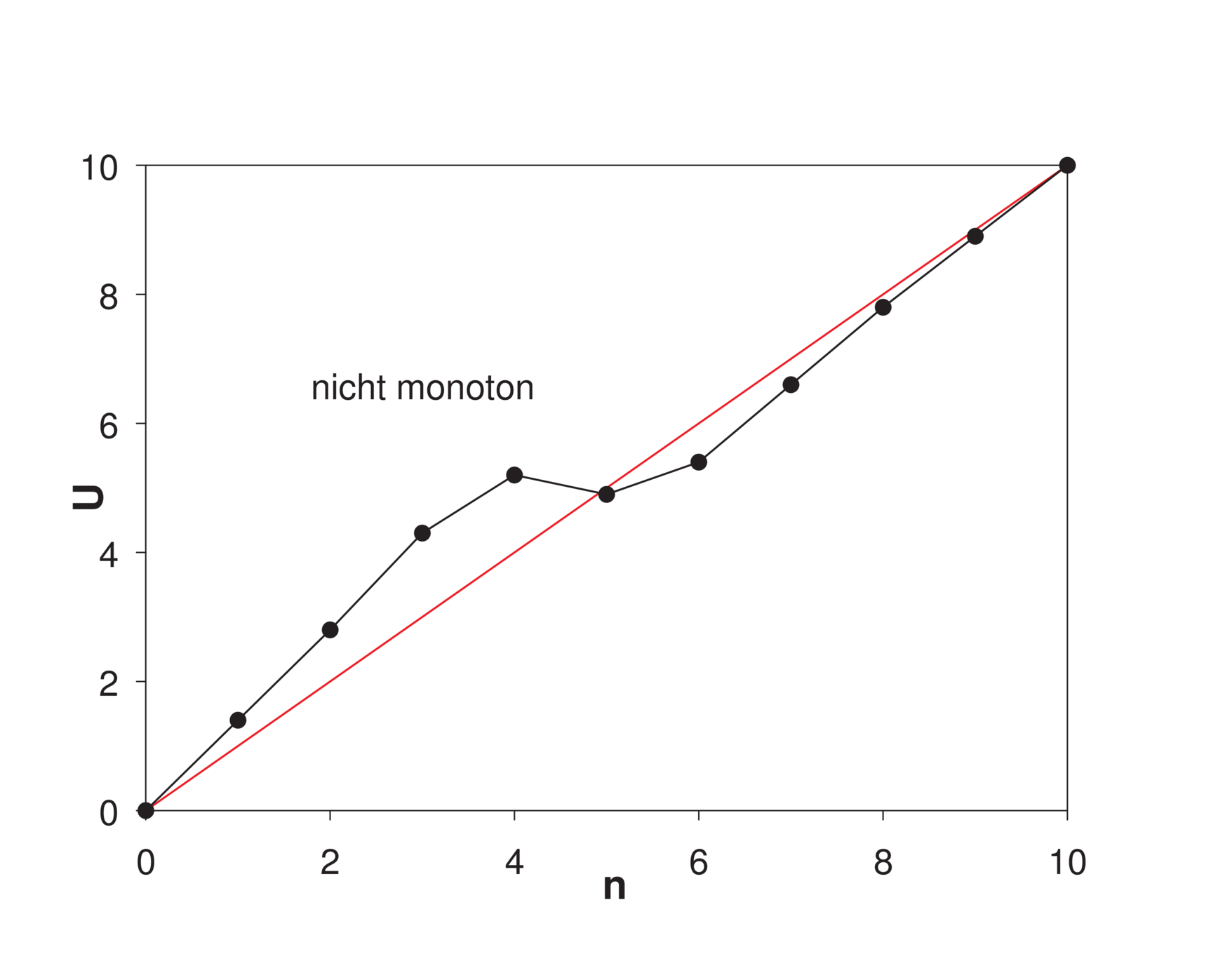
Digital-Analogwandler haben die folgenden Fehler:
- Die Stufenhöhe ist nicht konstant. Beide Kurven in
in Abb. 4.67 zeigen diesen Fehler.
- Die Ausgangsspannung ist keine monotone Funktion
der Eingangsspannung. Die rechte Kurve in Abb 4.67
ist nicht monoton.
|
|
|
|
|
| Zahl | Ausgang | Fehler | angepasste | Fehler |
| Zahl | DAC | durch Endpunkte | Gerade | angep. Gerade |
|
|
|
|
|
| 0 | 0 | 0 | 0,44 | 0,44 |
| 1 | 1,3 | -0,3 | 1,36 | 0,06 |
| 2 | 2,5 | -0,5 | 2,28 | -0,22 |
| 3 | 3,8 | -0,8 | 3,2 | -0,6 |
| 4 | 4,6 | -0,6 | 4,12 | -0,48 |
| 5 | 4,9 | 0,1 | 5,04 | 0,14 |
| 6 | 5,7 | 0,3 | 5,96 | 0,26 |
| 7 | 6,4 | 0,6 | 6,88 | 0,48 |
| 8 | 7,6 | 0,4 | 7,8 | 0,2 |
| 9 | 8,8 | 0,2 | 8,72 | -0,08 |
| 10 | 10 | 0 | 9,64 | -0,36 |
|
|
|
|
|
| |
| Tabelle 4.2.: | Tabelle
der Ausgangswerte von Digital-Analog-Wandlern. Die
erste Spalte zeigt die Zahlenwerte. Die zweite Spalte die
Ausgangswerte des Wandlers. In der dritten Spalte werden
die Fehler angegeben, bezogen auf eine Gerade durch die
Endpunkte. Die vierte Spalte zeigt die Ausgangsgerade
U = 0.44 + 0.92n. Die letzte Spalte zeigt die Fehler dazu. |
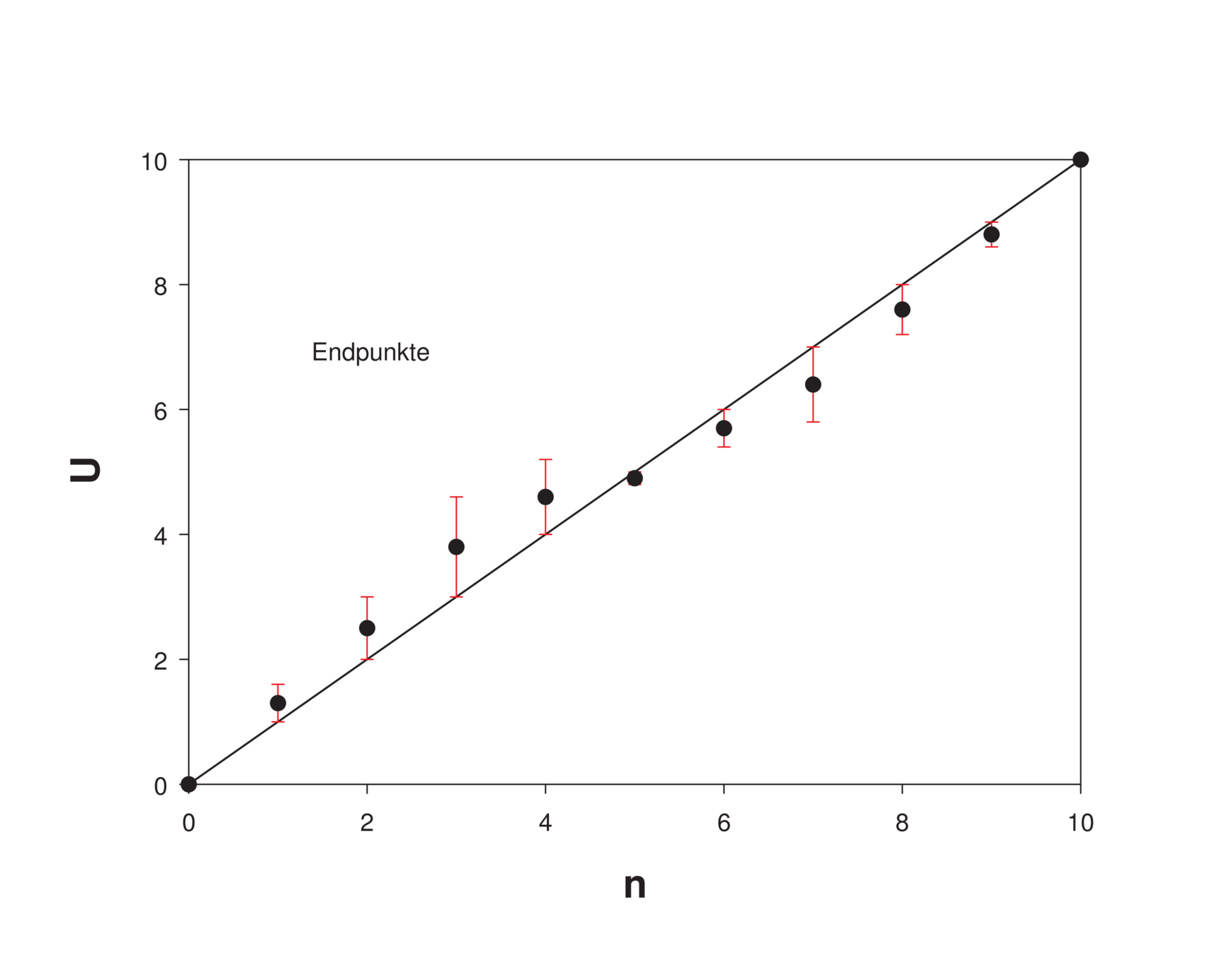
Die Grösse der Bitfehler kann auf zwei Arten bestimmt
werden. Einerseits kann, wie in Abb. 4.68, linke Seite, eine
Gerade durch die Endpunkte als Referenz verwendet
werden. Die daraus resultierenden Fehler werden in
Tabelle 4.2 in der zweiten und dritten Spalte aufgelistet.
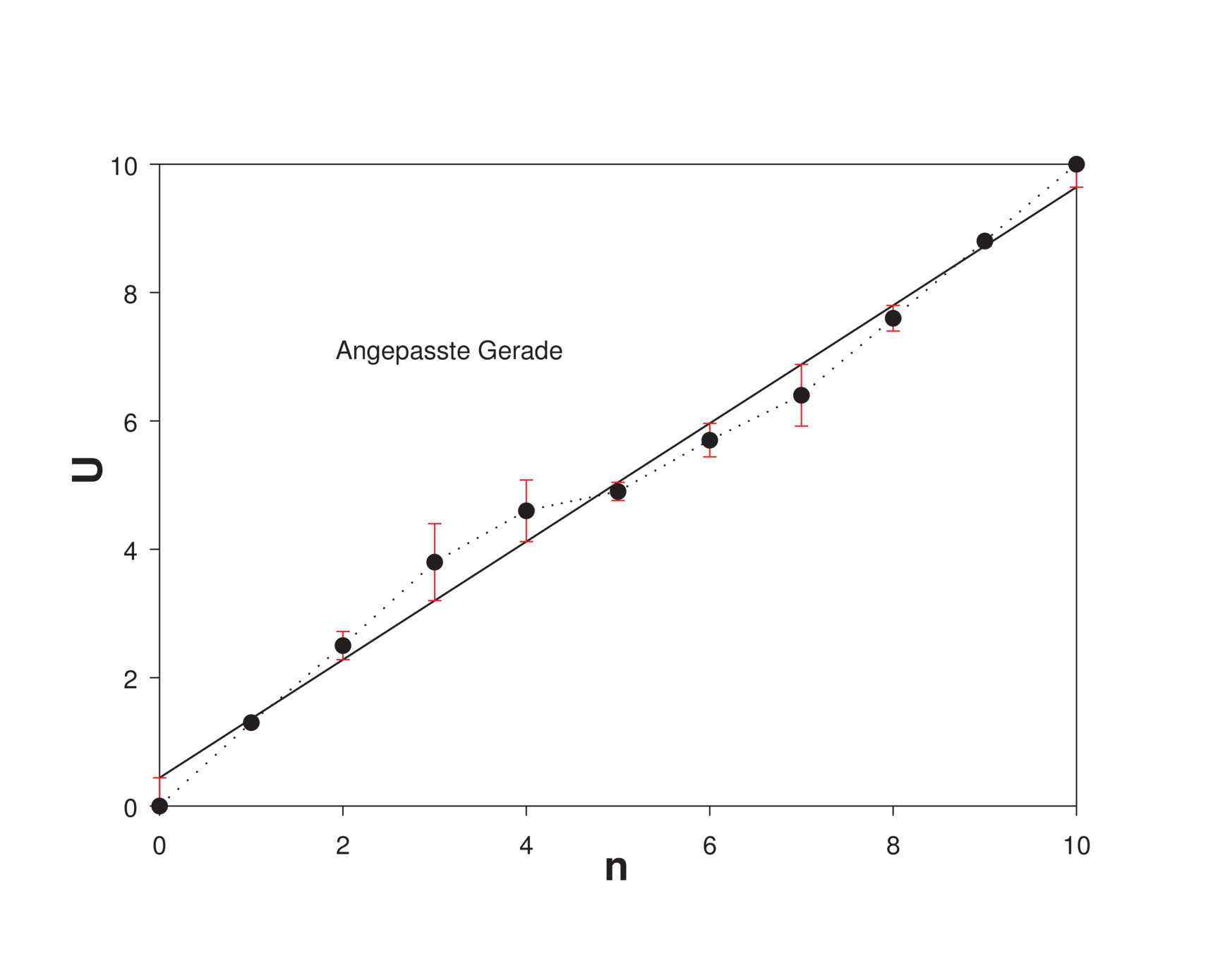
Andererseits kann eine durch Regression bestimmte Gerade
als Referenz dienen (Abb. 4.68, rechts, und Tabelle
4.2, Spalten 4 und 5). Die so berechneten Fehler sind
kleiner .
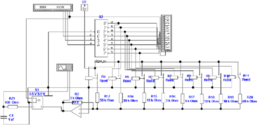
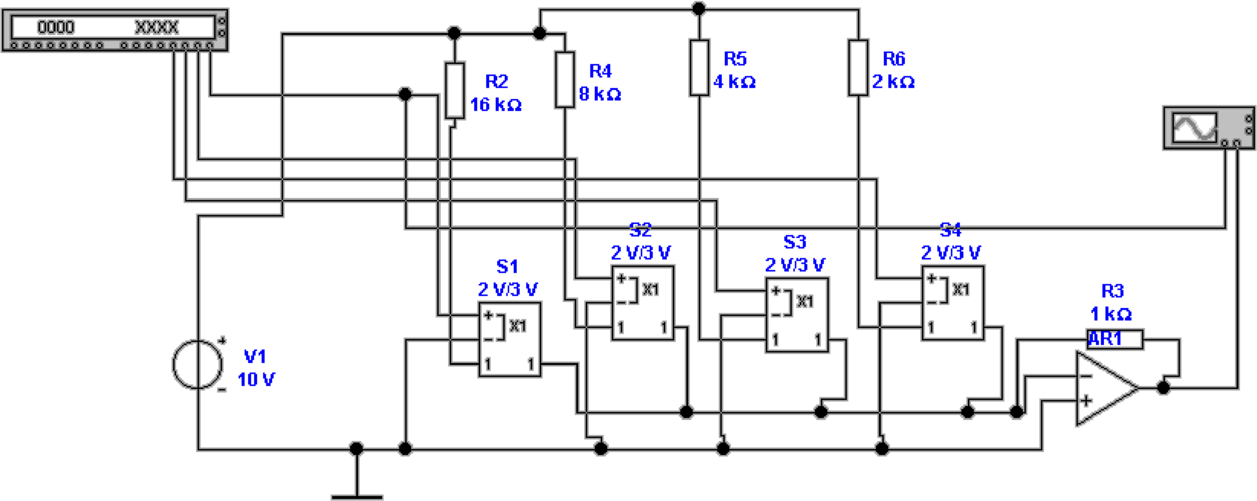
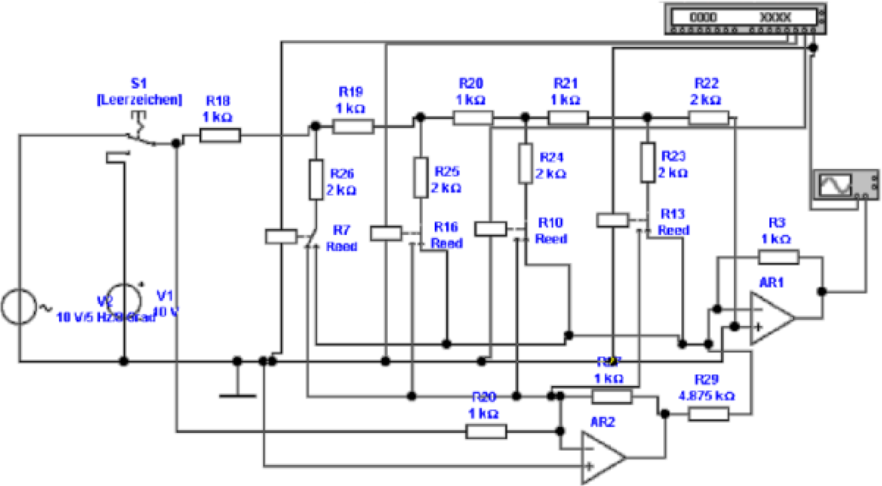
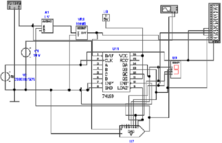
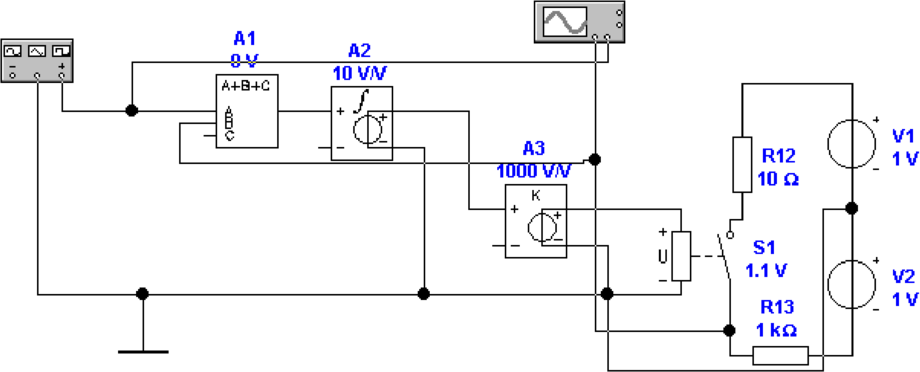
Direkte D/A-Wandler
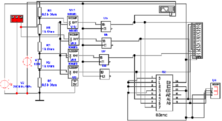
Direkte Digital-Analog-Wandler setzen jede Zahlenkombination
am Eingang in einen mit einem diskreten Widerstand (hier
R12, R14-R20) kodierten Wert um. Die Abbildung 4.69 zeigt
eine mögliche Implementierung.
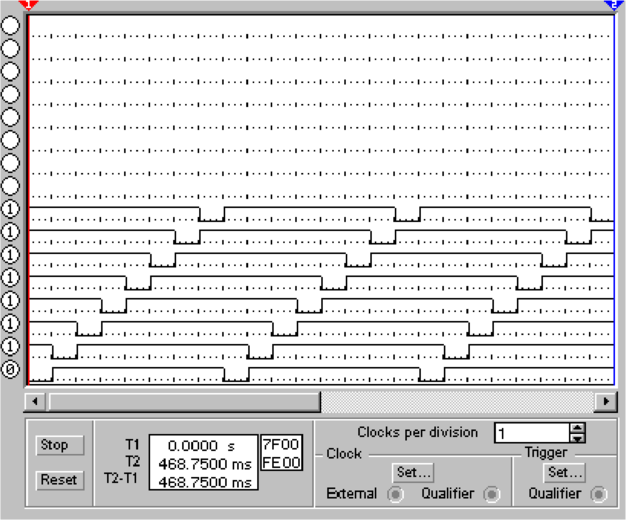
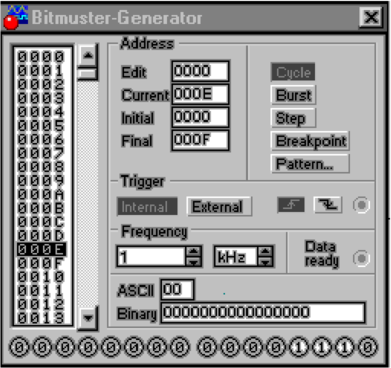
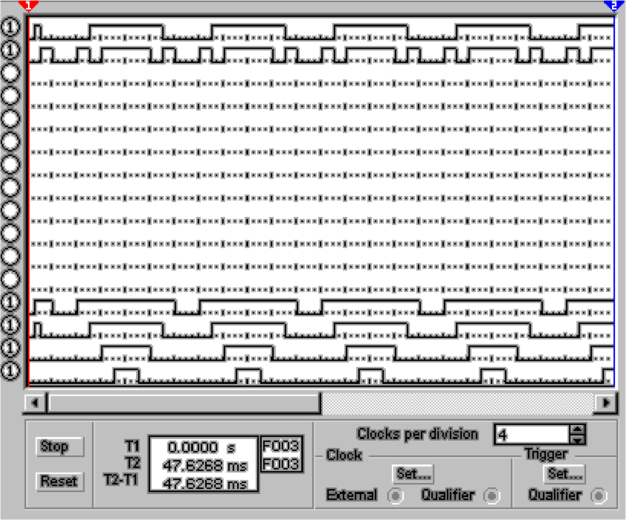
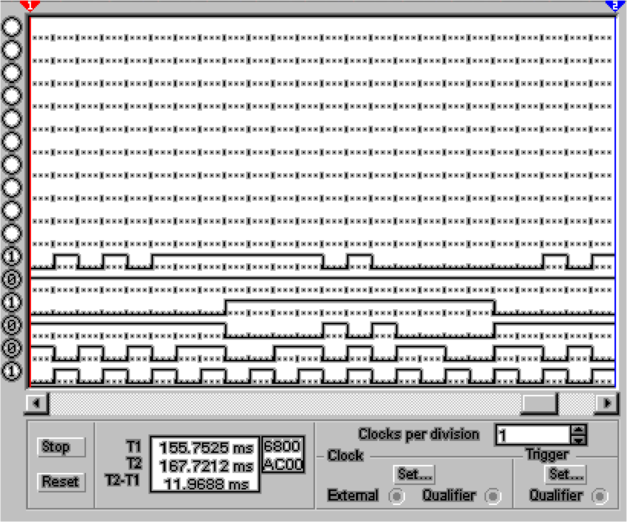
Mit einem Bitmustergenerator werden die Zahlen von 0H
bis FH generiert. Das niederwertigste Bit dient dabei als
Taktgenerator.Der Demultiplexer U2 set eine 3-Bit-Zahl
(0-7) in acht Ausgänge um, die je einzeln auf dem
0-Pegel liegen. Dies ist aus dem Logik-Analysator (Abb.
4.69, unten links) ersichtlich. Die einzelnen Ausgänge
des Demultiplexers steuern einzelne Relais an, die die
individuell programmierbaren Widerstände R12, R14 −R20
einzeln mit der Referenzspannung U3 versorgen. Der
Operationsverstärker AR1 summiert die Stromwerte auf.
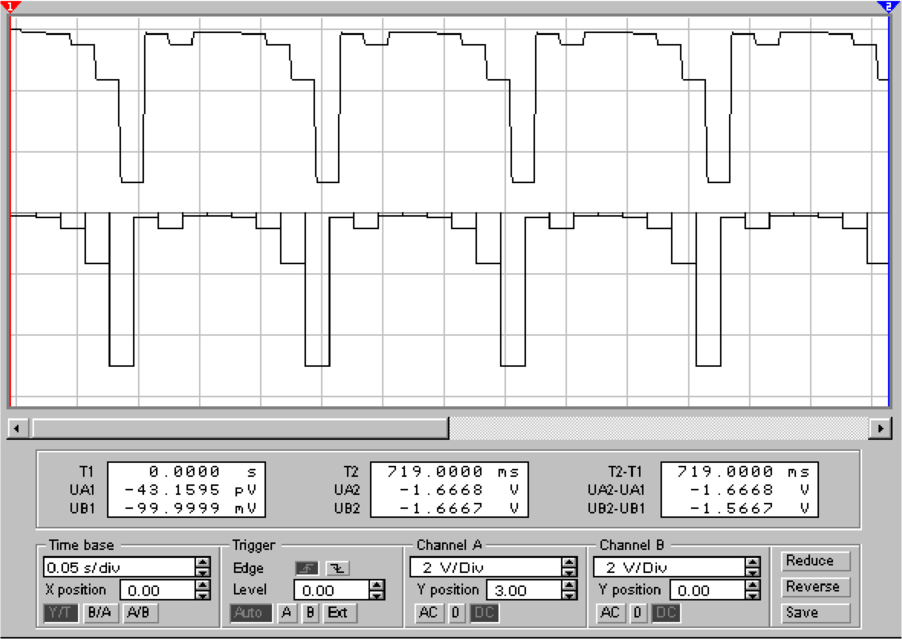
Am Eingang Y2 des Oszilloskopes, (Abb. 4.69, unten
rechts) sieht man, dass Spannungssprünge auftreten.
Dies kann verhindert werden, indem eine sogenannte
Deglitcher-Schaltung nachgeschaltet wird. Sie besteht hier
aus einem Analog-Schalter S1, dem mit R21 und C1 ein
Tiefpassglied nachgeschaltet ist. Dieses Tiefpassglied dient als
Analogspeicher und speichert während der Glitch-Phase
das Signal zwischen. Die Schaltung, bestehend aus S1,
R21 und C1 wird auch Sample&Hold-Schaltung oder
Abtast-Halte-Glied genannt.
Die direkte Wandlung von digitalen zu analogen Signalen
kann sehr schnell sein, bedingt aber einen enormen Aufwand
an Widerständen und vor allem, Schaltern.
Stromwägeverfahren
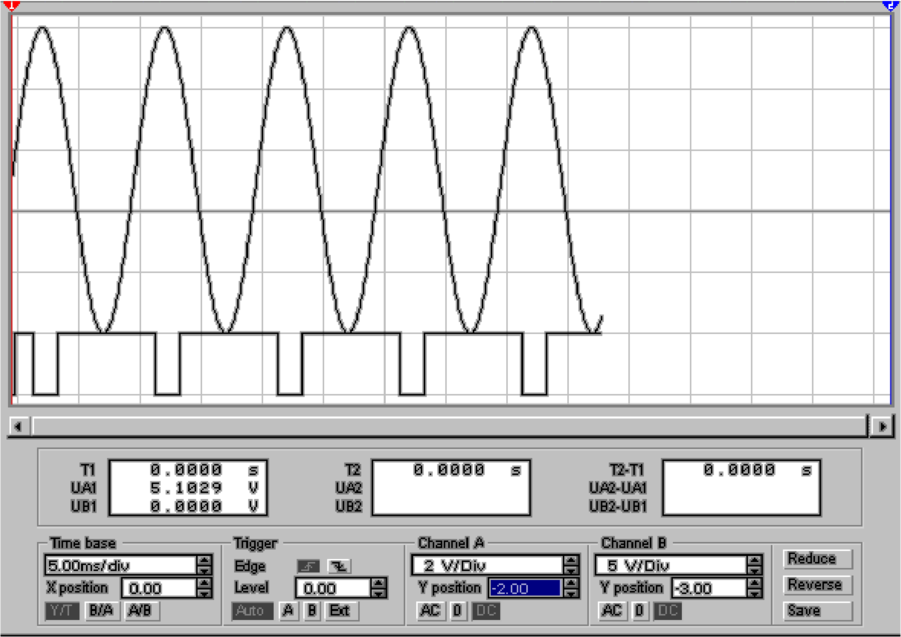
Das Stromwägeverfahren, wie es in Abbildung 4.70 gezeigt
wird, ist eine sehr viel effizientere Möglichkeit, digitale
Zahlenwerte in Spannungen umzuwandeln. Anders als beim
direkten Verfahren (Absatz 4.1.8.1.1) können jedoch
die Ausgangswerte pro Bit nicht unabhängig gewählt
werden.
In Abbildung 4.70 ist ein 4-Bit Digital-Analog-Wandler
gezeigt. Die Analogschalter S1 bis S4 verbinden die Widerstände
R2, R4 bis R6 mit dem als Strom-Spannungsschalter
geschalteten Operationsverstärker. Der Referenzwiderstand ist
hier R1 = 1kΩ. Wenn wir den Referenzwiderstand mit Rref
und den Widerstand für das m-te Bit (0 ≤m < n bei einem
n-Bit-Wandler) dann gilt
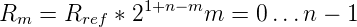 | (4.83) |
Hier ist n die Bitzahl des Wandlers, n − 1 ist das
höchstwertige Bit und 0 das niederwertigste Bit.
Damit die Spannungsänderung von Bit 0 nicht in der
mangelnden Genauigkeit von Bit m untergeht, muss für die
Widerstandstoleranz gelten:
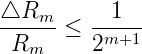 | (4.84) |
Bei einem 8-Bit Wandler bedeutet dies eine Genauigkeit
des kleinsten Widerstandes (grössten Leitwertes)
von  = 0.4%. Bei einem 12-Bit Wandler muss die
Genauigkeit
= 0.4%. Bei einem 12-Bit Wandler muss die
Genauigkeit 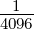 = 0.024% sein, bei einem 16-Bit
Wandler
= 0.024% sein, bei einem 16-Bit
Wandler
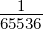 = 0.0015% sein. Dies sind illusorische Genauigkeiten, die
nur mit verheerend grossen Kosten erreichbar wären.
= 0.0015% sein. Dies sind illusorische Genauigkeiten, die
nur mit verheerend grossen Kosten erreichbar wären.
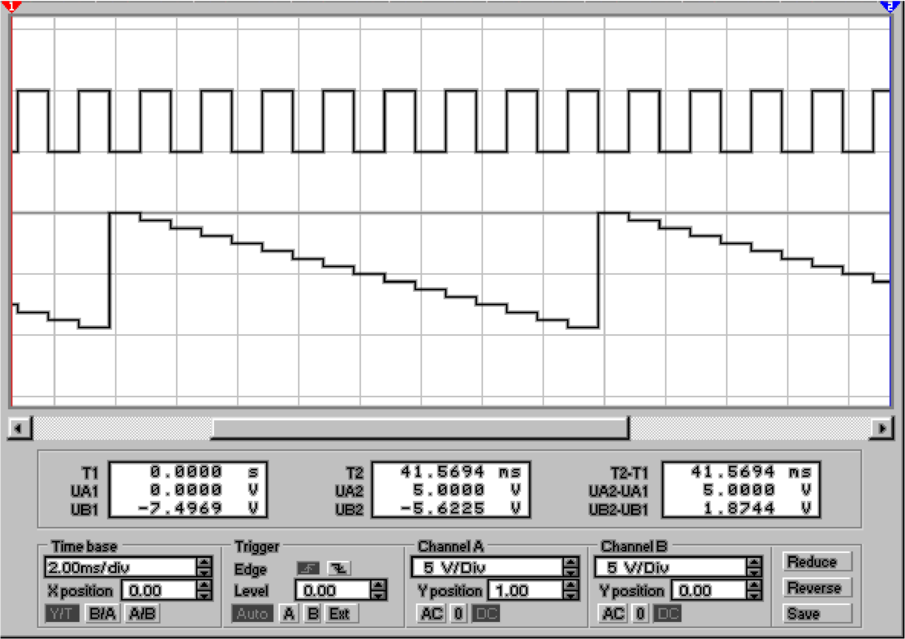
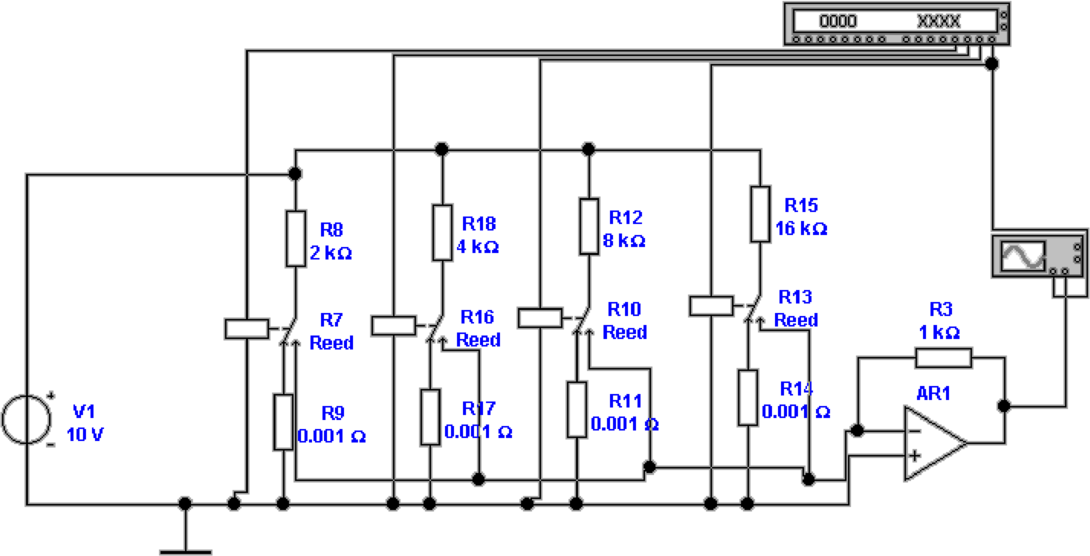
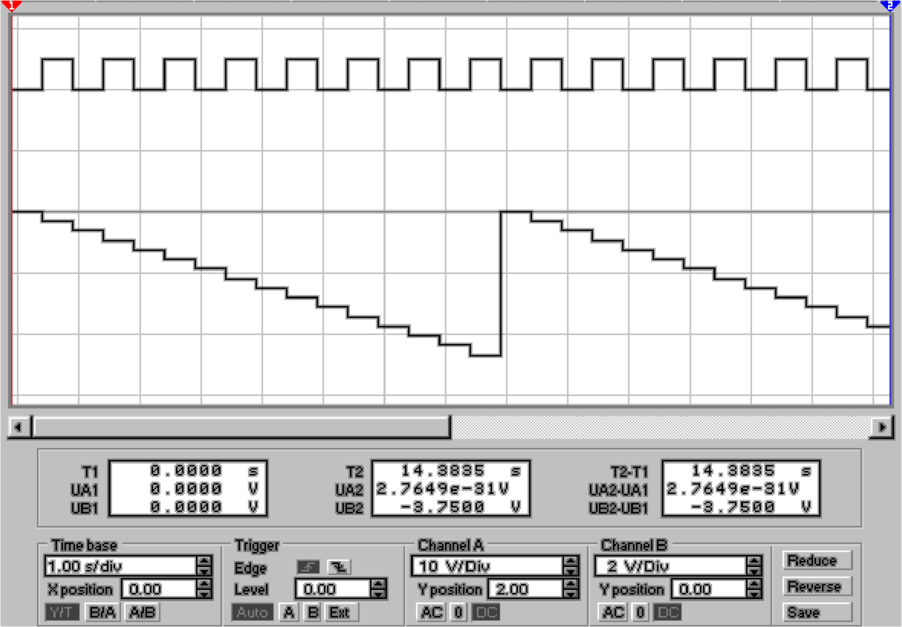
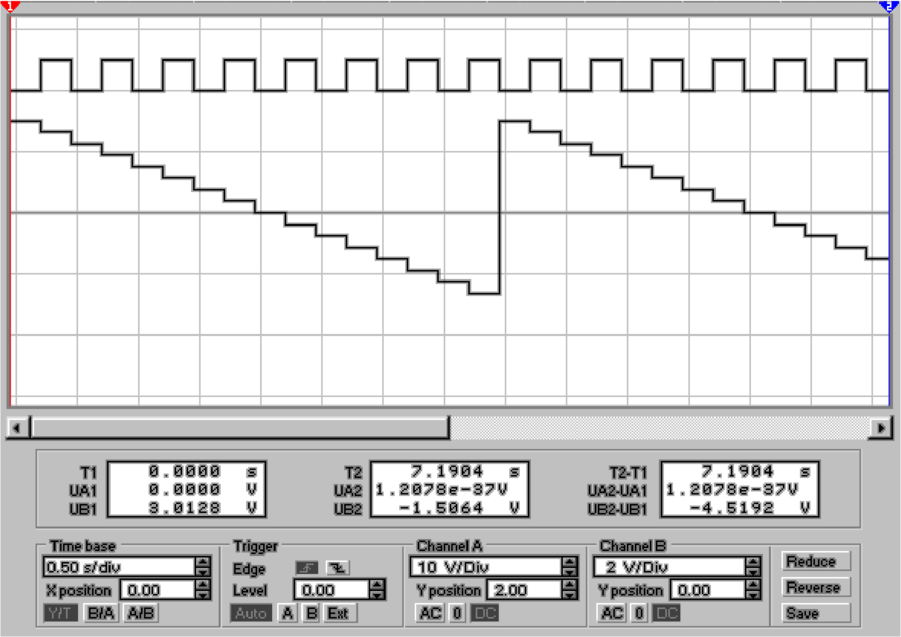
In der Abbildung 4.70 wird in der Mitte die Einrichtung des
Bitmustergenerators und unten das Ausgangssignal gezeigt.
Die Stufigkeit dieses Signals kommt dabei sehr schön zum
Ausdruck.
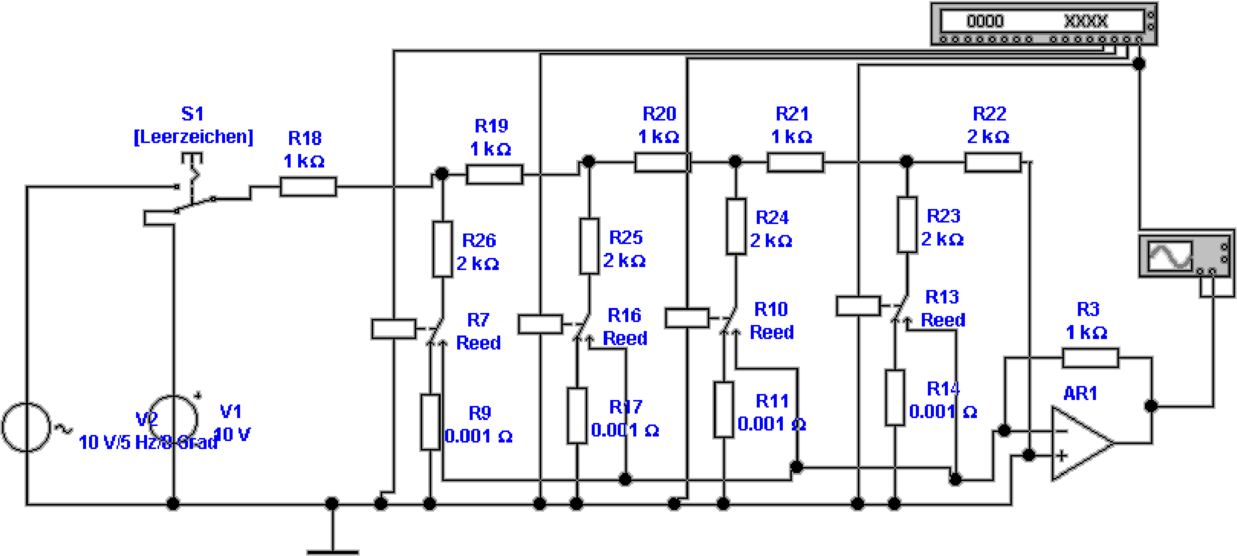
Digital/Analogwandler nach Abbildung 4.70 belastet die
Stromquelle sehr ungleichmässig. Deshalb wird in der Strom
durch die Widerstände nicht unterbrochen, sondern wie in
Abbildung 4.71 nur zwischen dem invertierenden Eingang
des Strom-Spannungswandlers und der Erde geschaltet.
Gleichzeitig erreicht man, dass über dem geschlossenen
Schalter keine Spannung abfällt, dass also Leckströme sehr
effektiv unterdrückt werden. Für die Dimensionierung der
Widerstände gilt Gleichung (4.83).
Der Digital-Analogwandler nach Abbildung 4.72 verwendet
ein R-2R-Netzwerk, bei dem nur zwei Widerstandswerte
vorkommen, nämlich R und 2R. Dieses Netzwerk kann wie
folgt verstanden werden. Wir betrachte das rechte Ende der
Kette, beginnend mit dem Knoten 1 zwischen R20, R21
und R24. der Knoten 2 liegt zwischen R21, R22 und R23.
Die Widerstände R23 und R24 speisen den Strom in den
Digital/Analog-Wandler. Dabei soll der Strom durch R24, I24
gleich dem doppelten des Stromes I23 durch R23 sein.
Damit gilt: U1 = 2U2. Somit können wir das folgende
Gleichungssystem aufstellen:
Eingesetzt ergibt sich
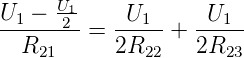 | (4.85) |
Diese Gleichung ist unabhängig von U1. Man bekommt
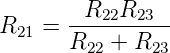 | (4.86) |
Wird in Gleichung (4.86) R23 = R22 gesetzt, so ist R21 = 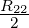 .
Am Knoten 1 hat die Kombination aus R21…R23 die Impedanz
R21 +
.
Am Knoten 1 hat die Kombination aus R21…R23 die Impedanz
R21 +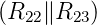 = R21 +
= R21 +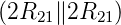 = R21 +R21 = 2R21 = R22.
Damit kann der Knoten 1 wie der Knoten 2 behandelt
werden: der Strom verdoppelt sich bei diesem Netzwerk, wenn
man nach links geht, und er halbiert sich, wenn man nach
rechts geht.
= R21 +R21 = 2R21 = R22.
Damit kann der Knoten 1 wie der Knoten 2 behandelt
werden: der Strom verdoppelt sich bei diesem Netzwerk, wenn
man nach links geht, und er halbiert sich, wenn man nach
rechts geht.
Das R-2R-Netzwerk hat den Vorteil, dass nur Widerstände,
die in der Grösse um den Faktor 2 variieren, auf der
Chipfläche hergestellt werden müssen. Damit ist diese
Struktur kompatibel zu der Halbleiterfertigung. Die grössten
Fehlern sind
- Widerstand der Schalter im eingeschalteten Zustand
- Offsetspannungen
- Bei grossen Bitzahlen werden die Ströme so klein,
dass thermische Ströme oder Rauschströme grösser
werden können.
Die Spannungsquelle wird mit dem Widerstand R21
belastet. R18 kann auch weggelassen werden. Dann ist die
Belastung der Referenzquelle R22.
Schliesslich ist es möglich, wie in Abb. 4.72 gezeigt, das
Netzwerk auch mit veränderlichen Spannungen zu betreiben.
Die Digitalzahl wirkt dabei wie ein Multiplikator.
Die Schaltung nach Abbildung 4.73 erweitert das
R-2R-Netzwerk mit einem bipolaren Ausgang.
Pulslängenmodulation
Bei den oben besprochenen Digital-Analog-Wandlern gibt
es zwei fundamentale Probleme:
- Beim Umschalten des MSB können
grosse Störsignale entstehen. je mehr Bit Auflösung
ein Wandler hat, desto schwieriger wird es, dieses
Problem in den Griff zu bekommen.
- Die Linearität kann bei sehr hochauflösenden
Wandlern nicht mehr garantiert werden.
- Und nicht zuletzt, die Kosten für einen Wandler
steigen überproportional mit seiner Bitzahl.
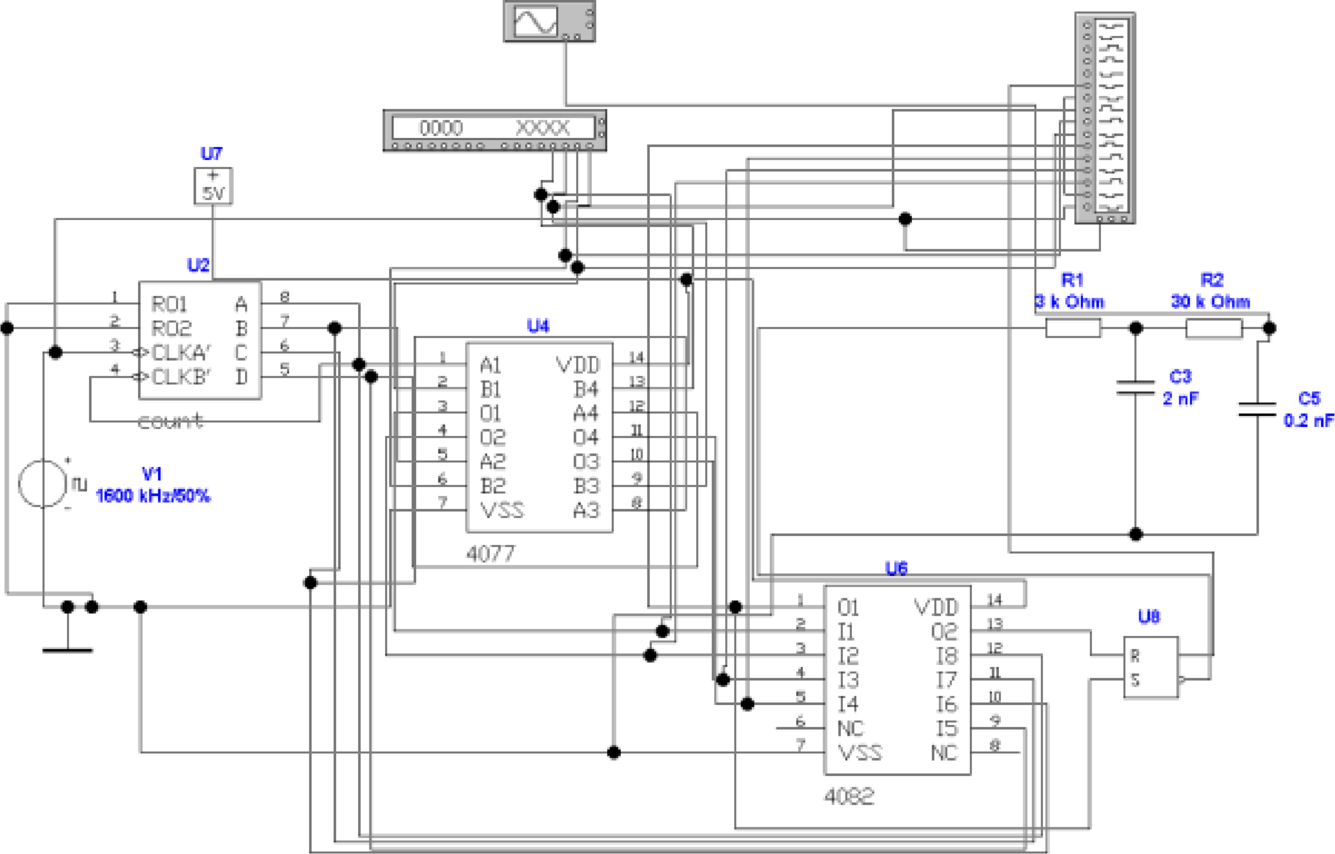
Dieses Problem kann umgangen werden, indem man
die Ausgangsspannung wie in Abb. 4.74 zwischen zwei
Spannungswerten hin- und herschaltet und dabei die
Pulslänge moduliert.
Das Eingangssignal stammt von dem Bitmustergenerator.
Um das Prinzip klarzumachen, verwenden wir nur zwei Bits.
Mit dem Taktgenerator V 1 wird der Binärzähler U2
angesteuert. Das XOR-Gatter U4 vergleicht jeweils ein Bit des
Zählers mit dem entsprechenden Bit des Bitmustergenerators.
Das AND-Gatter U13 detektiert, wenn beide Bit-Werte
vom Zähler und vom Bitmustergenerator gleich sind.
Dann wird das RS-Flip-Flop U8 zurückgesetzt. Mit der
fallenden Flanke von Bit B aus dem Zähler U1 wird
der Monoflop U6 getriggert. Sein Ausgangspuls setzt
das RS-Flip-Flop U8. Damit ist das Ausgangssignal von
U8 eins, solange der Zähler eine kleinere Zahl als der
Bitmuster-Generator hat. Das Eingangssignal könnte auch
von einem Computer kommen. Das Ausgangssignal wird Null
für den Rest der Periode. Damit ist diese Schaltung ein
digitaler Pulsweiten-Modulator. Schliesslich wird das
Ausgangssignal in der Schaltung A1 Tiefpassgefiltert (Die
Parameter ergeben ein Tschebyscheff-Tiefpassfilter dritter
Ordnung mit 0.5 dB Welligkeit und einer Grenzfrequenz von
10kHz).
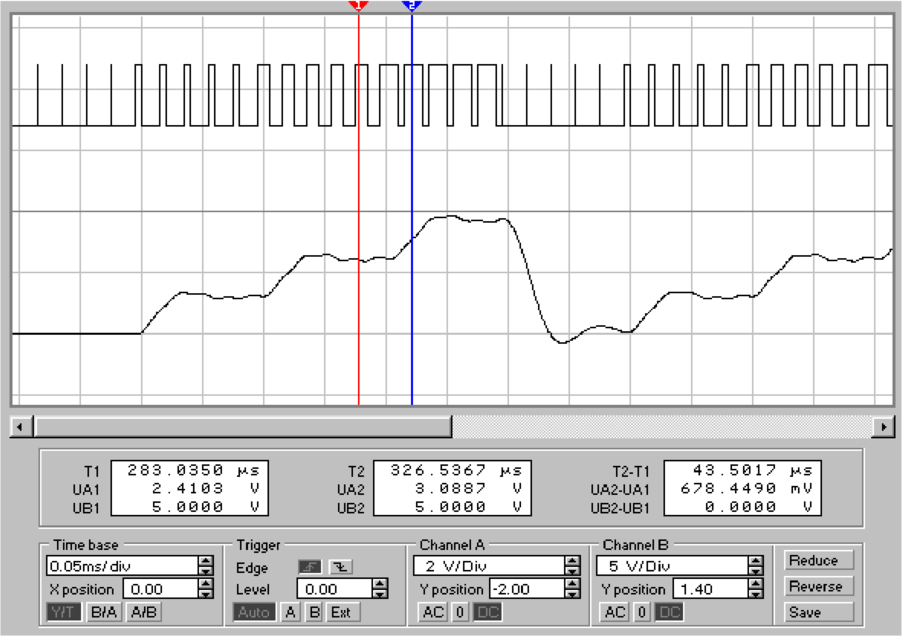
Die Abb. 4.74, unten zeigt in der oberen Hälfte des
Oszilloskpbildes das Pulsweitensignal und unten das gefilterte
Ausgangssignal. Die Bitstufen im 8 kHz-Takt sind klar
getrennt. Die Taktfrequenz ist dabei 200 kHz.
1-Bit Wandler
1-Bit-Wandler kombinieren das Pulslängen-Modulationsprinzip
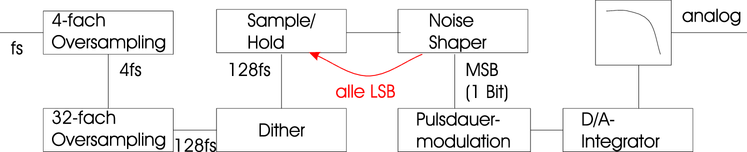
mit zusätzlicher digitaler Logik. Abbildung 4.75 zeigt eine
mögliche Schaltung aus einem CD-Spieler[HS93]. Das
abgetastete Signal wird zuerst 4-fach interpoliert (oversampled)
und dann 32-fach interpoliert. Aus der CD-Abtastfrequenz
von 44.1 kHz wurde nun eine Abtastfrequenz von 5.6 MHz.
Das Signal wird mit einem 352 kHz-Signal so digital
moduliert, dass die Ausgangsspannung um das wenigstwertige
Bit (LSB) schwankt. damit muss der Wandler konstant das
Ausgangssignal ändern: es können keine niederfrequenten
Störsignale entstehen. In einer digitalen Sample/Hold-Stufe
werden die Datenworte verdoppelt. Die Abtastfrequenz ist
nun 11.2 MHz. Aus diesem Signal wird das MSB-Bit im
Noise-Shaper abgetrennt und dem Pulsweiten-Modulator
(1-Bit!) zugeführt. Die nicht-verwendeten Signalbits werden
zum nächsten Datenbit im Sample/Hold dazu gezählt und
gehen so nicht verloren. Die Wandlung wird nun von einer
1-Bit Puls-Dichte-Modulatorstufe durchgeführt, deren
niedrigste Frequenz durch die 352kHz-Modulationsspannung
gegeben ist. Das Ausgangssignal wird nun durch einen
Integrator tiefpassgefiltert.
|
|
| Oversampling | Erhöhung der Bit-Zahl |
|
|
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 16 | 4 |
| 32 | 5 |
| 64 | 6 |
| 128 | 7 |
| 256 | 8 |
|
|
| |
| Tabelle 4.3.: | Erhöhung der Bitzahl durch oversampling |
Die Bitzahl m, die man gewinnen kann, hängt von der
Oversamplingrate r wie folgt ab:
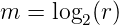 | (4.87) |
Tabelle 4.3 zeigt einige charakteristische Werte. Warum
funktioniert die 1-Bit-Wandlung, obwohl man im obigen
Beispiel ausrechnen kann, dass die Bitzahl 1 + 8 = 9 Bit ist.
das menschliche Ohr hat seine maximale Empfindlichkeit bei
1 kHz, so dass für diese Frequenz nochmals eine etwa 32-fache
Überabtastung resultiert. Damit ist die effektive Bitzahl
9 + 5 = 14. Der Noise-Shaper ermöglicht eine zusätzliche,
digitale Erhöhung der Quantisierung.
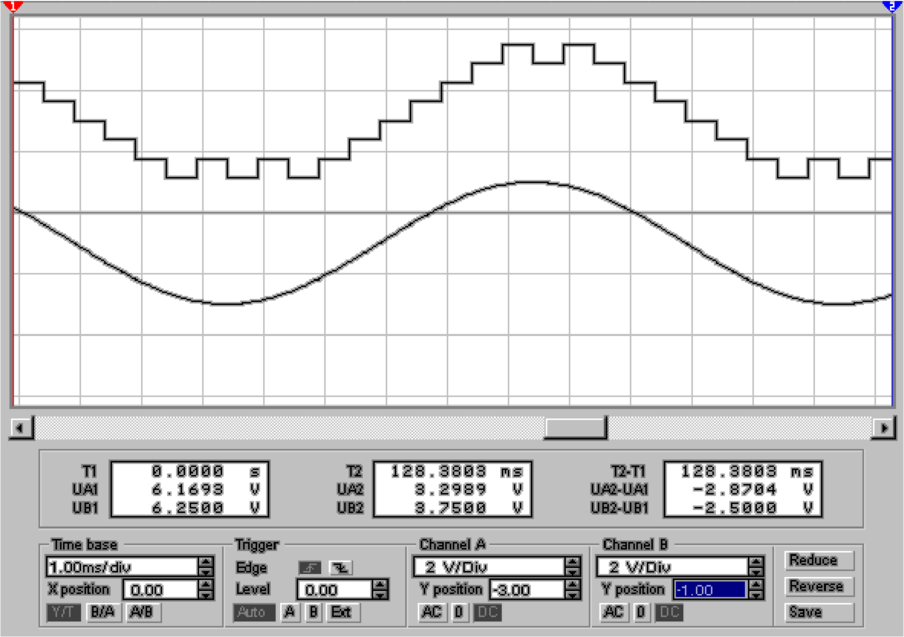
Oversampling
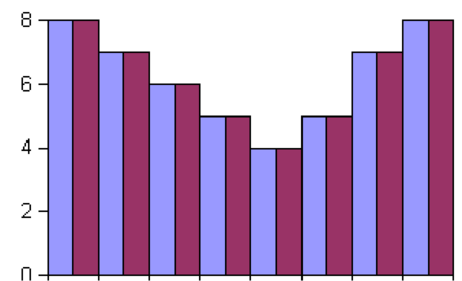
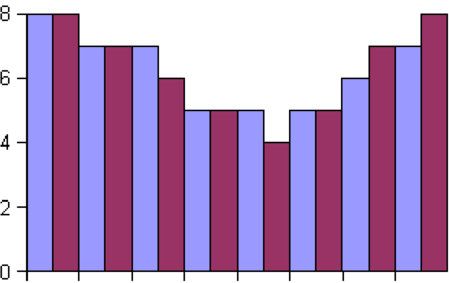
Die Funktionsweise des Oversampling wird in Abb.
4.76 gezeigt. Links wird das Ausgangssignal, wie es ein
3-Bit-Wandler erzeugen würde, gezeigt. Das mittlere
Bild stellt den Ausgang eines 2-Bit-Wandlers dar. Wenn
dabei das ursprüngliche Signal zwischen zwei möglichen
Ausgangswerten liegt, wird das Ausgangssignal zwischen den
beiden, dem ursprünglichen Signal benachbarten werten,
hin-und hergeschaltet. Der mittlere Teil von Abb. 4.76 zeigt
das entsprechende Signal. Der rechte Teil von Abb. 4.76 zeigt
das mit einem gleitenden Mittelwert gefilterte Ausgangssignal.
Betrachtet man nur die weinroten Balken im linken und im
rechten Diagramm, stellt man fest, dass sie identisch
sind.
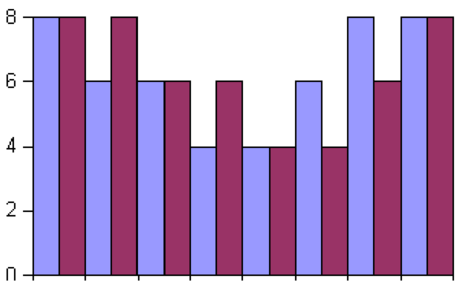
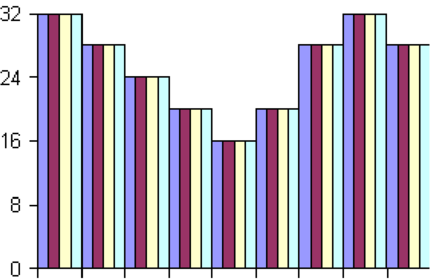
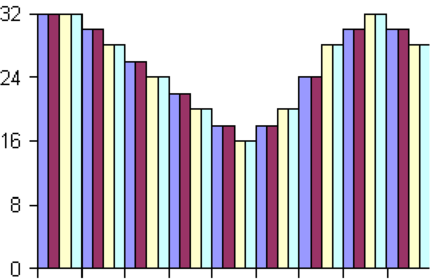
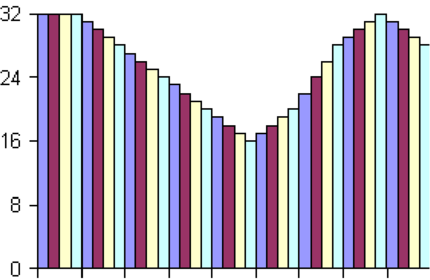
Abb. 4.77 zeigt ein vierfach-Oversampling. Links ist das
ursprüngliche Signal mit 4-Bit Auflösung. Das mittlere
Bild zeigt das Interpolationsresultat wen jeweils über
2 und 2 Ausgangsbalken gemittelt wird. Rechts ist
das voll interpolierte 4-fach Oversampled-Signal. bei
CD-Plattenspielern wird bei 16-Bit Digital-Analogwandlern
maximal 16-fach überabgetastet. mehr macht nicht Sinn, da
16-Bit Wandler damit an ihre Geschwindigkeitsgrenze
kommen[HS93]. Das verfahren ist bekannt unter dem Namen
High-Bit-Verfahren.
Wie das Beispiel mit der Pulsweiten-Modulation gezeigt
hat, kann es sinnvoll sein, die Taktfrequenz sehr hoch zu
setzen und die Auflösung durch Filteroperationen im
digitalen Bereich zu erhalten. Werden weniger Bits und
preiswerte analoge Filter verwendet, nennt man das Verfahren
Bitstream-Verfahren.
MASH-Verfahren
Eine Weiterentwicklung des Bitstream-Verfahrens ist
die MASH-Technik. MASH heisst Multi-Stage noise
SHaping. Dabei wird, wie in Abb. 4.78 gezeigt, der
Puls-Weiten-Modulator mit mehr als einem Bit angesteuert.
Die Pulsweite kann dabei in 2k Schritten eingestellt werden.
Damit hat man eine höhere Auflösung im Wandler. Da
die Bitzahl klein bleibt, ist die notwendige Präzision
gewährleistet. Die Netto-Auflösung ist dann
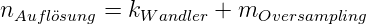 | (4.88) |
Bei einem Pulsweiten-Modulator mit 4-Bit Auflösung, der
mit 45,1 MHZ betrieben wird (1024 Oversampling) stehen bei
44.1 kHz 14 Bit zur Verfügung. Bei dem für den Hörer
wichtigen Frequenzbereich von unter 5 kHz stehen nun 17 Bit
zur Verfügung.
4.1.8.2. Analog/Digital-Wandler
Analog-Digital-Wandler bereiten analoge Eingangssignale in
digitale Signale auf. Da es bei der Analog-Digital-Wandlung
keine so einfachen Konzepte wie das Successive Approximation
Verfahren gibt, ist die Umsetzung von analogen in digitalen
Signale meistens mit einem grösseren Aufwand verbunden.
Direkte Verfahren
Das am einfachsten zu begreifende Verfahren
für die Analog-Digital-Wandlung ist das
Direktverfahren ,
wie es in Abb. 4.79 gezeigt wird. Als Beispiel wird eine 2-Bit
Wandlung gezeigt. Die Referenzspannung wird durch eine
Teilerkette R1…R5 in gleichabständige Spannungswerte
gewandelt. dabei sind die Spannungswerte jeweils um ein
halbes LSB verschoben, um eine korrekte Wandlung zu
erreichen. Die Komparatoren V R1…V R4 vergleichen die
Eingangsspannung mit den Referenzwerten. Die D-Flipflops
U5…U8 transferieren zu einem genau festgelegten Zeitpunkt
die Komparatorsignale an den Ausgang. Diese sind im
Logikanalysator (Abb. 4.79, unten links) zu sehen. der
Priority-Encoder U2 gibt nun ein 2-Bit-Ausgangssignal, das
von der Adresse des höchstwertigen Komparators bestimmt
ist. Die LED-anzeige stellt den Wert dar. Das Oszilloskopbild
in Abb. 4.79, unten rechts, zeigt das Verhältnis des obersten
Komparators zum Eingangssignal.
Analog-Digital-Wandler nach diesem Prinzip arbeiten
bis in den GHz-Frequenzbereich. Damit dienen sie zur
Wandlung von Videosignalen und werden in digitalen
Höchstfrequenz-Oszilloskopen eingesetzt. Sie werden
typischerweise mit 8-Bit Auflösung hergestellt.
Nachlaufverfahren
Das Nachlaufverfahren nach Abb. 4.80 verwendet einen
Digital-Analog-Wandler und eine Nachlaufregelung
um ein Analogsignal zu wandeln. Das Eingangssignal
wird im Subtrahierer A1 vom Ausgangssignal des
Digital-Analog-Wandlers U7 abgezogen. Der Komparator V R1
vergleicht die Differenz mit 0 und steuert so die Zählrichtung
des Up/Down-Zählers U11. Der Ausgang dieses Zählers
steuert den Digital-Analog-Wandler U7. Das Signal wird
auch in der 7-Segment-Anzeige und im Logikanalysator
angezeigt.
Die Abb. 4.80 unten links zeigt das Bild des Logikanalysators.
Unten rechts wird schliesslich das Ausgangssignal des
Digital-Analog-Wandlers mit dem Eingangssignal verglichen.
Nachlaufende Analog-Digital-Wandler benötigen
Digital-Analog-Wandler mit monotoner Ausgangskennlinie.
Sie sind sehr schnell bei kleinen Änderungen, benötigen aber
bis zu 2nT
takt zum wandeln eines Spannungssprunges um n
Bits.
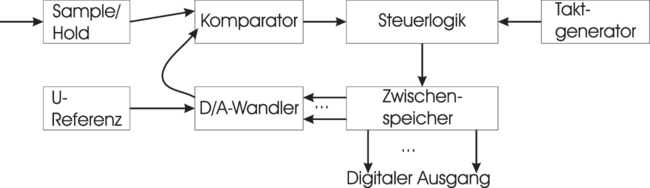
Wägeverfahren
Beim Wögeverfahren (auf englisch: Successive Approximation)
wird der gesuchte Zahlenwert schrittweise ermittelt. Abb. 4.81
zeigt das Blockschema eines Wandlers nach dem Wägeverfahren.
Die Eingangsspannung wird in einem Sample/Hold-Glied
zwischengespeichert .
Die Wandlung läuft nun folgendermassen ab:
- Die Steuerlogik setzt das höchstwertige Bit.
- Der Komparator vergleicht das Ausgangssignals des
Digital-Analog-Wandlers (jetzt die halbe
Referenzspannung Uref) mit dem Eingangssignal. Ist
das Eingangssignal grösser, bleibt das Bit gesetzt,
sonst wird es zurückgesetzt.
- Nun wird das nächste Bit gesetzt. Die Spannung
am Digital-Analog-Wandler ist nun Uref∕4 oder
3Uref∕4, je nach Ausgang des ersten Schrittes.
- Das zweite Bit wird nun
gelöscht, wenn die Eingangsspannung kleiner als die
Ausgangsspannung des Digital-Analog-Wandlers ist.
- Die obige Prozedur wird für jedes Bit wiederholt.
- Bei einem n-Bit-Wandler steht das Resultat nach n
Schritten zur Verfügung.
Wandler nach dem Wägeprinzip benötigen Digital-Analog-Wandler
die über den ganzen Spannungsbereich monoton sind. Die
Wandler haben einen mittleren Geschwindigkeitsbereich, bis
einige 10 MHz Taktrate. Dies heisst Wandelzeiten um die 1
μs.
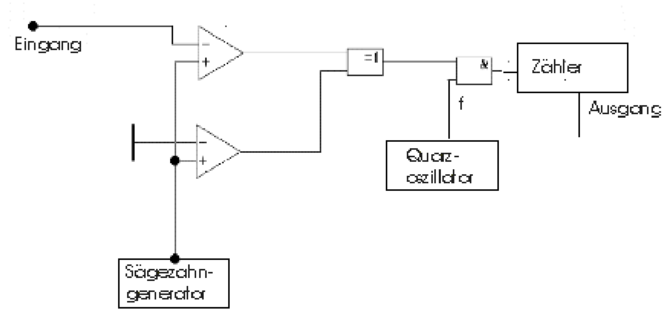
Integrierende Verfahren
Integrierende Analog-Digital-Wandler können sehr einfach
aufgebaut werden. Abbildung 4.82 zeigt einen Wandler nach
dem Sägezahnverfahren. Zwei Komparatoren vergleichen die
Sägezahnspannung mit Null und mit der Eingangsspannung.
Während die Sägezahnspannung zwischen Null und der
Eingangsspannung ist, wird der Quarzoszillator auf den
Zähler geschaltet. Die Sägezahnspannung hat den folgenden
Funktionsverlauf:
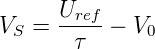 | (4.89) |
Die Zeit, während der der Zähler angesteuert wird,
ist:
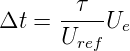 | (4.90) |
In der Zeit werden die Schwingungsperioden T des
Quarzoszillators gezählt. der Zählerstand ist am Ende der
Wandlung:
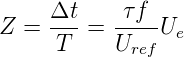 | (4.91) |
Das Sägezahnverfahren funktioniert theoretisch hervorragend.
In der Praxis gibt es damit aber fast unüberwindliche
Probleme.
- Die Frequenzunsicherheit (Jitter) des
Sägezahnoszillators begrenzt die Genauigkeit.
- Drift und der Einfluss der Temperatur verändern
die Schaltschwellen und beeinflussen damit die
Genauigkeit.
- Kondensatoren sind schwer mit genügender
Genauigkeit zu bekommen.
- Durch den Quarzoszillator und die weiteren
Komponenten ist die Schaltung relativ teuer.
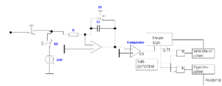
Die Abbildung 4.83 zeigt einen Wandler nach dem
Dual-Slope-Prinzip. Zuerst wird der Kondensator Ci mit dem
Schalter S3 entladen. Dann wird, gesteuert durch die
Steuerlogik, das Eingangssignal während einer festen Zeit t1
integriert. Dann wird das Eingangssignal vom Integrator
getrennt und und die Referenzspannung Uref integriert, bis
die Ausgangsspannung des Integrators wieder Null ist. Der
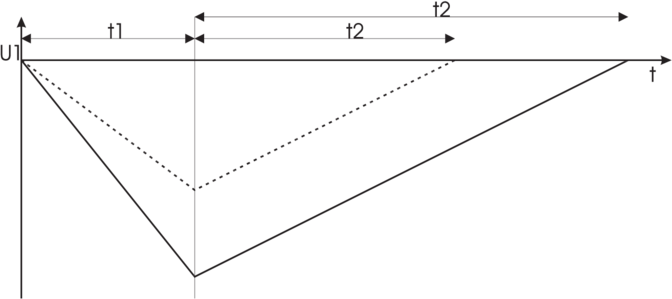
Spannungsverlauf ist in Abb. 4.84 für zwei verschiedene
Eingangsspannungen gezeigt.
Die beiden Zeiten werden vom Messdauerzähler und vom
Ereigniszähler bestimmt.
Der Ablauf nochmals in Kürze:
- Integration der Eingangsspannung über eine
vorgegebene Zeit t1
- Integration der fixen Referenzspannung (mit
umgekehrter Polarität wie die Eingangsspannung)
bis der Kondensator Entladen ist. Diese Zeit t2 wird
gemessen.
Die Ausgangsspannung am Integrator nach der Zeit t1
ist
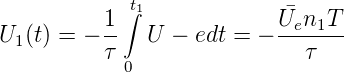 | (4.92) |
Dabei ist n1 die Anzahl Zählimpulse für die Zeit t1.
T ist die Periodendauer des Taktoszillators, τ ist die
Integrationskonstante des Integrators. Die Zeit t2 für das
Zurückintegrieren ist
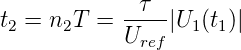 | (4.93) |
Daraus erhält man für den Zählerstand im Ergebniszähler:
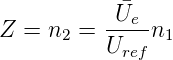 | (4.94) |
Die Eigenschaften des Dual-Slope-Verfahrens sind:
- Das Ergebnis hängt nicht von der Taktfrequenz ab,
da alle Zeiten von ihr abgeleitet werden.
- Der Absolutwert des R-C-Gliedes beeinflusst das
Ergebnis nicht. Durch die zweimalige Integration
sind die Integrationszeiten und Uref wichtig.
- Das Verfahren ist wenig Anfällig gegen
Störspannungen. Alle Frequenzen, die ein Vielfaches
von 1∕t1 sind werden unterdrückt.
- Die Referenzspannungsquelle muss die geforderte
Präzision haben.
- Der Integrationskondensator sollte
eine möglichst geringe Spannungshysterese haben,
also zum Beispiel Polystyrol als Dielektrikum haben.
- Dieser Wandler ist sehr billig herzustellen.
Sigma-Delta-Verfahren
Abbildung 4.85 zeigt einen Sigma-Delta-Wandler, der neuerdings
die bevorzugte Bauart für höchstauflösende Analog-Digital-Wandler
ist .
Der Wandler besteht aus einem Subtrahierer am Eingang, A1,
gefolgt von einem Integrierer, A2, und einem Hystereseschalter
bestehend aus A3 und S1. Die Eingangsspannung muss
zwischen den beiden Ausgangswerten des Schalters S1
liegen. Hier sind das 1V und -1V. Für Spannungswerte in
diesem Bereich funktioniert die Schaltung. Eine gute
Beschreibung dieses Funktionsprinzips gibt Jim Thompsons
Website [Tho95].
Für eine Eingangsspannung von 0V ergibt sich folgendes:
- Der Ausgang des Integrators A2 sei auf +1mV. Dann
ist S1 eingeschaltet und am Eingang B von A1 liegt
-1V. Die Ausgangsspannung von A1 ist dann -1V,
der Integrierer integriert mit einer Verstärkung von
10V/Vs gegen -1mV, der unteren Umschaltschwelle
von S1.
- Die Integrationsrate ist | − 1V |10V∕V s = 10V∕s.
Daraus ergibt sich die Integrationszeit zu tint =
2mV∕(10V∕s) = 0.2ms.
- Dann schaltet S1 auf +1V. Der Integrator A2
integriert nun von -1mv auf 1mV, wieder in 0.2 ms.
Das Ausgangssignal ist also ein 2.5kHz Rechteck mit
50% Tastverhältnis.
Wir nehmen nun an, dass Die Eingangsspannung 0.5 V sein
soll. Wir erhalten das folgende Resultat.
- Der Ausgang des Integrators A2 sei auf +1mV. Dann
ist S1 eingeschaltet und am Eingang B von A1
liegt -1V. Die Ausgangsspannung von A1 ist dann
0.5V − (1V ) = −0.5V , der Integrierer integriert
mit einer Verstärkung von 10V/Vs gegen -1mV, der
unteren Umschaltschwelle von S1.
- Die Integrationsrate ist | − 0.5V |10V∕V s = 5V∕s.
Daraus ergibt sich die Integrationszeit zu tint =
2mV∕(5V∕s) = 0.4ms.
- Dann schaltet S1 auf +1V. Der Ausgang von A1 ist
nun auf 0.5V − (−1V ) = 1.5V . Der Integrator A2
integriert nun von -1mv auf 1mV, nun mit einer Rate
von 15V∕s. Die Integrationszeit ist 0.133 ms. Das
Ausgangssignal ist also ein 1.875kHz Rechteck mit
75% Tastverhältnis. Das heisst, das Ausgangssignal
entspricht 1V ∗ 0.75 + (−1V ) ∗ 0.25 = 0.5V
Schliesslich soll die Eingangsspannung -0.5V sein.
- Der Ausgang des Integrators A2 sei auf +1mV. Dann
ist S1 eingeschaltet und am Eingang B von A1
liegt -1V. Die Ausgangsspannung von A1 ist dann
−0.5V − (1V ) = −1.5V , der Integrierer integriert
mit einer Verstärkung von 10V/Vs gegen -1mV, der
unteren Umschaltschwelle von S1.
- Die Integrationsrate ist |− 1.5V |10V∕V s = 15V∕s.
Daraus ergibt sich die Integrationszeit zu tint =
2mV∕(15V∕s) = 0.133ms.
- Dann schaltet S1 auf +1V. Der Ausgang von A1
ist nun auf −0.5V − (−1V ) = 0.5V . Der Integrator
A2 integriert nun von -1mv auf 1mV, nun mit einer
Rate von 5V∕s. Die Integrationszeit ist 0.4 ms. Das
Ausgangssignal ist also ein 1.875kHz Rechteck mit
25% Tastverhältnis. Das heisst, das Ausgangssignal
entspricht 1V ∗ 0.25 + (−1V ) ∗ 0.75 = −0.5V
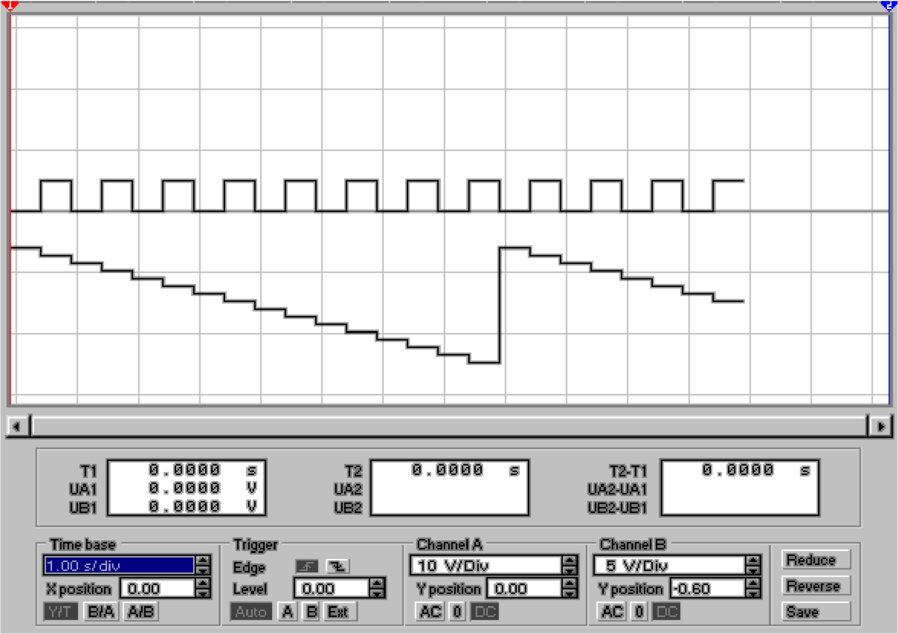
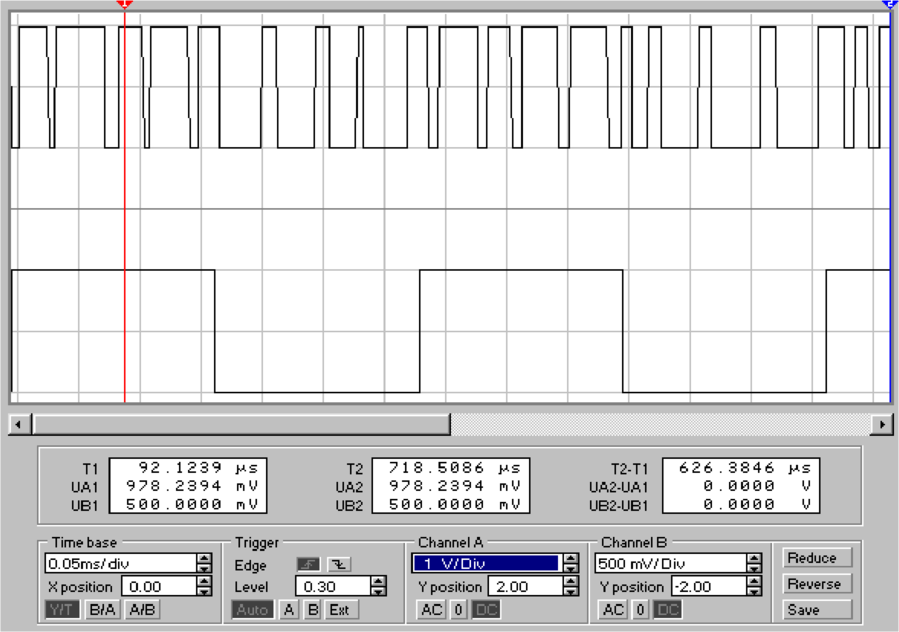
Die Schaltung nach Abb. 4.85 zeigt diese Eigenschaften.
Der untere Teil der Abbildung zeigt auf der oberen
Oszilloskopspur das Ausgangssignal von S1 und unten das
Eingangssignal. Die Schaltung erzeugt also ein Rechtecksignal,
bei dem das Tastverhältnis
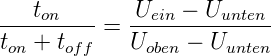 | (4.95) |
Die Wandlung geschieht nun, indem man mit einer
höheren Taktfrequenz zählt, wie oft Einsen und Nullen im
Rechtecksignal auftreten. Hier könnte man zum Beispiel mit
einem MHz zählen. Man würde folgendes erhalten
|
|
|
| Spannung | Anzahl 1 | Anzahl 0 |
|
|
|
| 0V | 500 | 500 |
| -0.5V | 250 | 750 |
| 0.5V | 750 | 250 |
|
|
|
| |
Die Schaltung hat also, ohne grossen Aufwand 10 Bit
Präzision. Sie hat folgende Eigenschaften:
- es gibt kein Aliasing bei der Umwandlung in den
Bitstrom. Da bei der Digitalisierung nicht abgetastet
wird, gibt es kein Aliasing.
- Prinzipbedingt gibt es keine fehlenden Codes.
- Das Wandlerverhalten ist absolut monoton und
linear.
- Der Wandler ist unempfindlich gegen steile
Flanken, gegen Rauschen und gegen hochfrequente
Störungen.
- Aliasing kann auftreten, wenn die digitale
Abtastfrequenz ungeschickt (zu tief) gewählt ist.
Die Funktion des Integrators ist, eine Tiefpassfilterung zur
Verfügung zu stellen. Wir haben die Schaltung mit einem Baustein
aufgebaut, sie wird als Sigma-Delta-Wandler (ΣΔ-Wandler)
erster Ordnung bezeichnet. Mit einer höheren Ordnung kann das
Tastverhältnis
schneller an das Eingangssignal angepasst werden[Kho98].
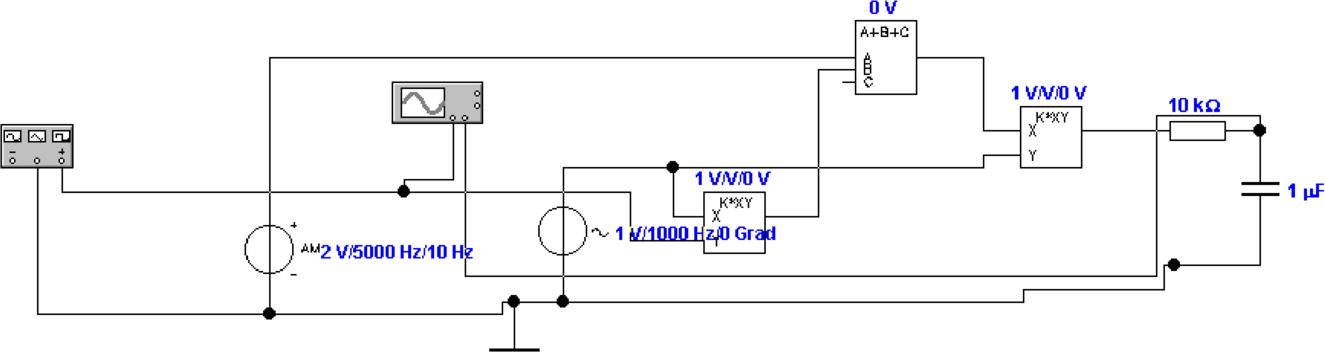
4.1.9 Lock-In Verstärker am Beispiel des AD630 Chips
Zur Messung von periodischen Signalen verwendet man häufig
Lock-In Verstärker. Der Kern jedes Lock-In-Verstärkers ist ein
synchroner Gleichrichter. der synchrone Gleichrichter in Abb.
4.86 ist ein Multiplizierer. Es können aber auch einfache
Umschalter für die Polarität verwendet werden.
Die Ausgangsspannung wird durch das folgende Integral
berechnet:
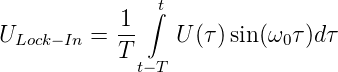 | (4.96) |
Hier ist sin(ω0τ) die Referenzspannung und Ue(t) die
Eingangsspannung. Die Integration wird normalerweise, wie
auch in der Abbildung 4.86, mit Tiefpassfiltern durchgeführt.
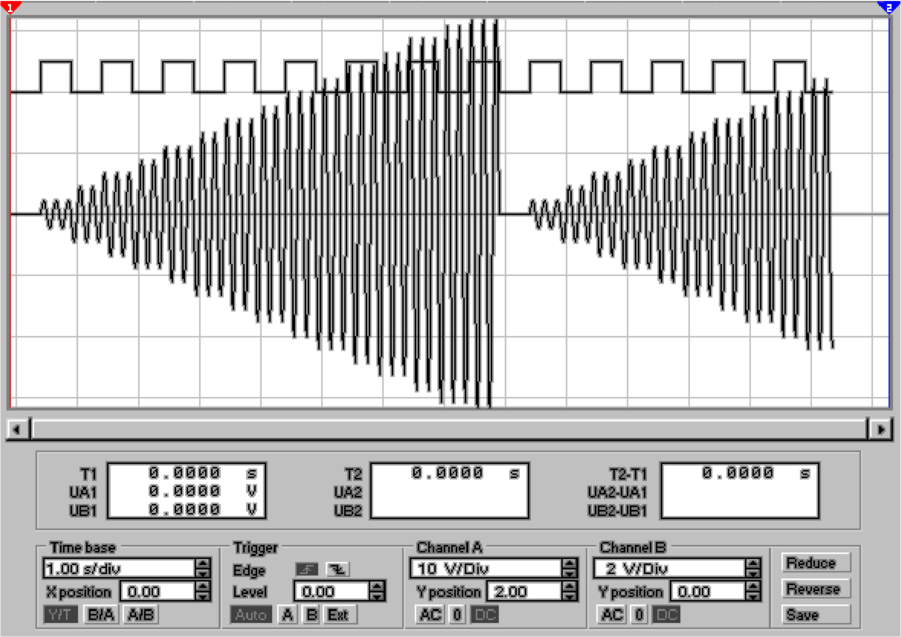
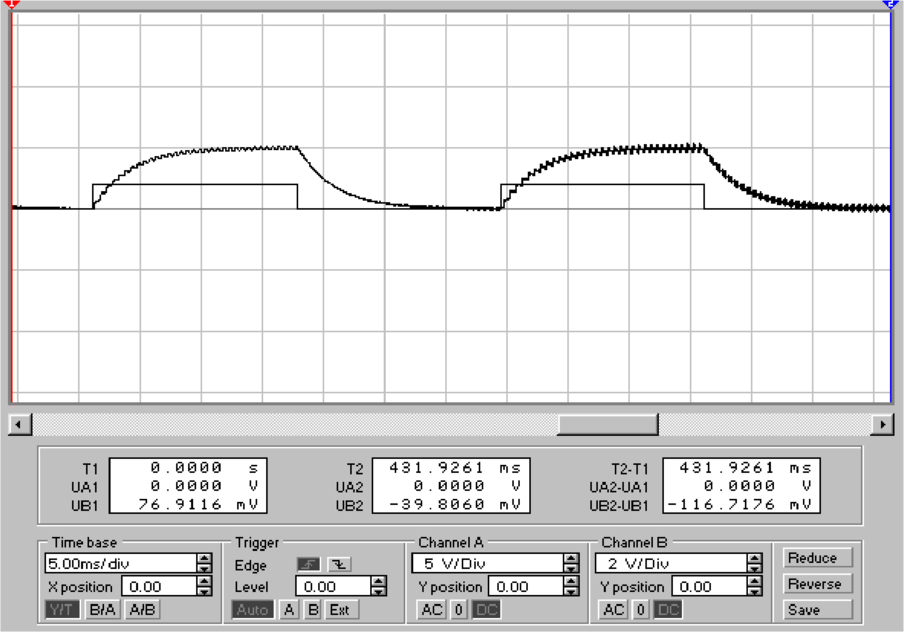
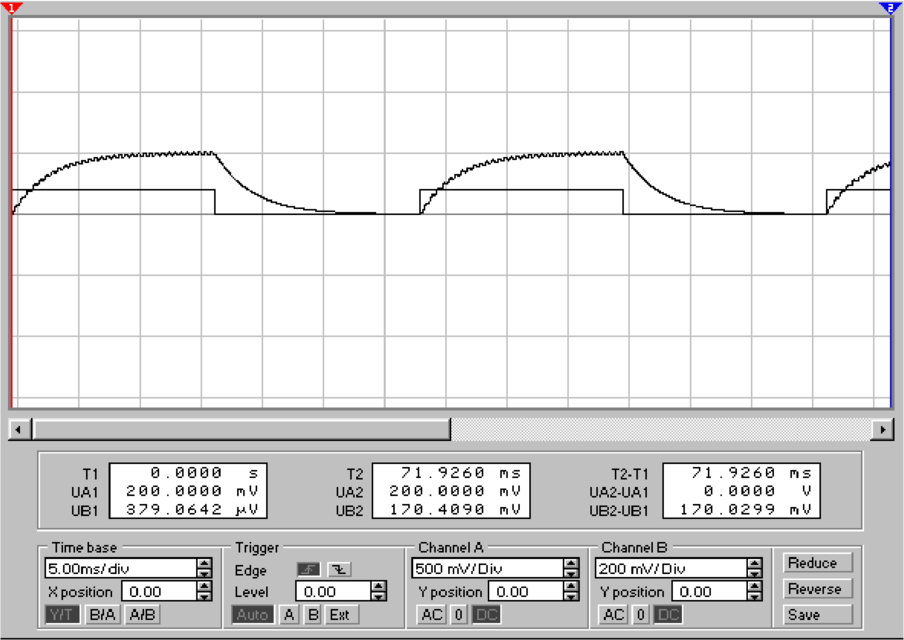
Die untere Hälfte von Abbildung 4.86 zeigt das Ausgangssignal
des Lock-In-Verstärkers. Dabei wird eine Signalspannung von
2V bei 1 kHz und eine Störspannung von 2 V bei 5 kHz
als Eingangssignal verwendet. Die Integrationszeit ist
τ = 3kΩ ×1μF = 3ms. Die Nutz-Eingangsspannung wird alle
15 ms von ihrer Spannung von 2V auf 0V geschaltet. 15 ms
später wird sie wieder eingeschaltet.
Meistens wird in Lock-In-Verstärkern das Eingangssignal
nicht mit dem Referenzsignal multipliziert, sondern nur die
Verstärkung zwischen den Werten +1 und -1 umgeschaltet.
Die Funktion des Lock-In-Verstärkers mit periodischer
Umschaltung kann man mathematisch wie folgt formulieren:
Die Schaltspannung S(t) wird in eine Fourierreihe
entwickelt:
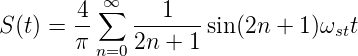 | (4.97) |
Wir nehmen im weiteren an, dass die Eingangsspannung
Ua(t) sinusförmig und ein ganzzahliges Vielfaches der
Referenzfrequenz ωe = mωst ist.
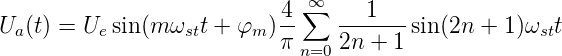 | (4.98) |
Für sinusförmige Schwingungen gelten die folgenden
Beziehungen:
Damit wird die gemittelte Ausgangsspannung des
Lock-In-Verstärkers
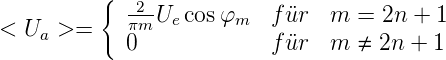 | (4.101) |
Bei einem Analogmultiplizierer erhält man
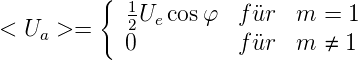 | (4.102) |
Anders als bei dem Detektor mit Umschalter ist die
Ausgangsspannung nur dann ungleich Null, wenn die
Frequenzen von Eingangsspannung und Referenzspannung
gleich sind. Bei Umschaltern ist der Lock-In-Verstärker auch
auf die Harmonischen des Eingangssignals empfindlich.
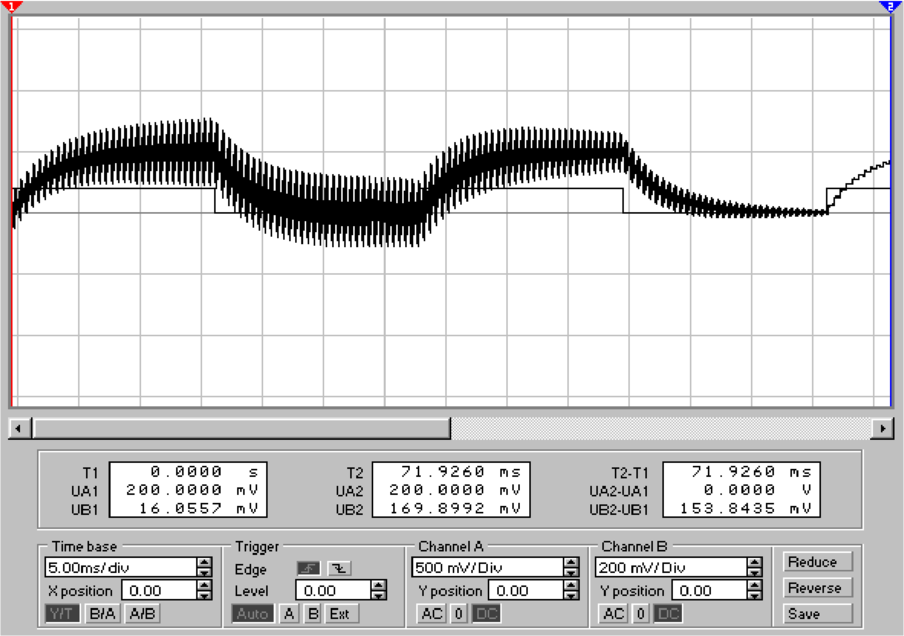
Die Abb. 4.87 zeigt den Einfluss von Störspannungen
und der Filterzeitkonstanten. Die linke Seite zeigt das
Ausgangssignal, wenn das Eingangssignal auf 0.2 V gesetzt
wird und wenn das Störsignal quasi ausgeschaltet ist. Das 10
mal stärkere Störsignal ist in der Mitte wieder eingeschaltet.
Durch Verlängerung der Integrationszeit in der rechten
Seite kann das Signal-zu Störsignal-Verhältnis verbessert
werden.
Die Bandbreite des Detektors hängt von der Integrationszeit τ
ab. Es gilt
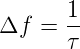 | (4.103) |
Man kann durch Integration über mehrere Sekunden in
einem Lock-In-Verstärker leicht Frequenzen von einigen kHz
mit Bandbreiten im mHz-Bereich messen.
Multipliziert man das Eingangssignal mit sin ωstt und auch
cos ωstt, so kann man sowohl die Amplitude wie auch die
Phase über die Beziehungen im rechtwinkligen Dreieck
bestimmen.
Ein Lock-In-Verstärker auf einem Chip ist der AD630.
Der Chip beinhaltet Widerstände, so dass der eine
Eingangsverstärker als invertierender und der andere als
nicht-invertierender Verstärker aufgebaut ist. Der AD630
arbeitet als Lock-In-Verstärker, mit der Referenzfrequenz am
Eingang des Komparators die abwechseld die beiden Eingänge
auf den Ausgang schaltend.
Der Lock-In-Verstärker kann ein Signal, das etwa 10000
schwächer als das Störsignal (weisses Rauschen) ist,
detektieren.
Viele Lock-In-Verstärker werden heute mit DSPs aufgebaut
(siehe auch den Abschnitt 2.9).
[Nächste Seite] [Vorherige Seite] [vorheriges Seitenende]
[Seitenanfang] [Ebene nach oben]
©2002-2017 Ulm
University, Othmar Marti,  Lizenzinformationen
Lizenzinformationen

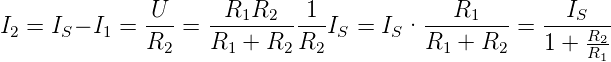
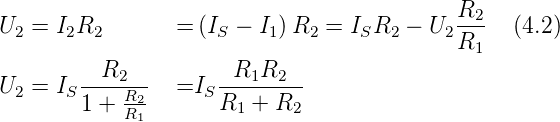
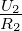 auf den Strom geschlossen.
auf den Strom geschlossen.

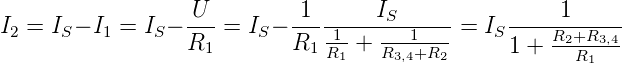
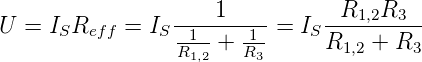
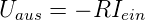
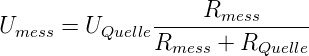
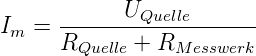
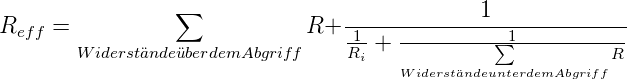
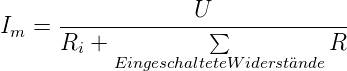
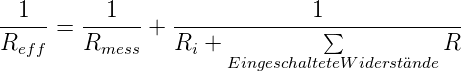
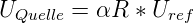
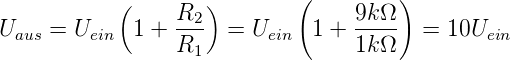
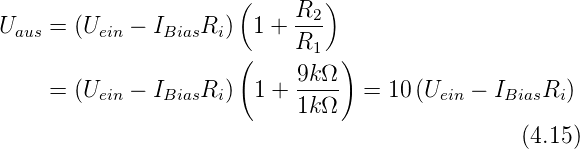
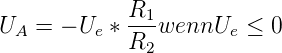
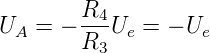
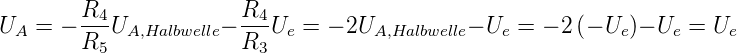
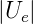
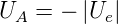
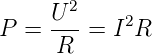
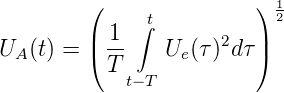
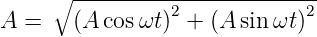
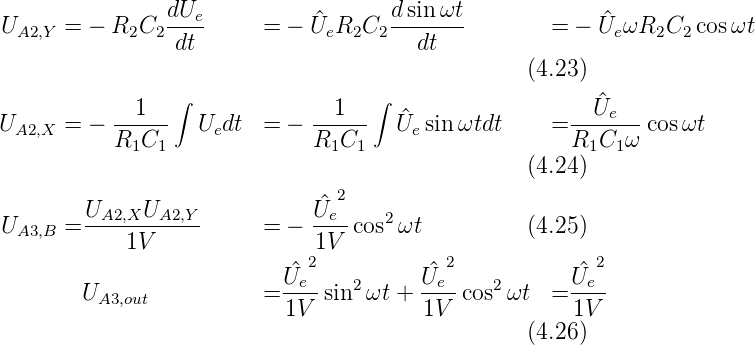
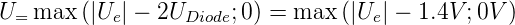
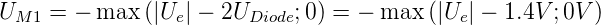
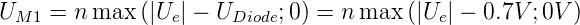
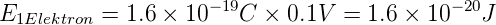
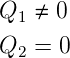
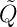
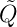
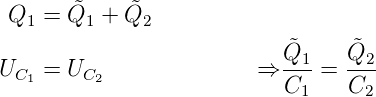
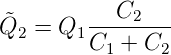
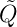
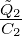
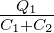 macht. Ebenso ist
ersichtlich, dass Die Spannung sehr schnell wieder abnimmt,
da Leckströme sogar im Modell eines idealen Verstärkers nicht
zu vermeiden sind.
macht. Ebenso ist
ersichtlich, dass Die Spannung sehr schnell wieder abnimmt,
da Leckströme sogar im Modell eines idealen Verstärkers nicht
zu vermeiden sind.
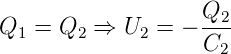
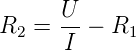
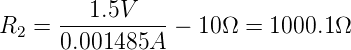
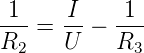
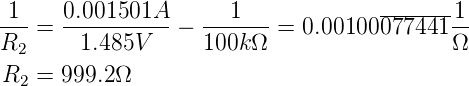
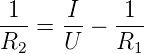
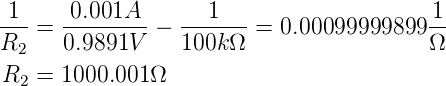
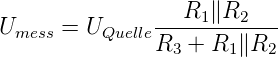
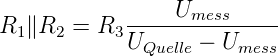
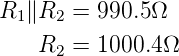
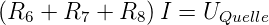
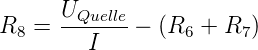
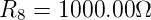
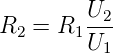
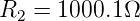
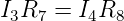
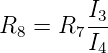
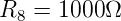
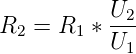
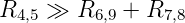
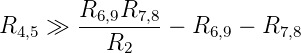
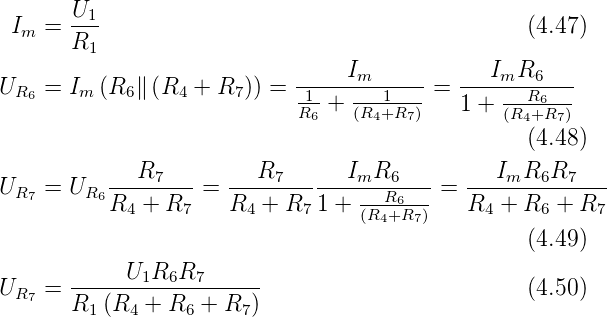
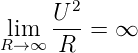
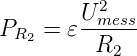
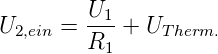
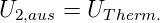
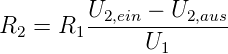
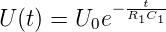
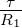
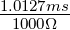
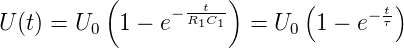
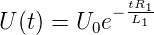
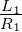 die Spannung gerade
die Spannung gerade
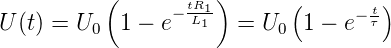
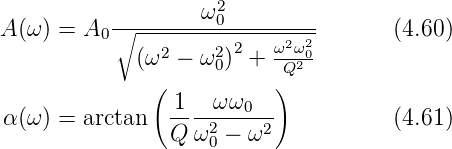
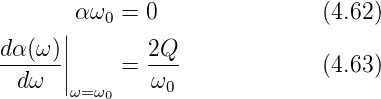
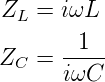

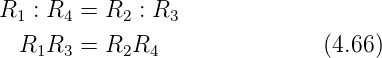
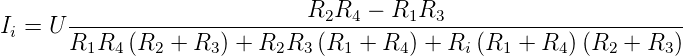
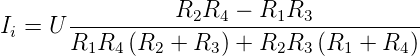
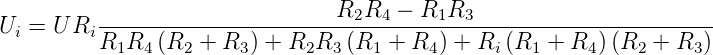
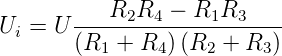
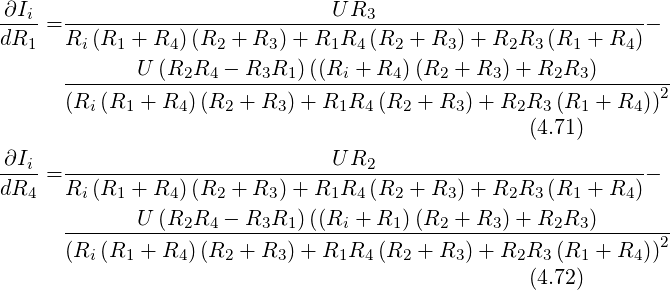
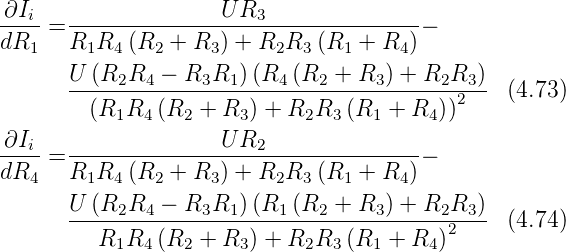
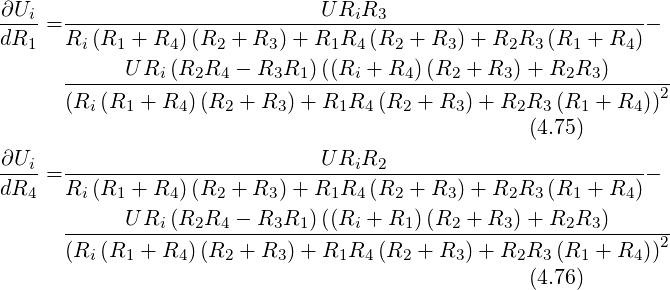
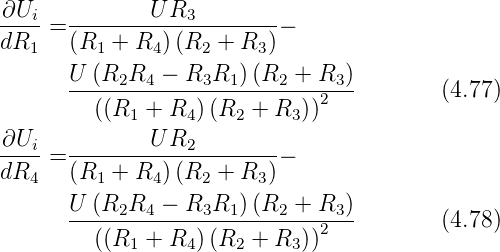
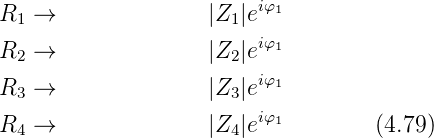
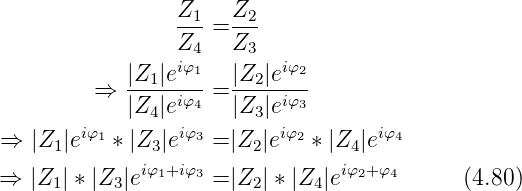
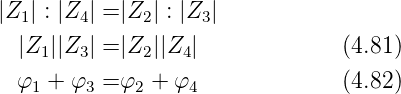
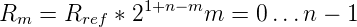
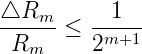

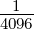
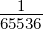
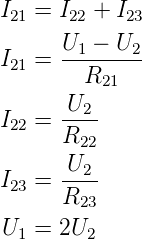
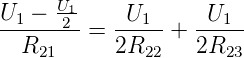
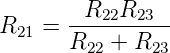
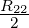 .
Am Knoten
.
Am Knoten 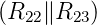
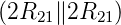

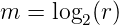
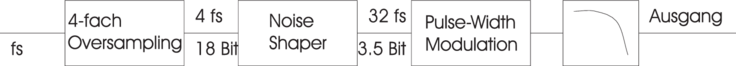
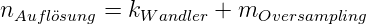
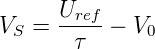
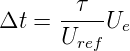
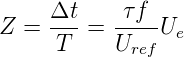
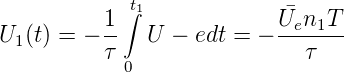
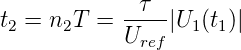
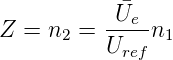
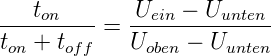
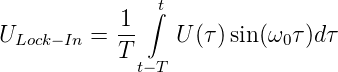
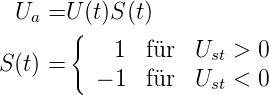
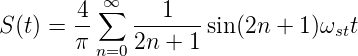
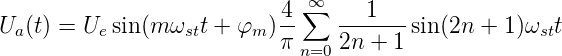
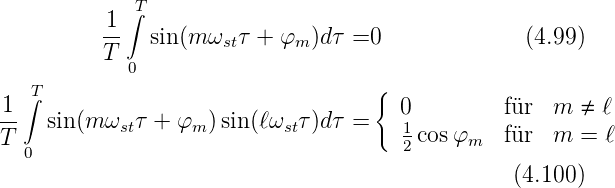
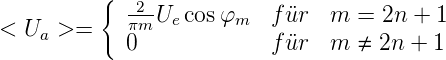
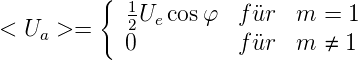
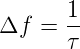
 Lizenzinformationen
Lizenzinformationen