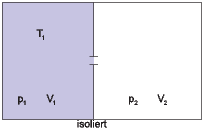
Überströmversuch


Überströmversuch
Beim Überströmversuch nach Abbildung 2.22 mit einem
idealen Gas bleibt die Temperatur erhalten, da U = U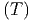 ist.
Erst wenn wir den Versuch mit einem realen Gas durchführen,
erhalten wir eine Temperaturänderung.
ist.
Erst wenn wir den Versuch mit einem realen Gas durchführen,
erhalten wir eine Temperaturänderung.
Auch beim realen Gas bleibt die Gesamtenergie (ein abgeschlossenes System) erhalten.
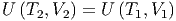 | (2.1) |
Bei einem realen Gas ziehen sich die Moleküle jedoch an. Beim Expandieren entfernen sie sich voneinander. Dadurch wird Energie benötigt, um sie der bei kleinen Distanzen negativeren potentiellen Energie zu höheren Werten zu bewegen. Diese Energie muss von der kinetischen Energie geliefert werden. Die Moleküle bewegen sich langsamer. Damit ist das Gas abgekühlt worden. Die Grösse der Abkühlung ist ein Mass für die Grösse der Anziehungskräfte.
Aus der van-der-Waals-Gleichung (2.13) folgt mit
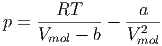 |
dass
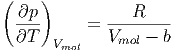 | (2.2) |
Andererseits betrachten wir den ersten Hauptsatz dU = TdS - pdV . Wir teilen durch dV und erhalten
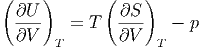 |
Mit der Maxwellrelation
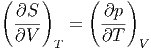 |
bekommen wir
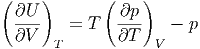 | (2.3) |
Wir setzen û = 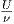 als innere Energie pro Mol und schreiben
die Gleichung für molare Grössen um.
als innere Energie pro Mol und schreiben
die Gleichung für molare Grössen um.
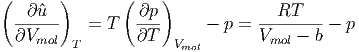 | (2.4) |
Wir setzen Gleichung (2.2) ein und erhalten
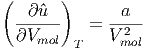 | (2.5) |
Bei einem idealen Gas wäre a = 0. Damit wäre û unabhängig V mol.
Mit der Gleichung (2.18) bekommen wir
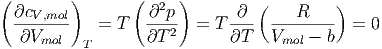 | (2.6) |
Die molare Wärmekapazität bei konstantem Volumen hängt also nicht vom Volumen ab, sondern nur von der Temperatur
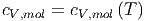 | (2.7) |
Damit kann dass Differential der molaren inneren Energie wie folgt geschrieben werden:
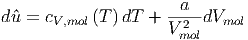 | (2.8) |
Die Differenz der molaren inneren Energie bekommen wir dann durch Integration
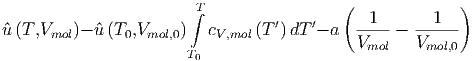 | (2.9) |
wobei die Integration des zweiten Summanden ausgeführt wurde. Alternativ kann das Resultat auch so geschrieben werden
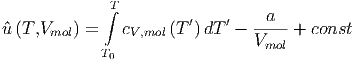 | (2.10) |
Beim Ausströmprozess kann sich die molare innere Energie nicht ändern, da wir ein abgeschlossenes System betrachten.
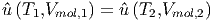 |
Dies ist äquivalent zu
∫
T0T2
cV ,mol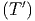 dT′-∫
T0T1
cV ,mol dT′-∫
T0T1
cV ,mol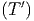 dT′ dT′ | = ∫
T1T2
cV ,mol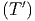 dT′ dT′ | ||
= a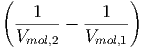 | (2.11) |
Betrachten wir einen Prozess mit einer kleinen Temperaturänderung T2 - T1 « T2, so ist die molare Wärmekapazität bei konstantem Volumen konstant.
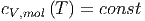 |
Dann sind die Integrale in Gleichung (2.11) lösbar
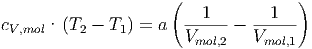 | (2.12) |
Lösen wir nach der Temperaturdifferenz auf, erhalten wir
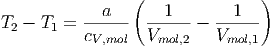 | (2.13) |
Beim Ausströmversuch ist V mol,2 > V mol,1. Deshalb gilt für alle van-der-Waals-artigen Gase T2 < T1.
| Der Überströmversuch sagt aus, wie gut ein
Gas das ideale Gas approximiert. Aus der
Temperaturerniedrigung kann der Binnendruck
a gemessen werden. |
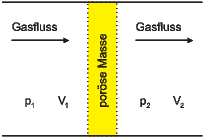
Modifizierter Überströmversuch
Beim Überströmversuch wie im vorherigen Abschnitt beschrieben ist das Gas nicht im Gleichgewicht. Deshalb modifizieren wir den Überströmkanal wie in Abbildung 2.22.1 gezeigt. Eine poröse Masse, ein Wattestopfen beispielsweise, ermöglicht, dass das Gas während dem gesamten Expansionsprozess im Gleichgewicht ist. Das Gas leistet Arbeit an dem Stopfen.
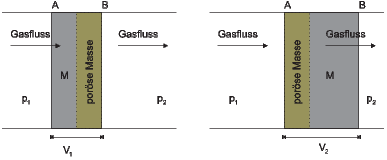
Bewegung der Masse M durch die poröse Membran
Abbildung 2.22.1 wird verwendet, um die Thermodynamik des Ausströmens im Gleichgewicht zu berechnen. Die Änderung der Energie ist
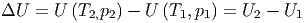 | (2.14) |
Die folgenden Energieaustausche passieren:
Die mechanische Arbeit ist
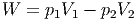 |
Wärme wird keine ausgetauscht, da wir isolierte Gefässe annehmen
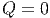 |
Die gesamte Änderung der inneren Energie ist dann
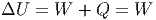 |
Damit wird Gleichung (2.14)
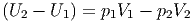 | (2.15) |
nachdem die Grössen vorher und nachher sortiert wurden, sieht man, dass gilt
 | (2.16) |
| Beim Überströmversuch mit einem porösen
Stopfen bleibt die Enthalpie H erhalten. |
Als Gleichung geschrieben, bedeutet dies
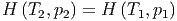 | (2.17) |
Für ein ideales Gas können wir mit der Zustandsgleichung schreiben
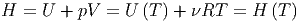 | (2.18) |
Da die innere Energie U eine mit der Temperatur monoton zunehmende Funktion ist, folgt aus der Konstanz der Enthalpie H1 = H2 sofort
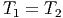 |
Das allgemeine Differential der Enthalpie ist
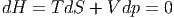 | (2.19) |
Wenn wir die Gleichung für das totale Differential der Enthalpie mit p und T als unabhängigen variablen aufschreiben erhalten wir
| 0 | = dH = T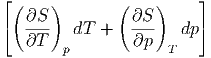 + V dp + V dp | ||
| 0 | = CpdT + ![[ ( ) ]
T ∂S- + V
∂p
T](td-20151116x.png) dp dp | (2.20) |
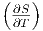 p und das
totale Differential von dS mit T und p als unabhängigen
Variablen eingesetzt.
p und das
totale Differential von dS mit T und p als unabhängigen
Variablen eingesetzt.
Beim Joule-Thomson-Effekt ist die Enthalpie konstant. Die Änderung der Temperatur mit dem Druck ist dann gegeben durch
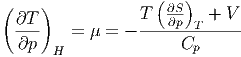 | (2.21) |
μ ist der Joule-Thomson-Koeffizient. Seine Einheit ist
![K m2K
[μ] = --- = -----
P a N](td-20151119x.png) |
Mit der Definition des Volumenausdehnungskoeffizienten und einer Maxwellrelation erhalten wir
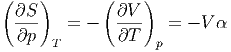 | (2.22) |
Wir setzen ein und verwenden die spezifische Wärmekapazität cp
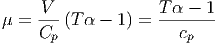 | (2.23) |
Für ideale Gase gilt α = 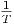 .
.
| Für ideale Gase ist der Joule-Thomson-Koeffizient
|
|
Bei realen Gasen kann μ sowohl positiv wie negativ sein.
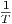
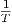
Die Kurve α(T,p) = 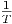 heisst Inversionskurve.
heisst Inversionskurve.
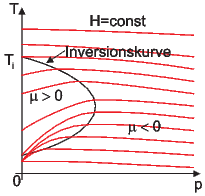
Kurven konstanter Enthalpie H (skizziert nach den Werten von N2. Die Inversionskurve ist schwarz eingezeichnet
Die maximale Temperatur, bei der μ = 0 ist, heisst Inversionstemperatur Ti.
| Gas | Ti |
| He | 34K |
| H 2 | 202K |
| N 2 | 625K |
Die molare Enthalpie ĥ von van-der-Waals-Gasen ist
| ĥ | = û + pV mol | ||
= 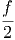 RT + RT + 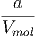 + V mol· + V mol·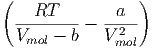 | |||
= RT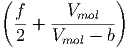 - -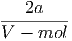 | (2.24) |
Da die Enthalpie konstant ist, berechnen wir
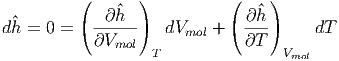 | (2.25) |
Die beiden partiellen Ableitungen können mit Gleichung (2.24) berechnet werden.
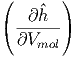 T T | = -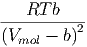 + + 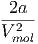 | (2.26) |
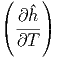 V
mol V
mol | = R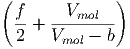 | (2.27) |
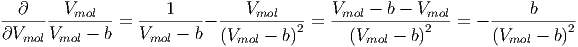 |
verwendet. Aus Gleichung (2.25) erhalten wir
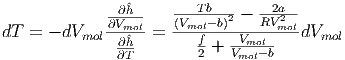 | (2.28) |
Wir erhalten in Gleichung (2.28) einen Vorzeichenwechsel, wenn
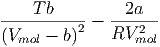 |
Wenn nun V mol » b ist, wenn also das Molvolumen viel grösser ist als das auf das Mol bezogene Eigenvolumen, können wir vereinfachen.
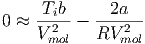 |
Damit wird die Inversionstemperatur
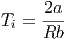 | (2.29) |
Wir hatten für das van-der-Waals-Gas die kritische
Temperatur Tk = 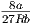 ausgerechnet. Sie hing, wie die
Inversionstemperatur Ti nur von a und b ab. Also sind Ti und
Tk voneinander abhängig.
ausgerechnet. Sie hing, wie die
Inversionstemperatur Ti nur von a und b ab. Also sind Ti und
Tk voneinander abhängig.
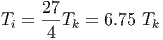 | (2.30) |
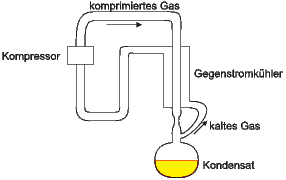
Luftverflüssigung nach dem Linde-Verfahren
Gase werden in der Regel mit dem Linde-Verfahren verflüssigt (siehe Abbildung 2.22.2). Beim Linde-Verfahren wird Gas durch einen Kompressor durch eine poröse Ausströmdüse gedrückt. ist die Anfangstemperatur unter der Inversionstemperatur Ti, wird das Gas bei der Expansion abgekühlt. Um den Prozess effizienter zu machen, wird das einströmende Gas durch einen Gegenstromkühler vorgekühlt. Ist das Gas genügend vorgekühlt, wird bei der Expansion die Temperatur so stark abgesenkt, dass das Gas verflüssigt wird. Stickstoff (N2) hat eine Inversionstemperatur von 625K und kann also mit dem Linde-verfahren direkt ohne weitere Hilfsmittel verflüssigt werden. Wasserstoff (H2 hat eine Inversionstemperatur, die unterhalb der Raumtemperatur liegt. Wasserstoff muss zum Beispiel mit flüssiger Luft vorgekühlt werden.
Helium mit einer Inversionstemperatur von 34K müsste mit H2 vorgekühlt werden, damit es im Linde-Verfahren durch den Joule-Thomson-Effekt verflüssigt werden kann. Dieses Verfahren wird nicht verwendet, da es zwar physikalisch möglich, aber viel zu gefährlich ist. Wie verflüssigt man also He? man entzieht dem He innere Energie, indem man es in einer Turbine Arbeit leisten lässt!
Wir haben bis jetzt die Zustandsgleichung des idealen Gases
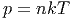 |
gesehen (n ist die Teilchendichte) sowie die Zustandsgleichung des van-der-Waals-Gases
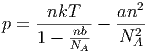 | (2.31) |
Beide Zustandsgleichungen, sowohl die des idealen Gases wie auch die des van-der-Waals-Gases, sind Näherungen. Wir können die Zustandsgleichung eines realen Gases beliebig genau annähern, indem wir p als Taylorreihe schreiben.
![p = kT [n + B (T )n2 + B (T )n3 + ...]
2 3](td-20151149x.png) | (2.32) |
Die Koeffizienten Bi heissen Virialkoeffizienten. Die Virialkoeffizienten Bi beschreiben die intermolekularen Kräfte und die Wirkung des Eigenvolumens der Teilchen. Je mehr Virialkoeffizienten berücksichtigt werden, desto genauer wird die Beschreibung des Zustandes des Gases.
Wir können die Virialkoeffizienten des van-der-Waals-Gases bestimmen, indem wir Gleichung (2.31) in eine Potenzreihe (Taylorreihe) entwickeln.
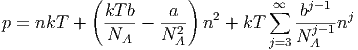 | (2.33) |
| Virialkoeffizient | ideales Gas | van-der-Waals-Gas | reales Gas |
| B2(T) | 0 | 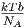 - -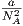 | B2(T) |
| B3(T) | 0 | kT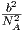 | B3(T) |
| B4(T) | 0 | kT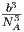 | B4(T) |
 |  |  |  |
| Bj(T) | 0 | kT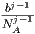 | Bj(T) |
 |  |  |  |
Der Virialkoeffizient B2(T) des van-der-Waals-Gases hängt von der Temperatur ab, die höheren Virialkoeffizienten nicht. Beim idealen gas sind alle Virialkoeffizienten identisch null.
Wir erhalten die erste Näherung der Zustandsfunktion eines realen Gases, wenn wir nur den Virialkoeffizienten B2(T) berücksichtigen.
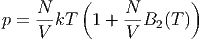 | (2.34) |
Da die langreichweitigen Kräfte zwischen den Molekülen attraktiv sind, ist der Druck des verdünnten realen Gases immer kleiner als der Druck des idealen Gases. Aus Gleichung (2.34) folgt dann sofort in der ersten Näherung, dass
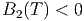 | (2.35) |
Bei sehr hoher Teilchendichte kommt der abstossende Teil der Wechselwirkungskräfte zum Tragen. Dann ist der Druck des realen Gases höher als der des idealen Gases. Wir haben also bei sehr hohen Drucken
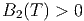 | (2.36) |
Da der Druck eines Gases erhöht werden kann, indem
man es aufheizt, muss B2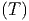 mit der Temperatur T
zunehmen.
mit der Temperatur T
zunehmen.
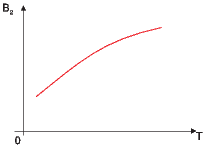
Temperaturverlauf des Virialkoeffizienten B2(T)
Wenn, was die Regel ist, 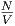 B2(T) « 1 kann
B2(T) « 1 kann 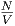 durch
durch
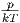 ersetzt werden (Annahme des idealen Gases). Wir
erhalten
ersetzt werden (Annahme des idealen Gases). Wir
erhalten
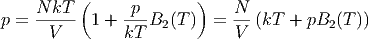 | (2.37) |
oder
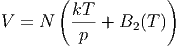 | (2.38) |
Damit können wir aus der ersten Näherung der Zustandsgleichung
des realen Gases den Joule-Thomson-Koeffizienten berechnen.
Aus der Definition von μ (Gleichung (2.23)) und aus der
Definition des Volumenausdehnungskoeffizienten α = 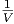
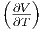 p
erhalten wir
p
erhalten wir
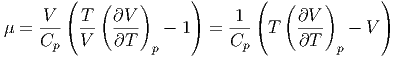 |
und damit
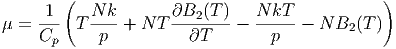 |
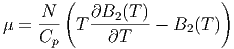 | (2.39) |
Da aber B2(T) mit der Temperatur zunimmt, ist auch
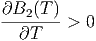 |
und damit
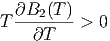 |
Bei tiefen Temperaturen, bei denen die Anziehungskräfte zwischen den Molekülen dominieren, ist B2(T) < 0. Dann ist aber μ > 0. Gase werden durch den Joule-Thomson-Effekt abgekühlt. Die Inversionskurve ist durch μ = 0 gegeben.
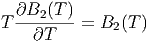 | (2.40) |
Die Inversionskurve beruht auf dem Wechselspiel von Anziehung der Moleküle bei tiefen Temperaturen und deren gegenseitiger Abstossung bei hohen Temperaturen.
 Lizenzinformationen
Lizenzinformationen