Weiter: Abbildungsverzeichnis Oben: Vorlesungsskript PHYS1100 Physik I Zurück: Berechnungen in ebenen schiefwinkligen Skript: PDF-Datei Übungen: Blätter
![[*]](crossref.gif) , Gleichung (3.45):
, Gleichung (3.45):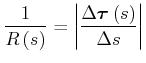
![[*]](crossref.gif) , Gleichung (3.46):
, Gleichung (3.46):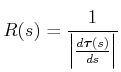
![[*]](crossref.gif) , Gleichung (3.19):
, Gleichung (3.19):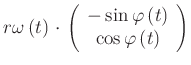 |
|||
![[*]](crossref.gif) , Gleichung (3.58):
, Gleichung (3.58):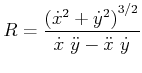
![[*]](crossref.gif) , Gleichung (3.80):
, Gleichung (3.80):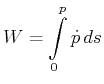
![[*]](crossref.gif) , Gleichung (3.87):
, Gleichung (3.87):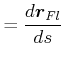 |
![[*]](crossref.gif) , Abschnitt D.2:
, Abschnitt D.2:

zwischen den Punkten ![]() und
und ![]() entlang der Bahn
entlang der Bahn ![]() . Wir nehmen an, dass die Bahn
. Wir nehmen an, dass die Bahn ![]() mit der
Bahnlänge
mit der
Bahnlänge ![]() parametrisiert sei. Dann ist
parametrisiert sei. Dann ist
![]() und der
Tangenteneinheitsvektor ist
und der
Tangenteneinheitsvektor ist

Mit
![]() und
und
![]() ist das Linienintegral
ist das Linienintegral
|
![[*]](crossref.gif) , Gleichung (3.68):
, Gleichung (3.68):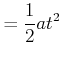 |
|||||||
![[*]](crossref.gif) , Abschnitt 3.2.6.3:
, Abschnitt 3.2.6.3:![[*]](crossref.gif) , Abschnitt 3.2.6.3:
, Abschnitt 3.2.6.3:![[*]](crossref.gif) , Gleichung (3.16):
, Gleichung (3.16):![[*]](crossref.gif) , Abschnitt F:
, Abschnitt F:![[*]](crossref.gif) , Gleichung (3.13):
, Gleichung (3.13):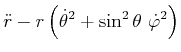 |
![[*]](crossref.gif) , Abschnitt 3.3.5:
, Abschnitt 3.3.5:![[*]](crossref.gif) , Abschnitt 3.3.5:
, Abschnitt 3.3.5:![[*]](crossref.gif) , Abschnitt 3.3.5:
, Abschnitt 3.3.5: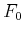 |
 |
||
 |
||
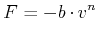 |
![[*]](crossref.gif) , Gleichung (3.126):
, Gleichung (3.126): |
||
 |
||
 |
||
 |
||
 |
![[*]](crossref.gif) , Gleichung (3.142):
, Gleichung (3.142):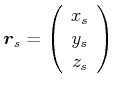
![[*]](crossref.gif) , Abschnitt 3.3.5:
, Abschnitt 3.3.5:![[*]](crossref.gif) , Abschnitt 3.4.2.1:
, Abschnitt 3.4.2.1: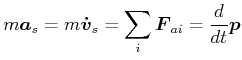
![[*]](crossref.gif) , Abschnitt 3.5.1.1:
, Abschnitt 3.5.1.1:![[*]](crossref.gif) , Gleichung (3.191):
, Gleichung (3.191):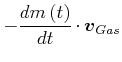 |
|||
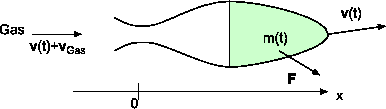 |
![[*]](crossref.gif) , Abschnitt 3.5.4.2:
, Abschnitt 3.5.4.2:![[*]](crossref.gif) , Gleichung (3.189):
, Gleichung (3.189):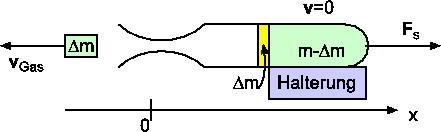
![[*]](crossref.gif) , Abschnitt 3.5.4.3:
, Abschnitt 3.5.4.3: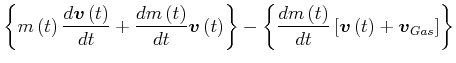 |
|||
![$\displaystyle \left\{ m\left( t\right) \frac{d\vec{v}\left( t\right) }{dt}+\fra...
...right) }{dt}\left[ \vec{v}\left( t\right) +\vec{v}_{Gas}\right]
\right\} \notag$](img1007.gif) |
|||
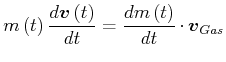 |
![[*]](crossref.gif) , Gleichung (3.197):
, Gleichung (3.197):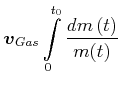 |
 |
||
![[*]](crossref.gif) , Abschnitt 3.6.4:
, Abschnitt 3.6.4:![[*]](crossref.gif) , Gleichung (3.218):
, Gleichung (3.218):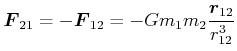
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2:![[*]](crossref.gif) , Abschnitt 3.7.2.1:
, Abschnitt 3.7.2.1: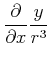 |
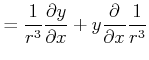 |
|
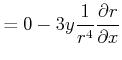 |
||
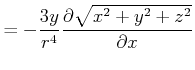 |
||
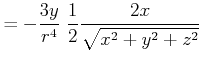 |
||
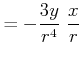 |
![[*]](crossref.gif) , Abbildung 3.56:
, Abbildung 3.56:![\includegraphics[width=0.71\textwidth]{mechanik-061.eps}](img1106.gif)
![[*]](crossref.gif) , Abschnitt 3.7.2.1:
, Abschnitt 3.7.2.1:Also haben wir
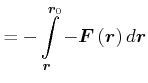 |
 |
|||
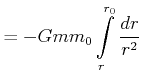 |
 |
|||
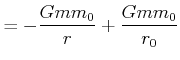 |
Es ist üblich, den Referenzpunkt
![]() zu setzen:
zu setzen:
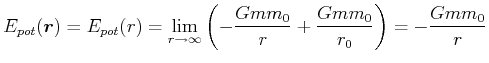 |
Damit ist die Behauptung gezeigt.
![[*]](crossref.gif) , Abschnitt 3.7.2.3:
, Abschnitt 3.7.2.3: , , |
![[*]](crossref.gif) , Abschnitt 3.7.2.3:
, Abschnitt 3.7.2.3:![[*]](crossref.gif) , Abschnitt 3.7.2.4:
, Abschnitt 3.7.2.4:![[*]](crossref.gif) , Gleichung (3.240):
, Gleichung (3.240):
![[*]](crossref.gif) , Gleichung (3.231):
, Gleichung (3.231):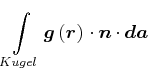 |
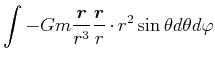 |
||
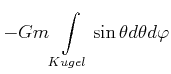 |
|||
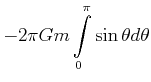 |
|||
![[*]](crossref.gif) , Abschnitt 4.2.3:
, Abschnitt 4.2.3:![[*]](crossref.gif) , Gleichung (4.18):
, Gleichung (4.18): |
||
 |
||
 |
||
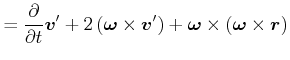 |
![[*]](crossref.gif) , Abschnitt 4.2.3:
, Abschnitt 4.2.3:![[*]](crossref.gif) , Abschnitt 4.2.3:
, Abschnitt 4.2.3:
ist, wobei ![]() die namens und
die namens und
![]() die namens ist.
die namens ist.
Wir haben also
Wir können die Gleichung für die vereinfachen, indem wir
![[*]](crossref.gif) , Abschnitt 4.2.4:
, Abschnitt 4.2.4:
Der Vektor ![]() hat die Länge
hat die Länge
Im gestrichenen Bezugssystem hat ![]() die Koordinaten
die Koordinaten
oder betragsmässig
Die Komponente parallel zum Boden (also in der ![]() -Richtung ist
-Richtung ist
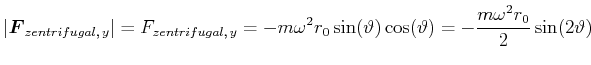 |
![[*]](crossref.gif) , Abschnitt 4.2.4.2:
, Abschnitt 4.2.4.2: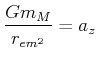
Weiter ist die Geschwindigkeit des Punktes ![]() bezogen auf die Geschwindigkeit
bezogen auf die Geschwindigkeit ![]() des Schwerpunktes
des Schwerpunktes ![]() gegeben
durch
gegeben
durch
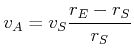
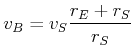
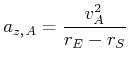
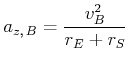
| Punkt |
Punkt |
|
| Feldvektor der Gravitation des Mondes |
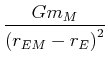
|
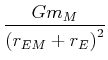
|
| Zentrifugalbeschleunigung |
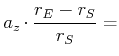
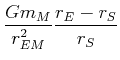
|
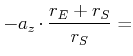
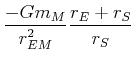
|
| Summe der Beschleunigungen |
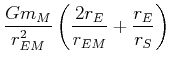
|
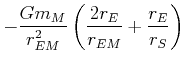
|
in ![]() gibt es die Zentrifugalbeschleunigung
gibt es die Zentrifugalbeschleunigung
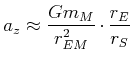
![[*]](crossref.gif) , Gleichung (4.19):
, Gleichung (4.19):![[*]](crossref.gif) , Abschnitt 4.3.1:
, Abschnitt 4.3.1:![[*]](crossref.gif) , Abschnitt 4.3.2.4:
, Abschnitt 4.3.2.4:
![\includegraphics[width=0.7\textwidth]{relativ-019.eps}](img1490.gif)
Die zwei Novae sollen an den angegebenen Orten und Zeiten ausbrechen. B
befindet sich in einem Inertialsystem, das sich mit der Geschwindigkeit
|
In der Abbildung stellt die horizontale Achse alle drei Raumkoordinaten zusammen dar. Am Ort ![]() befindet sich A
in Ruhe. Deshalb ist die Zeitachse von A sein hier. Andererseits haben alle Punkte auf der
befindet sich A
in Ruhe. Deshalb ist die Zeitachse von A sein hier. Andererseits haben alle Punkte auf der ![]() -Achse
die gleich Zeit wie A, sie befinden sich also jetzt. Die hier und jetzt
eines sich in einem mit der Geschwindigkeit
-Achse
die gleich Zeit wie A, sie befinden sich also jetzt. Die hier und jetzt
eines sich in einem mit der Geschwindigkeit ![]() gegenüber A's Inertialsystem bewegenden Beobachters B
sind gekippt gegenüber meinen Koordinatenachsen, wobei der Kippwinkel
gegenüber A's Inertialsystem bewegenden Beobachters B
sind gekippt gegenüber meinen Koordinatenachsen, wobei der Kippwinkel ![]() der Zeitachse (
der Zeitachse (![]() ,
hier) durch die Geschwindigkeit gegeben ist. Unbekannt ist der Kippwinkel
,
hier) durch die Geschwindigkeit gegeben ist. Unbekannt ist der Kippwinkel ![]() der Raumachse (
der Raumachse (![]() ,
jetzt). B soll gleichzeitig die Explosion von je einer Nova links und rechts von ihm beobachten. Beide Novae
sollen den gleichen Abstand von B haben. Sie sollen, als B's Weltlinie die von A kreuzte ausgebrochen sein
,
jetzt). B soll gleichzeitig die Explosion von je einer Nova links und rechts von ihm beobachten. Beide Novae
sollen den gleichen Abstand von B haben. Sie sollen, als B's Weltlinie die von A kreuzte ausgebrochen sein
Dies kann wie folgt eingesehen werden:
Zwischenbeobachtung: Die beiden roten Linien unter ![]() stellen die Ausbreitung des Lichtes dar, die
Lichtgeraden: die Lichtgeschwindigkeit bei unserer Wahl der Koordinaten ist 1. Die beiden
roten Linien durch die beiden Ereignisse zeigen, dass B beide Novae gleichzeitig wahrnimmt. A hingegen sieht
zuerst die Nova 1, dann die Nova 2, da der Schnittpunkt der ersten roten Linie mit der
stellen die Ausbreitung des Lichtes dar, die
Lichtgeraden: die Lichtgeschwindigkeit bei unserer Wahl der Koordinaten ist 1. Die beiden
roten Linien durch die beiden Ereignisse zeigen, dass B beide Novae gleichzeitig wahrnimmt. A hingegen sieht
zuerst die Nova 1, dann die Nova 2, da der Schnittpunkt der ersten roten Linie mit der ![]() -Achse unter dem der
zweiten Linie liegt.
-Achse unter dem der
zweiten Linie liegt.
| Der Begriff der Gleichzeitigkeit hängt vom betrachteten Inertialsystem ab. |
| Diagramme wie das us der Abbildung 4.18 heissen Minkowski-Diagramme. |
Je schneller ![]() ist, desto mehr werden, von
ist, desto mehr werden, von ![]() aus gesehen, seine Achsen gegen die
aus gesehen, seine Achsen gegen die ![]() Linie gekippt.
Linie gekippt.
![\includegraphics[width=0.7\textwidth]{relativ-020.eps}](img1510.gif)
Die beiden Novae aus der Sicht von B.
|
Die Beschreibung von B ist ebenso gültig. Aus seiner Sicht ist A's Geschwindigkeit genau das negative von
seiner, von A aus gesehen. Deshalb ist A's 'ct'-Achse um ![]() gegen den Uhrzeigersinn geneigt.
gegen den Uhrzeigersinn geneigt.
Ereignisse, die aus B's Sicht gleichzeitig sind, sind für A nicht gleichzeitig, und umgekehrt.
| Relationen zwischen Ereignissen sind nur dann sinnvoll zu beschreiben, wenn gleichzeitig auch das Bezugssystem angegeben wird. |
| In jedem Inertialsystem gibt es konsistente Masseinheiten, die aber von Inertialsystem zu Inertialsystem verschieden sind. |
![[*]](crossref.gif) , Gleichung (4.53):
, Gleichung (4.53):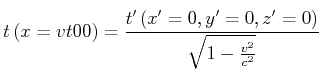
![[*]](crossref.gif) , Abschnitt 3.2.6.4:
, Abschnitt 3.2.6.4:
 |
||
 |
||
 |
||
![[*]](crossref.gif) , Abschnitt 4.3.5:
, Abschnitt 4.3.5:
![\includegraphics[width=0.99\textwidth]{relativ-025.eps}](img1549.gif)
Der longitudinale relativistische Dopplereffekt. Links
ist mein Standpunkt, rechts der von B.
|
Die obige Skizze soll die Frage klären, welche Periode ![]() B misst für ein Signal, für das ich die Periode
B misst für ein Signal, für das ich die Periode ![]() messe. Die Berechnung läuft wie folgt:
messe. Die Berechnung läuft wie folgt:
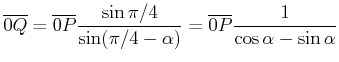
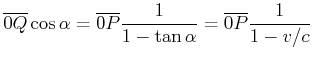
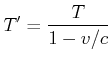
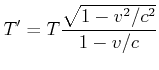
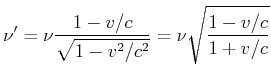
![]() würde anders argumentieren (rechte Seite von Abbildung 4.3.5)
würde anders argumentieren (rechte Seite von Abbildung 4.3.5)
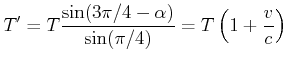
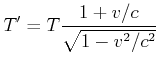
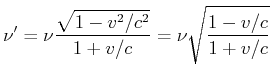
Der Dopplereffekt wird also durch die spezielle Relativitätstheorie für alle Inertialsysteme konsistent beschrieben.
Wenn eine Bewegung im Winkel ![]() schräg zur zur Beobachtungsrichtung verläuft, ist der relevante
Längenunterschied nicht
schräg zur zur Beobachtungsrichtung verläuft, ist der relevante
Längenunterschied nicht
![]() sondern
sondern
![]() . Sei
. Sei ![]() die Periodendauer im bewegten
Bezugssystem und
die Periodendauer im bewegten
Bezugssystem und
![]() die Distanz, um die sich das bewegte Bezugssystem in
die Distanz, um die sich das bewegte Bezugssystem in ![]() bewegt. Die
Zeitdilatation ist unabhängig von der Bewegungsrichtung, die Längenkontraktion jedoch nicht!
bewegt. Die
Zeitdilatation ist unabhängig von der Bewegungsrichtung, die Längenkontraktion jedoch nicht!
Wir erhalten die Beziehungen
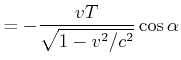 |
||
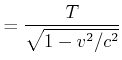 |
||
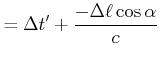 |
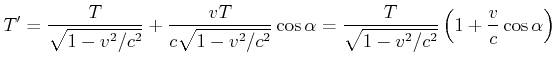
Für die Frequenzen (![]() ) gilt dann
) gilt dann
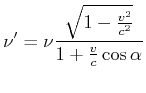 |
Für ![]() bekommt man den transversalen Dopplereffekt
bekommt man den transversalen Dopplereffekt
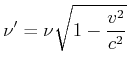 |
Dies ist nichts anderes als ein Ausdruck der Zeitdilatation. Bei Schallwellen gibt es keinen transversalen Dopplereffekt.
![[*]](crossref.gif) , Gleichung (4.87):
, Gleichung (4.87):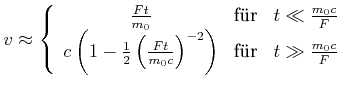
![[*]](crossref.gif) , Gleichung (4.88):
, Gleichung (4.88):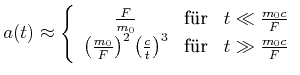
![[*]](crossref.gif) , Abschnitt 4.3.10:
, Abschnitt 4.3.10:![[*]](crossref.gif) , Abschnitt 5.1.4.1:
, Abschnitt 5.1.4.1:
![\includegraphics[width=0.9\textwidth]{starr-028.eps}](img1854.gif)
Wir betrachten die die
|
Dann ist
und
Die Drehungen um die ![]() folgt analog. Dann sind die Drehmatrizen gegeben durch
folgt analog. Dann sind die Drehmatrizen gegeben durch
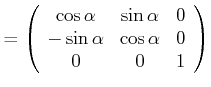 |
Drehung um |
||
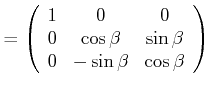 |
Drehung um |
||
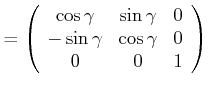 |
Drehung um |
Dann ist
wobei die Multiplikation von rechts durchzuführen ist. Das Resultat ist
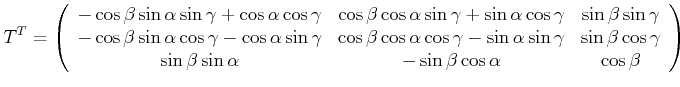 |
(H..930) |
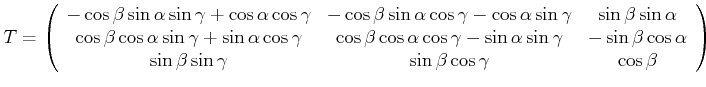 |
![[*]](crossref.gif) , Gleichung (5.10):
, Gleichung (5.10):![$\displaystyle \left( \begin{array}[c]{c} x y z \end{array} \right) =\left...
...array} \right) \left( \begin{array}[c]{c} x^* y^* z^* \end{array} \right)$](img1842.gif)
![[*]](crossref.gif) , Gleichung (5.12):
, Gleichung (5.12):![$\displaystyle T^{-1} = \left(\begin{array}[c]{ccc} R_{11} & R_{21} & R_{31} R_{12} & R_{22} & R_{32} R_{13} & R_{23} & R_{33} \end{array} \right)$](img1844.gif)
![[*]](crossref.gif) , Abschnitt 4.3.12:
, Abschnitt 4.3.12:![[*]](crossref.gif) , Abschnitt 4.3.6:
, Abschnitt 4.3.6:![[*]](crossref.gif) , Abschnitt 4.3.6:
, Abschnitt 4.3.6:![[*]](crossref.gif) , Abschnitt 4.3.7:
, Abschnitt 4.3.7: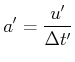
![[*]](crossref.gif) , Gleichung (5.31):
, Gleichung (5.31): |
||
 |
||
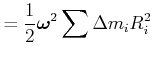 |
![[*]](crossref.gif) , Gleichung (5.28):
, Gleichung (5.28):![\begin{displaymath}\left(
\begin{array}[c]{c}
a_{2}b_{3}-a_{3}b_{2}\\
a_{3}b_{1}-a_{1}b_{3}\\
a_{1}b_{2}-a_{2}b_{1}
\end{array}\right)^2\end{displaymath}](img1945.gif) |
|||
![[*]](crossref.gif) , Abschnitt 4.3.10:
, Abschnitt 4.3.10:
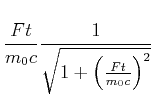 |
||
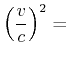 |
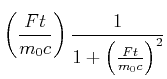 |
|
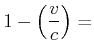 |
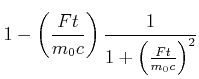 |
|
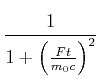 |
||
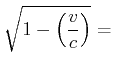 |
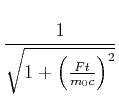 |
Mit
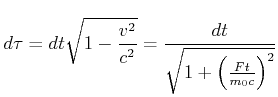 |
![[*]](crossref.gif) , Tabelle 5.1:
, Tabelle 5.1:|
|
![[*]](crossref.gif) , Abschnitt 4.3.11:
, Abschnitt 4.3.11:
![\includegraphics[width=0.4\textwidth]{relativ-029.eps}](img1725.gif)
Lorentztransformation als Drehung
|
Wir erproben, was wäre, wenn wir die Lorentz-Transformation als Drehung auffassen würden. Die ![]() -Achse würde
positiv (im Gegenuhrzeigersinn) um
-Achse würde
positiv (im Gegenuhrzeigersinn) um ![]() gedreht, die
gedreht, die ![]() -Achse würde negativ (im Uhrzeigersinn) um den
gleichen Winkel
-Achse würde negativ (im Uhrzeigersinn) um den
gleichen Winkel ![]() gedreht.
gedreht.
Wir verwenden die Definition
![]() sowie
sowie
![]() und
und
![]() .
.
Dann ist
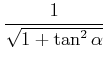 |
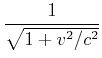 |
|||||
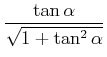 |
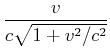 |
|||||
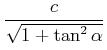 |
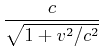 |
|||||
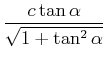 |
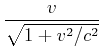 |
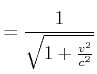 |
 |
|||||
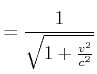 |
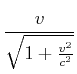 |
Eingesetzt, würde man eine Transformation erhalten, die formal wie die Lorentztransformation aussieht, die aber
unter der Wurzel ein ![]() -Zeichen anstelle des geforderten
-Zeichen anstelle des geforderten ![]() -Zeichens besitzt. Die Drehgleichungen wären dann
-Zeichens besitzt. Die Drehgleichungen wären dann
 |
|||||
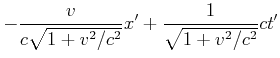 |
oder
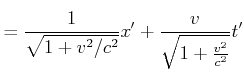 |
||
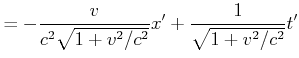 |
Diese Rotation sieht unserer Lorentz-Transformation sehr ähnlich. Die Vorzeichen unter den Wurzeln beim Cosinus
und beim Sinus sowie bei der Gleichung für ![]() stimmen nicht.
stimmen nicht.
Wenn man jedoch nicht ![]() als Zeitachse verwendet, sondern
als Zeitachse verwendet, sondern ![]() , wobei
, wobei
![]() die imaginäre Einheit ist,
bekommt man mit den obigen Drehgleichungen die Lorentz-Transformation. Dabei müssen alle Vorkommnisse von
die imaginäre Einheit ist,
bekommt man mit den obigen Drehgleichungen die Lorentz-Transformation. Dabei müssen alle Vorkommnisse von ![]() durch
durch ![]() ersetzt werden.
ersetzt werden.
Wir erhalten also
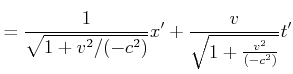 |
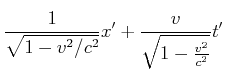 |
|||
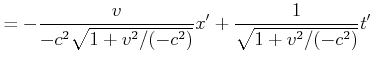 |
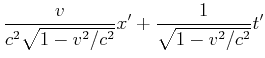 |
Der Vergleich mit Gleichung (4.98) zeigt, dass dies die Lorentztransformation ist. In einem Raum mit
den Koordinaten
![]() ist die Lorentz-Transformation nichts anderes als eine Rotation des
Koordinatensystems.
ist die Lorentz-Transformation nichts anderes als eine Rotation des
Koordinatensystems.
![[*]](crossref.gif) , Abschnitt 3.4:
, Abschnitt 3.4: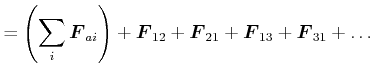 |
||
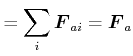 |
||
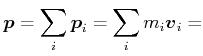 |
![[*]](crossref.gif) , Abschnitt 5.3.3:
, Abschnitt 5.3.3: |
||
 |
||
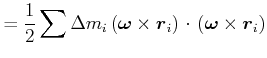 |
Wir verwenden das Spatprodukt
![]() und setzen
und setzen
![]() ,
,
![]() und
und
![]() . Dann ist
. Dann ist
![]() und damit
und damit
 |
||
 |
||
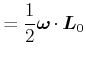 |
wobei wir die Definition des Drehimpulses
![]() verwendet haben.
verwendet haben.
![[*]](crossref.gif) , Gleichung (5.45):
, Gleichung (5.45): |
||
![[*]](crossref.gif) , Abschnitt 5.3.5.3:
, Abschnitt 5.3.5.3: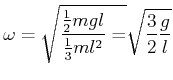 |
![[*]](crossref.gif) , Abschnitt 5.4.2.1:
, Abschnitt 5.4.2.1:
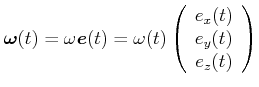 |
Durch Umstellen erhalten wir
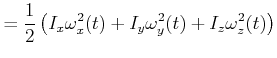 |
||
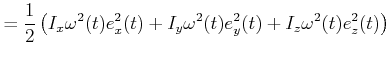 |
||
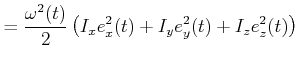 |
||
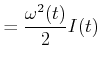 |
wobei wir
gesetzt haben. ![]() ist das Trägheitsmoment bezüglich der momentanen Drehachse
ist das Trägheitsmoment bezüglich der momentanen Drehachse ![]() .
Wenn die kinetische Energie des Kreisels erhalten ist, ist auch
.
Wenn die kinetische Energie des Kreisels erhalten ist, ist auch ![]() eine Konstante.
eine Konstante.
![[*]](crossref.gif) , Abschnitt 5.4.2.2:
, Abschnitt 5.4.2.2:![$\displaystyle \vec{u}=\left( \begin{array}[c]{c} u_{x} u_{y} u_{z} \end{a...
...ft( \frac{e_{x}}{\sqrt{I}},\frac{e_{y}}{\sqrt{I}},\frac{e_{z}}{\sqrt{I}}\right)$](img2196.gif) |
Wir setzen ![]() in die Ellipsengleichung ein und erhalten
in die Ellipsengleichung ein und erhalten
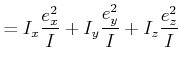 |
||||
 |
||||
 |
||||
![]() beschreibt also in der Tat die Oberfläche eines Ellipsoids, das wir Trägheitsellipsoid nennen. Aus der
Konstruktion folgen die Eigenschaften des Trägheitsellipsoides:
beschreibt also in der Tat die Oberfläche eines Ellipsoids, das wir Trägheitsellipsoid nennen. Aus der
Konstruktion folgen die Eigenschaften des Trägheitsellipsoides:
Aus Gleichung (5.88) folgt, dass die Längen der Halbachsen des Trägheitsellipsoides
![]() ,
,
![]() und
und
![]() sind.
sind.
Für einen allgemeinen Kreisel mit dem Fixpunkt 0 im Schwerpunkt ![]() gibt es die folgenden Beziehungen zwischen
den Hauptträgheitsmomenten:
gibt es die folgenden Beziehungen zwischen
den Hauptträgheitsmomenten:
![[*]](crossref.gif) , Gleichung (5.89):
, Gleichung (5.89):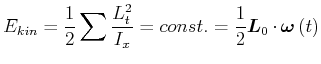
![[*]](crossref.gif) , Abschnitt 5.4.3.1:
, Abschnitt 5.4.3.1: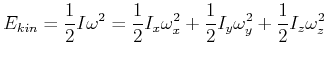
wenn
![]() die Kreisfrequenz im Hauptachsensystem ist. Da
die Kreisfrequenz im Hauptachsensystem ist. Da
![]() ist, sind alle einzelnen Komponenten kleiner als
ist, sind alle einzelnen Komponenten kleiner als ![]() . Also kann
man schreiben
. Also kann
man schreiben
![\includegraphics[width=0.4\textwidth]{starr-021.eps}](img2248.gif)
Poinsotsche Konstruktion
|
Die Zeichnung zeigt, dass damit auch
![]() und damit
und damit
![]() ist. Weiter ist nach Gleichung (5.83)
ist. Weiter ist nach Gleichung (5.83)
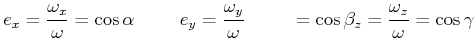
Nach Gleichung (5.86) ist
Wir setzen den Punkt ![]() im Abstand
im Abstand
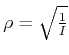 (siehe Gleichung (5.86) ) vom Nullpunkt auf die
Drehachse. Mit
(siehe Gleichung (5.86) ) vom Nullpunkt auf die
Drehachse. Mit
![$ Q=\left(
\begin{array}[c]{c}
x\\
y\\
z
\end{array}\right) =\vec{\rho}$](img3874.gif) wird
wird
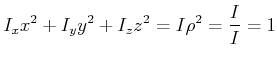 |
Diese Gleichung beschreibt also nichts anderes als das Trägheitsellipsoid.
Allgemein gilt, dass eine Funktion
![]() eine Oberfläche beschreibt. Dann ist der
Normalenvektor der Funktion
eine Oberfläche beschreibt. Dann ist der
Normalenvektor der Funktion
![]() ,
,![]() ,
,![]() durch
durch
Beweis:
Wir betrachten das totale Differential ![]() . Dieses muss null sein, da die Funktion
. Dieses muss null sein, da die Funktion
![]() eine Konstante
ist. Wir bekommen also
eine Konstante
ist. Wir bekommen also
 |
||
Damit ist
![]() senkrecht zu
senkrecht zu
![]() . Da
. Da
![]() in der Fläche
in der Fläche
![]() liegt (Die
möglichen Änderungen von
liegt (Die
möglichen Änderungen von
![]() sind durch die durch
sind durch die durch
![]() beschriebene Fläche begrenzt) ist
beschriebene Fläche begrenzt) ist
![]() senkrecht zur Tangentialebene und damit der Normalenvektor.
senkrecht zur Tangentialebene und damit der Normalenvektor.
|
Der Normalenvektor zum Trägheitsellipsoid
|
Im Hauptachsensystem ist
Von der Konstruktion her sind
![]() und
und
![]() parallel. Wir können wie folgt umformen
parallel. Wir können wie folgt umformen
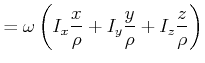 |
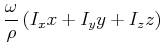 |
|||
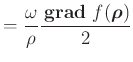 |
Deshalb ist
![]() , das heisst, dass
, das heisst, dass ![]() senkrecht zur Tangentialebene
senkrecht zur Tangentialebene
![]() im Durchstosspunkt
im Durchstosspunkt ![]() von
von
![]() durch das Trägheitsellipsoid ist.
durch das Trägheitsellipsoid ist.
![\includegraphics[width=0.4\textwidth]{starr-022.eps}](img2287.gif)
Trägheitsellipsoid
|
Rezept zur Konstruktion von ![]() :
:
| Voraussichtlich am 01.02.2006 |
![\includegraphics[width=0.4\textwidth]{starr-023.eps}](img2288.gif)
Interpretation der Poinsotschen Konstruktion
|
Wir bezeichnen mit ![]() den Abstand von 0 zur Tangentialebene
den Abstand von 0 zur Tangentialebene ![]() in
in ![]() . Der Abstand
. Der Abstand ![]() hat die
folgende Bedeutung
hat die
folgende Bedeutung
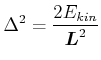 |
Beweis: Die Tangentialebene ![]() ist durch den Vektor
ist durch den Vektor
![]() ,
,![]() ,
,![]() gegeben. Dann gilt
gegeben. Dann gilt
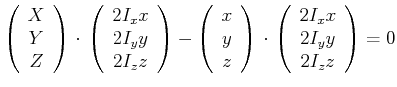
Ausmultipliziert erhält man
Wir bezeichnen mit
![]() den Einheitsvektor entlang
den Einheitsvektor entlang
![]() . Dann ist
. Dann ist ![]()
oder
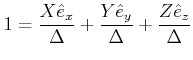 |
Wir vergleichen Gleichung (5.96) und Gleichung (5.98) . Die Vorfaktoren von ![]() ,
, ![]() und
und ![]() müssen identisch sein, da
bei beliebiger Variation der drei Grössen beide Gleichungen konstant sein müssen. Insbesondere kann man
müssen identisch sein, da
bei beliebiger Variation der drei Grössen beide Gleichungen konstant sein müssen. Insbesondere kann man ![]() setzen und bekommt dann
setzen und bekommt dann
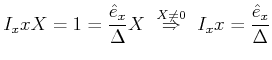
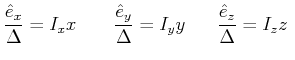 |
Da
![]() ein Einheitsvektor ist, gilt
ein Einheitsvektor ist, gilt
![]() und
und
![]() sind parallel, also ist
sind parallel, also ist
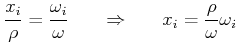 |
und
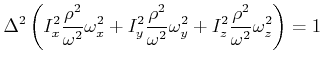 |
Mit der Definition
![]() bekommt man
bekommt man
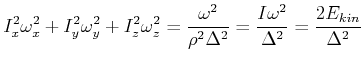 |
Andererseits ist
Damit folgt die Behauptung
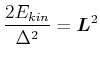 |
![\includegraphics[width=0.5\textwidth]{starr-024.eps}](img2313.gif)
Poinsot-Ellipsoid
|
Wir betrachten nun ein weiteres Ellipsoid, das Poinsot-Ellipsoid ![]() . Dieses ist ähnlich zum Trägheitsellipsoid
und liegt zu ihm konzentrisch. Wir wollen das Poinsot-Ellipsoid als Funktion von
. Dieses ist ähnlich zum Trägheitsellipsoid
und liegt zu ihm konzentrisch. Wir wollen das Poinsot-Ellipsoid als Funktion von
![]() darstellen. Die
Nutation im raumfesten Koordinatensystem wird nun beschrieben durch das Abrollen des Poinsot-Ellipsoids auf eine
Ebene
darstellen. Die
Nutation im raumfesten Koordinatensystem wird nun beschrieben durch das Abrollen des Poinsot-Ellipsoids auf eine
Ebene ![]() gegeben durch die Gesamtheit der Vektoren
gegeben durch die Gesamtheit der Vektoren
![]() . Diese Ebene
. Diese Ebene ![]() ist durch
ist durch
Am Berührungspunkt des Poinsotschen Ellipsoides muss die vorherige Gleichung auch stimmen. Deshalb ist die Ellipsengleichung im körperfesten Hauptachsensystem
 |
||
![$\displaystyle =\frac{1}{2E_{kin}}\left[ \left( I_{x}\omega_{px}\right) \omega _...
...ght) \omega_{py}+\left( I_{y}z\omega _{pz}\right) \omega_{pz}\right)] \nonumber$](img3878.gif) |
||
 |
||
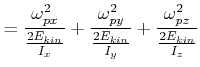 |
Die drei Halbachsen des Poinsotschen Ellipsoides ![]() sind
sind
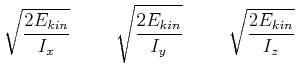
Der Punkt ![]() (Berührungspunkt zwischen dem Poinsot-Ellipsoid
(Berührungspunkt zwischen dem Poinsot-Ellipsoid ![]() und der Ebene
und der Ebene ![]() ) ist gegeben durch
) ist gegeben durch
Die Bahnkurve von ![]() auf
auf ![]() heisst Polhoide
heisst Polhoide
Die Bahnkurve von ![]() auf
auf ![]() heisst Herpolhoide
heisst Herpolhoide
Im körperfesten Hauptachsensystem ist der Winkelgeschwindigkeitsvektor
![]() die Verbindung zwischen
dem Fixpunkt 0 (beim freien Körper ist das der Schwerpunkt, beim Kreisel der Auflagepunkt) und der
Polhoide.
die Verbindung zwischen
dem Fixpunkt 0 (beim freien Körper ist das der Schwerpunkt, beim Kreisel der Auflagepunkt) und der
Polhoide.
Die Polhoide ist gegeben als Schnittpunkt des Poinsot-Ellipsoides ![]() und des Drallellipsoides
und des Drallellipsoides ![]() . Das
Drallellipsoid wird als Funktion der Variablen
. Das
Drallellipsoid wird als Funktion der Variablen
![]() ,
,![]() ,
,![]() geschrieben. Nach Gleichung (5.80) ist der Drehimpuls gegeben durch
geschrieben. Nach Gleichung (5.80) ist der Drehimpuls gegeben durch
Also können wir schreiben
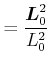 |
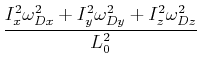 |
|||
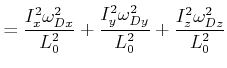 |
 |
Diese Gleichung definiert das Drallellipsoid ![]() . Das Drallellipsoid
. Das Drallellipsoid ![]() hat die Halbachsen
hat die Halbachsen
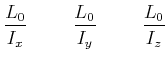
|
Bei einem reibungsfreien Kreisel ist sowohl seine kinetische Energie wie auch der Betrag seines
Drehimpulses erhalten. Die Winkelgeschwindigkeit
|
![[*]](crossref.gif) , Gleichung (5.113):
, Gleichung (5.113):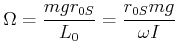
![[*]](crossref.gif) , Gleichung (5.114):
, Gleichung (5.114):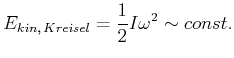
![[*]](crossref.gif) , Abschnitt 6.1.1.5:
, Abschnitt 6.1.1.5:
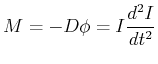 |
Daraus folgt für die Periodendauer
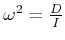 |
![[*]](crossref.gif) , Abschnitt 6.1.2.1:
, Abschnitt 6.1.2.1:| 0 | 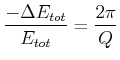 |
|||
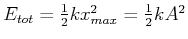 |
Dies ist eine quadratische Gleichung in ![]() Die Lösungen sind
Die Lösungen sind
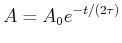 |
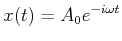 |
Es gibt drei Lösungen
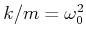 |
Bei
![]() haben wir bis jetzt nur eine Lösung. In den anderen
Fällen haben wir jeweils das
haben wir bis jetzt nur eine Lösung. In den anderen
Fällen haben wir jeweils das ![]() .
.
Die entsprechenden Lösungsfunktionen sind
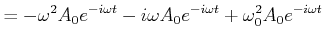 |
Wir testen noch, dass für
![]() die Lösung stimmt. Für diesen
Spezialfall lautet die Differentialgleichung
die Lösung stimmt. Für diesen
Spezialfall lautet die Differentialgleichung
| 0 |
Die Lösung der Schwingungsgleichung für den gedämpften Oszillator im Falle der unterkritischen Dämpfung ist
|
![[*]](crossref.gif) , Gleichung (6.69):
, Gleichung (6.69):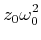 |
|||
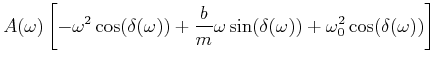 |
|||
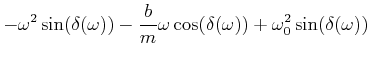 |
|||
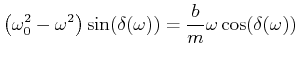 |
![[*]](crossref.gif) , Gleichung (6.70):
, Gleichung (6.70):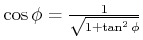 |
|||
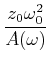 |
![[*]](crossref.gif) , Gleichung (6.73):
, Gleichung (6.73):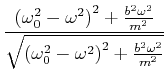 |
|||
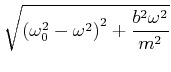 |
![[*]](crossref.gif) , Gleichung (6.75):
, Gleichung (6.75):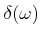
![[*]](crossref.gif) , Abschnitt 6.1.3:
, Abschnitt 6.1.3:
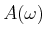 |
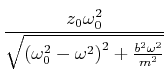 |
|||
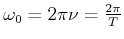 |
0 |
| 0 | 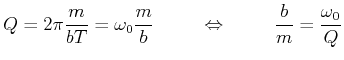 |
|
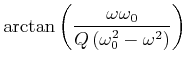 |
||
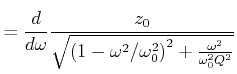 |
||
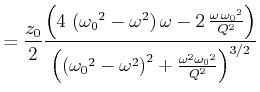 |
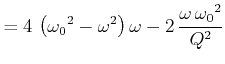 |
Diese Resonanzfrequenz) ist kleiner als die Eigenfrequenz eines ungedämpften Systems (Siehe Gleichung (6.58) ).
Die Bestimmung der Kenndaten eines Oszillators aus der Amplitude ist bei hohen
Güten ![]() sehr schwierig und sehr ungenau. Viel einfacher ist es, die Phase bei
sehr schwierig und sehr ungenau. Viel einfacher ist es, die Phase bei
![]() und ihre Steigung an der Stelle zu bestimmen.
und ihre Steigung an der Stelle zu bestimmen.
Berechnung der Steigung
![]() :
:
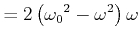 |
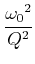 |
|
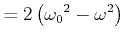 |
||
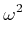 |
An der Stelle
![]() ist der Funktionswert
ist der Funktionswert
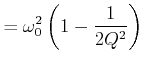 |
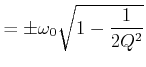 |
|||
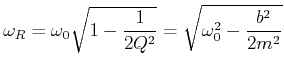 |
|
Bei der Resonanzfrequenz
Die Steigung der Phase
Es ist sehr viel einfacher, |
Othmar Marti