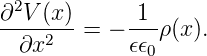

Ein elektrischer Kontakt zwischen zwei Medien besteht, wenn durch ihre Grenzfläche ein Ladungsträgertransport möglich ist. Im Folgenden betrachten wir einige, für die Halbleiter–Bauelemente relevante Beispiele:
Die Wirkungsweise der elektrischen Bauelemente beruht meist auf dem Ladungstransport durch Kontakte. Dieser ist praktisch ausschliesslich durch den ortsabhängigen Verlauf der potentiellen Energie der Ladungsträger in der unmittelbaren Umgebung der Grenzfläche festgelegt. Den sog. Potentialverlauf V (x) erhält man durch Divison der potentiellen Energie für Elektronen (bzw. für Löcher) mit −e bzw. (+e).
Ursache für diese Ortsabhängigkeiten sind Raumladungen, im Gegensatz zum Metall–Metall–Kontakt. Den formalen Zusammenhang zwischen dem elektrischen Potential, auch Makropotential genannt, und der gesamten elektrischen Ladungsträgerdichte ρ(x) liefert (für statische oder niederfrequente Betrachtungen) die Poisson–Gleichung der Elektrostatik:
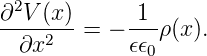 | (3.1) |
In dieser eindimensionalen Form ist sie Fixpunkt der folgenden quasiklassischen Beschreibung der allmählichen Bandverbiegung, deren auslösende Ursache ideale, auch abrupte Dotierwechsel sein können.
Einen Ausgangspunkt zur Erklärung eines Kontaktphänomens bietet das Bänderschema rund um die ebene Grenzfläche im thermodynamischen Gleichgewicht. Über den Kontakt hinweg ist die Fermi-Energie im ganzen Bauelement konstant; im Bandschema liegt sie also stets waagrecht. Der resultierende Strom von Ladungsträgern einer bestimmten Energie ist in jeder Raumrichtung gleich Null. (Erinnerung: Das chemische Potential, d. h. die Änderung der freien Energie mit der Teilchenzahl bei konstantem Volumen und konstanter Temperatur, ist gleich der Fermi–Grenzenergie.)
Denken wir uns einen Si–Kristall, der inhomogen dotiert wurde, in dem in der linken Hälfte Akzeptoren (B, Al, Ga) und in der rechten Donatoren (P, As, Sb) eingebracht wurden (siehe Dotierverfahren, später); zur Vereinfachung nehmen wir einen abrupten Wechsel der Störatomsorten an. Die Abbildung 3.16 gibt den Gang der Argumentation wieder.
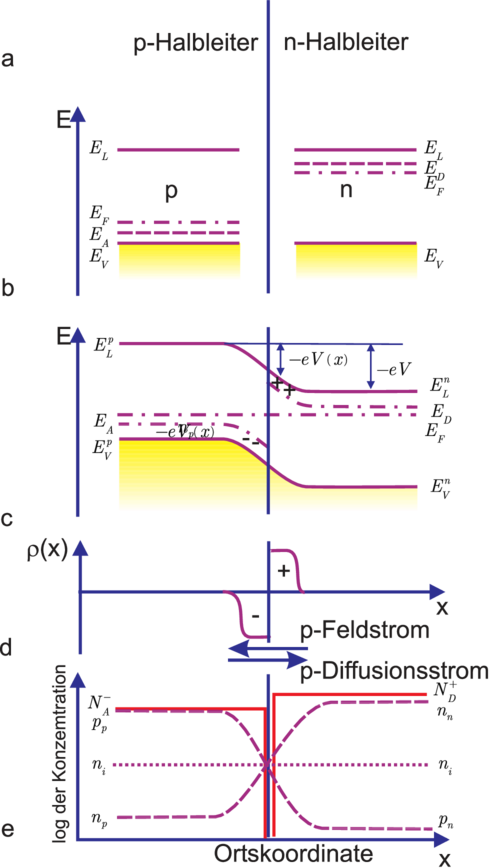
| Abbildung 3.16.: | Qualitatives Schema eines p–n–Übergangs im thermischen Gleichgewicht bei Raumtemperatur (gezeichnet nach Ibach-Lüth[IL99]). Beachten Sie bitte die logarithmische Auftragung! |
Zunächst denkt man sich die beiden Kristallhälften getrennt; die Fermi–Niveaus liegen in beiden Gebieten verschieden hoch bezogen auf dieselbe Energieskala. Für T ≈ 300K sind die Störstellen nahezu vollständig erschöpft, EF liegt entsprechend oberhalb von EA bzw. unterhalb von ED (b). Im nächsten Schritt setzt man die beiden Teile zusammen: im thermischen Gleichgewicht muss das Fermi–Niveau als elektrochemisches Potential (EF = EF′ + eU) gleich hoch und waagrecht sein. Im Übergangsbereich kommt es zu einer sog. Bandverbiegung, während ausserhalb die Ausgangslagen ungeändert erhalten bleiben (c). Die bereits eingeführte Poissongleichung Gleichung (3.1) verknüpft die Krümmung des Makropotentials mit einer Raumladung ρ(x), die über den sog. Raumladungsbereich oder die sog. Raumladungszone ausgedehnt ist (d). Im Falle der Störstellenerschöpfung sind links (fast) alle Akzeptoren geladen (NA−) und rechts ebenso (fast) alle Donatoren (ND+). Ausserhalb der Raumladungszone herrscht Ladungsträgerneutralität; links sorgen die positiven Löcher als Majoritätsladungsträger (pp) hierfür, rechts die negativen Elektronen als Majoritätsladungsträger (nn, sprich Elektronen (n) im n–Gebiet) (e). Die frei beweglichen Löcher und Elektronen diffundieren aufgrund des Konzentrationsgradienten ins angrenzende n– bzw. p–Gebiet. Dort sind sie Minoritätsladungsträger und ihre Konzentrationen werden als np (Elektronen im p–Gebiet) bzw. pn (Löcher im n–Gebiet) geschrieben; sie rekombinieren kräftig mit den vorhandenen Majoritätsladungsträgern. Folglich bleiben die Ladungen der ionisierten unbeweglichen Störstellen im Bereich der Raumladungszone unkompensiert; im p–Gebiet bleibt also eine negative, im n–Gebiet eine positive, ortsfeste Raumladung übrig. Dieses elektrische Feld der ‘inneren Diode’ ist Ursache für Feldströme, die den Diffusionsströmen der Löcher und Elektronen im thermischen Gleichgewicht entgegenfliessen und ihnen die Waage halten. (Aufgrund der endlichen Temperatur werden ständig und überall Elektron–Loch–Paare generiert und diese rekombinieren natürlich wieder.) Im thermischen Gleichgewicht gilt auch im Raumladungsbereich n·p = ni2.
Die sich einstellende Diffusionsspannung V D (maximale Differenz des elektrischen Potentials V (x)) hängt natürlich von den Dotierkonzentrationen ab:
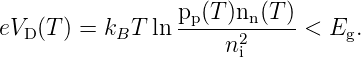 | (3.2) |
Die Leitungsbandkante ist dann ELp −eV (x) und die ortsabhängige Elektronenanzahldichte lässt sich (im Falle des nichtentarteten Halbleiters) angeben mit:
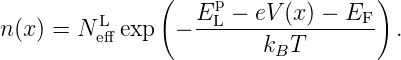 | (3.3) |
Die Berechnung des Verlaufs der Raumladungsdichte ρ(x) ist schwierig. Für den abrupten p–n–Übergang greift man daher zum ‘Schottky–Modell’ der Raumladungszone. In Abbildung 3.17 ist dies wiedergegeben.

| Abbildung 3.17.: | Das Schottky–Modell der Raumladungszone eines p–n–Übergangs (bei x = 0) (Zeichnung nach Ibach-Lüth[IL99]). |
Der unbekannte ρ(x)–Verlauf wird durch Kastenfunktionen angenähert. Die zugehörige Poissongleichung ist leicht lösbar, man erhält:
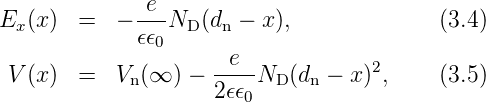
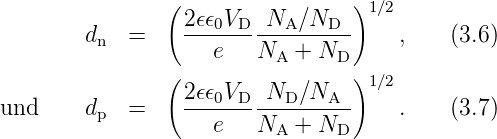
Bei Si und bei typischen Störstellenkonzentrationen von 1014 −1018cm−3 beträgt V D ≈ 0, 5 −0, 8V < Eg und es sind Ausdehnungen von dn bzw. dp von 1000 – 10 nm zu erwarten. Die Feldstärken in den Raumladungszonen liegen zwischen 104 und 106V∕cm, die Feldströme bzw. die kompensierten Diffusionsströme bei einigen kA∕mm2. Das sind beträchtliche Werte!
Dotiertechniken
Ein zentraler Schritt bei der Herstellung von p–n–Dioden ist
die Dotierung. Es gibt hierzu mehrere Fabrikationswege. Die
einfachste Art ist in Teilbild a) von Abbildung 3.18 gezeigt:
durch Erwärmen wird der feste, im direkten Kontakt stehende
Dotierstoff aufgeschmolzen und einlegiert. Definierter
sind die nächsten beiden Ofen–Diffusionsprozesse. Im
Teilbild b) wird nach der grossflächigen Diffusion (bei
800° − 1200°C) der Kontakt lateral durch einen Ätzprozess
festgelegt; es entsteht eine ‘Mesastruktur’. Im Teil c) dagegen
wird, wie heute allgemein üblich, durch eine Öffnung in
einer Oxidmaske eindiffundiert. Die seitliche Diffusion
unter die Oxidmaske ist allerdings unvermeidlich und
begrenzt die erzielbare laterale Auflösung. Im modernen
MOS–Prozess schliesslich kommt das letztgezeigte Verfahren
zum Einsatz. Mit Hilfe eines ‘Ionenimplanters’ werden bei
Beschleunigungsspannungen zwischen 50 und 300 keV
ionisierte Störatome implantiert. Sie sitzen auf Leerstellen
und in der Hauptsache auf Zwischengitterplätzen und
müssen in einem weiteren Ofenprozess bei ca. 900°C
erst noch auf Gitterplätze gebracht werden (‘elektrische
Aktivierung’).
Bei der Diffusion helfen einem mehrere glückliche Umstände. Erstens ist die Löslichkeit von As, B und P in Si grösser als die von z. B. Cu, Au oder O. Zum zweiten ist der Diffusionskoeffizient der gängigen Dotierstoffe gerade klein, d. h. ionenimplantierte Dotierprofile unter der Oberfläche überstehen den Aktivierungsprozess und nachfolgende, mit hohen Temperaturen verbundene Prozessschritte relativ unbeschadet.
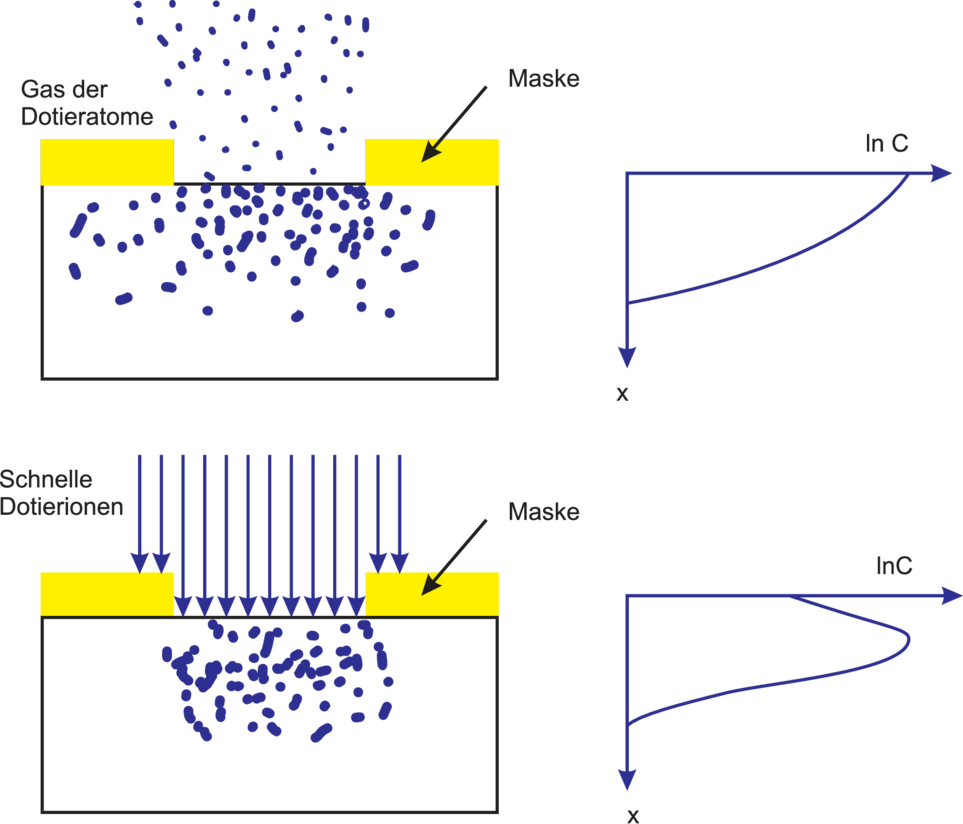
| Abbildung 3.19.: | Vergleich der Dotierprofile, die mit Hilfe eines Ofenprozesses (oben) und der Ionenimplantation hergestellt wurden, schematisch[Sze81]. |
Die Ofen–gestützen Dotierprozesse und die Ionenstrahl–gestützten
Dotiermethoden erzeugen unterschiedliche Dotierprofile
unter der Siliziumoberfläche, siehe Bild 3.19 Mehrere
Ionenimplantier–Prozessschritte mit unterschiedlichen
Beschleunigungsenergien ermöglichen die Anlage von in
der Tiefe gestaffelten, ausgedehnten oder modulierten
Dotierprofilen (vergl. CMOS–Herstellung).
Legt man eine zeitlich konstante, äussere Spannung U an einen p–n–Übergang, so erhält man einen stationären Zustand nahe am thermischen Gleichgewicht. Die Fermi–Energie als elektrochemisches Potential neigt sich jedoch nicht gleichmässig zur positiv vorgespannten Seite, sondern es fällt fast der gesamte Betrag von U über der Raumladungszone ab. Diese hat einen wesentlich höheren elektrischen Widerstand als die nebenliegenden Halbleiter–Gebiete. Der Grund liegt in der oben beschriebenen Rekombination von freien Löchern und freien Elektronen; die Raumladungszone ist gekennzeichnet durch eine Verarmung an freien Ladungsträgern (sog. Verarmungszone).
Über der Raumladungszone falle also jetzt statt der Diffusionsspannung der Wert
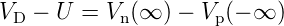 | (3.8) |
ab. Entsprechend dem Vorzeichen unterscheidet man zwei Fälle:
|
1. | 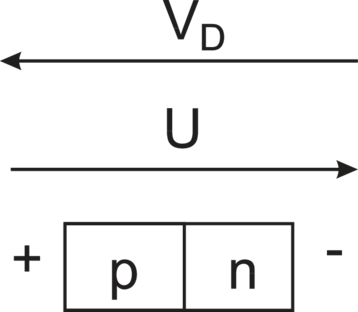 |
(p–Teil positiv gegen n–Teil): ‘Flussrichtung oder Durchlassrichtung’ Potentialhöhe: eV D −eU, die Diffusionsspannung wird erniedrigt. |
|
2. | 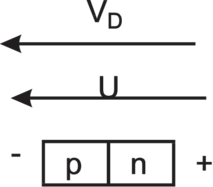 |
(p–Teil negativ gegen n–Teil): ‘Sperrrichtung” Potentialhöhe: eV D + eU, die Diffusionsspannung wird erhöht. |
Die Ausdehnung der Raumladungszone ändert sich: in Flussrichtungs–Polung wird sie schmaler, in Sperrrichtungs–Polung wird sie breiter. Aufgrund der Verarmung an freien Ladungsträgern hat dies direkte Folgen für die Leitfähigkeit der gesamten Anordnung, wir haben eine Diode.
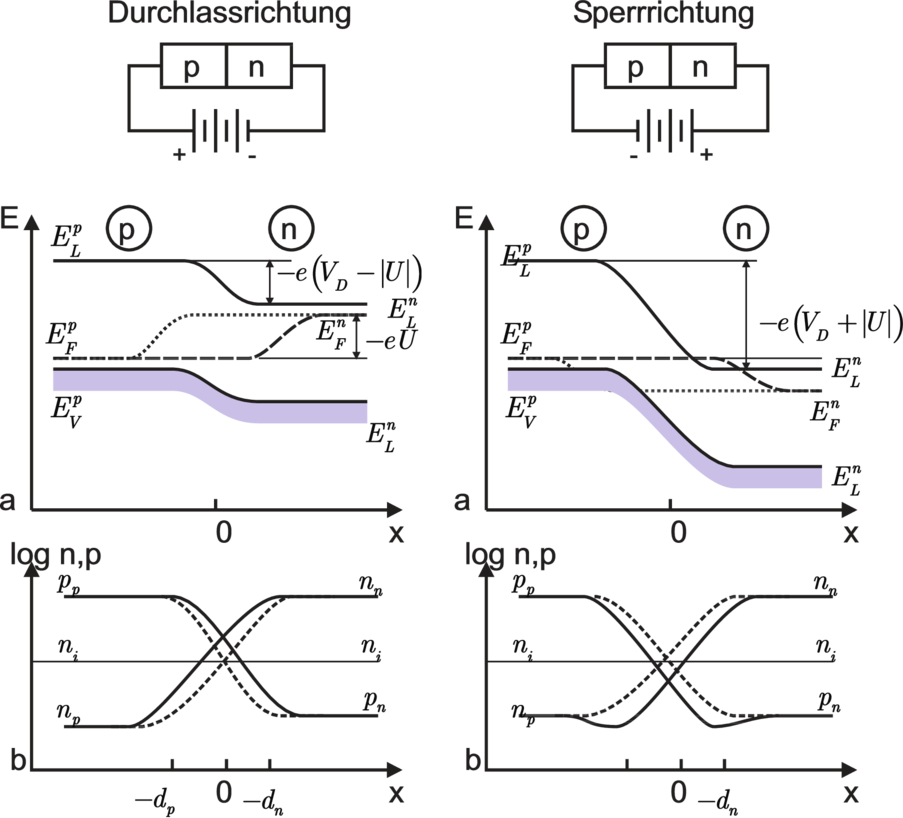
| Abbildung 3.20.: | Schema eines p–n–Übergangs, der in Durchlass– bzw. Sperrrichtung gepolt ist (Nichtgleichgewichtszustände) (gezeichnet nach [IL99]). |
Abbildung 3.20 gibt die Verhältnisse für den Fall des bereits eingeführten symmetrischen, abrupten p–n–Übergangs wieder. In Durchlassrichtung erniedrigt sich die Potentialhöhe. Um näherungsweise eine Beschreibung der Besetzung der Bänder mit Hilfe der Boltzmann–Statistik zu ermöglichen, werden satt des Fermi–Niveaus formal zwei sog. Quasi–Fermi–Niveaus für die Elektronen und für die Löcher eingeführt, obwohl strenggenommen kein thermisches Gleichgewicht mehr herrscht; das Massenwirkungsgesetz gilt in der Raumladungszone nicht mehr. (Das Fermi–Niveau liegt in der Mitte zwischen den Quasi–Fermi–Niveaus.)
Die Ladungsträgerdichten sind erhöht, ihre Ausläufer reichen diffusionsbedingt in die neutralen Gebiete. Die Elektronen laufen von rechts gegen die Potentialschwelle und ein Bruchteil überwindet diese gemäss dem Boltzmannfaktor
![[ ]
∼ exp −-e(VD-−--U)- .
kBT](phys_elektr643x.png)
Der Strom in Durchlassrichtung hängt also stark ab von der angelegten Spannung. Weil in Flussrichtung die Trägerdichten grösser sind als die Gleichgewichsdichten, überwiegt die Rekombination: der Ladungstransport erfolgt durch eindiffundieren von Elektronen und Löchern in die neutrale Zone und ihre dortige Rekombination: ‘Rekombinationsströme’.
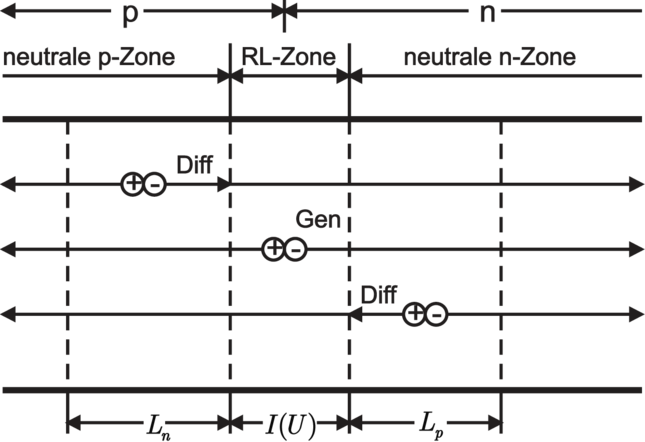
| Abbildung 3.21.: | Schematische Darstellung des Zustandekommens des Sperrstromes einer p–n–Diode mit Angabe des jeweils begrenzenden Mechanismuses(gezeichnet nach [Mül87]). |
In Sperrpolung ist es anders: die Trägerdichten in der Raumladungszone und in den naheliegenden neutralen Zonen sind unter den Gleichgewichtswerten; das System antwortet mit einer thermischen Netto–Generation von Ladungsträgern in diesem Bereich. Im elektrischen Feld der Raumladung werden Elektronen aus dem p–Gebiet ins n–Gebiet und Löcher aus dem n–Gebiet ins p–Gebiet (‘Feldströme der Minoritätsladungstäger’) gezogen. Diese ‘Generationsströme’ sind praktisch unabhängig von der Potentialhöhe und also unabhängig von der angelegten Spannung; sie sind proportional zu den entsprechenden Trägerdichten. Sie liefern den Sperrstrom der Diode.
Bildet man die Summe der Rekombinations– und Generationsströme von Löchern und Elektronen, so erhält man für die Kennlinie eines p–n–Übergangs (nur für die ‘innere Diode’, ohne Bahnwiderstände):
![( )
[ ( ) ]
I(U ) = ||Igen(n ) + Igen(p )|| exp -±eU--- − 1 .
(◟-------------p---------◝◜-------------------n---◞) mkBT
ISättigung](phys_elektr644x.png) | (3.9) |
Diese Gleichung beschreibt das Verhalten der Minoritätsladungsträger. Diese werden laufend am Rande der Verarmungszone gebildet. Der Vorfaktor ist materialabhängig.
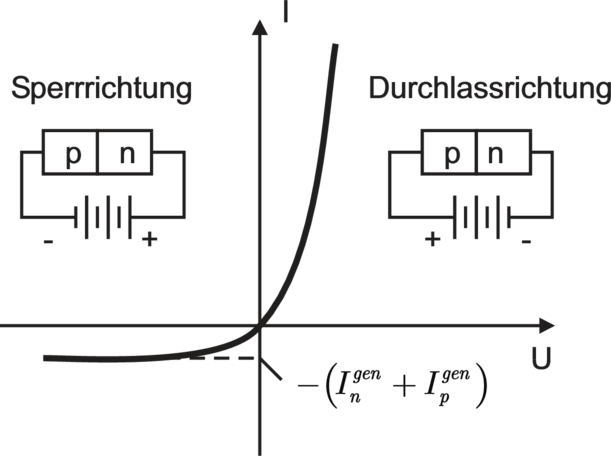
| Abbildung 3.22.: | Schema der Strom–Spannungs (I–U)–Kennlinie eines p–n–Übergangs(gezeichnet nach [IL99]). |
Dies ist die bekannte, extrem asymmetrische Gleichrichter–Kennlinie der Diode, wie sie im Bild unten gezeigt wird. m ist ein Korrekturfaktor (‘Idealitätsfaktor’).
Massgebend für diesen Kurvenverlauf ist also der Potentialverlauf am p–n–Übergang und der Rekombinations–/Generationsmechanismus.
Nebenbemerkung:
Die Berechnung von IS und m ist für Spezialfälle von
Shockley und Mitarbeitern durchgeführt worden. Für den
Fall der sog. Diffusionsstrom–Näherung bei geringer
Ladungsträgerinjektion lautet die Lösung:
![( )
eDp- eDn- [ (--eU---) ]
j(U ) = L pn + L np exp mk T − 1
p n B](phys_elektr645x.png) | (3.10) |
und beschreibt einen Kennlinienabschnitt im Durchlassbereich, vergleiche Bild 3.23. Diese Gleichung verknüpft alle in Kapitel 3.1.6 eingeführten Grössen in einfacher Weise.
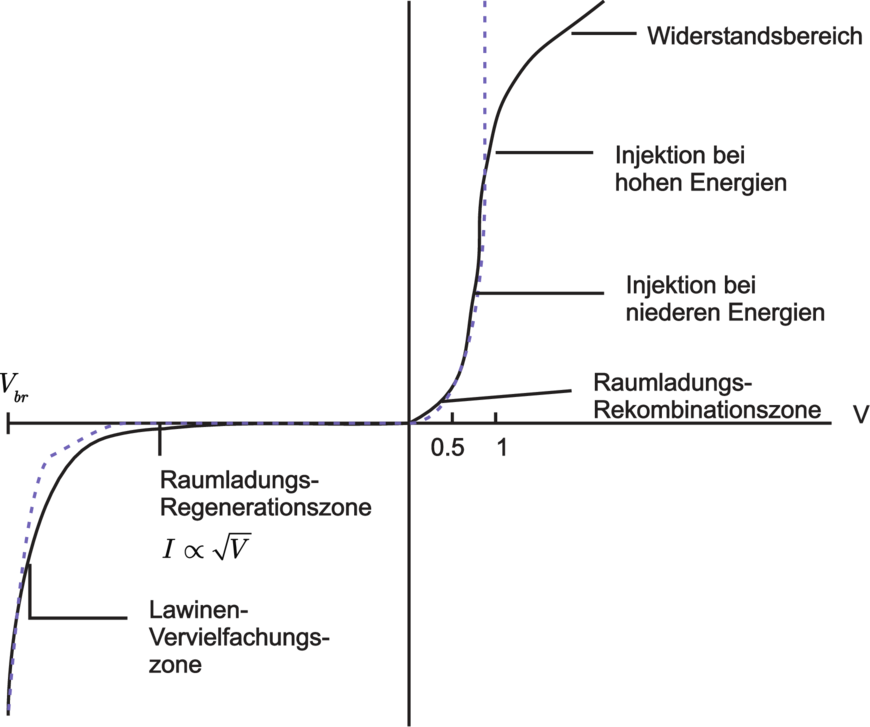
| Abbildung 3.23.: | I–U–Kennlinie einer p–n–Diode mit den Geltungsbereichen verschiedener Theorien bzw. Effekte (gezeichnet nach [Rou99]). |
Nicht mehr gültig ist die Kennlinienformel oberhalb der Durchbruchspannung; die Ursache hierzu kann eine im Feld der Raumladungszone ausgelöste Stossionisation sein (e− aus Valenzband ins Leitungsband), die sich lawinenartig vermehrt (‘Lawineneffekt’, ‘Lawinendurchbruch’, ‘Ladungsträgermultiplikation’) oder aber der sog. Zenereffekt, ein Tunneleffekt vom Valenzband im p–Teil zum Leitungsband im n–Teil. .
Nebenbemerkung:
Esaki–Dioden (sehr hoch und steil dotierte Dioden) zeigen
Tunneleffekte für beide Polungen. .
Nebenbemerkung:
Symmetrische abrupte p–n–Übergänge sind selten, meist
findet man asymmetrische Übergänge mit fertigungsbedingten
ausgeschmiertem Dotierprofil. Reale Kennlinien weichen
deshalb von der oben gezeigten Formel häufig ab. .
Abschliessend soll noch auf die kapazitive Wirkung der in der Raumladungszone gespeicherten Ladung hingewiesen werden. Mit dem Anlegen einer äusseren Spannung ändert sich die Zone, d. h. man transportiert Majoritäts– und Minoritätsladungsträger; im ersten Fall entspricht dies der sog. Sperrschichtkapazität, im zweiten Fall der sog. Diffusionskapazität.
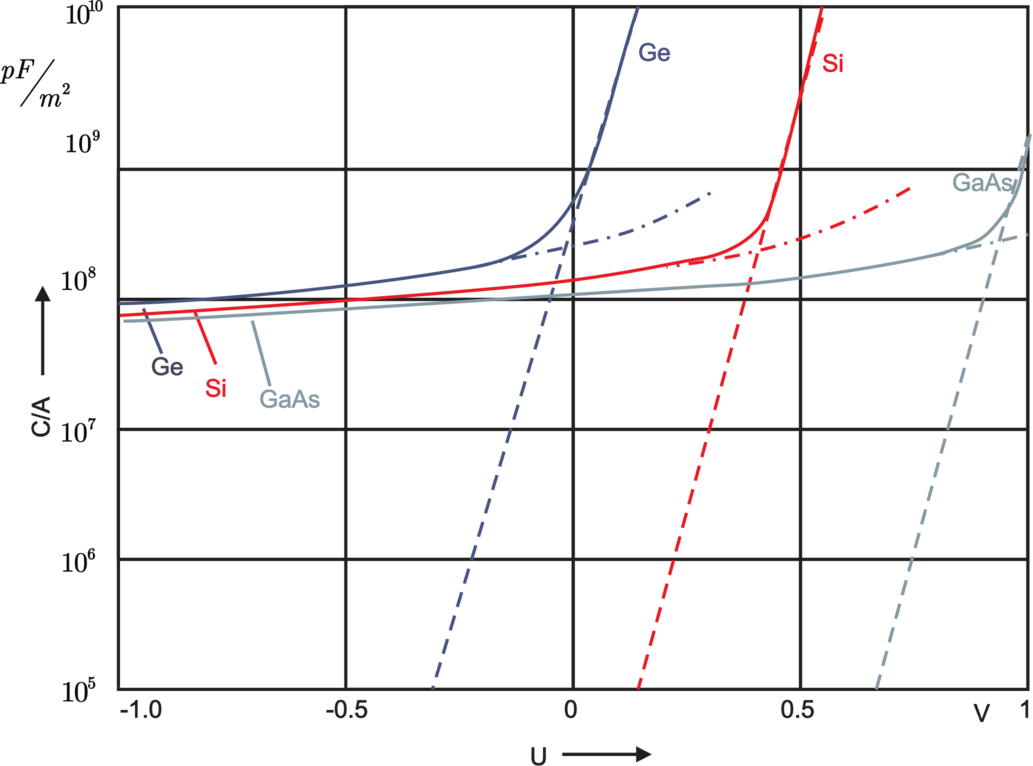
| Abbildung 3.24.: | Sperrschichtkapazität
(strichpunktiert), Diffusionskapazität (gestrichelt)
und Gesamtkapazität (voll ausgezogen) je
Flächeneinheit einer p+n–Diode als Funktion der
Diodenspannung U für Zimmertemperatur, berechnet für
(gezeichnet nach [Mül87]) |
Mit der Verfügbarkeit moderner Epitaxieverfahren wie der Molekularstrahlepitaxie und der Gasphasenepitaxie (MBE, molecular beam epitaxy, oder MOVCD, metal organic chemical vapour deposition)ist es möglich geworden, zwei verschiedene Halbleiter kristallin aufeinander aufzuwachsen. Zum Beispiel GaAs und AlAs oder, mit tolerablen Vorspannungen, SiGe auf Si. Mit der Variation der Zusammensetzung der Legierung (z. B. aus GaAlAs) kann man die Energielücke (z. B. zwischen 1, 4 −2, 2eV) gezielt einstellen. Die Übergänge können extrem scharf, d. h. auf atomarer Skala von Lage zu Lage wechselnd, hergestellt werden. (Schichtverfahren, siehe späteres Kapitel).
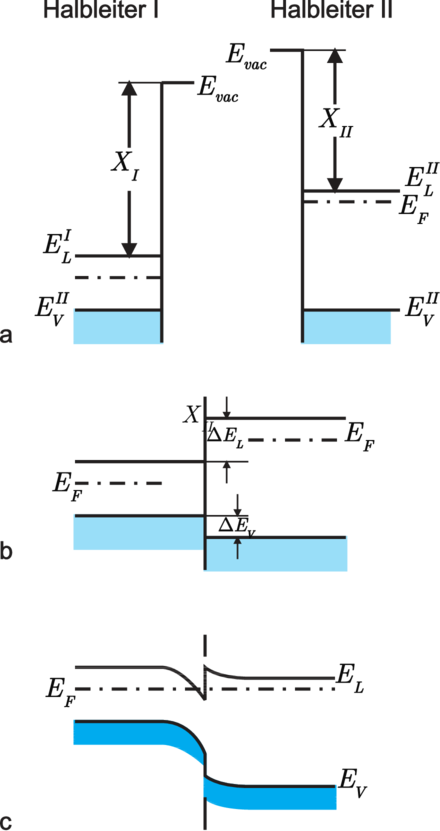
| Abbildung 3.25.: | Bänderschemata, die sich bei der Bildung einer Heterostruktur aus den Halbleitern I und II ergeben(gezeichnet nach [IL99]). |
Was geschieht nun, wenn man die beiden Halbleiter in Kontakt bringt? Es gibt zwei unterschiedliche Gesichtspunkte: erstens muss es aufgrund der unterschiedlichen Bandlückenbreiten sog. Banddiskontinuitäten ΔEV und ΔEL geben und zweitens wird es — genau wie beim p–n–Übergang in Si — eine Raumladungszone und also auch Bandverbiegungen geben, nur dass es hierfür mehr Möglichkeiten gibt (n–n, p–p, p–n, etc.).
Die Anpassung der beiden Bandstrukturen aneinander erfolgt von Atomlage zu Atomlage, die elektrischen Felder sind also in der Grössenordnung atomarer Felder (≳ 108V∕cm), sie sollten also die Banddiskontinuitäten festlegen. Das von Anderson stammende, in vielen Büchern zitierte Modell sieht dies auch so vor: die Bänderschemata der beiden Halbleiter sind so zusammenzusetzen, dass die Vakuum–Energieniveaus Evac (oder E∞) gleich sind. Für die Diskontinuität des Leitungsbandes ΔEL kann man aus Abbildung 3.25 direkt ablesen:
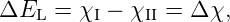 | (3.11) |
mit den Elektronenaffinitäten χi, den Differenzen zwischen
Evac und den unteren Leitungsbandkanten.
(Erinnerung: Das sog. Vakuumpotential ist die potentielle
Energie des Elektrons im Vakuum in unendlicher Entfernung
vom Kristallvolumen. Es gilt: χ = EL −E∞. Man könnte
auch die Austrittsarbeiten Φ = EF −E∞ zur Diskussion
heranziehen.)
Das Anderson–Modell liefert aber nicht die richtigen Werte, weil die bereits früher angesprochenen elektronischen Grenzflächenzustände lokal als Donatoren oder Akzeptoren zusätzlich wirksam sind. Wir folgen Ibach und Lüths[IL99] phänomenologischer Vorgehensweise und benützen für ΔEL bzw. ΔEV experimentell gefundene Werte. .
Die Bandverbiegungen erhalten wir auf dieselbe Weise wie bei der Si–Diode. Im thermischen Gleichgewicht sind die durch eventuelle Dotierungen festgelegten Fermi–Niveaus gleich; das bedingt einen Ladungstransfer, Rekombination und damit wieder die Ausbildung einer Raumladungszone. Wir erwarten wieder ausgedehnte Bandverbiegungen (typisch einige 10 nm) und Raumladungsstärken in der Grössenordnung 105V∕cm. Die einfachste theoretische Beschreibung erfolgt wieder mit dem Schottky–Modell, die verschiedenen Dielektrizitätskonstanten bewirken aber zwei verschiedene Diffusionsspannungen bzw. äussere Spannungen. In Bild 3.26 sind die Verhältnisse an einem sog. p–N–Heteroübergang wiedergegeben. Die negative Raumladung im p–Teil senkt die Bänder wieder zur Grenzschicht hin ab, die positive Raumladung im n–Teil rechts erhöht wieder die Potentiale. Die Diskontinuität ΔEV erscheint als senkrechtes Verbindungsstück in der Grenzfläche.
Hochinteressante physikalische Eigenschaften erhält
man bei sog. isotypen Heteroübergängen; diese sind
aus verschiedenen Halbleitern mit gleicher Dotierung
zusammengesetzt, also z. B. ein n–N–Übergang. Im n–Gebiet
der Raumladungszone entsteht eine Potentialtopf–artige
Anreicherungs–Raumladungszone mit lokal sehr stark
angehobener Elektronenkonzentration; dabei kann die
Dotierung im n–Gebiet fast intrinsisch sein, eine kräftige
Dotierung im N–Gebiet liefert ja die Ladungsträger. Die
zurückbleibenden ionisierten Donatoratome sind aufgrund
der räumlichen Trennung nicht mehr in der Lage, den
Elektronentransport in der Grenzfläche durch Streuung zu
schwächen. (Hohe Dotierung bedeutet normalerweise
hohe Streuung, hier nicht!) Diese einseitige Dotierung
wird ‘Modulationsdotierung’ genannt. Bringt man noch
eine ca. 10 nm dicke undotierte Schicht zwischen n–
und N–Gebiet, so vermeidet man die Streuprozesse von
lokalen Grenzflächenstörstellen zusätzlich. Auf diese Weise
werden extrem hohe Beweglichkeiten (> 106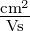 ) bei tiefen
Temperaturen erreicht.
) bei tiefen
Temperaturen erreicht.
Wächst man eine ganze Serie von solchen Schichtpaketen so auf, dass ein sog. Kompositionsgitter entsteht, so hat man eine ganze Reihe von Potentialtöpfen (sog. Quantentöpfen) zum parallelen Stromtransport zur Verfügung (siehe Abbildung 3.28). Zur Kontrolle des Wachstums verwendet man RHEED (Siehe Abschnitt 4.9.3.4).
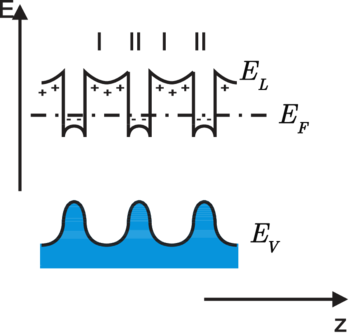
| Abbildung 3.28.: | Bänderschema eines modulationsdotierten Kompositions–Übergitters (gezeichnet nach [IL99]). |
Wenn die Schichtdicken genügend klein sind und damit die Quantentöpfe genügend eng (< 10nm), so treten in der Richtung senkrecht zur Schicht neue Quantisierungseffekte auf. Anschaulich: die Ladungsträger sind in einer Richtung eingesperrt, senkrecht dazu in der Kontaktebene sind sie frei beweglich.
Die theoretische Untersuchung löst i. allg. die zeitunabhängige Schrödingergleichung; im einfachsten Fall nimmt man in der relevanten Richtung ein unendlich hohes Rechteckpotential an, den Fall des isotropen Heteroübergangs löst man näherungsweise mit einem Dreieckspotential. Abbildung 3.29 zeigt die neuen Energieeigenwerte, die zugehörigen Subbänder und die konstante (!) Zustandsdichten der Subbänder. Für einen einzelnen Quantentopf erhält man scharfe Energiezustände. In Übergittern können aber die Abstände der Potentialtöpfe so klein sein (< 10nm), dass sich die Wellenfunktionen teilweise überlappen und man erhält wieder Bandaufspaltungen; je kleiner die Abstände, um so mehr ‘Subband–Aufspaltung’, siehe Photolumineszensspektroskopie.
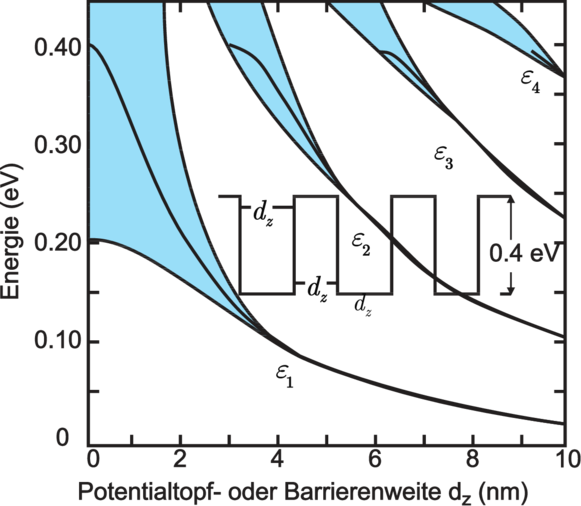
| Abbildung 3.29.: | Energiezustände von Elektronen, die in rechteckigen Potentialtöpfen des Leitungsbandes eines Kompositionsgitters ‘eingesperrt’ sind (gezeichnet nach [IL99]). |
Elektronische Bauelemente benötigen elektrische Zuleitungen mit geringen Verlusten. Also nimmt man ein Metall (meist Al bzw. genauer eine AlSiCu–Legierung, neuerdings Cu) und dampft oder sputtert es auf den Halbleiter. . Unter bestimmten Bedingungen erhält man so einen ohmschen Kontakt, oder aber das Gegenteil, nämlich eine Diode. Die Physik dazu hat vieles mit der bereits bei der p–n–Diode eingeführten gemeinsam.
Zu Beginn sei an die einfachen Verhältnisse des Metall–Metall–Kontakts erinnert (siehe Abbildung 3.30).
Das Bezugsniveau vor dem Kontakt sei wieder Evac (oder
E∞); die Fermi–Energie EFi (oder ζi′), die Austrittsarbeiten
Φi (oder Wi) und die Elektronenaffinitäten χi der beiden
Metalle seien ungleich. Im Kontakt müssen die beiden
Fermi–Niveaus gleich sein: es diffundieren vom Metall
mit der kleineren Austrittsarbeit mehr Elektronen zu
dem mit der grösseren Austrittsarbeit als umgekehrt
(Thermoemission), da die Ströme ∼ exp 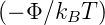 sind. In
der Grenzschicht bildet sich eine elektrische Doppelschicht
aus, Grenzflächenzustände spielen keine Rolle. Das Potential
ändert sich in der Grenzschicht, (aufgrund der vergleichsweise
sehr hohen Ladungsdichte der Metalle) nicht aber innerhalb
der Metalle. Es bildet sich also keine Raumladungszone aus,
Rekombination kann nicht auftreten. Man beobachtet das
sog. Kontaktpotential V K =
sind. In
der Grenzschicht bildet sich eine elektrische Doppelschicht
aus, Grenzflächenzustände spielen keine Rolle. Das Potential
ändert sich in der Grenzschicht, (aufgrund der vergleichsweise
sehr hohen Ladungsdichte der Metalle) nicht aber innerhalb
der Metalle. Es bildet sich also keine Raumladungszone aus,
Rekombination kann nicht auftreten. Man beobachtet das
sog. Kontaktpotential V K = 
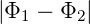 , eine direkt messbare
Potentialdifferenz (Messung mittels Kelvin–Methode);
der Sprung der Leitungsbandunterkanten eV G ist nicht
messbar (sog. Volta–Spannung). Die Ladungsträgerdichten
bleiben trotz des Ladungstransfers praktisch konstant. Es
gilt:
, eine direkt messbare
Potentialdifferenz (Messung mittels Kelvin–Methode);
der Sprung der Leitungsbandunterkanten eV G ist nicht
messbar (sog. Volta–Spannung). Die Ladungsträgerdichten
bleiben trotz des Ladungstransfers praktisch konstant. Es
gilt:
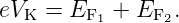 | (3.12) |
Komplizierter sind die Verhältnisse am Metall–Halbleiter–Kontakt. Betrachten wir zuerst den Kontakt zwischen Metall und n–Halbleiter.
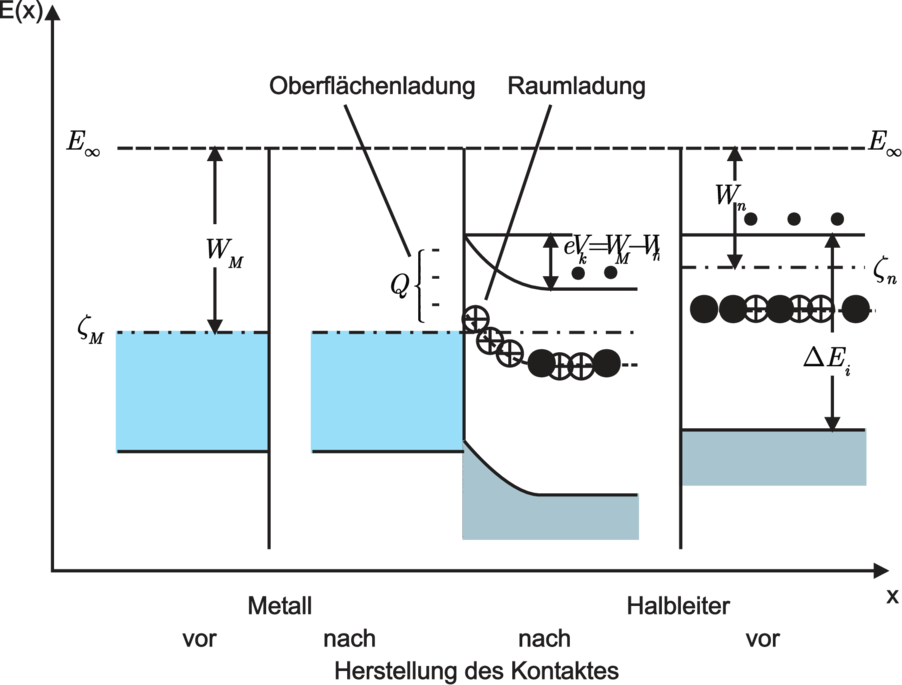
| Abbildung 3.31.: | Bänderschema eines Kontakts zwischen Metall und n–Halbleiter. (gezeichnet nach Weiss [Wei74]) |
Beschränkt man sich auf den Fall WM > Wn mit WM −Wn «Egap(ΔEi), braucht man nur das Leitungsband im n–Halbleiter mitzunehmen (sog. Einband–Modell). Wieder sorgt die Thermoemission für die negative Oberflächen–Ladung im Metall. Die positive Gegenladung im Halbleiter ist aber aufgrund der endlichen Anzahldichte ionisierbarer Donatoren ähnlich ausgedehnt wie bei der n–Zone des p–n–Übergangs: positive Raumladung durch ortsfeste (ionisierte) Donatoren.
Die Raumladungsdichte kann ganz analog zur theoretischen Beschreibung des p–n–Übergangs mit Hilfe der Poissongleichung benützt werden, um die sich einstellende Bandkrümmung auszurechnen. Die potentielle Zustandsenergie ist gegenüber EF erhöht, das Band krümmt sich in der Ladungszone nach oben, die Randschicht verarmt an Majoritätsladungsträgern.
Beim Kontakt zwischen Metall und p–Halbleiter mit WM < Wp und Wp −WM «Egap diffundieren Elektronen in den Halbleiter, rekombinieren mit Löchern und übrig bleibt die negative Ladung der ortsfesten, ionisierten Akzeptoren. Er zeigt eine Verarmungsschicht für Löcher, den Majoritätsladungsträgern im p–Halbleiter. Im Gegensatz zum p–n–Kontakt spielen hier die Minoritätsladungsträger beim Ladungstransport keine Rolle.
Die Verarmungszonen–Breite ist wieder abhängig von einer
aussen anlegbaren Spannung. Wir haben keinen ohmschen
Kontakt, sondern eine (dem p–n–Übergang sehr ähnliche)
Diode. Die thermische Beschreibung erfolgt wieder mit einem
kastenförmigen Raumladungsprofil, im Schottky–Modell.
Dies liefert einen parabelformigen Potentialverlauf, eine
Raumladungstiefe d ∼ND−1∕2 (Grössenordnung 10 nm und
mehr) und eine spannungsabhängige Kapazität C ∼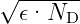 ,
die in der Halbleiter–Messtechnik zur Bestimmung der
Donatorkonzentration herangezogen wird.
,
die in der Halbleiter–Messtechnik zur Bestimmung der
Donatorkonzentration herangezogen wird.
Einen weiteren interessanten Fall erhalten wir, wenn |WM −WH|≈ ΔEi = Egap ist, wir also beide Bänder des Halbleiters und beide Ladungsträgerarten betrachten müssen (Zwei–Band–Modell). Die Elektronen, die ins Metall übergehen, können jetzt aus beiden Bändern stammen.
In diesem Fall erhalten wir im Leitungsband des Halbleiters eine Verarmung an Elektronen, aber im Valenzband eine Anreicherung an Defektelektronen (Löchern). Deshalb heisst dieser Randschichtbereich Inversionsschicht. Auf einem n–Halbleiter eignet sie sich zur Injektion von Löchern; auf einem p–Halbleiter (Anreicherung von Elektronen) zur Injektion von Elektronen (Fall hier nicht bildlich gezeigt). Injizierende Kontakte spielen für viele Bauelemente eine bedeutende Rolle.
Ein weiteres Beispiel für ein Zwei–Bänder–Modell ist der Kontakt von Metall und undotiertem Halbleiter. Aufgrund der geringen Ladungsträgerdichte wird die Raumladungszone extrem breit, z. B. bei Ge > μm. Soweit stimmen die gemachten Ausführungen mit einem Grossteil der Buchliteratur überein. Allerdings zeigen sich die Gleichrichterwirkung oder die Kapazität der Metall–Halbleiter–Kontakte im Experiment weitgehend unabhängig von einem gewählten Metall und seiner speziellen Austrittsarbeit. Ähnlich wie die in Kapitel 3.1.6 erwähnten Oberflächenzustände sind beim Metall–Halbleiter–Kontakt Grenzflächenzustände entscheidend für das Kontaktverhalten. Ist die von diesen ‘Zwischenzuständen’ verursachte Bandverbiegung grösser als die Differenz der Austrittsarbeiten, so ist der Einfluss des Metalls praktisch vernachlässigbar.
a)
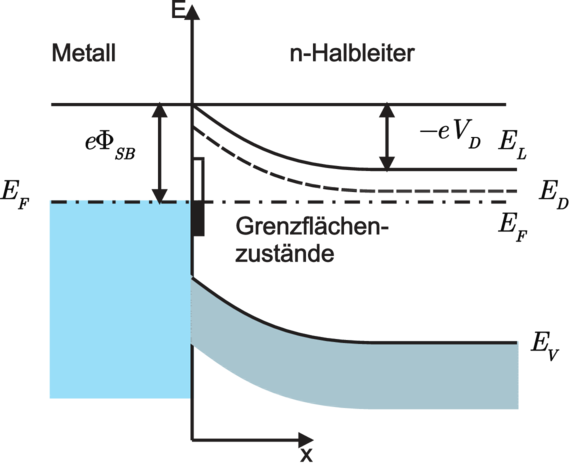

| Abbildung 3.34.: | Elektronisches Bänderschema eines Metall – n–Halbleiter–Übergangs mit Schottky–Barriere a) im thermischen Gleichgewicht, b) mit angelegter äusserer Spannung (gezeichnet nach [IL99]). |
Diese Oberflächenzustände wirken entweder als Donatoren oder Akzeptoren und sind entsprechend der Temperatur besetzt oder nicht, d. h. ihre Ladung wird durch die Lage des Fermi–Niveaus bestimmt; ihre Anzahldichte ist sehr gross (ca. 1014cm−2). Die Ladung der Grenzflächenzustände wird zur Herstellung der Ladungsneutralität durch die Ladung der ortsfesten ionisierten Donatoren kompensiert. Wir haben eine Verarmungszone, die zwar indirekt durch das die Grenzflächenzustände mitbestimmende Metall verursacht wird, die aber praktisch wenig mit der Austrittsarbeit des Metalls zu tun hat. Auch die Variation der Dotierung im Halbleiter ändert fast nichts an der Raumladung, ebensowenig das Anlegen einer äusseren Spannung. Die sog. Schottky–Barriere eΦSB ist deshalb eine für den speziellen Metall–Halbleiterübergang charakteristische Grösse, sie hängt allerdings etwas von präparativen Details ab.
Der reale Kontakt mit Verarmungsrandschicht zeigt eine Kennlinie der Form
![[ ±eU ]
j(U ) = jS· eβkBT-− 1 ,](phys_elektr653x.png) | (3.13) |
wobei β > 1 ist. In Durchlassrichtung ist die Verarmungsrandschicht verengt und die Potentialbarriere verringert; der Thermoemissionsstrom beträgt
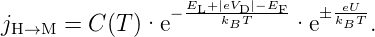 | (3.14) |
Der Sättigungsstrom ist fast unabhängig von der äusseren Spannung und lautet
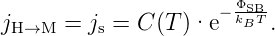 | (3.15) |
Zur hochohmigen Randschicht kommen noch der niederohmige
Bahnbeitrag des ‘Halbleiter–bulks’ hinzu.
In Abbildung 3.35 ist eine PtSi–n–Si–Diode im Aufbau
gezeigt.
Ohmsche Kontakte können auf mehrere Arten realisiert werden. Genannt wurde schon der Fall der Anreicherungsschicht (Inversionsschicht) beim injizierenden Kontakt; die Schicht ist niederohmiger als das Halbleiter–Volumen, die Bahnwiderstände dominieren; wir haben einen sog. sperrfreien Kontakt. Zwei weitere Möglichkeiten sind dadurch gegeben, dass man die Barriere durch Wahl eines besonders kleinen eΦSB sehr niedrig macht oder dadurch, dass man durch eine hochdotierte Schicht die Verarmungsschicht sehr dünn macht, so dass Elektronentunneln massiv möglich wird.
Reale ohmsche Kontakte stellt man auf p–Si her, so dass man Al direkt aufbringt und durch Ein–Legieren eine gute Haftung und eine p+–dotierte Zwischenschicht, also sehr gute Leitfähigkeit erhält. Dies funktioniert aber deshalb so gut, weil Al ein gutes Akzeptormaterial ist. Auf n–Si würde man so nur eine Umdotierung erreichen. Man scheidet deshalb ein ganzes Schichtpaket ab: Al–TiN–Ti–TiSi2–n–Si, wobei Ti als Diffusionsbarriere für das Al eingesetzt wird; der eigentliche Kontakt bildet wieder die Silizid–n–Si–Anordnung. Die Silizide (Ti, W, Mo, Pt, Ni) werden heute fast immer eingesetzt, da sie niederohmigere Kontakte als die elementaren Metalle erlauben.
Zum Abschluss des Kapitels werden die Eigenschaften von p–n– und Schottky–Dioden bildlich zusammengestellt.
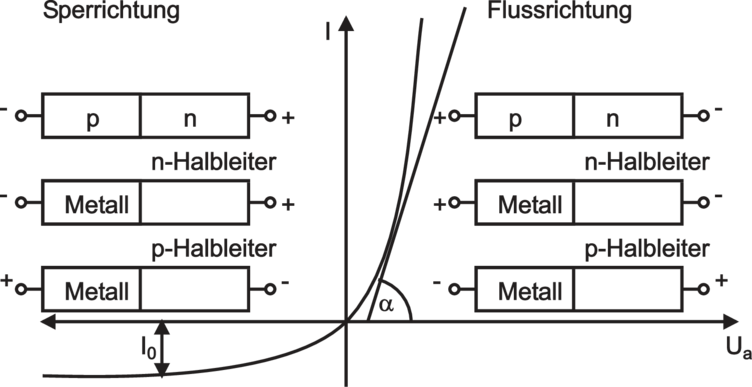
| Abbildung 3.37.: | Kennlinie eines gleichrichtenden Metall–Halbleiter–Kontaktes. (gezeichnet nach Hänsel/Neumann [HN96]) |
MIS (metal-isolator-semiconductor) –Kontakte sind ein extrem leistungsfähiger Grundbaustein in der Festkörperelektronik. Zum einen lassen sich damit Halbleiteroberflächen physikalisch untersuchen, zum anderen ist diese Anordnung in einer Vielzahl von Bauelementen enthalten, nämlich als Diode, als spannungsvariable Kapazität, als ‘charge–coupled device’ (CDD), als Transistor und schliesslich als das meistverbreiteste Element der Höchstintegration. Diese grosse technische Bedeutung erlangte der MIS–Kontakt in einer einzigen speziellen Zusammensetzung: MOS auf Si, das Oxid des Siliziums hat nämlich aufgrund seiner Herstellung durch thermische Oxidation ganz hervorragende Eigenschaften.
Man bringt eine sehr gut gereinigte Si–Oberfläche in einen Rohrofen und leitet O2–Gas ein. Der Sauerstoff reagiert an der Waferoberfläche mit dem Silizium und es bildet sich amorphes SiO2. Weiter angebotener Sauerstoff diffundiert durch die Oxidschicht und reagiert an der Grenzschicht. Durch die Massenzunahme wird die Waferoberfläche angehoben, knapp 45% der Oxiddicke liegen unter der ursprünglichen Oberfläche.
Bei der sog. trockenen Oxidation leitet man nur reinen Sauerstoff bei 1000°C - 1200°C ein; man erzeugt das ‘Gate–Oxid’ für MOS–Transistoren (< 100nm), die noch dünneren Tunneloxide stellt man bei ca. 800°C her. Die Gateoxid–Präparation ist der kritischste Schritt bei der Herstellung z. B. eines dynamischen RAM–Speichers. Bei der nassen Oxidation erhält man höhere Aufwachsraten, aber geringere Durchbruchfestigkeiten; so gewachsene Oxide werden als Feldoxide bezeichnet und häufig bei der Fertigung als Maskenmaterial eingesetzt. Ein spezielles Nassverfahren ist die sog. H2O2–Verbrennung; sie liefert sehr reine, allerdings weniger dichte Oxide, die bevorzugt als Kondensatordielektrikum in DRAM–Speichern eingesetzt werden. Die thermische Oxidation ist ein sehr langsamer Prozess mit Aufheiz– und Abkühlraten von ca. 1°C pro Minute, dabei können steile bzw. schmale Dotierprofile nicht stabil bleiben. Deshalb setzt man neuerdings RTP (rapid thermal processing) – Öfen für Einzelwafer mit Raten von 10 −100°C pro Minute ein. So lassen sich sehr dünne, dichte und glatte Oxide wachsen.
Den schematischen Aufbau einer MIS–Diode zeigt Abbildung 3.40. Eine äussere Spannung V sei positiv, wenn das Metall positiver als der ohmsche Kontakt des Halbleiters ist.
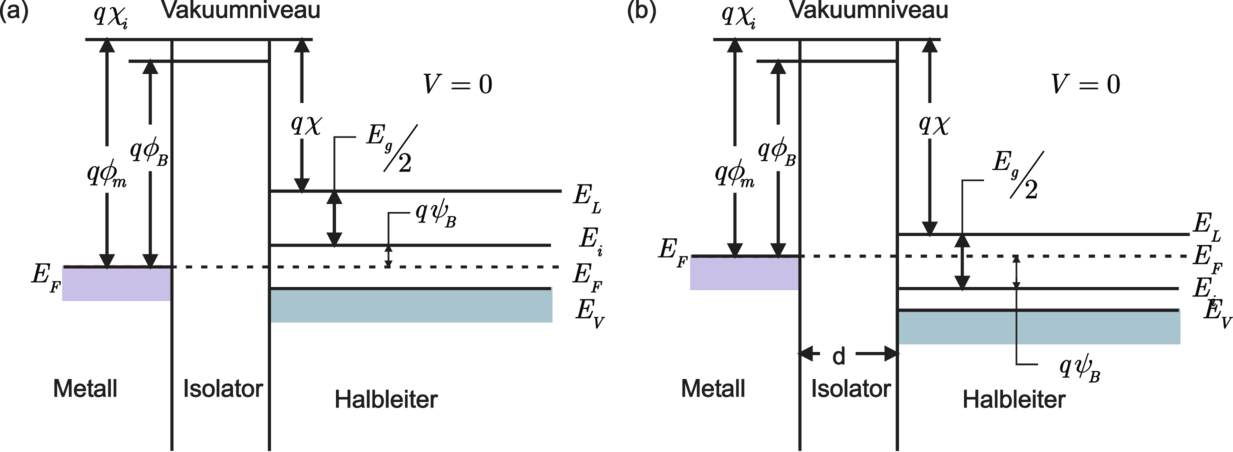
| Abbildung 3.41.: | Bänderschema einer idealen MIS–Diode: (a) mit p–Halbleiter; (b) mit n–Halbleiter (gezeichnet nach [Sze81]). |
Das Bändermodell einer idealen MIS–Diode bei V = 0 zeigt im thermodynamischen Gleichgewicht eine durchgängig waagrechte Fermi-Energie (‘flat-band condition’); die Differenz der Austrittsarbeiten von Metall und Halbleiter ist Null. Durch die Isolatorbarriere gibt es keinen Ladungstransport beim Anlegen einer Gleichspannung V . Die einzigen Ladungen, die unter V auftreten, sind dann im Metall an der Oberfläche und gleich gross mit entgegengesetztem Vorzeichen im Halbleiter. Im Halbleiter treten Phänomene auf, wie wir sie schon bei der idealen Schottky–Diode kennengelernt haben. Für negative Spannungen, also V < 0, erhalten wir im Falle des p–Halbleiters eine Anreicherungsschicht für die Majoritätsladungsträger, für positive Spannungen, also V > 0, erhält man eine Verarmungsschicht und für noch grössere positive V schliesslich einer Inversionsschicht: die Minoritätsladungsträgerdichte in der Raumladungszone ist grösser als die Majoritätsladungsträgerdichte. Die rechte Spalte in Abbildung 3.42 zeigt für den n–Halbleiter dieselben Effekte bei umgekehrter Spannungspolung. Die räumliche Ausdehnung der Bandverbiegung ist von derselben Grössenordnung wie bei den Beispielen im vorigen Kapitel (typisch 100nm).
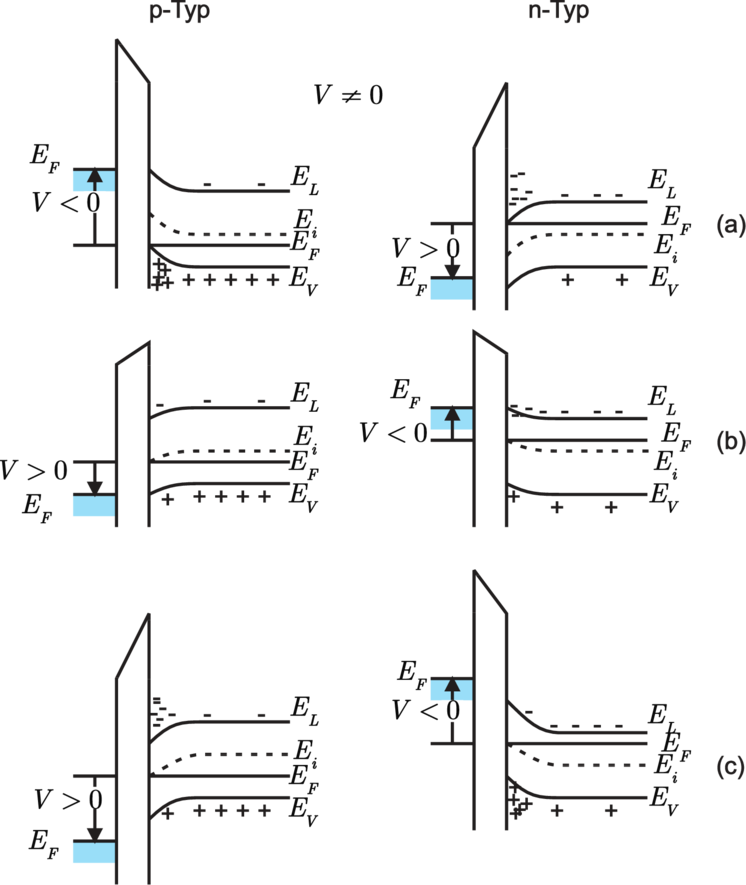
| Abbildung 3.42.: | Bänderschema einer idealen MIS–Dioden mit äusserer Spannung V (gezeichnet nach [Sze81]). |
Unter der Annahme, dass die Ladungsträgerdichten im
Volumen und an der Oberfläche jeweils exponentiell vom
Potential (∼ exp 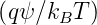 ) abhängen, lässt sich mit Hilfe der
Poissongleichung die Raumladungsdichte für eine bestimmte
Dotierkonzentration als Funktion des Oberflächenpotentials
(bezogen auf Eintrinsisch) berechnen.
) abhängen, lässt sich mit Hilfe der
Poissongleichung die Raumladungsdichte für eine bestimmte
Dotierkonzentration als Funktion des Oberflächenpotentials
(bezogen auf Eintrinsisch) berechnen.
Die angelegte Spannung fällt linear über der Isolatorschicht
und exponentiell in der Raumladungszone ab: V = V Isolator + ψS,
ψS=Oberflächenpotential. Analog ist die Gesamtkapazität der
MIS–Diode eine Reihenschaltung der Isolator–Kapazität
und der Verarmungsschicht-Kapazität im Halbleiter:
C = 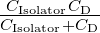 . CIsolator ist konstant und entspricht dem
Maximalwert des Systems, CD ist spannungs– und
frequenzabhängig.
. CIsolator ist konstant und entspricht dem
Maximalwert des Systems, CD ist spannungs– und
frequenzabhängig.
Die realen Verhältnisse in der Si–SiO2–MOS–Diode sind deutlich komplizierter als die ideale MIS–Diode es beschreibt. Abbildung 3.43 zeigt zum einen bewegliche Ladungen (Na+, K+) und getrappte Ladungen im SiO 2 und eine wenige nm tiefe, unvollständig oxidierte Zwischenschicht. Dazu ist die Tatsache zu bedenken, dass im amorphen Material immer unabgesättigte Bindungen vorhanden sind und dass es an den Kontaktflächen Metall–Isolator und Isolator–Halbleiter immer ionisierbare Grenzflächenzustände geben muss (‘interface trapped charge’), wobei letztere die Raumladung deutlich mitbestimmen (Erinnerung: Schottky–Diode).
Nebenbemerkung:
Durch einen Tempergang in H2–Atmosphäre bei ca. 450∘C kann
dieser Einfluss stark reduziert werden. Durch Aufwachsen des
Oxids unter Zugabe von Cl−–Ionen (HCl–Dampf oder
Trichlorethangas) können die beweglichen Ionen ortsfest
gebunden werden.
Die verbleibenden ortsfesten und getrappten Oxidladungen verändern das Bild von der Raumladung der idealen MIS–Diode, es shiften beispielsweise die flat–band–Bedingung, die C–V –Kurven und natürlich das Oberflächenpotential ψS. Die Differenz der Austrittsarbeiten ΦMS im thermodynamischen Gleichgewicht ist nicht mehr Null (Beispiel Al–SiO2–Si–Diode). In der Praxis gibt es aber für jede Dotierkonzentration im Si Materialien, die es im Falle V = 0 erlauben, eine Anreicherungs– oder Verarmungs–/Inversionsschicht gezielt zu realisieren.
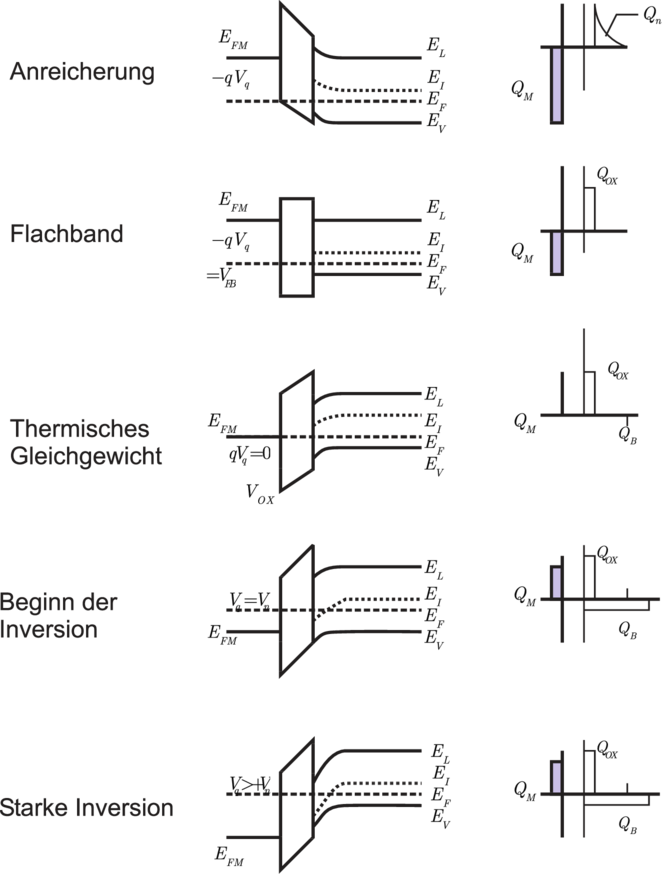
| Abbildung 3.44.: | Bänderschema und Raumladungen eines realen MOS–Kontaktes für verschiedene äussere Spannungen (p–Typ–Substrat), (vereinfacht gezeichnet nach [Rou99]). |
Für den Fall des p–Typ–Substrats seien im obigen Fall die wichtigsten Fälle vereinfacht im Bändermodell und in den Raumladungen zusammengefasst (siehe Abbildung 3.44). Für negative Spannungen erhält man den Fall der Anreicherung mit der Raumladungszone Qh der Löcher. Aufgrund der positiven Oberflächenladungen QOx benötigt die flat–band–Bedingung ebenfalls eine negative Vorspannung; ohne Vorspannung erhält man aus demselben Grund im thermodynamischen Gleichgewicht bereits eine Verarmung, d. h. die ausgedehnten Raumladungen der ionisierten Akzeptoren und schliesslich unten, wenn das Leitungsband so stark nach unten gekrümmt ist, dass es unter EF sinkt, kommt noch eine dünne Lage aus Elektronen (Minoritätsladungsträger, QE) im Falle der Invesion hinzu.
Äussere Einflüsse wie Temperatur, Licht, ionisierende Strahlung oder die Injektion heisser Ladungsträger beeinflussen das MOS—Dioden–Verhalten erheblich. Dem interessanten Fall, nämlich dem der Beleuchtung werden wir ein eigenes Kapitel widmen, nämlich der CCD im Kapitel 3.3.1.
Zum Abschluss dieses Kapitels sei noch auf das Problem der Segregation bei der thermischen Oxidation von dotiertem Si hingewiesen. Beim Tempern diffundieren die Störatome und wenn ihre Löslichkeit im SiO2 grösser ist als im Si selber, kommt es zu einer Absenkung der Dotierkonzentration im Si nahe dem Interface (‘pike–down’). Dies ist für den gebräuchlichsten Akzeptor Bor gerade der Fall. Der umgekehrte Fall (‘pike–up’) spielt in der Praxis keine grosse Rolle.
 Lizenzinformationen
Lizenzinformationen